3.1.1 勾股定理 课件(共42张PPT) 苏科版八年级数学上册
文档属性
| 名称 | 3.1.1 勾股定理 课件(共42张PPT) 苏科版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 19:53:46 | ||
图片预览










文档简介
(共42张PPT)
苏科版八年级数学上册
3.1.1勾股定理
讲课老师:
苏科版
八年级数学上册
一、复习回顾
在之前的学习中我们已经研究了一般的三角形的边和角的性质,本节课我们将继续研究特殊的三角形——直角三角形。
我们研究过直角三角形的性质,那么直角三角形的三边之间有着怎样的等量关系呢?我们从特殊的直角三角形——等腰直角三角形开始研究。
苏科版
八年级数学上册
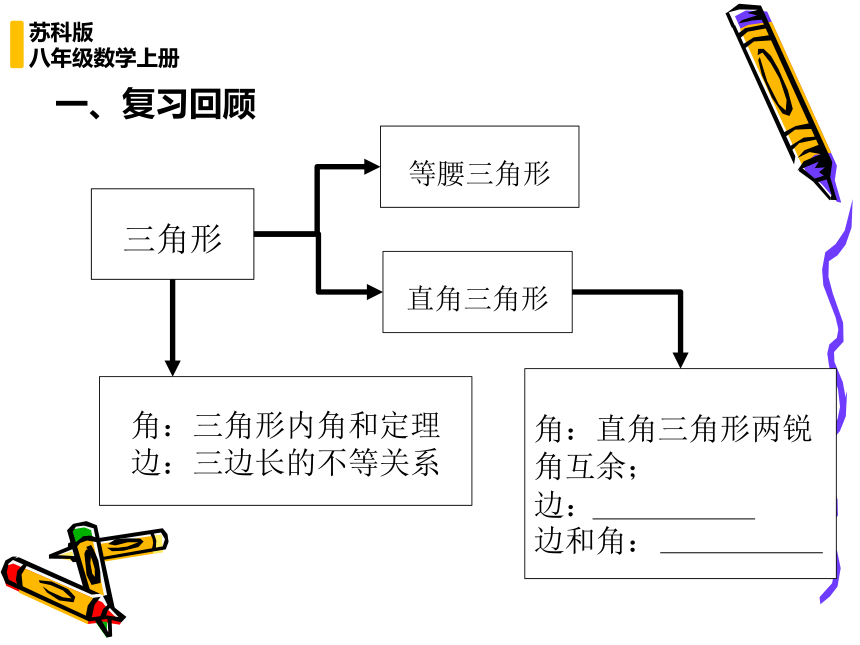
一、复习回顾
三角形
角:三角形内角和定理
边:三边长的不等关系
等腰三角形
直角三角形
角:直角三角形两锐角互余;
边:
边和角:
苏科版
八年级数学上册
二、课堂导入
相传在2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系。同学们我们来观察以下地面的图案,看看能从中发现什么数量关系?
问题1:
苏科版
八年级数学上册
二、课堂导入
在生活中是否仔细观察过建筑工人在建筑工地上的施工细节,建筑工人通常对于屋顶的倾斜角度和房间的对角线长度等这种比较难以实地测量的数据,一般会将它们放在一个直角三角形中去求,你们知道是为什么吗?
问题2:
苏科版
八年级数学上册
二、课堂导入
同学们,其实生活中有不少场景都有运用到今天即将所要学习的直角三角形勾股定理,例如,刚刚提到的测量屋顶的倾斜角度和房间的对角线长度等,这就是今天即将要学习的勾股定理的实际运用。通过这种联系,我们可以更好地理解数学知识的实际意义,数学其实与我们的实际生活密切相关。
苏科版
八年级数学上册
三、新知讲授
同学们还记得我们刚刚提到的毕达哥拉斯朋友家的地面图案嘛?我们现在来一起研究。
苏科版
八年级数学上册
三、新知讲授
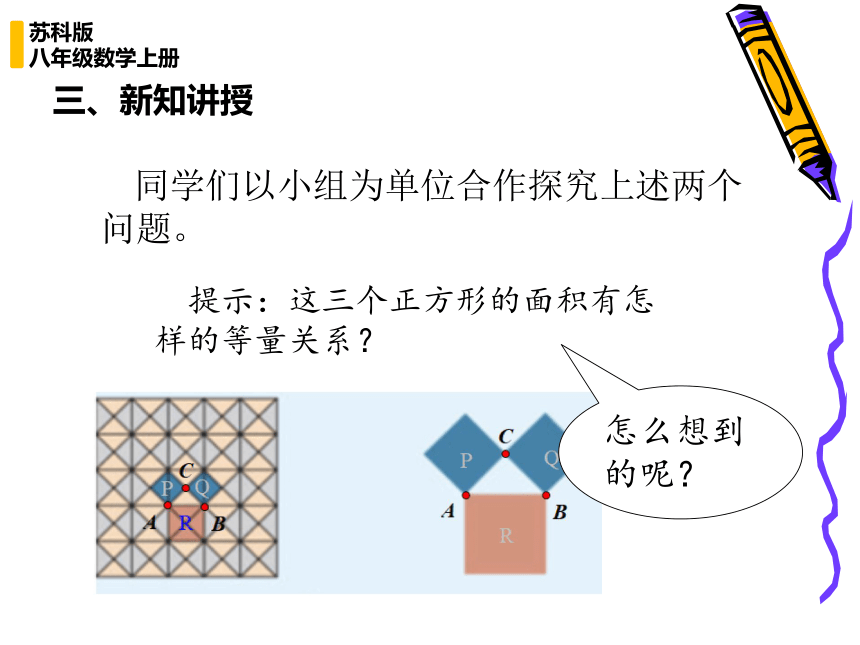
如图,在等腰三角形ABC中,∠C=90°,以AC为边作正方形P,以BC为边作正方形Q,以斜边AB为边作正方形R。请同学们以小组为单位思考,观察图形思考下列问题:
(1)三个正方形的面积之间有什么关系?
(2)等腰直角三角形ABC三边长度之间存在什么关系?
苏科版
八年级数学上册
三、新知讲授
同学们以小组为单位合作探究上述两个问题。
提示:这三个正方形的面积有怎样的等量关系?
怎么想到的呢?
苏科版
八年级数学上册
三、新知讲授
(1)以等腰直角三角形两直角边为边长的小正方形的面积和,等于以斜边为大正方形的面积;
(2)等腰直角三角形两直角边的平方和等于斜边的平方。
其实我们不难发现:
苏科版
八年级数学上册
三、新知讲授
同学们,这些平时看似平淡无奇的现象是不是有的时候却蕴含着深刻的道理呀!作为青少年的我们也要有一颗善于发现问题的眼睛,在生活中对于平时的现象要勤于思考,积极主动探索里面的奥秘,学会观察和记录生活中的细微变化,其实知识就在我们身边!
苏科版
八年级数学上册
三、新知讲授
既然等腰直角三角形的三边之间具有“两直角边的平方和等于斜边的平方”这一性质,那么一般的直角三角形是否也有这样的性质呢?
苏科版
八年级数学上册
三、新知讲授
请同学们试着表示出在下面网格中直角三角形三边衍生的正方形的面积之间的关系,看看三个正方形的面积有着怎样的等量关系。
苏科版
八年级数学上册
在计算正方形的面积时,学会使用“割”和“补”两种常见处理面积的方法来求正方形a的面积。
提示:
三、新知讲授
苏科版
八年级数学上册
请同学们拿出手中的方格纸,试着在方格纸中再画出几个一般形状的直角三角形,用类似于上面研究方法,小组合作一起探究一般性的直角三角形三边之间的等量关系。
三、新知讲授
苏科版
八年级数学上册
直角三角形三边衍生的正方形的面积之间的关系:
三、新知讲授
苏科版
八年级数学上册
请同学们对于一般性的直角三角形三边之间的等量关系进行合理适当的猜想。
命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么有
三、新知讲授
苏科版
八年级数学上册
对于上面提出的猜想,同学们是否能对其进行合理规范的证明呢?
三、新知讲授
苏科版
八年级数学上册
那接下来我们一起来了解一下我国古代第一位证明勾股定理的数学家——赵爽是如何证明的
三、新知讲授
苏科版
八年级数学上册
赵爽的主要贡献是约在222年深入研究了《周髀算经》,该书简明扼要地总结出中国古代勾股算术的深奥原理。其中一段530余字的“勾股圆方图”注文是数学史上极有价值的文献。他详细解释了《周髀算经》中勾股定理。
三、新知讲授
苏科版
八年级数学上册
赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,赵爽根据此图指出:四个全等的直角三角形(橙色)可以如图围成一个大正方形,中空的部分是一个小正方形(蓝色)。
三、新知讲授
苏科版
八年级数学上册
(1)一个小直角三角形的面积为 ;
(2)图1的面积为 ;
(3)图2的面积为 ;
(4)图1和图2的面积是否相等?你知道它们是通过何种变换得到的吗?
三、新知讲授
苏科版
八年级数学上册
下面我们通过视频动画来看看它们是怎么变换的:
三、新知讲授
苏科版
八年级数学上册
赵爽所用的这种方法是我国古代数学家常用的“出入相补法”。在西方,人们称勾股定理为毕达哥拉斯定理。因此“赵爽弦图”这个图案被选为2002年在北京召开的国际数学家大会的会徽。
三、新知讲授
苏科版
八年级数学上册
同学们我们古人赵爽利用“出入相补法”的原理证明出了勾股定理,体现了我国古代数学成就之高。纵观中国数学发展史,中国古代在数学方面的成就足以开一座陈列馆,体现出我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。所以我们要以我国优秀的民族文化感到骄傲。在这个信息多元的时代依然要保持对我们中华优秀传统文化的自豪感。
三、新知讲授
苏科版
八年级数学上册
古人赵爽的证明思想证实了命题1的正确性,命题1与直角三角形的边有关,我国把它称作勾股定理。
勾股定理 如果直角三角形的两直角边长分别为a和b,斜边长为c,那么
三、新知讲授
苏科版
八年级数学上册
在Rt△ABC中
∵∠C=90°
∴
符号语言:
三、新知讲授
苏科版
八年级数学上册
四、例题讲解
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a;
例1:设直角三角形的两条直角边长分别为a和b,斜边长为c:
苏科版
八年级数学上册
(1)已知a=6,c=10,求b;
例1:设直角三角形的两条直角边长分别为a和b,斜边长为c:
解:由勾股定理公式 ,已知a=6,c=10,代入公式得
四、例题讲解
苏科版
八年级数学上册
(2)已知a=5,b=12,求c;
例1:设直角三角形的两条直角边长分别为a和b,斜边长为c:
解:由勾股定理公式 ,已知a=5,b=12,代入公式得
四、例题讲解
苏科版
八年级数学上册
四、例题讲解
(3)已知c=25,b=15,求a;
例1:设直角三角形的两条直角边长分别为a和b,斜边长为c:
解:由勾股定理公式 ,已知c=25,b=15,代入公式得
苏科版
八年级数学上册
已知直角三角形的两个边的长度就可以根据勾股定理求出另外第三边的长度。此外,在一些没有明确长度是斜边长还是直角边的时候,要分类讨论。
四、例题讲解
苏科版
八年级数学上册
注意:同学们在平时做题时,要积累常见的勾股数,利于提高解题的速度。
常见的勾股数:
(3,4,5 ) 勾三股四弦五
(5,12,13 )
(6,8,10):连续的偶数
(8,15,17 )
它们的倍数也是勾股数!
四、例题讲解
苏科版
八年级数学上册
例2:如图,图中所有的三角形都是直角三角形,四边形都是正方形。已知正方形A,B,C,D的边长分别12,16,9,12,求最大正方形E的面积。
四、例题讲解
苏科版
八年级数学上册
解:由正方形A和B的边长为12和16,可知正方形A的面积
正方形B的面积
同理:由正方形C和D的边长为9和12,可知正方形C的面积
正方形D的面积
四、例题讲解
苏科版
八年级数学上册
最后:勾股定理探究过程可得,两个中等的正方形面积分别为400和225;由此得出最大正方形E的面积为400+225=625.
总结:在充分理解勾股定理探究过程的基础上,掌握直角三角形三边衍生出的正方形的数量关系。
四、例题讲解
苏科版
八年级数学上册
课本p28的练习1-3题
五、课堂练习
苏科版
八年级数学上册
本节课你学了哪些内容:
1.在探究直角三角形三边关系时,得到有关三边延申出的正方形面积的等量关系是什么?
直角三角形三边衍生的正方形的面积之间的关系:
六、课堂小结
苏科版
八年级数学上册
本节课你学了哪些内容:
2.勾股定理的内容是什么?几何语言怎么表示?
勾股定理 如果直角三角形的两直角边长分别为a和b,斜边长为c,那么
在Rt△ABC中
∵∠C=90°
∴
几何语言:
六、课堂小结
苏科版
八年级数学上册
六、课堂小结
本节课你学了哪些内容:
3.能说说“赵爽弦图”是如何证明勾股定理的吗?
利用旋转前后的面积相等
苏科版
八年级数学上册
七、课后作业
1.必做题:教材课后的练习题;查阅相关资料和书籍了解其他的有关勾股定理的证明;
2.选做题:练习册B组;
苏科版
八年级数学上册
再见!
苏科版
八年级数学上册
苏科版八年级数学上册
3.1.1勾股定理
讲课老师:
苏科版
八年级数学上册
一、复习回顾
在之前的学习中我们已经研究了一般的三角形的边和角的性质,本节课我们将继续研究特殊的三角形——直角三角形。
我们研究过直角三角形的性质,那么直角三角形的三边之间有着怎样的等量关系呢?我们从特殊的直角三角形——等腰直角三角形开始研究。
苏科版
八年级数学上册
一、复习回顾
三角形
角:三角形内角和定理
边:三边长的不等关系
等腰三角形
直角三角形
角:直角三角形两锐角互余;
边:
边和角:
苏科版
八年级数学上册
二、课堂导入
相传在2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系。同学们我们来观察以下地面的图案,看看能从中发现什么数量关系?
问题1:
苏科版
八年级数学上册
二、课堂导入
在生活中是否仔细观察过建筑工人在建筑工地上的施工细节,建筑工人通常对于屋顶的倾斜角度和房间的对角线长度等这种比较难以实地测量的数据,一般会将它们放在一个直角三角形中去求,你们知道是为什么吗?
问题2:
苏科版
八年级数学上册
二、课堂导入
同学们,其实生活中有不少场景都有运用到今天即将所要学习的直角三角形勾股定理,例如,刚刚提到的测量屋顶的倾斜角度和房间的对角线长度等,这就是今天即将要学习的勾股定理的实际运用。通过这种联系,我们可以更好地理解数学知识的实际意义,数学其实与我们的实际生活密切相关。
苏科版
八年级数学上册
三、新知讲授
同学们还记得我们刚刚提到的毕达哥拉斯朋友家的地面图案嘛?我们现在来一起研究。
苏科版
八年级数学上册
三、新知讲授
如图,在等腰三角形ABC中,∠C=90°,以AC为边作正方形P,以BC为边作正方形Q,以斜边AB为边作正方形R。请同学们以小组为单位思考,观察图形思考下列问题:
(1)三个正方形的面积之间有什么关系?
(2)等腰直角三角形ABC三边长度之间存在什么关系?
苏科版
八年级数学上册
三、新知讲授
同学们以小组为单位合作探究上述两个问题。
提示:这三个正方形的面积有怎样的等量关系?
怎么想到的呢?
苏科版
八年级数学上册
三、新知讲授
(1)以等腰直角三角形两直角边为边长的小正方形的面积和,等于以斜边为大正方形的面积;
(2)等腰直角三角形两直角边的平方和等于斜边的平方。
其实我们不难发现:
苏科版
八年级数学上册
三、新知讲授
同学们,这些平时看似平淡无奇的现象是不是有的时候却蕴含着深刻的道理呀!作为青少年的我们也要有一颗善于发现问题的眼睛,在生活中对于平时的现象要勤于思考,积极主动探索里面的奥秘,学会观察和记录生活中的细微变化,其实知识就在我们身边!
苏科版
八年级数学上册
三、新知讲授
既然等腰直角三角形的三边之间具有“两直角边的平方和等于斜边的平方”这一性质,那么一般的直角三角形是否也有这样的性质呢?
苏科版
八年级数学上册
三、新知讲授
请同学们试着表示出在下面网格中直角三角形三边衍生的正方形的面积之间的关系,看看三个正方形的面积有着怎样的等量关系。
苏科版
八年级数学上册
在计算正方形的面积时,学会使用“割”和“补”两种常见处理面积的方法来求正方形a的面积。
提示:
三、新知讲授
苏科版
八年级数学上册
请同学们拿出手中的方格纸,试着在方格纸中再画出几个一般形状的直角三角形,用类似于上面研究方法,小组合作一起探究一般性的直角三角形三边之间的等量关系。
三、新知讲授
苏科版
八年级数学上册
直角三角形三边衍生的正方形的面积之间的关系:
三、新知讲授
苏科版
八年级数学上册
请同学们对于一般性的直角三角形三边之间的等量关系进行合理适当的猜想。
命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么有
三、新知讲授
苏科版
八年级数学上册
对于上面提出的猜想,同学们是否能对其进行合理规范的证明呢?
三、新知讲授
苏科版
八年级数学上册
那接下来我们一起来了解一下我国古代第一位证明勾股定理的数学家——赵爽是如何证明的
三、新知讲授
苏科版
八年级数学上册
赵爽的主要贡献是约在222年深入研究了《周髀算经》,该书简明扼要地总结出中国古代勾股算术的深奥原理。其中一段530余字的“勾股圆方图”注文是数学史上极有价值的文献。他详细解释了《周髀算经》中勾股定理。
三、新知讲授
苏科版
八年级数学上册
赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,赵爽根据此图指出:四个全等的直角三角形(橙色)可以如图围成一个大正方形,中空的部分是一个小正方形(蓝色)。
三、新知讲授
苏科版
八年级数学上册
(1)一个小直角三角形的面积为 ;
(2)图1的面积为 ;
(3)图2的面积为 ;
(4)图1和图2的面积是否相等?你知道它们是通过何种变换得到的吗?
三、新知讲授
苏科版
八年级数学上册
下面我们通过视频动画来看看它们是怎么变换的:
三、新知讲授
苏科版
八年级数学上册
赵爽所用的这种方法是我国古代数学家常用的“出入相补法”。在西方,人们称勾股定理为毕达哥拉斯定理。因此“赵爽弦图”这个图案被选为2002年在北京召开的国际数学家大会的会徽。
三、新知讲授
苏科版
八年级数学上册
同学们我们古人赵爽利用“出入相补法”的原理证明出了勾股定理,体现了我国古代数学成就之高。纵观中国数学发展史,中国古代在数学方面的成就足以开一座陈列馆,体现出我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。所以我们要以我国优秀的民族文化感到骄傲。在这个信息多元的时代依然要保持对我们中华优秀传统文化的自豪感。
三、新知讲授
苏科版
八年级数学上册
古人赵爽的证明思想证实了命题1的正确性,命题1与直角三角形的边有关,我国把它称作勾股定理。
勾股定理 如果直角三角形的两直角边长分别为a和b,斜边长为c,那么
三、新知讲授
苏科版
八年级数学上册
在Rt△ABC中
∵∠C=90°
∴
符号语言:
三、新知讲授
苏科版
八年级数学上册
四、例题讲解
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a;
例1:设直角三角形的两条直角边长分别为a和b,斜边长为c:
苏科版
八年级数学上册
(1)已知a=6,c=10,求b;
例1:设直角三角形的两条直角边长分别为a和b,斜边长为c:
解:由勾股定理公式 ,已知a=6,c=10,代入公式得
四、例题讲解
苏科版
八年级数学上册
(2)已知a=5,b=12,求c;
例1:设直角三角形的两条直角边长分别为a和b,斜边长为c:
解:由勾股定理公式 ,已知a=5,b=12,代入公式得
四、例题讲解
苏科版
八年级数学上册
四、例题讲解
(3)已知c=25,b=15,求a;
例1:设直角三角形的两条直角边长分别为a和b,斜边长为c:
解:由勾股定理公式 ,已知c=25,b=15,代入公式得
苏科版
八年级数学上册
已知直角三角形的两个边的长度就可以根据勾股定理求出另外第三边的长度。此外,在一些没有明确长度是斜边长还是直角边的时候,要分类讨论。
四、例题讲解
苏科版
八年级数学上册
注意:同学们在平时做题时,要积累常见的勾股数,利于提高解题的速度。
常见的勾股数:
(3,4,5 ) 勾三股四弦五
(5,12,13 )
(6,8,10):连续的偶数
(8,15,17 )
它们的倍数也是勾股数!
四、例题讲解
苏科版
八年级数学上册
例2:如图,图中所有的三角形都是直角三角形,四边形都是正方形。已知正方形A,B,C,D的边长分别12,16,9,12,求最大正方形E的面积。
四、例题讲解
苏科版
八年级数学上册
解:由正方形A和B的边长为12和16,可知正方形A的面积
正方形B的面积
同理:由正方形C和D的边长为9和12,可知正方形C的面积
正方形D的面积
四、例题讲解
苏科版
八年级数学上册
最后:勾股定理探究过程可得,两个中等的正方形面积分别为400和225;由此得出最大正方形E的面积为400+225=625.
总结:在充分理解勾股定理探究过程的基础上,掌握直角三角形三边衍生出的正方形的数量关系。
四、例题讲解
苏科版
八年级数学上册
课本p28的练习1-3题
五、课堂练习
苏科版
八年级数学上册
本节课你学了哪些内容:
1.在探究直角三角形三边关系时,得到有关三边延申出的正方形面积的等量关系是什么?
直角三角形三边衍生的正方形的面积之间的关系:
六、课堂小结
苏科版
八年级数学上册
本节课你学了哪些内容:
2.勾股定理的内容是什么?几何语言怎么表示?
勾股定理 如果直角三角形的两直角边长分别为a和b,斜边长为c,那么
在Rt△ABC中
∵∠C=90°
∴
几何语言:
六、课堂小结
苏科版
八年级数学上册
六、课堂小结
本节课你学了哪些内容:
3.能说说“赵爽弦图”是如何证明勾股定理的吗?
利用旋转前后的面积相等
苏科版
八年级数学上册
七、课后作业
1.必做题:教材课后的练习题;查阅相关资料和书籍了解其他的有关勾股定理的证明;
2.选做题:练习册B组;
苏科版
八年级数学上册
再见!
苏科版
八年级数学上册
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
