天津市梅江中学八年级数学下册18.2.2 菱形课件2
文档属性
| 名称 | 天津市梅江中学八年级数学下册18.2.2 菱形课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 16.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-02 19:05:40 | ||
图片预览

文档简介
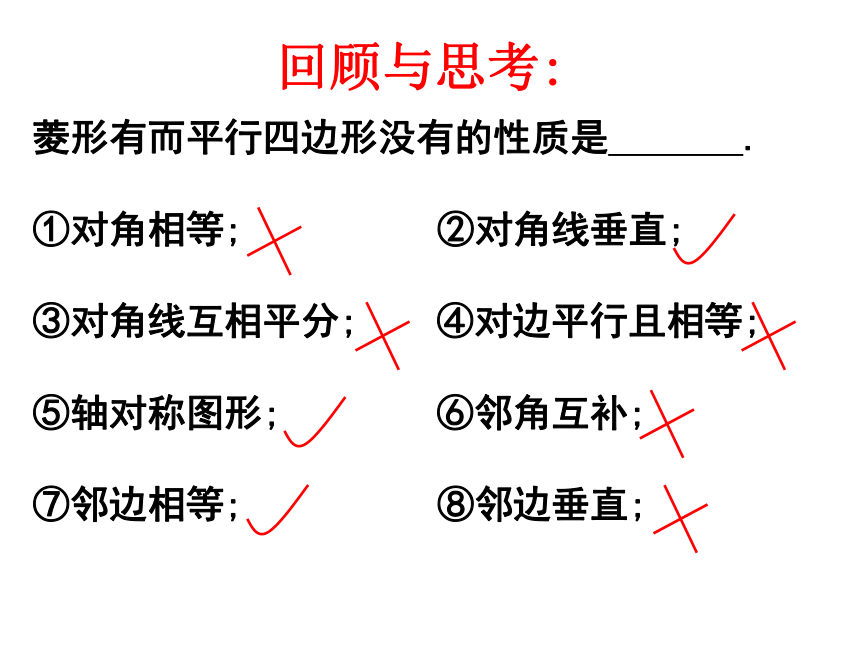
课件12张PPT。18.2.2 菱形 (2)菱形有而平行四边形没有的性质是 .
①对角相等; ②对角线垂直;
③对角线互相平分; ④对边平行且相等;
⑤轴对称图形; ⑥邻角互补;
⑦邻边相等; ⑧邻边垂直;
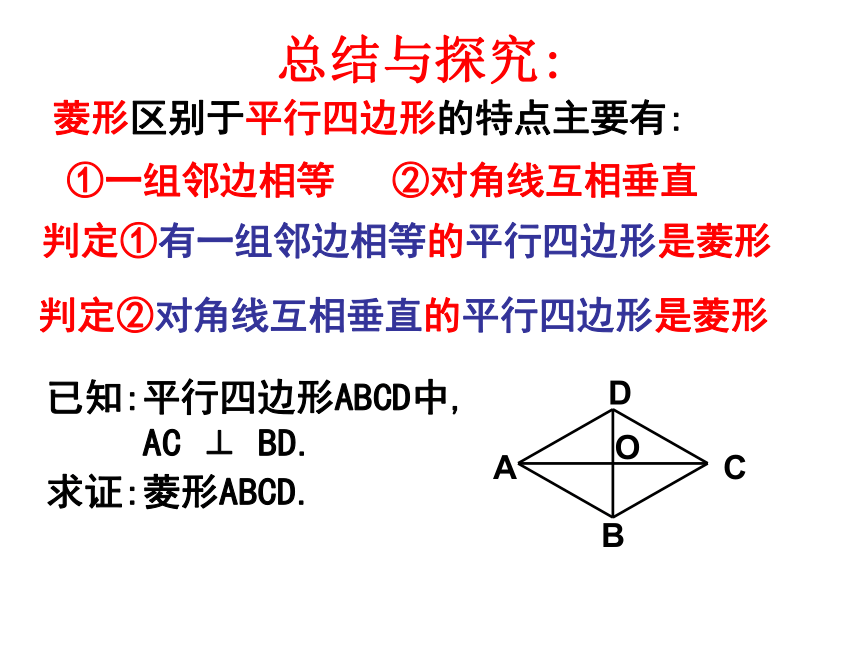
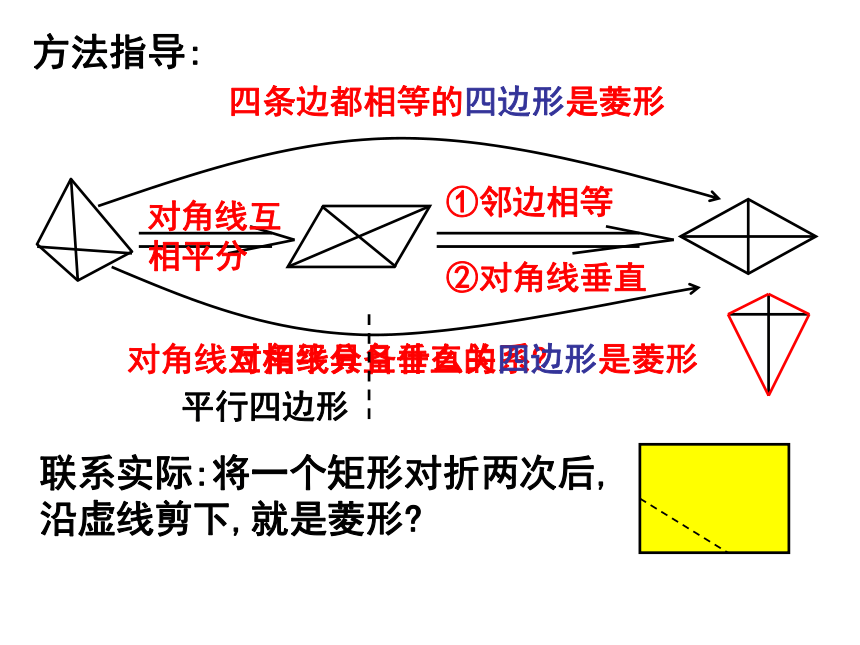
回顾与思考:菱形区别于平行四边形的特点主要有:①一组邻边相等②对角线互相垂直判定①有一组邻边相等的平行四边形是菱形判定②对角线互相垂直的平行四边形是菱形总结与探究:方法指导:①邻边相等②对角线垂直四条边都相等的四边形是菱形对角线互
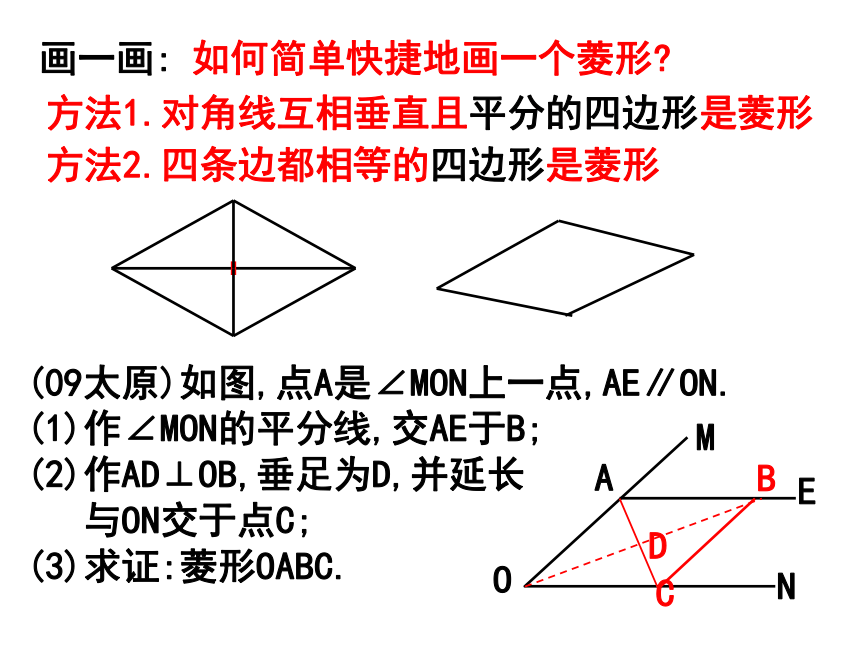
相平分对角线互相平分且垂直的四边形是菱形平行四边形画一画:如何简单快捷地画一个菱形?方法2.四条边都相等的四边形是菱形方法1.对角线互相垂直且平分的四边形是菱形(09太原)如图,点A是∠MON上一点,AE∥ON.
(1)作∠MON的平分线,交AE于B;
(2)作AD⊥OB,垂足为D,并延长
与ON交于点C;
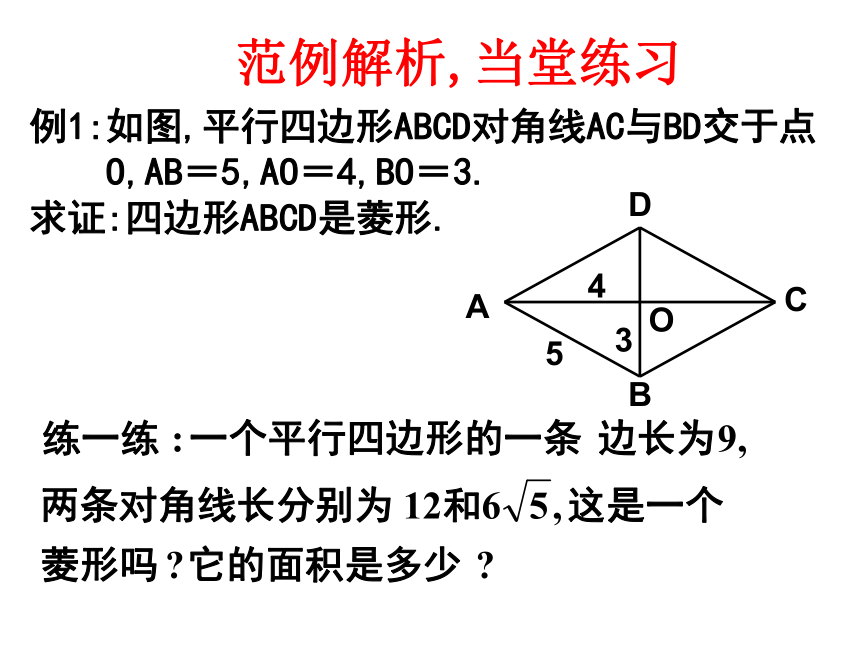
(3)求证:菱形OABC.BDC例1:如图,平行四边形ABCD对角线AC与BD交于点
O,AB=5,AO=4,BO=3.
求证:四边形ABCD是菱形.范例解析,当堂练习例2(嘉兴)如图,平行四边形ABCD中,AE⊥BC,
AF⊥CD,BD与AE,AF分别交于点G,H,AG=AH.
求证:四边形ABCD是菱形.范例解析,当堂练习例3:△ABC中,∠ACB=90o,AD平分∠CAB,
CH⊥AB,DE⊥AB.
求证:菱形CDEF.ABCHDEF范例解析,当堂练习例4:矩形ABCD对角线AC的垂直平分线分别交AD,
BC于点E,F.
求证:四边形AFCE是菱形.范例解析,当堂练习1.平行四边形ABCD中,BD平分∠ABC.
求证:菱形ABCD.过关训练2.(江苏)如图,将纸片△ABC(AB>AC)沿过点A的直线折叠,折痕为AD,展开纸片(如图1);再次折叠纸片,使点A,D重合,折痕为EF(如图2).展开后,小明认为△AEF是等腰三角形;连接DE,DF,小明认为四边形AEDF是菱形.
你觉得呢?过关训练3.如图,两张宽度相同的长方形纸片交叉放置,
(1)判断重合部分的形状?
(2)若宽度为4cm,夹角是30度,求阴影面积.过关训练ABCDEF4cm30o8
①对角相等; ②对角线垂直;
③对角线互相平分; ④对边平行且相等;
⑤轴对称图形; ⑥邻角互补;
⑦邻边相等; ⑧邻边垂直;
回顾与思考:菱形区别于平行四边形的特点主要有:①一组邻边相等②对角线互相垂直判定①有一组邻边相等的平行四边形是菱形判定②对角线互相垂直的平行四边形是菱形总结与探究:方法指导:①邻边相等②对角线垂直四条边都相等的四边形是菱形对角线互
相平分对角线互相平分且垂直的四边形是菱形平行四边形画一画:如何简单快捷地画一个菱形?方法2.四条边都相等的四边形是菱形方法1.对角线互相垂直且平分的四边形是菱形(09太原)如图,点A是∠MON上一点,AE∥ON.
(1)作∠MON的平分线,交AE于B;
(2)作AD⊥OB,垂足为D,并延长
与ON交于点C;
(3)求证:菱形OABC.BDC例1:如图,平行四边形ABCD对角线AC与BD交于点
O,AB=5,AO=4,BO=3.
求证:四边形ABCD是菱形.范例解析,当堂练习例2(嘉兴)如图,平行四边形ABCD中,AE⊥BC,
AF⊥CD,BD与AE,AF分别交于点G,H,AG=AH.
求证:四边形ABCD是菱形.范例解析,当堂练习例3:△ABC中,∠ACB=90o,AD平分∠CAB,
CH⊥AB,DE⊥AB.
求证:菱形CDEF.ABCHDEF范例解析,当堂练习例4:矩形ABCD对角线AC的垂直平分线分别交AD,
BC于点E,F.
求证:四边形AFCE是菱形.范例解析,当堂练习1.平行四边形ABCD中,BD平分∠ABC.
求证:菱形ABCD.过关训练2.(江苏)如图,将纸片△ABC(AB>AC)沿过点A的直线折叠,折痕为AD,展开纸片(如图1);再次折叠纸片,使点A,D重合,折痕为EF(如图2).展开后,小明认为△AEF是等腰三角形;连接DE,DF,小明认为四边形AEDF是菱形.
你觉得呢?过关训练3.如图,两张宽度相同的长方形纸片交叉放置,
(1)判断重合部分的形状?
(2)若宽度为4cm,夹角是30度,求阴影面积.过关训练ABCDEF4cm30o8
