勾股定理(1)
图片预览



文档简介
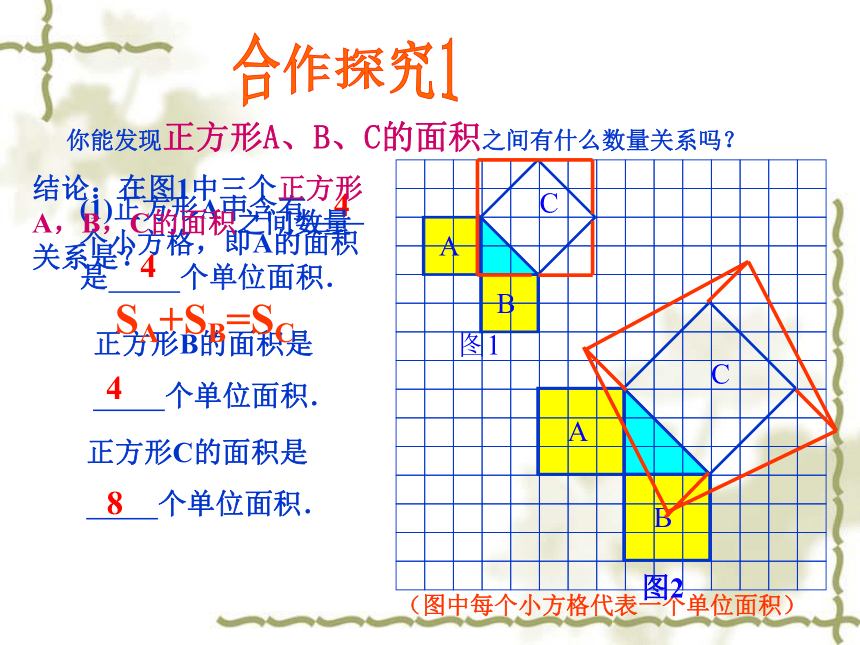
课件31张PPT。人教版八年级(下)第十八章勾股定理一ACB你对直角三角形有了哪些认识了呢?这幅图有什么特殊的含义吗? 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了A、B、C面积之间的数量关系进而发现直角三角形三边的某种数量关系. 我们也来观察右图中的地面,你也能发现A、B、C面积之间有什么数量关系吗?(图中每个小方格代表一个单位面积)(1)正方形A中含有____ 个小方格,即A的面积是 个单位面积.正方形B的面积是
个单位面积.正方形C的面积是
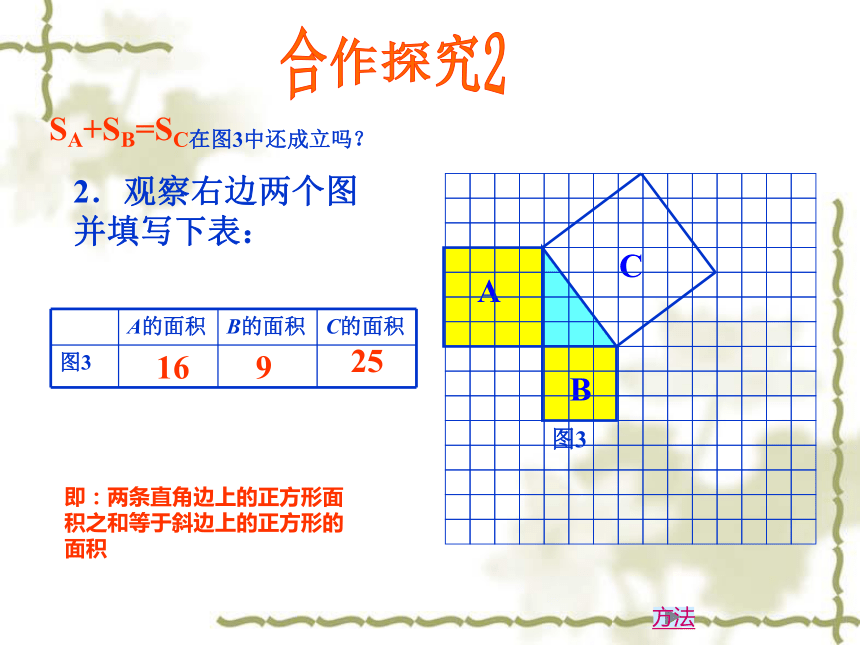
个单位面积.4484合作探究1结论:在图1中三个正方形A,B,C的面积之间数量关系是? SA+SB=SC 你能发现正方形A、B、C的面积之间有什么数量关系吗?2.观察右边两个图并填写下表:16925合作探究2 SA+SB=SC在图3中还成立吗?方法即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
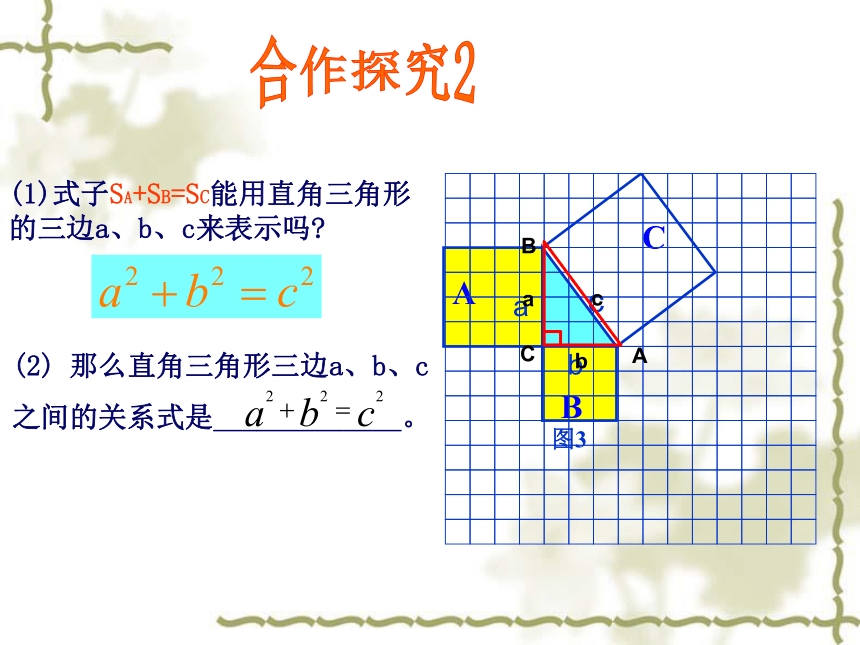
ABC图3(1)式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗?(2) 那么直角三角形三边a、b、c
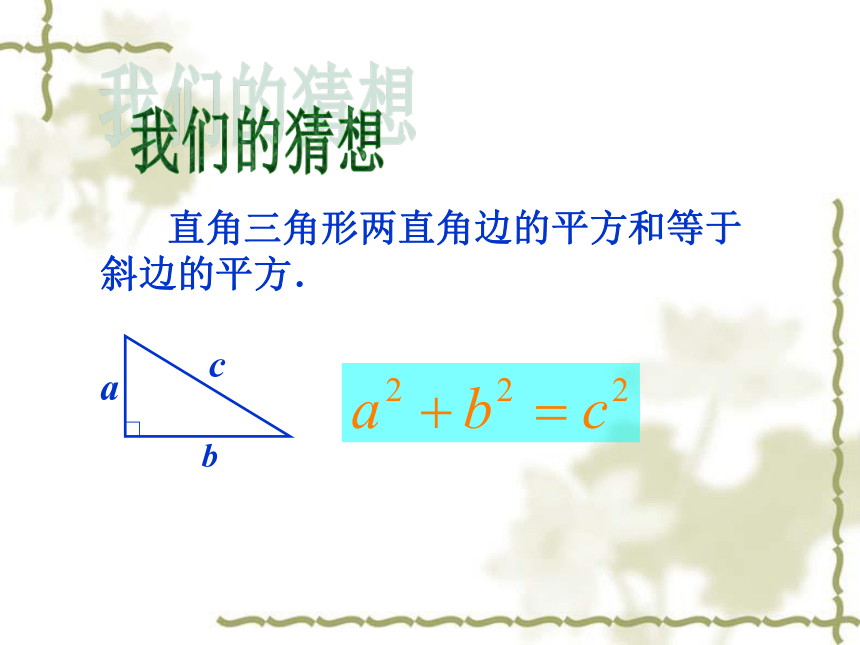
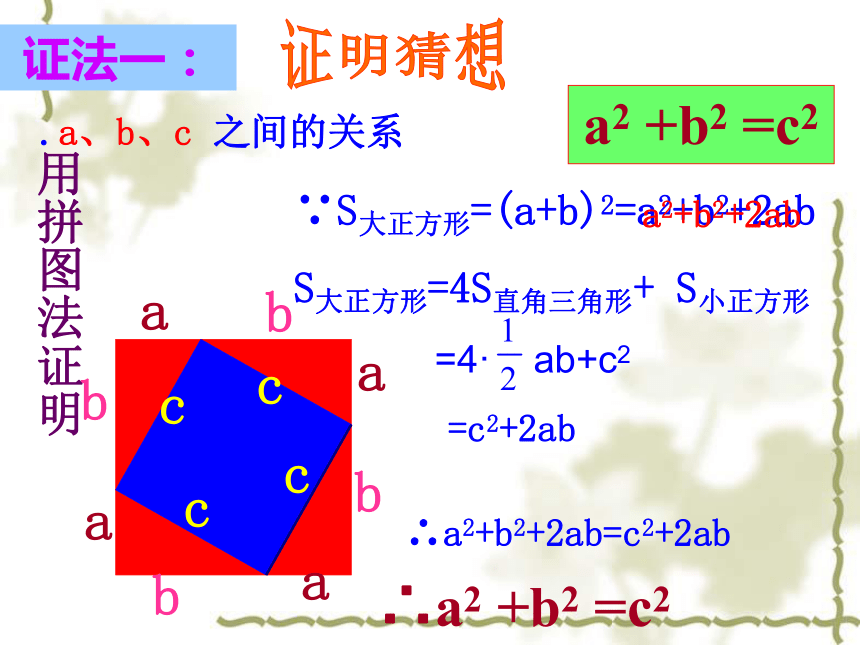
之间的关系式是_____________。合作探究2 直角三角形两直角边的平方和等于斜边的平方.我们的猜想用拼图法证明∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
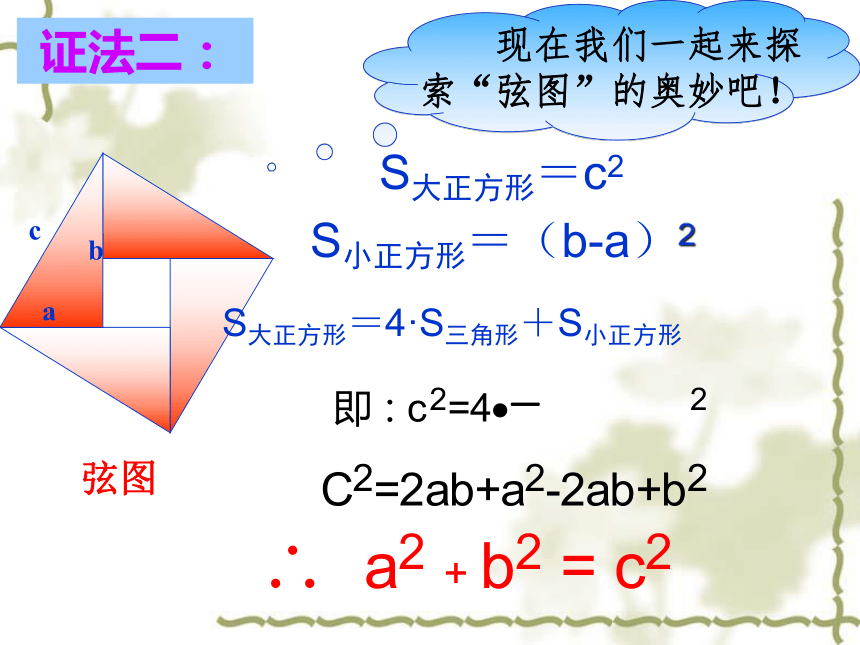
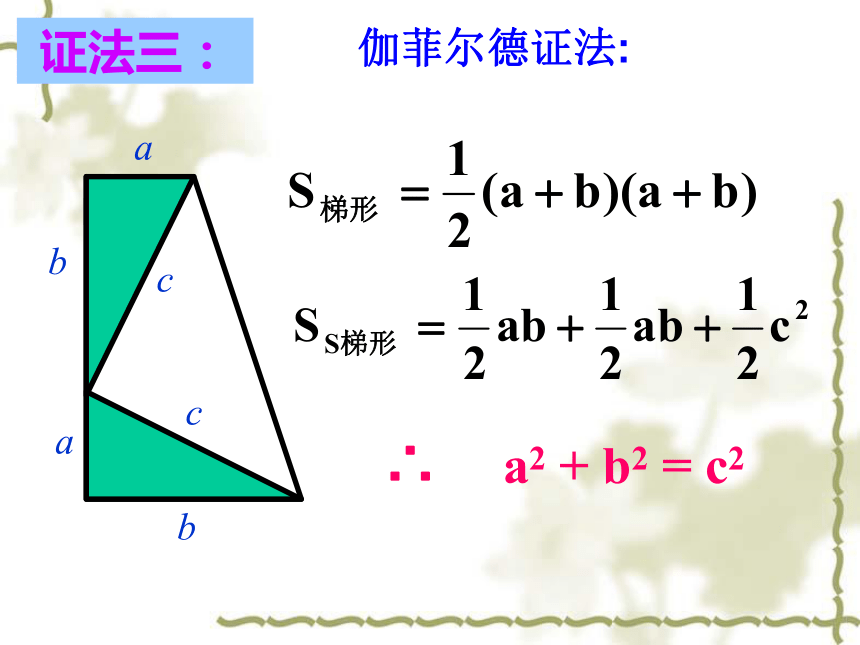
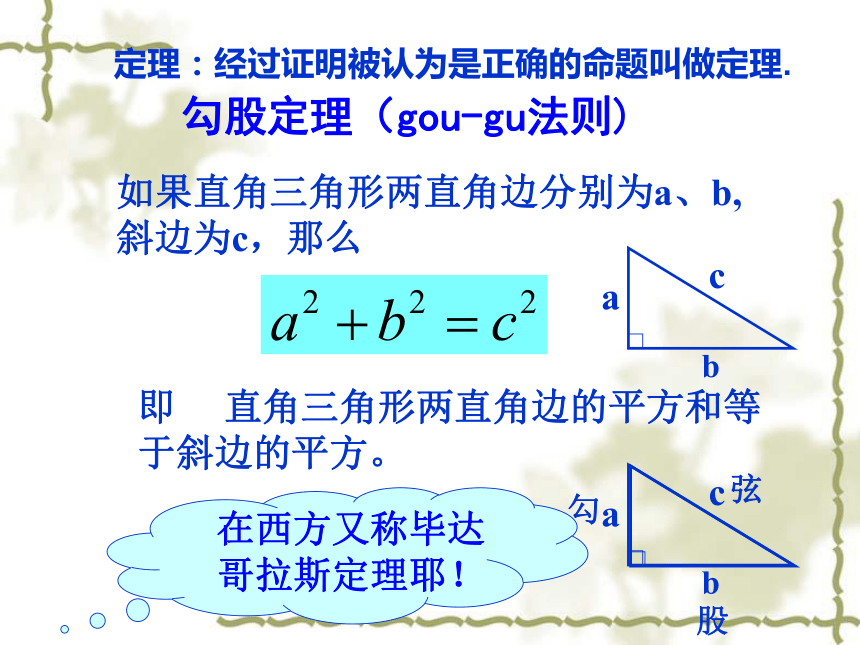
∴a2+b2+2ab=c2+2ab∴a2 +b2 =c2a2+b2+2ab证法一:证明猜想abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形弦图 现在我们一起来探索“弦图”的奥妙吧!证法二:证法三:aabbcc伽菲尔德证法:∴ a2 + b2 = c2 如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦定理:经过证明被认为是正确的命题叫做定理. 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a2勾股史话 商高定理:
商高是公元前 十一世纪的中国人。当时中国的朝代是西周, 是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作 “商高定理”。 商高定理就是勾股定理哦!毕达哥拉斯定理: 毕达哥拉斯 “勾股定理”在国外,尤其在西方被称为“毕达哥拉斯定理”或“百牛定理”.
相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。他发现勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”. 毕达哥拉斯(毕达哥拉斯,前572~前497),西方理性数学创始人,古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年.
课堂 练 习1、求下图中字母所代表的正方形的面积。225400A81225B6251442.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做求出下列直角三角形中未知的边巩固反馈比一比看看谁算得快!求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x 如图,受台风“麦莎”影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?回归生活小结变式训练如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49再变式训练在本节课中,我们……1.本节主线2.学习内容及方法 学习了著名的勾股定理,还知道从特殊到一般的探索方法.3.本节的数学思想 借助于图形的面积来探索、验证数学结论的数形结合思想。4.学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现.这节课我们还认识了两位伟大的数学家,受到了数学文化辉煌历史的教育。1.必做题:课本第113页,习题19.1 第1, 2题.
2.选做题:课本第116页“阅读与思考”,了解勾股定理的多种证法.
3.上网查阅了解勾股定理的发现和证明并写一篇关于关于它的小论文.作业 科学上没有平坦的大道,真理长河中有无数的礁石险滩。只有不畏攀登的采药者,只有不怕巨浪的弄潮儿,才能登上高峰采得仙草,深入水底觅得骊珠。让我们做生活中
数学的有心人同学们再见1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )A.3 米 B.4 米 C.5米 D.6米C345 或 2、已知:Rt△ABC中,AB=4,AB=3,则BC的长为___________ .3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( ) A 2、4、6C 4、6、8BB 6、8、10D 8、10、124、湖的两端有A、B两点,从与BA方向成直角的公元前方向上的点C测得CA=130米,CB=120米,则AB为( ) A.50米 B.120米 C.100米 D.130米130120?A1、判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2( )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
( )
××能力比拼(1)求墙的高度? (精确到0.1米)解:∵∠ACB=90°AB=3,BC=1≈2.8(米)(2)若梯子的顶端下滑50厘米,
底端将向外水平移动多少米?AA′BB′3m1mC∴ AB2=AC2+BC2 有一架3米长的梯子靠在墙上,刚好与墙头对齐,此时梯脚B与墙脚C的距离是1米。探究1
个单位面积.正方形C的面积是
个单位面积.4484合作探究1结论:在图1中三个正方形A,B,C的面积之间数量关系是? SA+SB=SC 你能发现正方形A、B、C的面积之间有什么数量关系吗?2.观察右边两个图并填写下表:16925合作探究2 SA+SB=SC在图3中还成立吗?方法即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
ABC图3(1)式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗?(2) 那么直角三角形三边a、b、c
之间的关系式是_____________。合作探究2 直角三角形两直角边的平方和等于斜边的平方.我们的猜想用拼图法证明∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab+c2
=c2+2ab
∴a2+b2+2ab=c2+2ab∴a2 +b2 =c2a2+b2+2ab证法一:证明猜想abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形弦图 现在我们一起来探索“弦图”的奥妙吧!证法二:证法三:aabbcc伽菲尔德证法:∴ a2 + b2 = c2 如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦定理:经过证明被认为是正确的命题叫做定理. 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a2勾股史话 商高定理:
商高是公元前 十一世纪的中国人。当时中国的朝代是西周, 是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作 “商高定理”。 商高定理就是勾股定理哦!毕达哥拉斯定理: 毕达哥拉斯 “勾股定理”在国外,尤其在西方被称为“毕达哥拉斯定理”或“百牛定理”.
相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。他发现勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”. 毕达哥拉斯(毕达哥拉斯,前572~前497),西方理性数学创始人,古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年.
课堂 练 习1、求下图中字母所代表的正方形的面积。225400A81225B6251442.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做求出下列直角三角形中未知的边巩固反馈比一比看看谁算得快!求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x 如图,受台风“麦莎”影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?回归生活小结变式训练如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49再变式训练在本节课中,我们……1.本节主线2.学习内容及方法 学习了著名的勾股定理,还知道从特殊到一般的探索方法.3.本节的数学思想 借助于图形的面积来探索、验证数学结论的数形结合思想。4.学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现.这节课我们还认识了两位伟大的数学家,受到了数学文化辉煌历史的教育。1.必做题:课本第113页,习题19.1 第1, 2题.
2.选做题:课本第116页“阅读与思考”,了解勾股定理的多种证法.
3.上网查阅了解勾股定理的发现和证明并写一篇关于关于它的小论文.作业 科学上没有平坦的大道,真理长河中有无数的礁石险滩。只有不畏攀登的采药者,只有不怕巨浪的弄潮儿,才能登上高峰采得仙草,深入水底觅得骊珠。让我们做生活中
数学的有心人同学们再见1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )A.3 米 B.4 米 C.5米 D.6米C345 或 2、已知:Rt△ABC中,AB=4,AB=3,则BC的长为___________ .3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( ) A 2、4、6C 4、6、8BB 6、8、10D 8、10、124、湖的两端有A、B两点,从与BA方向成直角的公元前方向上的点C测得CA=130米,CB=120米,则AB为( ) A.50米 B.120米 C.100米 D.130米130120?A1、判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2( )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
( )
××能力比拼(1)求墙的高度? (精确到0.1米)解:∵∠ACB=90°AB=3,BC=1≈2.8(米)(2)若梯子的顶端下滑50厘米,
底端将向外水平移动多少米?AA′BB′3m1mC∴ AB2=AC2+BC2 有一架3米长的梯子靠在墙上,刚好与墙头对齐,此时梯脚B与墙脚C的距离是1米。探究1
