5.3平行线的性质 自主学习解答题专题提升训练题(含解析) 人教版七年级数学下册
文档属性
| 名称 | 5.3平行线的性质 自主学习解答题专题提升训练题(含解析) 人教版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 384.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 09:19:58 | ||
图片预览




文档简介
人教版七年级数学下册《5.3平行线的性质》
自主学习解答题专题提升训练题
1.把下列命题改写成“如果…,那么…”
(1)同旁内角互补,两直线平行;
(2)a+b=0,则a与b互为相反数;
(3)平行于同一条直线的两条直线平行.
2.如图,已知,,则.完成下面的说理过程(填空).
解:∵
∴________(两直线平行,同位角相等)
∵( )
∴________( )
∴________( )
∴(等量代换)
3.如图,已知,,若,求的度数.
4.如图,已知,,平分,求和的度数.
5.如图,,,直线与,的延长线分别交于点,.求证:.
6.如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.试说明:∠A=∠F.
请同学们补充下面的解答过程,并填空(理由或数学式).
解:∵∠AGB=∠DGF( )
∠AGB=∠EHF(已知),
∴∠DGF=∠EHF( ),
∴DG∥ ( ),
∴∠D= (两直线平行,同位角相等)
∵∠D=∠C(已知),
∴ =∠C,
∴DF∥ ( ),
∴∠A=∠F( )
7.如图,在中,,垂足为,点在上,,垂足为.
(1)与平行吗?为什么?
(2)如果,那么吗?为什么?
8.如图,于点,于点,平分交于点,点为线段延长线上一点,,求证:
9.如图,已知,平分,平分,交于点, 求证.
10.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射,如图,水面与水杯下沿平行,光线从水中射向空气时发生折射,光线变成,点G在射线上,已知,求的度数.
11.如图,已知,.
(1)这一结论正确吗?为什么?
(2)你能得出和=这两个结论吗?若能,写出你的推理过程.
12.已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
(1)求证:CE∥DF;
(2)若∠DCE=126°,求∠DEF的度数.
13.如图,在三角形中,点、在边上,点在边上,点在边上,与的延长线交于点,,.
(1)与平行吗?请说明理由;
(2)若,求的度数.
14.完成下面的推理过程:
如图,已知EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C.
(1)求证:AB∥MN;
(2)若∠BMN=140°,∠ADM=25°,求∠BAD的度数.
证明:(1)∵EF⊥AC,DB⊥AC,
∴∠CFE=∠CMD=90°(________________)
∴EF∥DM(同位角相等,两直线平行)
∴∠2=∠CDM(________________)
∵∠1=∠2(已知)
∴∠1=∠CDM(等量代换)
∴MN∥CD(________________)
∴∠C=∠________(两直线平行,同位角相等)
∵∠3=∠C(已知)
∴∠3=∠AMN(等量代换)
∴AB∥MN(内错角相等,两直线平行)
(2)∵AB∥MN(已证)
∴∠BMN+∠B=180°(________________)
∵∠BMN=140°(已知)
∴∠B=40°
∵∠BAD+∠B+∠ADB=180°(________________)
∴∠BAD=180°-∠B-∠ADB=180°-40°-25°=115°
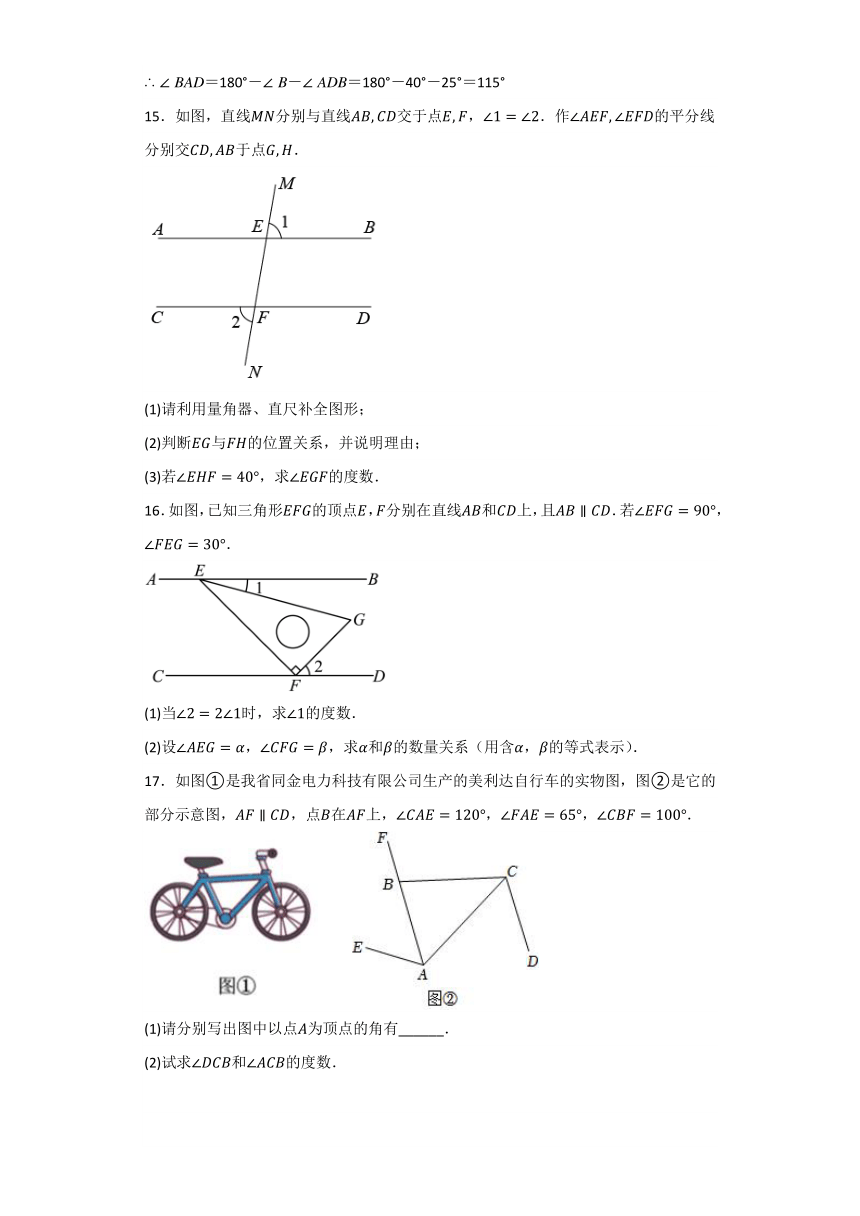
15.如图,直线分别与直线交于点,.作的平分线分别交于点.
(1)请利用量角器、直尺补全图形;
(2)判断与的位置关系,并说明理由;
(3)若,求的度数.
16.如图,已知三角形的顶点,分别在直线和上,且.若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
17.如图①是我省同金电力科技有限公司生产的美利达自行车的实物图,图②是它的部分示意图,,点在上,,,.
(1)请分别写出图中以点为顶点的角有______.
(2)试求和的度数.
18.已知,和中,,.试探究:
(1)如图1,与的关系是______,并说明理由;
(2)如图2,写出与的关系,并说明理由;
(3)根据上述探究,请归纳得到一个真命题.
19.问题情景:如图1,.
(1)观察猜想:若,.则的度数为__________.
(2)探究问题:在图1中探究,、与之间有怎样的等量关系?并说明理由.
(3)拓展延伸:若将图1变为图2,题设的条件不变,此时、与之间有怎样的等量关系?并说明理由.
20.如图,已知,交于点,.
(1)(如图1)求证:.
(2)若在射线上取一点,连接、,使得,且(如图2),求的度数.
(3)在(2)的条件下,过点作,且比大,求的度数.
参考答案
1.解:(1)如果同旁内角互补,那么两直线平行;
(2)如果,那么a与b互为相反数;
(3)如果两条直线平行于同一条直线,那么这两条直线平行.
2.解:由题意得:∵
∴(两直线平行,同位角相等)
∵(已知)
∴DE(内错角相等,两直线平行)
∴ (两直线平行,内错角相等)
∴(等量代换).
故答案为:;已知;DE;内错角相等,两直线平行;;两直线平行,内错角相等.
3.解:如图,
∵,
∴∠1=∠4,
∵,
∴∠3=∠4,
∴∠3=∠1,
∵,
∴∠3=75 .
4.解:∵(已知)
∴(两直线平行,同位角相等)
∵(已知)
∴(等量代换)
∵平分(已知)
∴(角平分线的意义)
∵(已知)
∴(两直线平行,内错角相等)
∴(等量代换)
∵(已证)
∴(等量代换)
5.证明:∵,
∴.
∵,
∴.
∴.
∴.
6.解:和是对顶角,
,
故答案为:对顶角;
,,进行等量代换,
;
故答案为:等量代换;
和是同位角且,
,
故答案为:,同位角相等;
,与是同位角
故答案为:;
,,经过等量代换,
,
故答案为:;
,并且两个角是内错角,
,
故答案为:,内错角相等;
,与是内错角,
故答案为:内错角相等.
7.解:(1)CD∥EF,
理由:∵CD⊥AB,EF⊥AB,
∴∠CDF=∠EFB=90°,
∴CD∥EF.
(2)DG∥BC,
理由:∵CD∥EF,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC.
8.证明:∵AB⊥BC于点B,DC⊥BC于点C,
∴∠B+∠C=180°,
∴AB∥CF,
∴∠BAF+∠F=180°,
又∵∠BAF=∠EDF,
∴∠EDF+∠F=180°,
∴ED∥AF,
∴∠ADE=∠DAF,∠EDC=∠F,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DAF=∠F.
9.证明:∵
∴
∵平分,平分
∴,
∴
∴
∴.
10.解:∵
∴
∵
∴
11.解:(1)正确
,
又,
.
.
(2)能得出,的结论.
由(1),得
.
.
12.(1)证明:∵∠1+∠2=180°,C,D是直线AB上两点,
∴∠1+∠DCE=180°,
∴∠2=∠DCE,
∴CE∥DF;
(2)解:∵CE∥DF,∠DCE=126°,
∴∠CDF=180°﹣∠DCE=180°﹣126°=54°,
∵DE平分∠CDF,
∴∠CDE=∠CDF=27°,
∵EF∥AB,
∴∠DEF=∠CDE=27°.
13.解:(1)平行
∵,
∴,
∴,
∵,
∴,
∴;
(2)由(1)得,,
∴,
∴,
∵,
∴.
14.(1)解:垂直的定义;两直线平行,同位角相等;内错角相等,两直线平行;∠AMN;;
(2)解:两直线平行,同旁内角互补;三角形的内角和定理
15.解:(1)按要求作图如下:
(2),理由如下:
∵∠1是∠AEF的对顶角,
∴∠1=∠AEF,
∵∠1=∠2,
∴∠2=∠AEF,
∴,
∴∠EFD=∠AEF,
∵GE平分∠AEF,HF平分∠EFD,
∴∠GEF=∠AEF=∠EFD=∠EFH,
∴;
(3)∵,
∴∠EHF=∠HFD=40°,
∵,
∴∠HFD=∠EGF,
∴∠EGF=40°.
16.(1)解:∵,
∴,即,
∵,,,
∴,
∴.
(2)解:如图所示,过点作,
∴,
∵,
∴,
∴,
∴,
即,
∵在中,,,
∴,
∴,
∵,,
∴.
17.(1)解:图中以点为顶点的角有,,.
故答案为:,,.
(2)∵,,
∴.
∵,
∴,
,
∴.
∴的度数为,的度数为.
18.(1)解:,理由如下:
如下图,
∵AB∥DE,
∴∠B=∠1,
又∵BC∥EF,
∴∠1=∠E,
∴∠B=∠E;
故答案为:;
(2)解:,理由如下:
如下图,
∵AB∥DE,
∴∠B+∠1=180°,
又∵BC∥EF,
∴∠E=∠1,
∴∠B+∠E=180°
故答案为:;
(3)解:由题意得:如果两个角的两边分别平行,那么这两个角相等或者互补.
19.(1)解:如图所示,过点P作,
∵,,
∴,
∴,
∴,
故答案为:;
(2)解:,理由如下:
如图所示,过点P作,
∵,,
∴,
∴,
∴;
(3)解:,理由如下:
如图所示,过点P作,
∵,,
∴,
∴,
∵,
∴,
∴.
20.(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴
∵,
∴,
∵,
∴;
(3)解:∵,
∴,
∵,
∴
∵比大,
∴比大,即
∵,
∴,
∴.
自主学习解答题专题提升训练题
1.把下列命题改写成“如果…,那么…”
(1)同旁内角互补,两直线平行;
(2)a+b=0,则a与b互为相反数;
(3)平行于同一条直线的两条直线平行.
2.如图,已知,,则.完成下面的说理过程(填空).
解:∵
∴________(两直线平行,同位角相等)
∵( )
∴________( )
∴________( )
∴(等量代换)
3.如图,已知,,若,求的度数.
4.如图,已知,,平分,求和的度数.
5.如图,,,直线与,的延长线分别交于点,.求证:.
6.如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.试说明:∠A=∠F.
请同学们补充下面的解答过程,并填空(理由或数学式).
解:∵∠AGB=∠DGF( )
∠AGB=∠EHF(已知),
∴∠DGF=∠EHF( ),
∴DG∥ ( ),
∴∠D= (两直线平行,同位角相等)
∵∠D=∠C(已知),
∴ =∠C,
∴DF∥ ( ),
∴∠A=∠F( )
7.如图,在中,,垂足为,点在上,,垂足为.
(1)与平行吗?为什么?
(2)如果,那么吗?为什么?
8.如图,于点,于点,平分交于点,点为线段延长线上一点,,求证:
9.如图,已知,平分,平分,交于点, 求证.
10.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射,如图,水面与水杯下沿平行,光线从水中射向空气时发生折射,光线变成,点G在射线上,已知,求的度数.
11.如图,已知,.
(1)这一结论正确吗?为什么?
(2)你能得出和=这两个结论吗?若能,写出你的推理过程.
12.已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
(1)求证:CE∥DF;
(2)若∠DCE=126°,求∠DEF的度数.
13.如图,在三角形中,点、在边上,点在边上,点在边上,与的延长线交于点,,.
(1)与平行吗?请说明理由;
(2)若,求的度数.
14.完成下面的推理过程:
如图,已知EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C.
(1)求证:AB∥MN;
(2)若∠BMN=140°,∠ADM=25°,求∠BAD的度数.
证明:(1)∵EF⊥AC,DB⊥AC,
∴∠CFE=∠CMD=90°(________________)
∴EF∥DM(同位角相等,两直线平行)
∴∠2=∠CDM(________________)
∵∠1=∠2(已知)
∴∠1=∠CDM(等量代换)
∴MN∥CD(________________)
∴∠C=∠________(两直线平行,同位角相等)
∵∠3=∠C(已知)
∴∠3=∠AMN(等量代换)
∴AB∥MN(内错角相等,两直线平行)
(2)∵AB∥MN(已证)
∴∠BMN+∠B=180°(________________)
∵∠BMN=140°(已知)
∴∠B=40°
∵∠BAD+∠B+∠ADB=180°(________________)
∴∠BAD=180°-∠B-∠ADB=180°-40°-25°=115°
15.如图,直线分别与直线交于点,.作的平分线分别交于点.
(1)请利用量角器、直尺补全图形;
(2)判断与的位置关系,并说明理由;
(3)若,求的度数.
16.如图,已知三角形的顶点,分别在直线和上,且.若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
17.如图①是我省同金电力科技有限公司生产的美利达自行车的实物图,图②是它的部分示意图,,点在上,,,.
(1)请分别写出图中以点为顶点的角有______.
(2)试求和的度数.
18.已知,和中,,.试探究:
(1)如图1,与的关系是______,并说明理由;
(2)如图2,写出与的关系,并说明理由;
(3)根据上述探究,请归纳得到一个真命题.
19.问题情景:如图1,.
(1)观察猜想:若,.则的度数为__________.
(2)探究问题:在图1中探究,、与之间有怎样的等量关系?并说明理由.
(3)拓展延伸:若将图1变为图2,题设的条件不变,此时、与之间有怎样的等量关系?并说明理由.
20.如图,已知,交于点,.
(1)(如图1)求证:.
(2)若在射线上取一点,连接、,使得,且(如图2),求的度数.
(3)在(2)的条件下,过点作,且比大,求的度数.
参考答案
1.解:(1)如果同旁内角互补,那么两直线平行;
(2)如果,那么a与b互为相反数;
(3)如果两条直线平行于同一条直线,那么这两条直线平行.
2.解:由题意得:∵
∴(两直线平行,同位角相等)
∵(已知)
∴DE(内错角相等,两直线平行)
∴ (两直线平行,内错角相等)
∴(等量代换).
故答案为:;已知;DE;内错角相等,两直线平行;;两直线平行,内错角相等.
3.解:如图,
∵,
∴∠1=∠4,
∵,
∴∠3=∠4,
∴∠3=∠1,
∵,
∴∠3=75 .
4.解:∵(已知)
∴(两直线平行,同位角相等)
∵(已知)
∴(等量代换)
∵平分(已知)
∴(角平分线的意义)
∵(已知)
∴(两直线平行,内错角相等)
∴(等量代换)
∵(已证)
∴(等量代换)
5.证明:∵,
∴.
∵,
∴.
∴.
∴.
6.解:和是对顶角,
,
故答案为:对顶角;
,,进行等量代换,
;
故答案为:等量代换;
和是同位角且,
,
故答案为:,同位角相等;
,与是同位角
故答案为:;
,,经过等量代换,
,
故答案为:;
,并且两个角是内错角,
,
故答案为:,内错角相等;
,与是内错角,
故答案为:内错角相等.
7.解:(1)CD∥EF,
理由:∵CD⊥AB,EF⊥AB,
∴∠CDF=∠EFB=90°,
∴CD∥EF.
(2)DG∥BC,
理由:∵CD∥EF,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC.
8.证明:∵AB⊥BC于点B,DC⊥BC于点C,
∴∠B+∠C=180°,
∴AB∥CF,
∴∠BAF+∠F=180°,
又∵∠BAF=∠EDF,
∴∠EDF+∠F=180°,
∴ED∥AF,
∴∠ADE=∠DAF,∠EDC=∠F,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DAF=∠F.
9.证明:∵
∴
∵平分,平分
∴,
∴
∴
∴.
10.解:∵
∴
∵
∴
11.解:(1)正确
,
又,
.
.
(2)能得出,的结论.
由(1),得
.
.
12.(1)证明:∵∠1+∠2=180°,C,D是直线AB上两点,
∴∠1+∠DCE=180°,
∴∠2=∠DCE,
∴CE∥DF;
(2)解:∵CE∥DF,∠DCE=126°,
∴∠CDF=180°﹣∠DCE=180°﹣126°=54°,
∵DE平分∠CDF,
∴∠CDE=∠CDF=27°,
∵EF∥AB,
∴∠DEF=∠CDE=27°.
13.解:(1)平行
∵,
∴,
∴,
∵,
∴,
∴;
(2)由(1)得,,
∴,
∴,
∵,
∴.
14.(1)解:垂直的定义;两直线平行,同位角相等;内错角相等,两直线平行;∠AMN;;
(2)解:两直线平行,同旁内角互补;三角形的内角和定理
15.解:(1)按要求作图如下:
(2),理由如下:
∵∠1是∠AEF的对顶角,
∴∠1=∠AEF,
∵∠1=∠2,
∴∠2=∠AEF,
∴,
∴∠EFD=∠AEF,
∵GE平分∠AEF,HF平分∠EFD,
∴∠GEF=∠AEF=∠EFD=∠EFH,
∴;
(3)∵,
∴∠EHF=∠HFD=40°,
∵,
∴∠HFD=∠EGF,
∴∠EGF=40°.
16.(1)解:∵,
∴,即,
∵,,,
∴,
∴.
(2)解:如图所示,过点作,
∴,
∵,
∴,
∴,
∴,
即,
∵在中,,,
∴,
∴,
∵,,
∴.
17.(1)解:图中以点为顶点的角有,,.
故答案为:,,.
(2)∵,,
∴.
∵,
∴,
,
∴.
∴的度数为,的度数为.
18.(1)解:,理由如下:
如下图,
∵AB∥DE,
∴∠B=∠1,
又∵BC∥EF,
∴∠1=∠E,
∴∠B=∠E;
故答案为:;
(2)解:,理由如下:
如下图,
∵AB∥DE,
∴∠B+∠1=180°,
又∵BC∥EF,
∴∠E=∠1,
∴∠B+∠E=180°
故答案为:;
(3)解:由题意得:如果两个角的两边分别平行,那么这两个角相等或者互补.
19.(1)解:如图所示,过点P作,
∵,,
∴,
∴,
∴,
故答案为:;
(2)解:,理由如下:
如图所示,过点P作,
∵,,
∴,
∴,
∴;
(3)解:,理由如下:
如图所示,过点P作,
∵,,
∴,
∴,
∵,
∴,
∴.
20.(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴
∵,
∴,
∵,
∴;
(3)解:∵,
∴,
∵,
∴
∵比大,
∴比大,即
∵,
∴,
∴.
