7.1探索直线平行的条件 自主学习解答题专题训练(含解析) 苏科版七年级数学下册
文档属性
| 名称 | 7.1探索直线平行的条件 自主学习解答题专题训练(含解析) 苏科版七年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 257.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 00:00:00 | ||
图片预览



文档简介
苏科版七年级数学下册《7.1探索直线平行的条件》
自主学习解答题专题训练
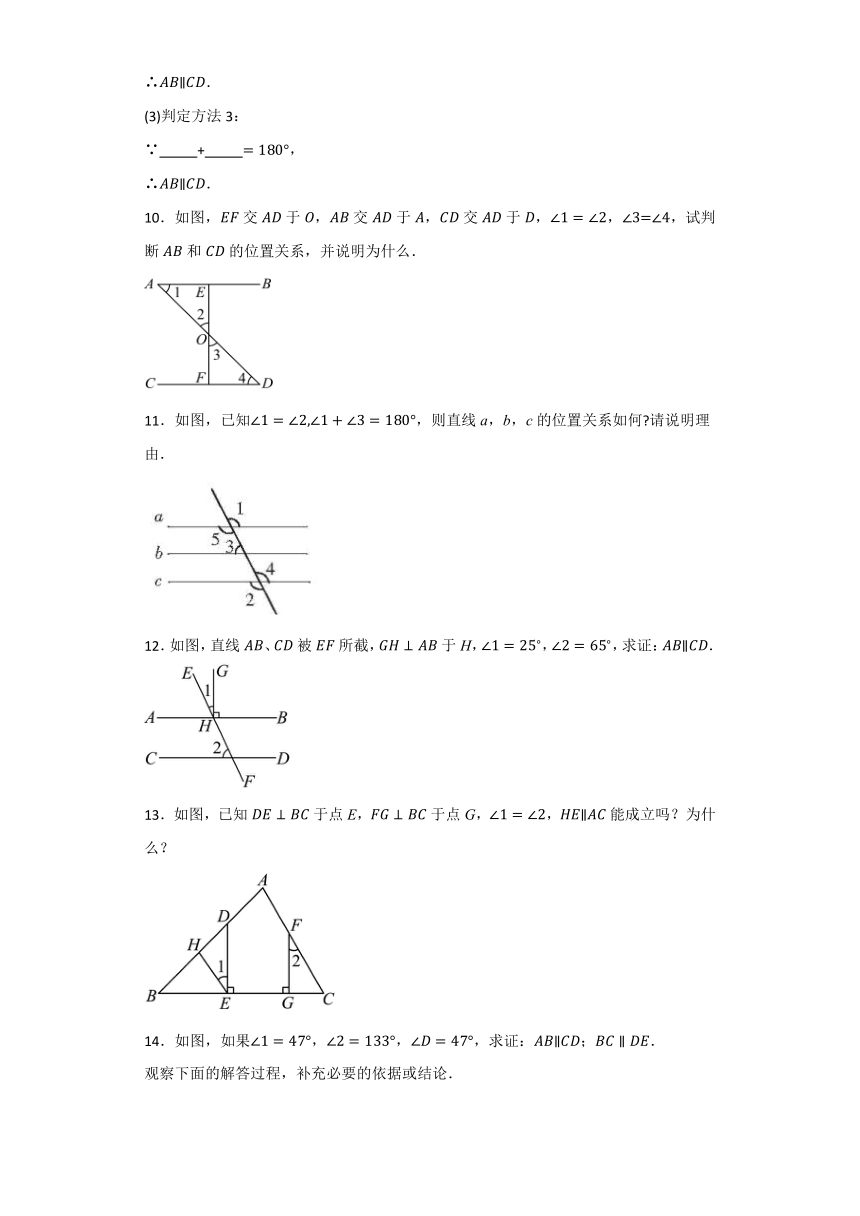
1.如图,直线、被直线所截,和,和,和各是什么位置关系的角?
2.如图,将一张长方形的硬纸片对折,是折痕,把面平摊在桌面上,另一个面不论怎样改变位置,总有与平行,请你说出其中的道理.
3.如图,这是一个由4条线段构成的“鱼”形图案,其中,,,找出图中的平行线,并说明理由.
4.已知:如图,直线与被所截,.求证:.
5.如图,直线,被直线所截,平分,,.求证:.
6.如图,,判断和的位置关系,并说明理由;
7.如图,
(1)如果,那么直线与平行吗?写出理由;
(2)当与之和为时,直线与平行?说明理由.
8.如图,,,垂足分别是,,.
(1)判断与的位置关系;(不需要证明)
(2)求证:.
9.根据如图,写出相应的几何语言:
(1)判定方法1:
∵ = ,
∴.
(2)判定方法2:
∵ = .
∴.
(3)判定方法3:
∵ + ,
∴.
10.如图,交于,交于,交于,,,试判断和的位置关系,并说明为什么.
11.如图,已知,则直线a,b,c的位置关系如何 请说明理由.
12.如图,直线、被所截,于H,,,求证:.
13.如图,已知于点E,于点G,,能成立吗?为什么?
14.如图,如果,求证:;.
观察下面的解答过程,补充必要的依据或结论.
证明:∵(已知),
(______________),
∴(_______________),
又∵(已知),
∴(____________)(等式的性质)
∴(_______________)
又∵(_____________),
∴(等式的性质)
∵(已知),
∴,
∴(___________________________)
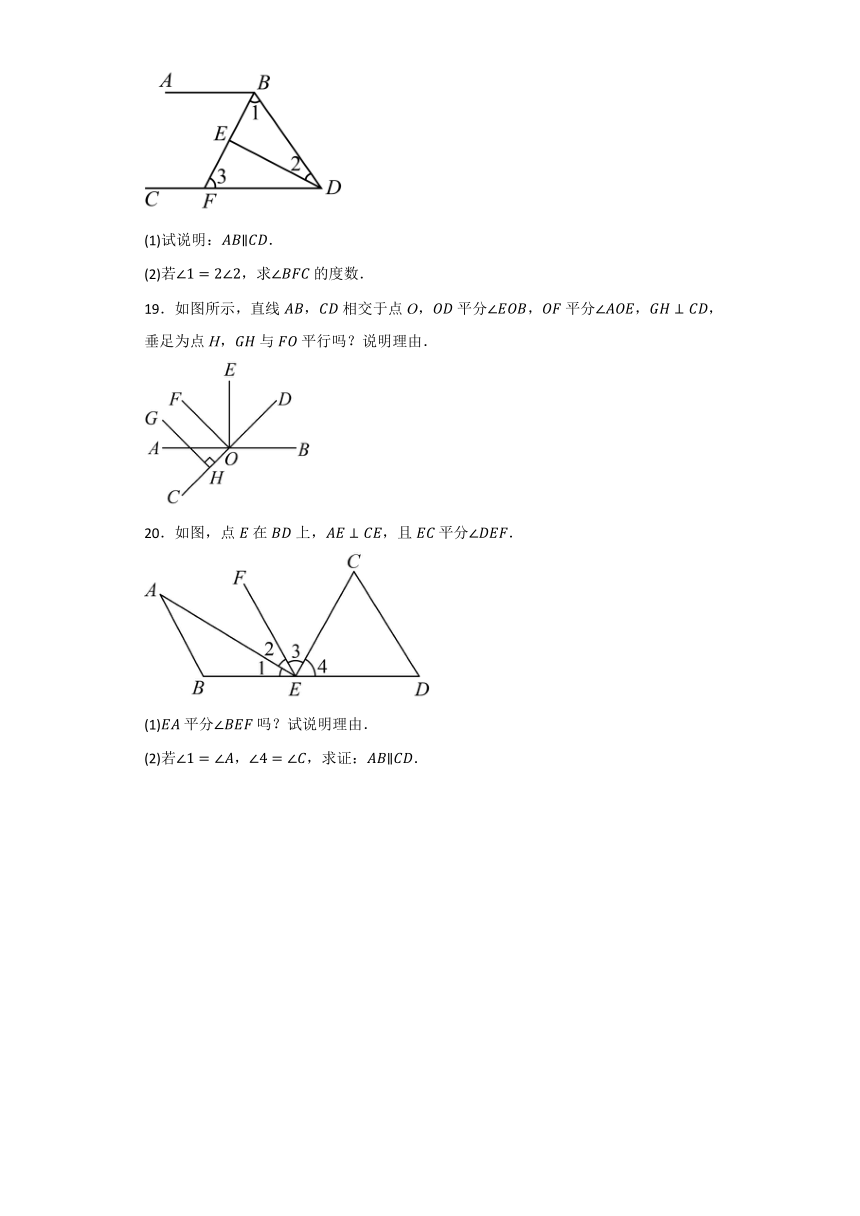
15.如图,已知,,直线和平行吗?为什么?
AI
16.如图,已知平分平分,且与互余.试说明:.
17.已知:如图,点、、三点共线,,,平分,,问:与有什么位置关系?请写出推理过程.
18.如图,的平分线交于E,交于点F,且.
(1)试说明:.
(2)若,求的度数.
19.如图所示,直线相交于点O,平分,平分,,垂足为点H,与平行吗?说明理由.
20.如图,点在上,,且平分.
(1)平分吗?试说明理由.
(2)若,,求证:.
参考答案
1.解:根据图可知,直线、被直线所截,
和是内错角,
和是同旁内角,
和是同位角.
2.解:∵长方形的硬纸片对折,是折痕,
∴,,
∴,
∴另一个面不论怎样改变位置,总有与平行.
3.解:,.
理由:∵,,
∴,
∴;
∵,,
∴,
∴.
4.解:∵(对顶角相等),
又∵(已知),
∴,
∴(同位角相等,两直线平行).
5.解:∵平分,,
∴.
又,
∴.
∴.
6.解:
理由如下:∵,
又∵,
∴,
∴
7.解:(1),理由如下:
∵,
∴(同位角相等,两直线平行);
(2)当时,,理由如下:
∵,,
∴,
∴.
8.(1)解:∵,,
∴.
(2)证明:,,
(等式的性质),
即 ,
(同位角相等,两直线平行).
9.解:(1)判定方法1:
∵,
∴,
故答案为:;;
(2)判定方法2:
∵,
∴,
故答案为:;;
(3)判定方法3:
∵,
∴,
故答案为:;.
10.解:.
理由:,,,
,
∴.
11.解:.理由如下:
因为,所以,所以,
因为,
所以,
所以,所以,
12.证明:∵,
∴
∴
∴
∵
∴
∴.
13.证明:∵,,
∴,
∴,
∵,
∴,
∴.
14.证明:∵(已知),
(对顶角相等),
∴(等量代换),
又∵(已知),
∴()(等式的性质)
∴(同旁内角互补,两直线平行)
又∵(邻补角互补),
∴(等式的性质)
∵(已知),
∴,
∴(内错角相等,两直线平行)
故答案为:对顶角相等;等量代换;;同旁内角互补,两直线平行;邻补角互补;内错角相等,两直线平行.
15.解:平行.
理由:因为,
所以,
又因为,
所以,
所以.
16.解:与互余,
平分平分,
.
.
∴.
17.解:,
证明如下:∵,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴,
∴.
18.(1)证明:∵平分,
∴,
∵,
∴,
∴(同旁内角互补,两直线平行);
(2)解:∵,,
∴,
∵,
∴,
∴.
19.解:,理由如下:
∵平分,平分,
∴,,
∵,
∴,即,
∵,
∴.
20.(1)证明:∵,
∴,
∴
∴.
又∵平分,
∴,
∴,
∴平分.
(2)∵,,,,
∴,,
∴,,
∴.
自主学习解答题专题训练
1.如图,直线、被直线所截,和,和,和各是什么位置关系的角?
2.如图,将一张长方形的硬纸片对折,是折痕,把面平摊在桌面上,另一个面不论怎样改变位置,总有与平行,请你说出其中的道理.
3.如图,这是一个由4条线段构成的“鱼”形图案,其中,,,找出图中的平行线,并说明理由.
4.已知:如图,直线与被所截,.求证:.
5.如图,直线,被直线所截,平分,,.求证:.
6.如图,,判断和的位置关系,并说明理由;
7.如图,
(1)如果,那么直线与平行吗?写出理由;
(2)当与之和为时,直线与平行?说明理由.
8.如图,,,垂足分别是,,.
(1)判断与的位置关系;(不需要证明)
(2)求证:.
9.根据如图,写出相应的几何语言:
(1)判定方法1:
∵ = ,
∴.
(2)判定方法2:
∵ = .
∴.
(3)判定方法3:
∵ + ,
∴.
10.如图,交于,交于,交于,,,试判断和的位置关系,并说明为什么.
11.如图,已知,则直线a,b,c的位置关系如何 请说明理由.
12.如图,直线、被所截,于H,,,求证:.
13.如图,已知于点E,于点G,,能成立吗?为什么?
14.如图,如果,求证:;.
观察下面的解答过程,补充必要的依据或结论.
证明:∵(已知),
(______________),
∴(_______________),
又∵(已知),
∴(____________)(等式的性质)
∴(_______________)
又∵(_____________),
∴(等式的性质)
∵(已知),
∴,
∴(___________________________)
15.如图,已知,,直线和平行吗?为什么?
AI
16.如图,已知平分平分,且与互余.试说明:.
17.已知:如图,点、、三点共线,,,平分,,问:与有什么位置关系?请写出推理过程.
18.如图,的平分线交于E,交于点F,且.
(1)试说明:.
(2)若,求的度数.
19.如图所示,直线相交于点O,平分,平分,,垂足为点H,与平行吗?说明理由.
20.如图,点在上,,且平分.
(1)平分吗?试说明理由.
(2)若,,求证:.
参考答案
1.解:根据图可知,直线、被直线所截,
和是内错角,
和是同旁内角,
和是同位角.
2.解:∵长方形的硬纸片对折,是折痕,
∴,,
∴,
∴另一个面不论怎样改变位置,总有与平行.
3.解:,.
理由:∵,,
∴,
∴;
∵,,
∴,
∴.
4.解:∵(对顶角相等),
又∵(已知),
∴,
∴(同位角相等,两直线平行).
5.解:∵平分,,
∴.
又,
∴.
∴.
6.解:
理由如下:∵,
又∵,
∴,
∴
7.解:(1),理由如下:
∵,
∴(同位角相等,两直线平行);
(2)当时,,理由如下:
∵,,
∴,
∴.
8.(1)解:∵,,
∴.
(2)证明:,,
(等式的性质),
即 ,
(同位角相等,两直线平行).
9.解:(1)判定方法1:
∵,
∴,
故答案为:;;
(2)判定方法2:
∵,
∴,
故答案为:;;
(3)判定方法3:
∵,
∴,
故答案为:;.
10.解:.
理由:,,,
,
∴.
11.解:.理由如下:
因为,所以,所以,
因为,
所以,
所以,所以,
12.证明:∵,
∴
∴
∴
∵
∴
∴.
13.证明:∵,,
∴,
∴,
∵,
∴,
∴.
14.证明:∵(已知),
(对顶角相等),
∴(等量代换),
又∵(已知),
∴()(等式的性质)
∴(同旁内角互补,两直线平行)
又∵(邻补角互补),
∴(等式的性质)
∵(已知),
∴,
∴(内错角相等,两直线平行)
故答案为:对顶角相等;等量代换;;同旁内角互补,两直线平行;邻补角互补;内错角相等,两直线平行.
15.解:平行.
理由:因为,
所以,
又因为,
所以,
所以.
16.解:与互余,
平分平分,
.
.
∴.
17.解:,
证明如下:∵,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴,
∴.
18.(1)证明:∵平分,
∴,
∵,
∴,
∴(同旁内角互补,两直线平行);
(2)解:∵,,
∴,
∵,
∴,
∴.
19.解:,理由如下:
∵平分,平分,
∴,,
∵,
∴,即,
∵,
∴.
20.(1)证明:∵,
∴,
∴
∴.
又∵平分,
∴,
∴,
∴平分.
(2)∵,,,,
∴,,
∴,,
∴.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
