2024年中考数学复习专题练习:全等三角形(含答案)
文档属性
| 名称 | 2024年中考数学复习专题练习:全等三角形(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 149.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 00:00:00 | ||
图片预览

文档简介
2024年中考数学复习专题练习:全等三角形
一、选择题
1.下列说法正确的是( )
A.全等三角形的周长和面积相等 B.全等三角形是指面积相等的两个三角形
C.全等三角形是指形状相同的三角形 D.所有等边三角形是全等三角形
2.如图,点B、F、C、E在一条直线上,∠A=∠D=90°,AB=DE,添加下列选项中的条件,能用HL判定△ABC≌△DEF的是( )
A.AC=DF B.∠B=∠E C.∠ACB=∠DFE D.BC=EF
3.如图,在四边形中,对角线、相交于点,且,,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
4.如图,≌,点在线段上,,则的大小为( )
A. B. C. D.
5.如图,中,,平分,过点作于,测得,,则的周长是( )
A.30 B.24 C.18 D.12
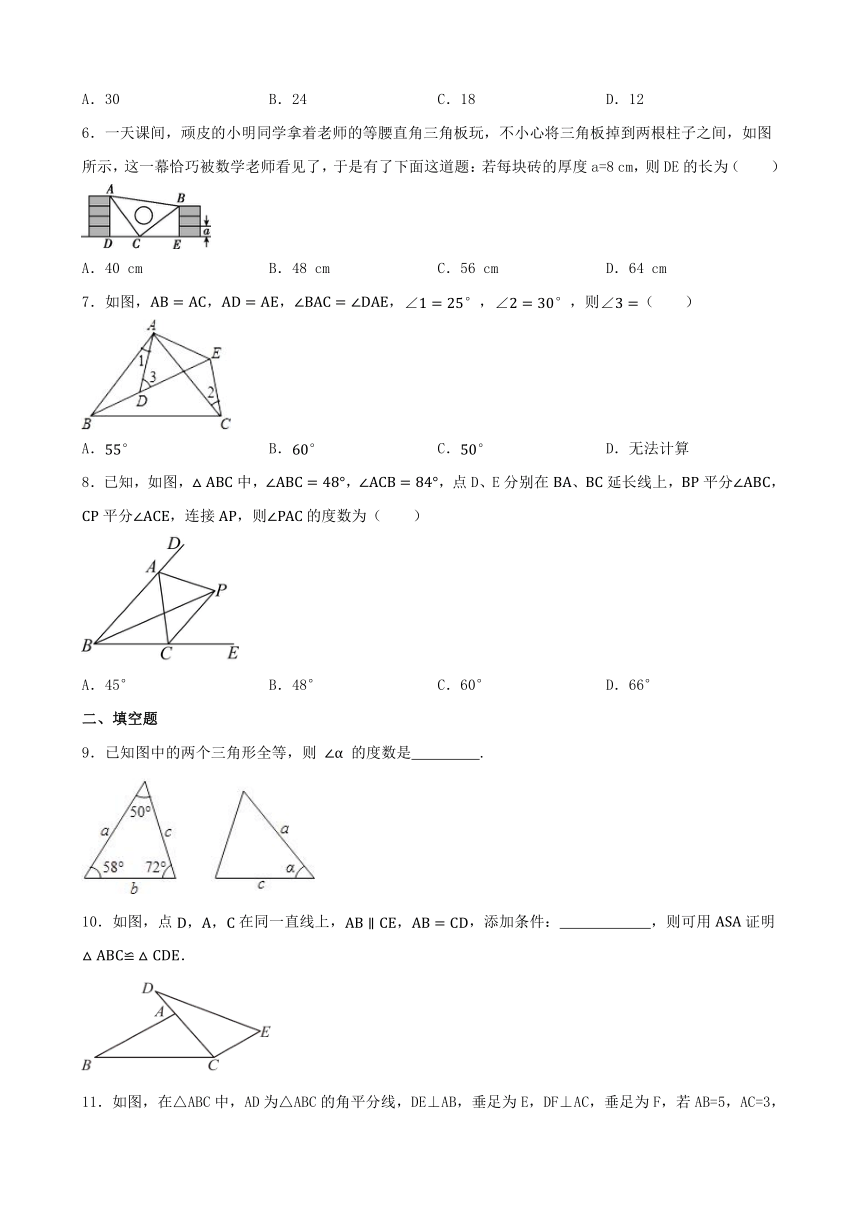
6.一天课间,顽皮的小明同学拿着老师的等腰直角三角板玩,不小心将三角板掉到两根柱子之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题:若每块砖的厚度a=8 cm,则DE的长为( )
A.40 cm B.48 cm C.56 cm D.64 cm
7.如图,,,,,,则( )
A. B. C. D.无法计算
8.已知,如图,中,,,点D、E分别在、延长线上,平分,平分,连接,则的度数为( )
A.45° B.48° C.60° D.66°
二、填空题
9.已知图中的两个三角形全等,则 的度数是 .
10.如图,点在同一直线上,,添加条件: ,则可用证明.
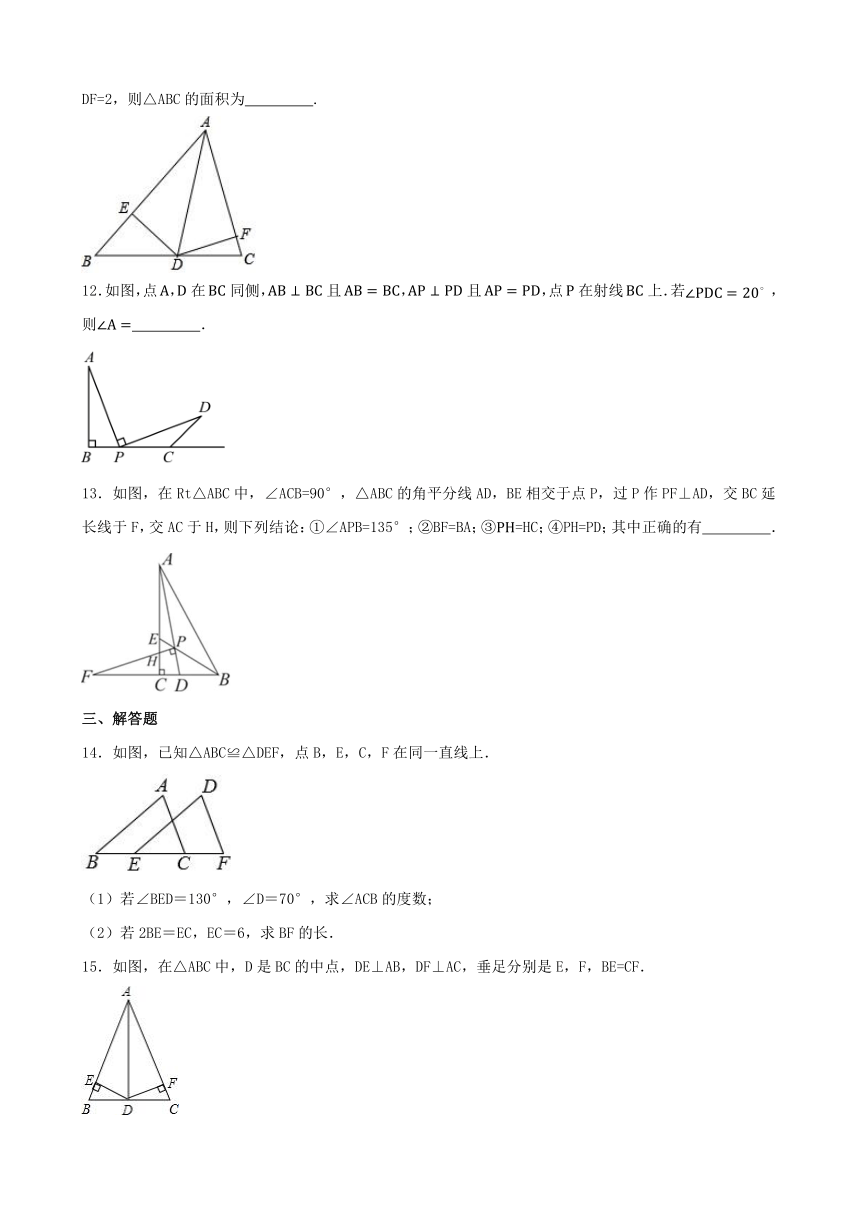
11.如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为 .
12.如图,点,在同侧,且,且,点在射线上.若,则 .
13.如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD,BE相交于点P,过P作PF⊥AD,交BC延长线于F,交AC于H,则下列结论:①∠APB=135°;②BF=BA;③=HC;④PH=PD;其中正确的有 .
三、解答题
14.如图,已知△ABC≌△DEF,点B,E,C,F在同一直线上.
(1)若∠BED=130°,∠D=70°,求∠ACB的度数;
(2)若2BE=EC,EC=6,求BF的长.
15.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
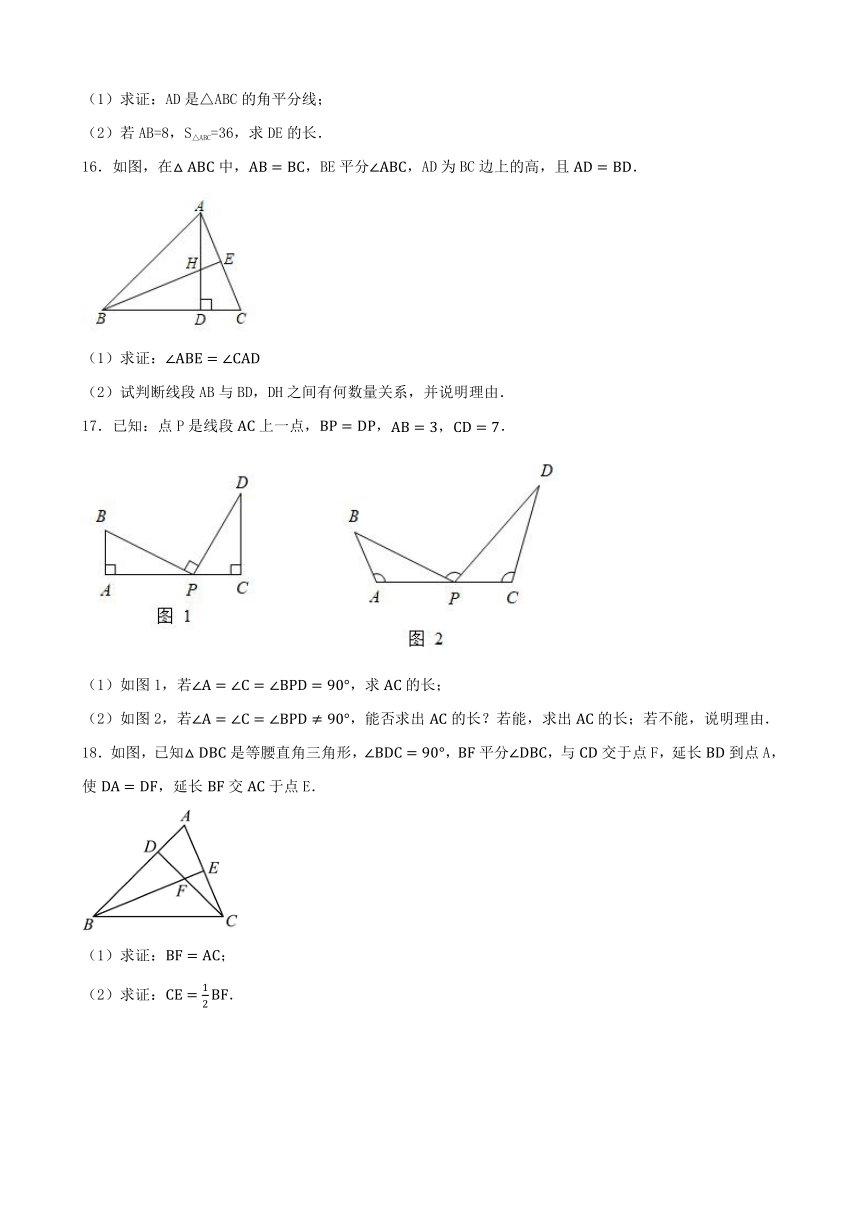
(1)求证:AD是△ABC的角平分线;
(2)若AB=8,S△ABC=36,求DE的长.
16.如图,在中,,BE平分,AD为BC边上的高,且.
(1)求证:
(2)试判断线段AB与BD,DH之间有何数量关系,并说明理由.
17.已知:点P是线段上一点,,.
(1)如图1,若,求的长;
(2)如图2,若,能否求出的长?若能,求出的长;若不能,说明理由.
18.如图,已知是等腰直角三角形,,平分,与交于点F,延长到点A,使,延长交于点E.
(1)求证:;
(2)求证:.
参考答案
1.A
2.D
3.C
4.D
5.B
6.C
7.A
8.D
9.50°
10.∠B=∠D
11.8
12.
13.①②④
14.(1)解:∵∠BED=130°,∠D=70°,
∴∠F=∠BED-∠D=60°,
∵ ABC≌ DEF,
∴∠ACB=∠F=60°
(2)解:∵2BE=EC,EC=6,
∴BE=3,
∴BC=BE+EC=9,
∵ ABC≌ DEF,
∴EF=BC=9,
∴BF=EF+BE=12.
15.(1)∵D是BC 的中点
在Rt△DEB和Rt△DFC中
∴△DEB≌△DFC
∴DE=DF
又 .
∴AD是△ABC的角平分线
(2)解:由(1)得,△DEB≌△DFC
DE=DF
∵S△ABC=36
解得
16.(1)证明:∵AB=BC,BE平分∠ABC,
∴∠ABE=∠CBE,AE=EC,BE⊥AC,
∴∠BEC=∠ADC=90°,
∴∠C+∠DAC=∠C+∠EBC=90°,
∴∠EBC=∠DAC,
∴∠ABE=∠DAC;
(2)解:AB=BD+CD,理由如下:
在△ADC和△BDH中,
,
∴△ADC≌△BDH(AAS),
∴DH=DC,
∴BD+DH=DB+DC=BC=AB.
17.(1)解:∵
∴
∵
∴
∴,
∴.
(2)解:能.
∵,
∴
∵
∴
∴,
∴.
18.(1)证明:∵是等腰直角三角形,
∴,
在和中,
∴,
∴;
(2)证明:∵,
∴
∵,
∴,
∵,
∴,
∴,
∵平分
∴,
在和中,
∴,
∴,
∵,
∴.
一、选择题
1.下列说法正确的是( )
A.全等三角形的周长和面积相等 B.全等三角形是指面积相等的两个三角形
C.全等三角形是指形状相同的三角形 D.所有等边三角形是全等三角形
2.如图,点B、F、C、E在一条直线上,∠A=∠D=90°,AB=DE,添加下列选项中的条件,能用HL判定△ABC≌△DEF的是( )
A.AC=DF B.∠B=∠E C.∠ACB=∠DFE D.BC=EF
3.如图,在四边形中,对角线、相交于点,且,,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
4.如图,≌,点在线段上,,则的大小为( )
A. B. C. D.
5.如图,中,,平分,过点作于,测得,,则的周长是( )
A.30 B.24 C.18 D.12
6.一天课间,顽皮的小明同学拿着老师的等腰直角三角板玩,不小心将三角板掉到两根柱子之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题:若每块砖的厚度a=8 cm,则DE的长为( )
A.40 cm B.48 cm C.56 cm D.64 cm
7.如图,,,,,,则( )
A. B. C. D.无法计算
8.已知,如图,中,,,点D、E分别在、延长线上,平分,平分,连接,则的度数为( )
A.45° B.48° C.60° D.66°
二、填空题
9.已知图中的两个三角形全等,则 的度数是 .
10.如图,点在同一直线上,,添加条件: ,则可用证明.
11.如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为 .
12.如图,点,在同侧,且,且,点在射线上.若,则 .
13.如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD,BE相交于点P,过P作PF⊥AD,交BC延长线于F,交AC于H,则下列结论:①∠APB=135°;②BF=BA;③=HC;④PH=PD;其中正确的有 .
三、解答题
14.如图,已知△ABC≌△DEF,点B,E,C,F在同一直线上.
(1)若∠BED=130°,∠D=70°,求∠ACB的度数;
(2)若2BE=EC,EC=6,求BF的长.
15.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
(1)求证:AD是△ABC的角平分线;
(2)若AB=8,S△ABC=36,求DE的长.
16.如图,在中,,BE平分,AD为BC边上的高,且.
(1)求证:
(2)试判断线段AB与BD,DH之间有何数量关系,并说明理由.
17.已知:点P是线段上一点,,.
(1)如图1,若,求的长;
(2)如图2,若,能否求出的长?若能,求出的长;若不能,说明理由.
18.如图,已知是等腰直角三角形,,平分,与交于点F,延长到点A,使,延长交于点E.
(1)求证:;
(2)求证:.
参考答案
1.A
2.D
3.C
4.D
5.B
6.C
7.A
8.D
9.50°
10.∠B=∠D
11.8
12.
13.①②④
14.(1)解:∵∠BED=130°,∠D=70°,
∴∠F=∠BED-∠D=60°,
∵ ABC≌ DEF,
∴∠ACB=∠F=60°
(2)解:∵2BE=EC,EC=6,
∴BE=3,
∴BC=BE+EC=9,
∵ ABC≌ DEF,
∴EF=BC=9,
∴BF=EF+BE=12.
15.(1)∵D是BC 的中点
在Rt△DEB和Rt△DFC中
∴△DEB≌△DFC
∴DE=DF
又 .
∴AD是△ABC的角平分线
(2)解:由(1)得,△DEB≌△DFC
DE=DF
∵S△ABC=36
解得
16.(1)证明:∵AB=BC,BE平分∠ABC,
∴∠ABE=∠CBE,AE=EC,BE⊥AC,
∴∠BEC=∠ADC=90°,
∴∠C+∠DAC=∠C+∠EBC=90°,
∴∠EBC=∠DAC,
∴∠ABE=∠DAC;
(2)解:AB=BD+CD,理由如下:
在△ADC和△BDH中,
,
∴△ADC≌△BDH(AAS),
∴DH=DC,
∴BD+DH=DB+DC=BC=AB.
17.(1)解:∵
∴
∵
∴
∴,
∴.
(2)解:能.
∵,
∴
∵
∴
∴,
∴.
18.(1)证明:∵是等腰直角三角形,
∴,
在和中,
∴,
∴;
(2)证明:∵,
∴
∵,
∴,
∵,
∴,
∴,
∵平分
∴,
在和中,
∴,
∴,
∵,
∴.
同课章节目录
