2024年中考数学专题训练——圆的综合(含答案)
文档属性
| 名称 | 2024年中考数学专题训练——圆的综合(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 11:18:44 | ||
图片预览


文档简介
2024年中考数学专题训练——圆的综合
1.如图,是的直径,点,在上,,交于点,.
(1)求的度数;
(2)若是的切线,与的延长线交于点,.直接写出图中阴影部分的面积.
2.如图,已知 是 的直径, , 与圆交于点 ,过点 作 于点 ,与 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 半径长为3, ,求 的长;
(3)若 与圆交于点 , 为 的中点, ,求 的度数.
3.如图,在Rt△ 中, , 平分∠ , 交 于点 ,△ 的外接圆⊙ 与边 相交于点 ,过点 作 的垂线交 于 ,交 于 ,交⊙ 于点 ,连接 .
(1)求证:BC是⊙O的切线;
(2)若sin∠G= ,AB=16,求⊙O的直径.
4.如图,在平面直角坐标系中,点A的坐标为(4,0),B是y轴正半轴上的一个动点,以OA为直径作圆,交AB于点C.
(1)求证:△AOB∽△ACO;
(2)当∠OAB=30°时,求点C到x轴的距离;
(3)求 的最大值.
5.在平面直角坐标系xOy中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作d(M).
(1)已知点E(0,4),
①直接写出d(点E)的值;
②直线y=kx+4(k≠0)与x轴交于点F,当d(线段EF)取最小值时,求k的取值范围;
(2)⊙T的圆心为T(7,t),半径为1.若d(⊙T)<11,请直接写出t的取值范围.
6.AB是⊙O的直径,C点在⊙O上,F是AC的中点,OF的延长线交⊙O于点D,点E在AB的延长线上,∠A=∠BCE.
(1)求证:CE是⊙O的切线;
(2)若BC=BE,判定四边形OBCD的形状,并说明理由.
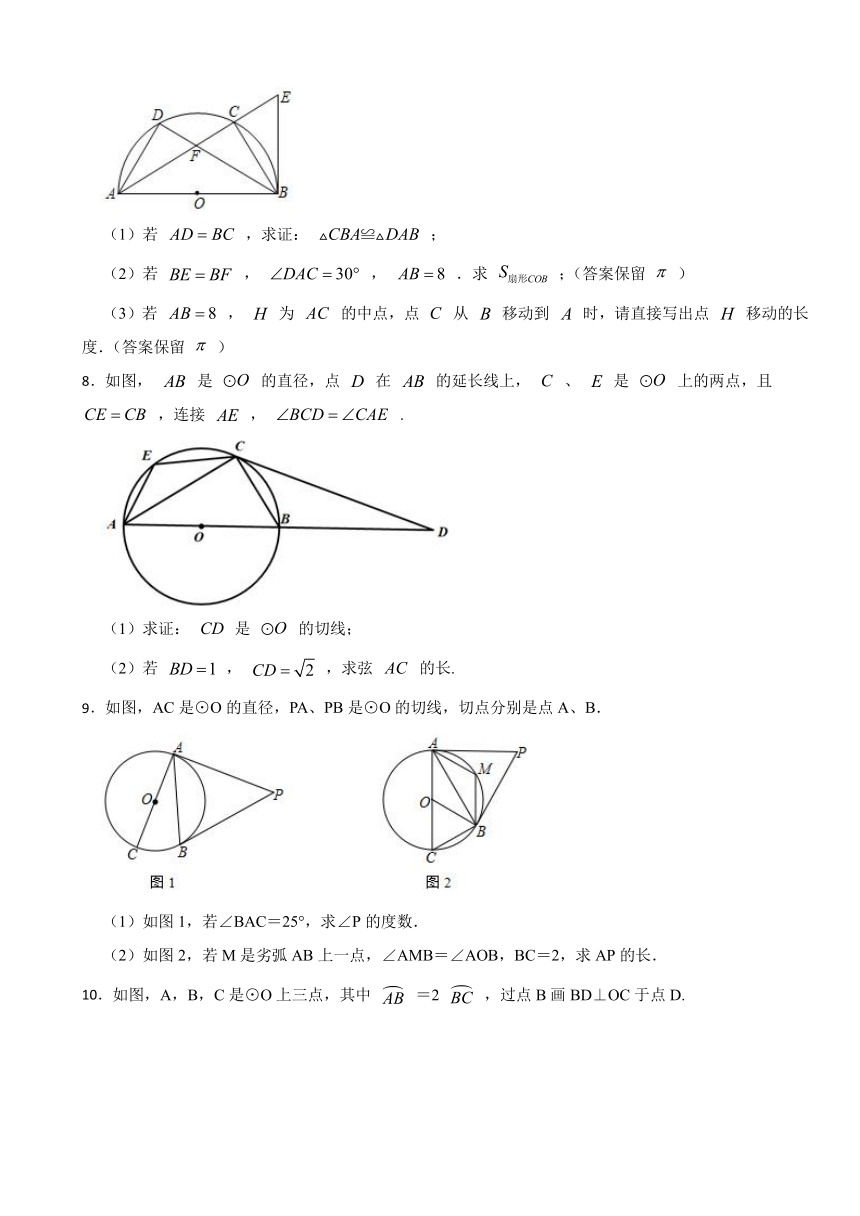
7.如图, 是半圆 的直径, 是半圆 上不同于 、 两点的任意一点, 是半圆 上一动点, 与 相交于点 , 是半圆 所在圆的切线,与 的延长线相交于点 .
(1)若 ,求证: ;
(2)若 , , .求 ;(答案保留 )
(3)若 , 为 的中点,点 从 移动到 时,请直接写出点 移动的长度.(答案保留 )
8.如图, 是 的直径,点 在 的延长线上, 、 是 上的两点,且 ,连接 , .
(1)求证: 是 的切线;
(2)若 , ,求弦 的长.
9.如图,AC是⊙O的直径,PA、PB是⊙O的切线,切点分别是点A、B.
(1)如图1,若∠BAC=25°,求∠P的度数.
(2)如图2,若M是劣弧AB上一点,∠AMB=∠AOB,BC=2,求AP的长.
10.如图,A,B,C是⊙O上三点,其中 =2 ,过点B画BD⊥OC于点D.
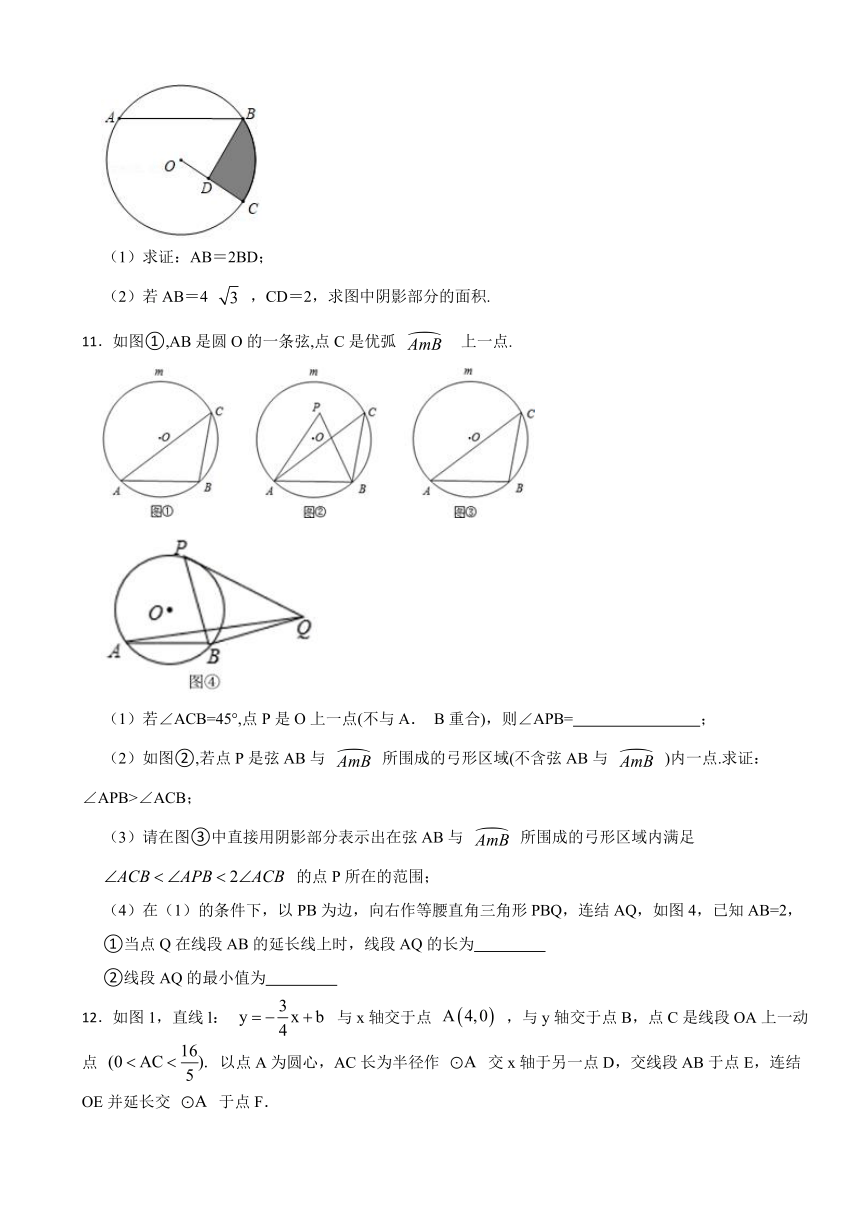
(1)求证:AB=2BD;
(2)若AB=4 ,CD=2,求图中阴影部分的面积.
11.如图①,AB是圆O的一条弦,点C是优弧 上一点.
(1)若∠ACB=45°,点P是O上一点(不与A. B重合),则∠APB= ;
(2)如图②,若点P是弦AB与 所围成的弓形区域(不含弦AB与 )内一点.求证:∠APB>∠ACB;
(3)请在图③中直接用阴影部分表示出在弦AB与 所围成的弓形区域内满足
的点P所在的范围;
(4)在(1)的条件下,以PB为边,向右作等腰直角三角形PBQ,连结AQ,如图4,已知AB=2,
①当点Q在线段AB的延长线上时,线段AQ的长为
②线段AQ的最小值为
12.如图1,直线l: 与x轴交于点 ,与y轴交于点B,点C是线段OA上一动点 以点A为圆心,AC长为半径作 交x轴于另一点D,交线段AB于点E,连结OE并延长交 于点F.
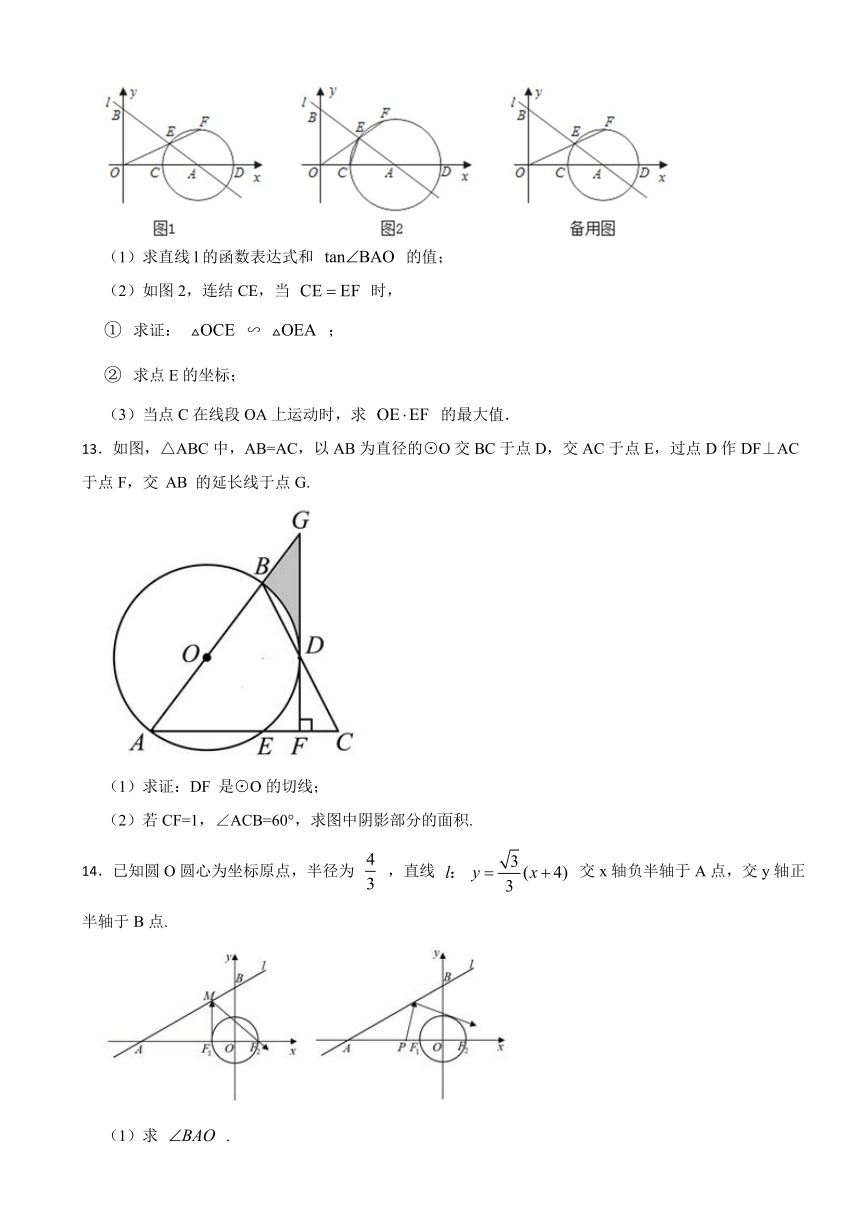
(1)求直线l的函数表达式和 的值;
(2)如图2,连结CE,当 时,
求证: ∽ ;
求点E的坐标;
(3)当点C在线段OA上运动时,求 的最大值.
13.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交 AB 的延长线于点G.
(1)求证:DF 是⊙O的切线;
(2)若CF=1,∠ACB=60°,求图中阴影部分的面积.
14.已知圆O圆心为坐标原点,半径为 ,直线 交x轴负半轴于A点,交y轴正半轴于B点.
(1)求 .
(2)设圆O与x轴的两交点是 ,若从 发出的光线经 上的点M反射后过点 ,求光线从 射出经反射到 经过的路程.
(3)点P是x轴负半轴上一点,从点P发出的光线经 反射后与圆O相切.若光线从射出经反射到相切经过的路程最短,求点P的坐标.
15.已知:△ABC内接于⊙O,连接CO并延长交AB于点E,交⊙O于点D,满足∠BED=3∠ACD.
(1)如图1,求证:AB=AC;
(2)如图2,连接BD,点F为弧BD上一点,连接CF,弧CF=弧BD,过点A作AG⊥CD,垂足为点G,求证:CF+DG=CG;
(3)如图3,在(2)的条件下,点H为AC上一点,分别连接DH、OH,OH⊥DH,过点C作CP⊥AC,交⊙O于点P,OH:CP=1: ,CF=12,连接PF,求PF的长.
16.已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=8,求AC的长.
17.
(1)问题提出
如图1,在 中, , , ,求 的外接圆半径R的值;
(2)问题探究
如图2,在 中, , , ,点D为边BC上的动点,连接AD以AD为直径作 交边AB、AC分别于点E、F,接E、F,求EF的最小值;
(3)问题解决
如图3,在四边形ABCD中, , , , ,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
18.在平面直角坐标系中,对于两个图形X,Y和直线,若在图形X上存在点A,在图形Y上存在点B,使得点A和点B关于直线对称,就称图形X和Y互为m-关联.
(1)若的半径为1,点与为m-关联,则m的值为 ;
(2)已知点,射线与线段为t-关联,求t的取值范围;
(3)已知的半径为2,直线与x轴,y轴分别交于点C,D,若关于对称的图形S与线段CD互为2m-关联,直接写出m的取值范围.
19.已知 是 的直径,点 为 上一点,点 为 的内心, .
(1)如图1,连接 并延长交 于点 ,连接 ,若 ,求证: ;
(2)如图2,点 为 的中点,连接 , ,过点 作 于点 ,若 ,求 的长.
20.对于平面直角坐标系xOy中的图形W1和图形W2.给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M于点N可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系
(1)如图1,点C(1,0),D(-1,0),E(0, ),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
①线段OP的最小值为 ,最大值为 ;线段CP的取值范直范围是 ;
②在点O,点C中,点 与线段DE满足限距关系;
(2)如图2,⊙O的半径为1,直线 (b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;
(3)⊙O的半径为r(r>0),点H,K是⊙O上的两个点,分别以H,K为圆心,1为半径作圆得到⊙H和¤K,若对于任意点H,K,⊙H和⊙K都满足限距关系,直接写出r的取值范围.
答案解析部分
1.【答案】(1)解:∵为的直径,
∴.
∵,
∴.
∴.
∵,
∴.
∴.
(2)解:所求阴影面积==.
2.【答案】(1)证明:如图,连接 ,
∵ ,∴ ,
又∵ ,∴ ,
∴ ,∴ ,
∵ ,∴ ,
又∵ 在圆上( 为半径),∴ 是 的切线
(2)解:由(1)得 ,∴ ,
∴ ,
在 中, ,
∵ ,∴ ,
∴ ,∴
(3)解:如图,连接 ,
∵ 为 的中点,且 ,
∴ 垂直平分 ,∴ ,∴ ,
∵ ,∴ ,
∴
3.【答案】(1)证明:连结OD,
∵DE⊥AD,
∴AE是⊙O的直径,即点O在AE上.
∵AD是角平分线,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO.
∴∠CAD=∠ADO.
∴OD∥AC.
∴∠ODB=∠C=90°.
∴OD⊥BC.
∵点D在⊙O上,
∴BC是⊙O的切线.
(2)解:∵OD∥AC,
∴∠DOB=∠EAF.
∵∠G=∠EAF,
∴∠DOB=∠G.
∴sin∠DOB=sin∠G= .
设BD=4k,则 OD=OE =3k,
在Rt△OBD中,由勾股定理得 ,
解得, , (舍去),
∴3k=6,即OD=6.
∴⊙O的直径为12.
4.【答案】(1)证明:∵OA为直径,
∴∠OCA=90°,
又∵∠BAO=∠OAC,∠BOA=90°,
∴△AOB∽△ACO;
(2)解:过点C作CD⊥x轴,垂足为D,如图:
∵A(4,0),
∴OA=4.
在Rt△OAC中,∠OAC=30°,
∴ ,
在Rt△DAC中,∠DAC=30°,
∴ ,
即点C到x轴的距离为 ;
(3)解:过点C作CD⊥x轴,垂足为D,如图:
∵∠ABO=90°﹣∠BOC,∠COD=90°﹣∠BOC,
∴∠ABO=∠COD,
且∠CDO=∠AOB=90°,
∴△COD∽△ABO,
∴ .
∵直径OA=4为定值,
∴当CD最大,即CD为半径时, 取得最大值,此时CD的最大值为2,
∴ 的最大值为 .
5.【答案】(1)解:①∵正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0),点E(0,4)在y轴上,
∴点E到正方形ABCD边上C点间的距离最大值,EC=5,
即d(点E)的值为5;
②如图1所示:∵d(点E)=5,
∴d(线段EF)的最小值是5,
∴符合题意的点F满足d(点F)≤5,
当d(点F)=5时,BF1=DF2=5,
∴点F1的坐标为(4,0),点F2的坐标为(-4,0),
将点F1的坐标代入y=kx+4得:0=4k+4,
解得:k=-1,
将点F2的坐标代入y=kx+4得:0=-4k+4,
解得:k=1,
∴k=-1或k=1.
∴当d(线段EF)取最小值时,EF1直线y=kx+4中k≤-1,EF2直线y=kx+4中k≥1,
∴当d(线段EF)取最小值时,k的取值范围为:k≤-1或k≥1;
(2)解:⊙T的圆心为T(7,t),半径为1,
当d(⊙T)=11时,如图2所示:
BM=BN=11,OH=7,
∴T1B=T2B=10,BH=OB+OH=1+7=8,
∴T1H= ,T2H= ,
∴t的取值范围为:-6<t<6.
6.【答案】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,
∵OC=OA,
∴∠A=∠ACO,
∴∠A+∠BCO=90°,
∵∠A=∠BCE,
∴∠BCE+∠BCO=90°,
∴∠OCE=90°,
∴CE是⊙O的切线
(2)解:四边形OBCD是菱形,
理由:∵BC=BE,
∴∠E=∠ECB,
∵∠BCO+∠BCE=∠COB+∠E=90°,
∴∠BCO=∠BOC,
∴BC=OB,
∴△BCO是等边三角形,
∴∠AOC=120°,
∵F是AC的中点,
∴AF=CF,
∵OA=OC,
∴∠AOD=∠COD=60°,
∵OD=OC,
∴△COD是等边三角形,
∴CD=OD=OB=BC,
∴四边形OBCD是菱形.
7.【答案】(1)证明:∵ 是半圆 的直径
∴
在 和 中
∴ ,
∴ ;
(2)解:连接 .
∵ ,由(1)知 ,
∴ ,
∵ ,
∴ ,
∴ .
∵ 是半圆 所在圆的切线,
∴ ,
∴ ,
∴ ,
∴ .
∴ .
(3)解:连接OH,
∵H是AC中点,则OH⊥AC,
故H在以AO为直径的圆上运动,
当点 在 点时,点H与点O重合,
当点C在A点时,点H与点A重合,
所以,点 移动的长度是以 为直径的圆的周长一半,
即L= .
8.【答案】(1)证明:如图,连接 ,
∵ 是 的直径,
∴ 。
∴ .
∵
∴ .
∵ ,
∴ ,
∵ ,∴ ,
∴ .
∵ ,
∴ ,∴ ,
又∵ 为 的半径,
∴ 是 的切线;
(2)解:∵ ,
∴
∴ ,
∴ ,
∴ ,
∴ ,
设 ,则 ,
得 ,
在 中,由勾股定理可得: ,
解得: ,
∴
9.【答案】(1)解:∵PA、PB是的切线,AC是的直径,
∴,,
∴,.
∵,
∴,
在中,.
(2)解:∵四边形ACBM内接于,
∴,
又∵,,
∴,
∴,
∵AC为的直径,
∴,,
∴.
又∵,
∴为等边三角形,
∴,
在中,,,,
∴,则,
∴.
10.【答案】(1)证明:如图,延长BD交⊙O于E,
∵BD⊥OC,
∴BE=2BD, =2 ,
∵ =2 ,
∴ = ,
∴AB=BE,
∴AB=2BD;
(2)解:如图,连接OB,
设⊙O 的半径为r,
∵AB=4 ,CD=2,
∴BD=2 ,
在Rt△OBD中,r2=(r﹣2)2+(2 )2,
解得:r=4,
∵sin∠BOC= = ,
∴∠BOC=60°,
∴阴影部分的面积= ﹣ ×2= π﹣2 .
11.【答案】(1)45°或135°
(2)解:如图②所示,
延长AP交圆O于点Q,连接BQ,则 ,
∵
∴∠APB>∠PQB,即∠APB>∠ACB;
(3)解:连接AO,BO,作 的外接圆,即可得到所求的阴影部分;
(4)4;
12.【答案】(1)解: 直线l: 与x轴交于点 ,
, ,
直线l的函数表达式 , , , ,
在 中,
(2)解: 如图2,连接DF,
, , ,
, ,
四边形CEFD是 的圆内接四边形, , ,
, ∽ ,
过点 EM⊥OA于M,由 知, ,
设 ,则 , , , , ,
,由 知, ∽ , ,
,
,
,
,
舍 或 ,
, ,
(3)解:如图,
设 的半径为r,过点O作 于G,
, ,
, ,
,
,
,
,
,
连接FH,
是 直径,
, ,
,
∽ ,
,
,
时, 最大值为 .
13.【答案】(1)证明:如图,连接,
由题意知,
∵
∴是线段的中点
∴是的中位线
∴
∵
∴
∴
又∵是半径
∴DF 是⊙O的切线.
(2)解:∵,
∴,
∴,是等边三角形
∵
∴
∵
∴,
∴,
∴
∵,
∴
∴,即
解得
∵
∴阴影部分的面积为.
14.【答案】(1)解: 直线 交 轴负半轴于 点,交 轴正半轴于 点,
令 ,则 ,
令 ,则 ,
, ,
, ,
在 中, ,
(2)解: 圆 与 轴的两交点是 , ,半径为 ,
,
由对称性可知,点 关于 的对称点 在过点 且倾斜角为 的直线 上,如图1所示:
则 ,
在△ 中, , , ,
△ 为直角三角形,
,
光线从 射出经反射到 经过的路程为:
(3)解:由对称性可知,点 关于 的对称点 在过点 且倾斜角为 的直线 上,
设光线经 上的点 反射后切点为 ,如图2所示:
则 ,
路程最短即为 上点 到切点 的切线长最短,
连接 、 ,
在 中, 是定值,只有 最短时, 长最短,
此时 应为过原点 且与 垂直的直线与 的交点,这一点又与点 关于 对称,
,
点 的坐标为
15.【答案】(1)证明:如图1,设∠BEC=3
∴∠BAC=∠BEC-∠ACD=3 - =2
连接AD,∵∠DAC=90°
∴∠D=90°-
∴∠B=∠D=90°-
∵∠ACB=180°-∠BAC-∠ABC=180°-2 -(90°- )=90°-
∴∠ABC=∠ACB
∴AB=AC
(2)解:如图2,在CD上取一点Z,使CZ=BD
∵BD=CD,∴DB=CF
∵∠DBA=∠DCA,CZ=BD,AB=AC,
∴
∴AD=AZ,∵AG⊥CD,∴DG=GZ
∴CG=CZ+GZ=CF+DG
(3)解:如图3,连接AP,∵∠ACP=90°
∴AP为直径
作PR⊥PC,∴PR=RC,∠ORC=90°;作OK⊥AC,∴∠OKC=90°
∴∠OKC=∠ORC=∠ACP=90°
∴四边形OKCR为矩形
∴RC=OK
∵OH:CP=1:
设OH= ,PC=2a,∴RC=OK=a,sin∠OHK= =
∴∠OHK=45°
∵OH⊥DH,∴∠DHO=90°
∴∠DHA=180°-90°-45°=45°
∵CD为直径,∴∠DAC=90°
∴∠ADH=90°-45°=45°
∴∠DHA=∠ADH,∴AD=AH,∵∠COP=∠AOD
∴AD=PC,∴AH=AD=PC=2a
∴AK=AH+HK=2a+a=3a,在 中
tan∠OAK=
AO= = =
∴sin∠OAK=
∵∠ADG+∠DAG=90°,∴tan∠ACD=tan∠DAG=tan∠OAK=
∴AG=3DG,CG=3AG
∴CG=9DG
由(2)可知,CG=DG+CF,∴DG+12=9DG
∴DG= ,
∴
又∵sin∠F=sin∠OAK,作CT⊥FP,垂足为T
∴sin∠F= =
∴CT=
16.【答案】(1)证明:∵BE=CF,
∴弧BE=弧CF,
∴∠BAE=∠CAF,
∵AF⊥BC,
∴∠ADC=90°,
∴∠FAC+∠ACD=90°,
∵∠E=∠ACD,
∴∠BAE+∠E=90°,
∴∠ABE=90°,
∴ AE是⊙O的直径 .
(2)解:连结OC,
∴∠AOC=2∠ABC,
∵∠ABC=∠CAE,
∴∠AOC=2∠CAE,
∵OA=OA,
∴∠CAO=∠ACO=∠AOC,
∴△AOC为等腰直角三角形,
∵AE=8,
∴AO=CO=4,
∴AC=.
17.【答案】(1)解:如图1中,作 的外接圆,连接OA,OC.
,
又 ,
,
又∵ ,
,
的外接圆的R为6;
(2)解:如图2中,作 于H.
, ,
,
,
当直径AD的值一定时,EF的值也确定,
根据垂线段最短可知当AD与AH重合时,AD的值最短,此时EF的值也最短,
如图 中,当 时,作 于H,连接OE,OF.
, , ,
, ,
,
,
的最小值为12;
(3)解:如图3中,将 绕点A顺时针旋转 得到 ,连接EC,作 交CB的延长线于H,设 .
, ,
, ,
的值最小时,AC的值最小,
,
,
,
,
,
, ,
, ,
,
,
当 时,EC的长最小,
此时 ,
,
的最小值为 .
18.【答案】(1)1.5或0.5
(2)解:如图所示:
设线段l:的左右两个端点分别为,,与轴交于点,
设的解析式为:,
则:,解得:,
∴OA的解析式为:,
设点Q为上的一个动点,在点Q从左到右运动过程中,
在射线上存在一点P,使得P和Q关于直线对称,
当点与点G重合时,为第一个临界位置,此时,
当时,直线上对应点为点H,可得,
在第二个临界位置,点P和点H重合时,此时可得,
综上可知:t的取值范围为;
(3)解:∵直线与x轴,y轴分别交于C,D,
令,则,令,则,
∴,
∴,,
∴,
设关于对称的图形为S,则S的圆心为,半径为2的圆,
圆S与线段互为-关联,如图所示:
若线段CD上存在一点P,圆S上存在一点Q,
则P、Q关于直线对称,
即过圆心的直线是线段的垂直平分线,
∴根据垂径定理,只要圆S与线段CD相交,则交点为点P,
此时在圆S上一定存在一点Q与点P关于直线对称,
当圆S向下运动时,如图所示:
当圆S经过点时,圆S的圆心为,半径为2,
此时,解得:,
圆S在上图基础上继续向上运动,如图所示:
当圆S经过点C时,
∵,
∴点S与点D重合,
此时,解得:,
∴m的取值范围为:;
当圆S从上图位置继续向上运动时,如图所示:
当圆S经过点D时,
∵,
∴为等边三角形,
∴,解得:,
当圆S从上图位置继续向上运动时,如图所示,
当圆S与线段CD相切时,设切点为K,
在中,,,
∴,
解得:,
又∵,
∴,
∴,
解得:,
∴m的取值范围为:;
综上可知,m的取值范围为:或.
19.【答案】(1)证明:∵ 是直径,
∴ .
∵ 是 的内心,
∴ ,
.
∴ .
∴ ,
∵ ,
∴ .
∴ .
∵ ,
∴ ,
∴
(2)解:连接 ,过点 作 于点 ,
∵ 为 的直径,
∴ ,
∵ , ,
∴ ,
∵点 为 的中点,
∴ ,
∵点 是 的内心,
∴点 在 上,
∵ ,
∴ ,GE是 的内切圆半径,
∴ ,
∴ ,
∴ ,
∵点 为 的中点,
∴ ,
∵点 是 的内心,
∴ ,
∴ ,
∴ ,
∴ ,
∵ , ,
∴ ,
∵ ,
∴ ,
∴ .
20.【答案】(1);;;O
(2)解:直线 与x轴、y轴分别交于点F,G(0,b),
当0<b<1时,线段FG在⊙O内部,与⊙O无公共点,
此时⊙O上的点到线段FG的最小距离为1-b,最大距离为1+b,
∵线段FG与⊙O满足限距关系,
∴1+b≥2(1-b),
解得 ,
∴b的取值范围为 .
当1≤b≤2时,线段FG与⊙O有公共点,线段FG与⊙O满足限距关系,
当b>2时,线段FG在⊙O的外部,与⊙O没有公共点,
此时⊙O上的点到线段FG的最小距离为 ,最大距离为b+1,
∵线段FG与⊙O满足限距关系,
∴ ,
而 总成立,
∴b>2时,线段FG 与⊙O满足限距关系,综上所述,b的取值范围为
(3)解:r的取值范围为0<r≤3
1.如图,是的直径,点,在上,,交于点,.
(1)求的度数;
(2)若是的切线,与的延长线交于点,.直接写出图中阴影部分的面积.
2.如图,已知 是 的直径, , 与圆交于点 ,过点 作 于点 ,与 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 半径长为3, ,求 的长;
(3)若 与圆交于点 , 为 的中点, ,求 的度数.
3.如图,在Rt△ 中, , 平分∠ , 交 于点 ,△ 的外接圆⊙ 与边 相交于点 ,过点 作 的垂线交 于 ,交 于 ,交⊙ 于点 ,连接 .
(1)求证:BC是⊙O的切线;
(2)若sin∠G= ,AB=16,求⊙O的直径.
4.如图,在平面直角坐标系中,点A的坐标为(4,0),B是y轴正半轴上的一个动点,以OA为直径作圆,交AB于点C.
(1)求证:△AOB∽△ACO;
(2)当∠OAB=30°时,求点C到x轴的距离;
(3)求 的最大值.
5.在平面直角坐标系xOy中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作d(M).
(1)已知点E(0,4),
①直接写出d(点E)的值;
②直线y=kx+4(k≠0)与x轴交于点F,当d(线段EF)取最小值时,求k的取值范围;
(2)⊙T的圆心为T(7,t),半径为1.若d(⊙T)<11,请直接写出t的取值范围.
6.AB是⊙O的直径,C点在⊙O上,F是AC的中点,OF的延长线交⊙O于点D,点E在AB的延长线上,∠A=∠BCE.
(1)求证:CE是⊙O的切线;
(2)若BC=BE,判定四边形OBCD的形状,并说明理由.
7.如图, 是半圆 的直径, 是半圆 上不同于 、 两点的任意一点, 是半圆 上一动点, 与 相交于点 , 是半圆 所在圆的切线,与 的延长线相交于点 .
(1)若 ,求证: ;
(2)若 , , .求 ;(答案保留 )
(3)若 , 为 的中点,点 从 移动到 时,请直接写出点 移动的长度.(答案保留 )
8.如图, 是 的直径,点 在 的延长线上, 、 是 上的两点,且 ,连接 , .
(1)求证: 是 的切线;
(2)若 , ,求弦 的长.
9.如图,AC是⊙O的直径,PA、PB是⊙O的切线,切点分别是点A、B.
(1)如图1,若∠BAC=25°,求∠P的度数.
(2)如图2,若M是劣弧AB上一点,∠AMB=∠AOB,BC=2,求AP的长.
10.如图,A,B,C是⊙O上三点,其中 =2 ,过点B画BD⊥OC于点D.
(1)求证:AB=2BD;
(2)若AB=4 ,CD=2,求图中阴影部分的面积.
11.如图①,AB是圆O的一条弦,点C是优弧 上一点.
(1)若∠ACB=45°,点P是O上一点(不与A. B重合),则∠APB= ;
(2)如图②,若点P是弦AB与 所围成的弓形区域(不含弦AB与 )内一点.求证:∠APB>∠ACB;
(3)请在图③中直接用阴影部分表示出在弦AB与 所围成的弓形区域内满足
的点P所在的范围;
(4)在(1)的条件下,以PB为边,向右作等腰直角三角形PBQ,连结AQ,如图4,已知AB=2,
①当点Q在线段AB的延长线上时,线段AQ的长为
②线段AQ的最小值为
12.如图1,直线l: 与x轴交于点 ,与y轴交于点B,点C是线段OA上一动点 以点A为圆心,AC长为半径作 交x轴于另一点D,交线段AB于点E,连结OE并延长交 于点F.
(1)求直线l的函数表达式和 的值;
(2)如图2,连结CE,当 时,
求证: ∽ ;
求点E的坐标;
(3)当点C在线段OA上运动时,求 的最大值.
13.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交 AB 的延长线于点G.
(1)求证:DF 是⊙O的切线;
(2)若CF=1,∠ACB=60°,求图中阴影部分的面积.
14.已知圆O圆心为坐标原点,半径为 ,直线 交x轴负半轴于A点,交y轴正半轴于B点.
(1)求 .
(2)设圆O与x轴的两交点是 ,若从 发出的光线经 上的点M反射后过点 ,求光线从 射出经反射到 经过的路程.
(3)点P是x轴负半轴上一点,从点P发出的光线经 反射后与圆O相切.若光线从射出经反射到相切经过的路程最短,求点P的坐标.
15.已知:△ABC内接于⊙O,连接CO并延长交AB于点E,交⊙O于点D,满足∠BED=3∠ACD.
(1)如图1,求证:AB=AC;
(2)如图2,连接BD,点F为弧BD上一点,连接CF,弧CF=弧BD,过点A作AG⊥CD,垂足为点G,求证:CF+DG=CG;
(3)如图3,在(2)的条件下,点H为AC上一点,分别连接DH、OH,OH⊥DH,过点C作CP⊥AC,交⊙O于点P,OH:CP=1: ,CF=12,连接PF,求PF的长.
16.已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=8,求AC的长.
17.
(1)问题提出
如图1,在 中, , , ,求 的外接圆半径R的值;
(2)问题探究
如图2,在 中, , , ,点D为边BC上的动点,连接AD以AD为直径作 交边AB、AC分别于点E、F,接E、F,求EF的最小值;
(3)问题解决
如图3,在四边形ABCD中, , , , ,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
18.在平面直角坐标系中,对于两个图形X,Y和直线,若在图形X上存在点A,在图形Y上存在点B,使得点A和点B关于直线对称,就称图形X和Y互为m-关联.
(1)若的半径为1,点与为m-关联,则m的值为 ;
(2)已知点,射线与线段为t-关联,求t的取值范围;
(3)已知的半径为2,直线与x轴,y轴分别交于点C,D,若关于对称的图形S与线段CD互为2m-关联,直接写出m的取值范围.
19.已知 是 的直径,点 为 上一点,点 为 的内心, .
(1)如图1,连接 并延长交 于点 ,连接 ,若 ,求证: ;
(2)如图2,点 为 的中点,连接 , ,过点 作 于点 ,若 ,求 的长.
20.对于平面直角坐标系xOy中的图形W1和图形W2.给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M于点N可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系
(1)如图1,点C(1,0),D(-1,0),E(0, ),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
①线段OP的最小值为 ,最大值为 ;线段CP的取值范直范围是 ;
②在点O,点C中,点 与线段DE满足限距关系;
(2)如图2,⊙O的半径为1,直线 (b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;
(3)⊙O的半径为r(r>0),点H,K是⊙O上的两个点,分别以H,K为圆心,1为半径作圆得到⊙H和¤K,若对于任意点H,K,⊙H和⊙K都满足限距关系,直接写出r的取值范围.
答案解析部分
1.【答案】(1)解:∵为的直径,
∴.
∵,
∴.
∴.
∵,
∴.
∴.
(2)解:所求阴影面积==.
2.【答案】(1)证明:如图,连接 ,
∵ ,∴ ,
又∵ ,∴ ,
∴ ,∴ ,
∵ ,∴ ,
又∵ 在圆上( 为半径),∴ 是 的切线
(2)解:由(1)得 ,∴ ,
∴ ,
在 中, ,
∵ ,∴ ,
∴ ,∴
(3)解:如图,连接 ,
∵ 为 的中点,且 ,
∴ 垂直平分 ,∴ ,∴ ,
∵ ,∴ ,
∴
3.【答案】(1)证明:连结OD,
∵DE⊥AD,
∴AE是⊙O的直径,即点O在AE上.
∵AD是角平分线,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO.
∴∠CAD=∠ADO.
∴OD∥AC.
∴∠ODB=∠C=90°.
∴OD⊥BC.
∵点D在⊙O上,
∴BC是⊙O的切线.
(2)解:∵OD∥AC,
∴∠DOB=∠EAF.
∵∠G=∠EAF,
∴∠DOB=∠G.
∴sin∠DOB=sin∠G= .
设BD=4k,则 OD=OE =3k,
在Rt△OBD中,由勾股定理得 ,
解得, , (舍去),
∴3k=6,即OD=6.
∴⊙O的直径为12.
4.【答案】(1)证明:∵OA为直径,
∴∠OCA=90°,
又∵∠BAO=∠OAC,∠BOA=90°,
∴△AOB∽△ACO;
(2)解:过点C作CD⊥x轴,垂足为D,如图:
∵A(4,0),
∴OA=4.
在Rt△OAC中,∠OAC=30°,
∴ ,
在Rt△DAC中,∠DAC=30°,
∴ ,
即点C到x轴的距离为 ;
(3)解:过点C作CD⊥x轴,垂足为D,如图:
∵∠ABO=90°﹣∠BOC,∠COD=90°﹣∠BOC,
∴∠ABO=∠COD,
且∠CDO=∠AOB=90°,
∴△COD∽△ABO,
∴ .
∵直径OA=4为定值,
∴当CD最大,即CD为半径时, 取得最大值,此时CD的最大值为2,
∴ 的最大值为 .
5.【答案】(1)解:①∵正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0),点E(0,4)在y轴上,
∴点E到正方形ABCD边上C点间的距离最大值,EC=5,
即d(点E)的值为5;
②如图1所示:∵d(点E)=5,
∴d(线段EF)的最小值是5,
∴符合题意的点F满足d(点F)≤5,
当d(点F)=5时,BF1=DF2=5,
∴点F1的坐标为(4,0),点F2的坐标为(-4,0),
将点F1的坐标代入y=kx+4得:0=4k+4,
解得:k=-1,
将点F2的坐标代入y=kx+4得:0=-4k+4,
解得:k=1,
∴k=-1或k=1.
∴当d(线段EF)取最小值时,EF1直线y=kx+4中k≤-1,EF2直线y=kx+4中k≥1,
∴当d(线段EF)取最小值时,k的取值范围为:k≤-1或k≥1;
(2)解:⊙T的圆心为T(7,t),半径为1,
当d(⊙T)=11时,如图2所示:
BM=BN=11,OH=7,
∴T1B=T2B=10,BH=OB+OH=1+7=8,
∴T1H= ,T2H= ,
∴t的取值范围为:-6<t<6.
6.【答案】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,
∵OC=OA,
∴∠A=∠ACO,
∴∠A+∠BCO=90°,
∵∠A=∠BCE,
∴∠BCE+∠BCO=90°,
∴∠OCE=90°,
∴CE是⊙O的切线
(2)解:四边形OBCD是菱形,
理由:∵BC=BE,
∴∠E=∠ECB,
∵∠BCO+∠BCE=∠COB+∠E=90°,
∴∠BCO=∠BOC,
∴BC=OB,
∴△BCO是等边三角形,
∴∠AOC=120°,
∵F是AC的中点,
∴AF=CF,
∵OA=OC,
∴∠AOD=∠COD=60°,
∵OD=OC,
∴△COD是等边三角形,
∴CD=OD=OB=BC,
∴四边形OBCD是菱形.
7.【答案】(1)证明:∵ 是半圆 的直径
∴
在 和 中
∴ ,
∴ ;
(2)解:连接 .
∵ ,由(1)知 ,
∴ ,
∵ ,
∴ ,
∴ .
∵ 是半圆 所在圆的切线,
∴ ,
∴ ,
∴ ,
∴ .
∴ .
(3)解:连接OH,
∵H是AC中点,则OH⊥AC,
故H在以AO为直径的圆上运动,
当点 在 点时,点H与点O重合,
当点C在A点时,点H与点A重合,
所以,点 移动的长度是以 为直径的圆的周长一半,
即L= .
8.【答案】(1)证明:如图,连接 ,
∵ 是 的直径,
∴ 。
∴ .
∵
∴ .
∵ ,
∴ ,
∵ ,∴ ,
∴ .
∵ ,
∴ ,∴ ,
又∵ 为 的半径,
∴ 是 的切线;
(2)解:∵ ,
∴
∴ ,
∴ ,
∴ ,
∴ ,
设 ,则 ,
得 ,
在 中,由勾股定理可得: ,
解得: ,
∴
9.【答案】(1)解:∵PA、PB是的切线,AC是的直径,
∴,,
∴,.
∵,
∴,
在中,.
(2)解:∵四边形ACBM内接于,
∴,
又∵,,
∴,
∴,
∵AC为的直径,
∴,,
∴.
又∵,
∴为等边三角形,
∴,
在中,,,,
∴,则,
∴.
10.【答案】(1)证明:如图,延长BD交⊙O于E,
∵BD⊥OC,
∴BE=2BD, =2 ,
∵ =2 ,
∴ = ,
∴AB=BE,
∴AB=2BD;
(2)解:如图,连接OB,
设⊙O 的半径为r,
∵AB=4 ,CD=2,
∴BD=2 ,
在Rt△OBD中,r2=(r﹣2)2+(2 )2,
解得:r=4,
∵sin∠BOC= = ,
∴∠BOC=60°,
∴阴影部分的面积= ﹣ ×2= π﹣2 .
11.【答案】(1)45°或135°
(2)解:如图②所示,
延长AP交圆O于点Q,连接BQ,则 ,
∵
∴∠APB>∠PQB,即∠APB>∠ACB;
(3)解:连接AO,BO,作 的外接圆,即可得到所求的阴影部分;
(4)4;
12.【答案】(1)解: 直线l: 与x轴交于点 ,
, ,
直线l的函数表达式 , , , ,
在 中,
(2)解: 如图2,连接DF,
, , ,
, ,
四边形CEFD是 的圆内接四边形, , ,
, ∽ ,
过点 EM⊥OA于M,由 知, ,
设 ,则 , , , , ,
,由 知, ∽ , ,
,
,
,
,
舍 或 ,
, ,
(3)解:如图,
设 的半径为r,过点O作 于G,
, ,
, ,
,
,
,
,
,
连接FH,
是 直径,
, ,
,
∽ ,
,
,
时, 最大值为 .
13.【答案】(1)证明:如图,连接,
由题意知,
∵
∴是线段的中点
∴是的中位线
∴
∵
∴
∴
又∵是半径
∴DF 是⊙O的切线.
(2)解:∵,
∴,
∴,是等边三角形
∵
∴
∵
∴,
∴,
∴
∵,
∴
∴,即
解得
∵
∴阴影部分的面积为.
14.【答案】(1)解: 直线 交 轴负半轴于 点,交 轴正半轴于 点,
令 ,则 ,
令 ,则 ,
, ,
, ,
在 中, ,
(2)解: 圆 与 轴的两交点是 , ,半径为 ,
,
由对称性可知,点 关于 的对称点 在过点 且倾斜角为 的直线 上,如图1所示:
则 ,
在△ 中, , , ,
△ 为直角三角形,
,
光线从 射出经反射到 经过的路程为:
(3)解:由对称性可知,点 关于 的对称点 在过点 且倾斜角为 的直线 上,
设光线经 上的点 反射后切点为 ,如图2所示:
则 ,
路程最短即为 上点 到切点 的切线长最短,
连接 、 ,
在 中, 是定值,只有 最短时, 长最短,
此时 应为过原点 且与 垂直的直线与 的交点,这一点又与点 关于 对称,
,
点 的坐标为
15.【答案】(1)证明:如图1,设∠BEC=3
∴∠BAC=∠BEC-∠ACD=3 - =2
连接AD,∵∠DAC=90°
∴∠D=90°-
∴∠B=∠D=90°-
∵∠ACB=180°-∠BAC-∠ABC=180°-2 -(90°- )=90°-
∴∠ABC=∠ACB
∴AB=AC
(2)解:如图2,在CD上取一点Z,使CZ=BD
∵BD=CD,∴DB=CF
∵∠DBA=∠DCA,CZ=BD,AB=AC,
∴
∴AD=AZ,∵AG⊥CD,∴DG=GZ
∴CG=CZ+GZ=CF+DG
(3)解:如图3,连接AP,∵∠ACP=90°
∴AP为直径
作PR⊥PC,∴PR=RC,∠ORC=90°;作OK⊥AC,∴∠OKC=90°
∴∠OKC=∠ORC=∠ACP=90°
∴四边形OKCR为矩形
∴RC=OK
∵OH:CP=1:
设OH= ,PC=2a,∴RC=OK=a,sin∠OHK= =
∴∠OHK=45°
∵OH⊥DH,∴∠DHO=90°
∴∠DHA=180°-90°-45°=45°
∵CD为直径,∴∠DAC=90°
∴∠ADH=90°-45°=45°
∴∠DHA=∠ADH,∴AD=AH,∵∠COP=∠AOD
∴AD=PC,∴AH=AD=PC=2a
∴AK=AH+HK=2a+a=3a,在 中
tan∠OAK=
AO= = =
∴sin∠OAK=
∵∠ADG+∠DAG=90°,∴tan∠ACD=tan∠DAG=tan∠OAK=
∴AG=3DG,CG=3AG
∴CG=9DG
由(2)可知,CG=DG+CF,∴DG+12=9DG
∴DG= ,
∴
又∵sin∠F=sin∠OAK,作CT⊥FP,垂足为T
∴sin∠F= =
∴CT=
16.【答案】(1)证明:∵BE=CF,
∴弧BE=弧CF,
∴∠BAE=∠CAF,
∵AF⊥BC,
∴∠ADC=90°,
∴∠FAC+∠ACD=90°,
∵∠E=∠ACD,
∴∠BAE+∠E=90°,
∴∠ABE=90°,
∴ AE是⊙O的直径 .
(2)解:连结OC,
∴∠AOC=2∠ABC,
∵∠ABC=∠CAE,
∴∠AOC=2∠CAE,
∵OA=OA,
∴∠CAO=∠ACO=∠AOC,
∴△AOC为等腰直角三角形,
∵AE=8,
∴AO=CO=4,
∴AC=.
17.【答案】(1)解:如图1中,作 的外接圆,连接OA,OC.
,
又 ,
,
又∵ ,
,
的外接圆的R为6;
(2)解:如图2中,作 于H.
, ,
,
,
当直径AD的值一定时,EF的值也确定,
根据垂线段最短可知当AD与AH重合时,AD的值最短,此时EF的值也最短,
如图 中,当 时,作 于H,连接OE,OF.
, , ,
, ,
,
,
的最小值为12;
(3)解:如图3中,将 绕点A顺时针旋转 得到 ,连接EC,作 交CB的延长线于H,设 .
, ,
, ,
的值最小时,AC的值最小,
,
,
,
,
,
, ,
, ,
,
,
当 时,EC的长最小,
此时 ,
,
的最小值为 .
18.【答案】(1)1.5或0.5
(2)解:如图所示:
设线段l:的左右两个端点分别为,,与轴交于点,
设的解析式为:,
则:,解得:,
∴OA的解析式为:,
设点Q为上的一个动点,在点Q从左到右运动过程中,
在射线上存在一点P,使得P和Q关于直线对称,
当点与点G重合时,为第一个临界位置,此时,
当时,直线上对应点为点H,可得,
在第二个临界位置,点P和点H重合时,此时可得,
综上可知:t的取值范围为;
(3)解:∵直线与x轴,y轴分别交于C,D,
令,则,令,则,
∴,
∴,,
∴,
设关于对称的图形为S,则S的圆心为,半径为2的圆,
圆S与线段互为-关联,如图所示:
若线段CD上存在一点P,圆S上存在一点Q,
则P、Q关于直线对称,
即过圆心的直线是线段的垂直平分线,
∴根据垂径定理,只要圆S与线段CD相交,则交点为点P,
此时在圆S上一定存在一点Q与点P关于直线对称,
当圆S向下运动时,如图所示:
当圆S经过点时,圆S的圆心为,半径为2,
此时,解得:,
圆S在上图基础上继续向上运动,如图所示:
当圆S经过点C时,
∵,
∴点S与点D重合,
此时,解得:,
∴m的取值范围为:;
当圆S从上图位置继续向上运动时,如图所示:
当圆S经过点D时,
∵,
∴为等边三角形,
∴,解得:,
当圆S从上图位置继续向上运动时,如图所示,
当圆S与线段CD相切时,设切点为K,
在中,,,
∴,
解得:,
又∵,
∴,
∴,
解得:,
∴m的取值范围为:;
综上可知,m的取值范围为:或.
19.【答案】(1)证明:∵ 是直径,
∴ .
∵ 是 的内心,
∴ ,
.
∴ .
∴ ,
∵ ,
∴ .
∴ .
∵ ,
∴ ,
∴
(2)解:连接 ,过点 作 于点 ,
∵ 为 的直径,
∴ ,
∵ , ,
∴ ,
∵点 为 的中点,
∴ ,
∵点 是 的内心,
∴点 在 上,
∵ ,
∴ ,GE是 的内切圆半径,
∴ ,
∴ ,
∴ ,
∵点 为 的中点,
∴ ,
∵点 是 的内心,
∴ ,
∴ ,
∴ ,
∴ ,
∵ , ,
∴ ,
∵ ,
∴ ,
∴ .
20.【答案】(1);;;O
(2)解:直线 与x轴、y轴分别交于点F,G(0,b),
当0<b<1时,线段FG在⊙O内部,与⊙O无公共点,
此时⊙O上的点到线段FG的最小距离为1-b,最大距离为1+b,
∵线段FG与⊙O满足限距关系,
∴1+b≥2(1-b),
解得 ,
∴b的取值范围为 .
当1≤b≤2时,线段FG与⊙O有公共点,线段FG与⊙O满足限距关系,
当b>2时,线段FG在⊙O的外部,与⊙O没有公共点,
此时⊙O上的点到线段FG的最小距离为 ,最大距离为b+1,
∵线段FG与⊙O满足限距关系,
∴ ,
而 总成立,
∴b>2时,线段FG 与⊙O满足限距关系,综上所述,b的取值范围为
(3)解:r的取值范围为0<r≤3
同课章节目录
