图形的相似(第2课时)
图片预览








文档简介
课件28张PPT。27.1相似多边形的性质1、2 × =____
2、点(2,-3)关于原点对称的坐标是____
3、如果 = ,则x=___
4、在⊙o中,∠AOC=130°,
∠ABC= ___
6(-2,3)1565°教学目标1.知道相似多边形的主要特征,即:相似多边形的对应角相等,对应边的比相等.
2.会根据相似多边形的特征识别两个多边形是否相似,并会运用其性质进行相关的计算.
教学重点:相似多边形的主要特征与识别.
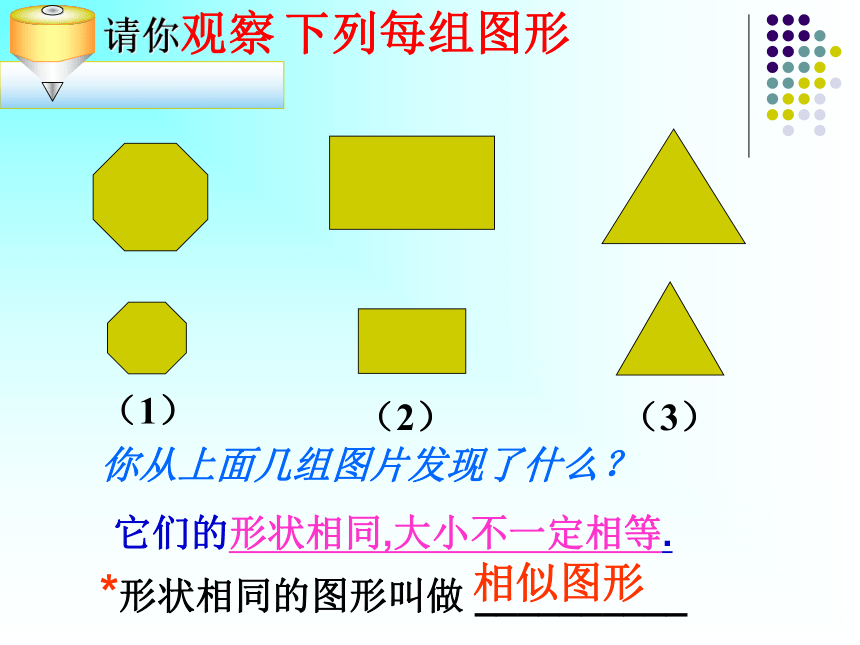
教学难点:运用相似多边形的特征进行相关 的计算.黄山松非洲象天坛下列每组图形(1)(2)(3)你从上面几组图片发现了什么?它们的形状相同,大小不一定相等. 两个相似的平面图形之间有什么关系呢?相似图形有什么主要特征呢?猜一猜如果两个图形相似,它们的对应边、对应角可能存在某种关系.思考1、图27.1-4(1)中的△A1B1C1是由正△ ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
ABCA1B1C1思考 ∠A__∠A1
∠B__∠B1
∠C__∠C1
由 AB =BC=AC
A1B1 =B1 C1 =A1 C1
===ABCA1B1C12223331、图27.1-4(1)中的△A1B1C1是由正△ ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
对于四条线段a、b、c、d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 = (即ad=bc),我们就说这四条线段是成比例线段,简称比例线段像上面的式子:例如:如果四条线段a=1, b=3, c=2, d=6,那么这四条线段是否成比例线段?2、对于图27.1-4(2)中两个相似的正六边形,你是否也能得到类似的结论? 探究 图27.1-5(1)是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?
ABCDEF 对于图27.1-5(2)中两个相似的四边形,
它们的对应角、对应边是否有同样的结论?讨论总结:相似多边形的性质相似多边形对应角相等,对应边的比相等.
我们把相似多边形对应边的比称为相似比相似比为1时,相似的两个图形有什么关系?
反过来,怎样的两个多边形是相似多边形?如果两个多边形满足对应角相等,
对应边的比相等,那么这两个多边形相似。填空:
(1)若△ABC和△ A1B1C1相似,且∠A=50°, ∠B=60°,则∠C1= ______
(2)如图△ABC和△ A1B1C1相似,则 ∠B1 =______,它们的相似比为( ).70 ° 35°口答:
(3)如图所示的两个五边形是否相似?例题:如图,四边形ABCD和EFGH相似,求∠α、∠β的大小和EH的长度x. 解:∵四边形ABCD和EFGH相似
∴ ∠α= ∠ C= 83°, ∠ A= ∠E=118 °
∴在四边形ABCD中,
∠ β=360 °-( 78°+ 83°+ 118 °)=81 °
∴ = ,即 = 解得:X=28(cm)我思,我进步A B D F巩固训练练习:
⑴如图1,两个四边形相似,则x= ,
y = ∠α= ;
⑵如图2,两个矩形相似,则x= .2.5 1.5 90022.5 ABCDEFGH2、如图所示的两个三角形相似吗?为什么?5510101、我知道了……
2、我学会了……
3、我发现了……
中考连接1、(2008年大连)如图若△ABC和△DEF相似,则∠D的度数为______。30°2、(2004年南京)在比例尺是1:8000的南京市城区地图上,太平南路的长度月约为25cm,它的实际长度约为( )A 320cmB 320mC 2000cmD 2000mD如图,点E、F分别是矩形ABCD的边AD、 BC的中点,若矩形ABCD与矩形EABF相似, AB=1,求矩形ABCD的面积.提 高 练 习课本P40练习第1题和第3题谢谢指导!
2、点(2,-3)关于原点对称的坐标是____
3、如果 = ,则x=___
4、在⊙o中,∠AOC=130°,
∠ABC= ___
6(-2,3)1565°教学目标1.知道相似多边形的主要特征,即:相似多边形的对应角相等,对应边的比相等.
2.会根据相似多边形的特征识别两个多边形是否相似,并会运用其性质进行相关的计算.
教学重点:相似多边形的主要特征与识别.
教学难点:运用相似多边形的特征进行相关 的计算.黄山松非洲象天坛下列每组图形(1)(2)(3)你从上面几组图片发现了什么?它们的形状相同,大小不一定相等. 两个相似的平面图形之间有什么关系呢?相似图形有什么主要特征呢?猜一猜如果两个图形相似,它们的对应边、对应角可能存在某种关系.思考1、图27.1-4(1)中的△A1B1C1是由正△ ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
ABCA1B1C1思考 ∠A__∠A1
∠B__∠B1
∠C__∠C1
由 AB =BC=AC
A1B1 =B1 C1 =A1 C1
===ABCA1B1C12223331、图27.1-4(1)中的△A1B1C1是由正△ ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
对于四条线段a、b、c、d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 = (即ad=bc),我们就说这四条线段是成比例线段,简称比例线段像上面的式子:例如:如果四条线段a=1, b=3, c=2, d=6,那么这四条线段是否成比例线段?2、对于图27.1-4(2)中两个相似的正六边形,你是否也能得到类似的结论? 探究 图27.1-5(1)是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?
ABCDEF 对于图27.1-5(2)中两个相似的四边形,
它们的对应角、对应边是否有同样的结论?讨论总结:相似多边形的性质相似多边形对应角相等,对应边的比相等.
我们把相似多边形对应边的比称为相似比相似比为1时,相似的两个图形有什么关系?
反过来,怎样的两个多边形是相似多边形?如果两个多边形满足对应角相等,
对应边的比相等,那么这两个多边形相似。填空:
(1)若△ABC和△ A1B1C1相似,且∠A=50°, ∠B=60°,则∠C1= ______
(2)如图△ABC和△ A1B1C1相似,则 ∠B1 =______,它们的相似比为( ).70 ° 35°口答:
(3)如图所示的两个五边形是否相似?例题:如图,四边形ABCD和EFGH相似,求∠α、∠β的大小和EH的长度x. 解:∵四边形ABCD和EFGH相似
∴ ∠α= ∠ C= 83°, ∠ A= ∠E=118 °
∴在四边形ABCD中,
∠ β=360 °-( 78°+ 83°+ 118 °)=81 °
∴ = ,即 = 解得:X=28(cm)我思,我进步A B D F巩固训练练习:
⑴如图1,两个四边形相似,则x= ,
y = ∠α= ;
⑵如图2,两个矩形相似,则x= .2.5 1.5 90022.5 ABCDEFGH2、如图所示的两个三角形相似吗?为什么?5510101、我知道了……
2、我学会了……
3、我发现了……
中考连接1、(2008年大连)如图若△ABC和△DEF相似,则∠D的度数为______。30°2、(2004年南京)在比例尺是1:8000的南京市城区地图上,太平南路的长度月约为25cm,它的实际长度约为( )A 320cmB 320mC 2000cmD 2000mD如图,点E、F分别是矩形ABCD的边AD、 BC的中点,若矩形ABCD与矩形EABF相似, AB=1,求矩形ABCD的面积.提 高 练 习课本P40练习第1题和第3题谢谢指导!
