人教版数学八年级下册同步练习17.1.2 勾股定理的实际应用(含答案)
文档属性
| 名称 | 人教版数学八年级下册同步练习17.1.2 勾股定理的实际应用(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 291.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 13:34:20 | ||
图片预览

文档简介
第十七章 勾股定理
17.1 勾股定理
第2课时 勾股定理的实际应用
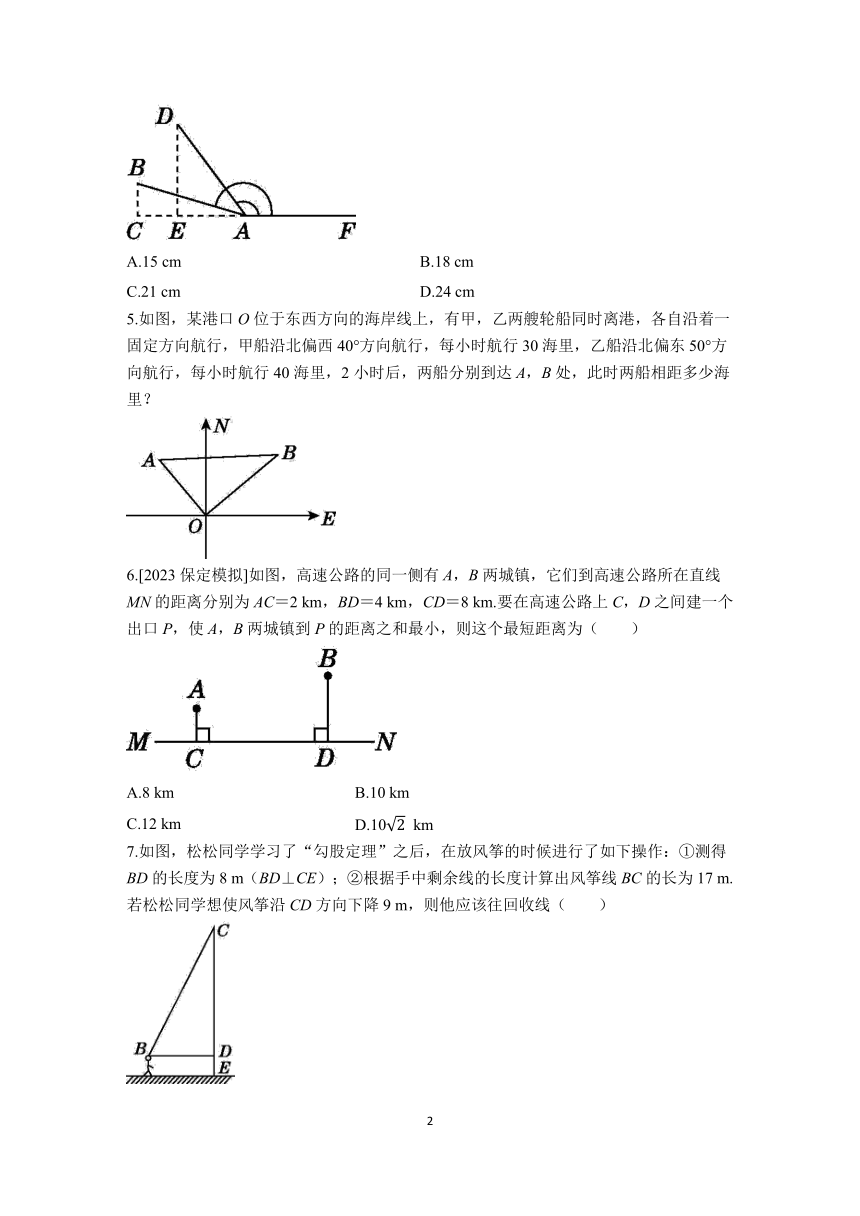
1.如图,湖的两岸有A,B两点,在与AB垂直的BC方向上的点C处测得AC=50米,BC=30米,则A,B两点间的距离为( )
A.40米 B.30米
C.50米 D.10米
2.如图,梯子AB斜靠在一竖直的墙AO上,这时BO为7 m.如果梯子的顶端A沿墙下滑4 m,那么梯子底端B外移8 m,则梯子AB的长为( )
A.24 m B.25 m
C.15 m D.20 m
3.《九章算术》是我国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:今有竹高一丈,末折抵地,去根五尺,问折高者几何?意思是一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部5尺远,则折断处离地面的高度是( )
A.5尺 B.6.25尺 C.4.75尺 D.3.75尺
4.某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF时,顶部边缘B处离桌面的高度BC为7 cm,此时底部边缘A处与C处间的距离AC为24 cm,小组成员调整张角的大小继续探究,最后发现当张角为∠DAF时(D是B的对应点),顶部边缘D处到桌面的距离DE为20 cm,则底部边缘A处与E处间的距离AE为( )
A.15 cm B.18 cm
C.21 cm D.24 cm
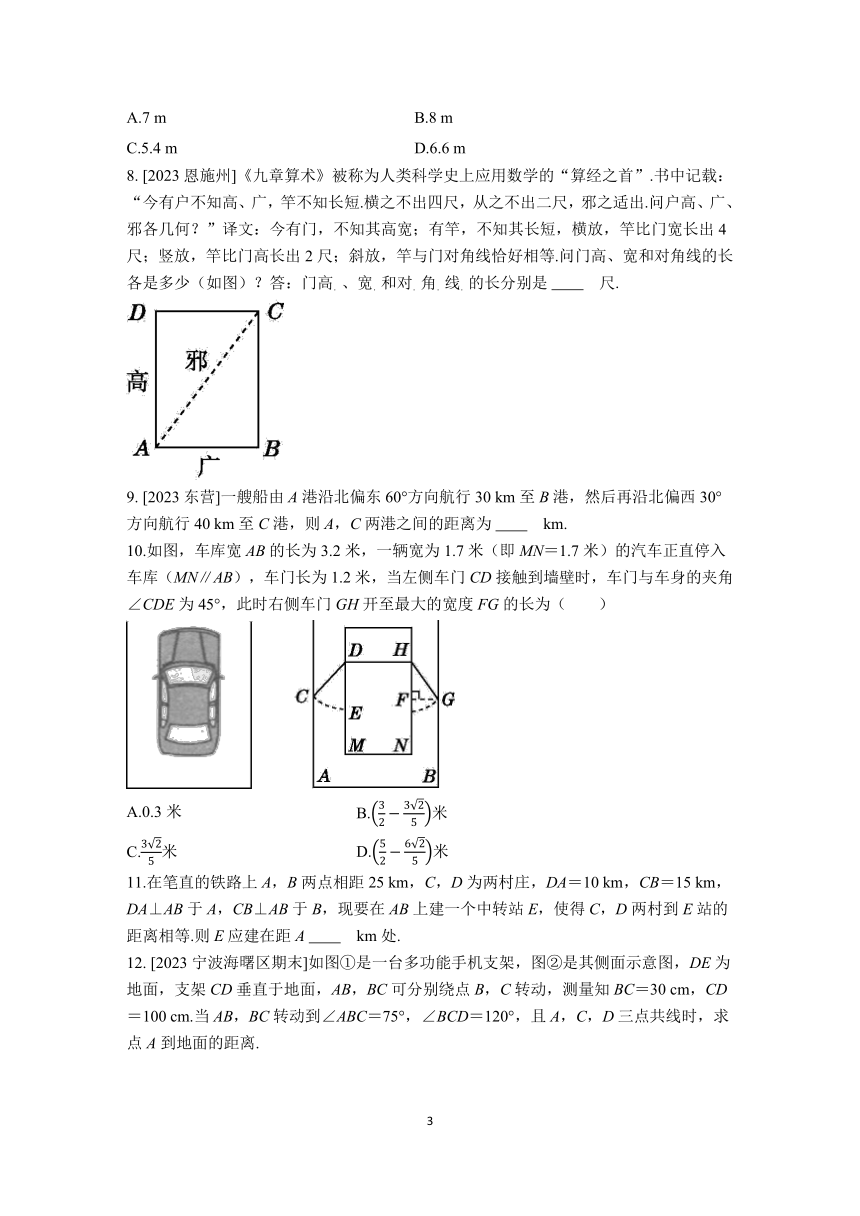
5.如图,某港口O位于东西方向的海岸线上,有甲,乙两艘轮船同时离港,各自沿着一固定方向航行,甲船沿北偏西40°方向航行,每小时航行30海里,乙船沿北偏东50°方向航行,每小时航行40海里,2小时后,两船分别到达A,B处,此时两船相距多少海里?
6.[2023保定模拟]如图,高速公路的同一侧有A,B两城镇,它们到高速公路所在直线MN的距离分别为AC=2 km,BD=4 km,CD=8 km.要在高速公路上C,D之间建一个出口P,使A,B两城镇到P的距离之和最小,则这个最短距离为( )
A.8 km B.10 km
C.12 km D.10 km
7.如图,松松同学学习了“勾股定理”之后,在放风筝的时候进行了如下操作:①测得BD的长度为8 m(BD⊥CE);②根据手中剩余线的长度计算出风筝线BC的长为17 m.若松松同学想使风筝沿CD方向下降9 m,则他应该往回收线( )
A.7 m B.8 m
C.5.4 m D.6.6 m
8. [2023恩施州]《九章算术》被称为人类科学史上应用数学的“算经之首”.书中记载:“今有户不知高、广,竿不知长短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?”译文:今有门,不知其高宽;有竿,不知其长短,横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽和对角线的长各是多少(如图)?答:门高.、宽.和对.角.线.的长分别是 尺.
9. [2023东营]一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
10.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( )
A.0.3米 B.米
C.米 D.米
11.在笔直的铁路上A,B两点相距25 km,C,D为两村庄,DA=10 km,CB=15 km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C,D两村到E站的距离相等.则E应建在距A km处.
12. [2023宁波海曙区期末]如图①是一台多功能手机支架,图②是其侧面示意图,DE为地面,支架CD垂直于地面,AB,BC可分别绕点B,C转动,测量知BC=30 cm,CD=100 cm.当AB,BC转动到∠ABC=75°,∠BCD=120°,且A,C,D三点共线时,求点A到地面的距离.
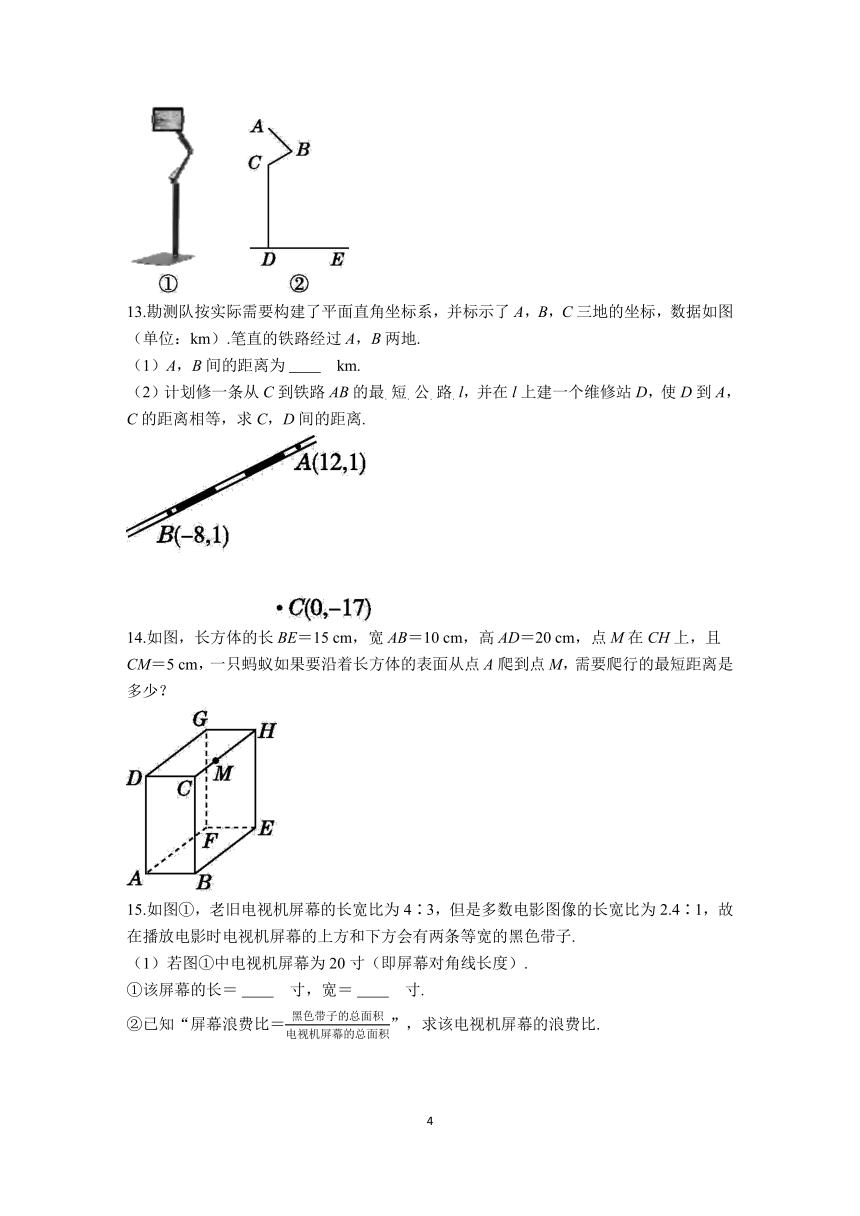
13.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直的铁路经过A,B两地.
(1)A,B间的距离为 km.
(2)计划修一条从C到铁路AB的最.短.公.路.l,并在l上建一个维修站D,使D到A,C的距离相等,求C,D间的距离.
14.如图,长方体的长BE=15 cm,宽AB=10 cm,高AD=20 cm,点M在CH上,且CM=5 cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
15.如图①,老旧电视机屏幕的长宽比为4∶3,但是多数电影图像的长宽比为2.4∶1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度).
①该屏幕的长= 寸,宽= 寸.
②已知“屏幕浪费比=”,求该电视机屏幕的浪费比.
(2)为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(长方形ABCD)恰好包含面积相等且长宽比分别为4∶3的屏幕(长方形EFGH)与2.4∶1的屏幕(长方形MNPQ).求这种屏幕长宽的比值(参考数据:≈2.2,结果精确到0.1).
16.如图,某小区有两个喷泉A,B,两个喷泉的距离AB的长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120 m,BM的长为150 m.求供水点M到喷泉A,B需要铺设的管道总长.
1
参考答案
1.A 2.B 3.D 4.A
5.解:由题意得,∠NOA=40°,∠NOB=50°,OA=60海里,OB=80海里,
∴∠AOB=90°,
∴AB==100(海里),
∴此时两船相距100海里.
6.B
7.A 点拨:∵BD⊥CE,∴∠BDC=90°.
在Rt△CDB中,由勾股定理得:CD===15(m),
设风筝沿CD方向下降9 m至点M,连接BM,如图,
则CM=9 m,∴DM=CD-CM=15-9=6(m),
∴BM===10(m),
∴BC-BM=17-10=7(m),即松松同学应该往回收线7 m.
故选A.
8.8,6,10
9.50
10.B 点拨:过点C作CO⊥DM于O,∴∠COD=90°,∴CO2+DO2=CD2.∵∠CDE=45°,∴∠DCO=45°=∠CDE,
∴CO=DO.∴2CO2=CD2=1.22,∴CO=(米).
易知AB=MN+CO+FG,
∴FG=3.2-1.7-=(米),故选B.
11.15
12.解:连接AC,作BF⊥AC于F,
∵∠BCD=120°,A,C,D三点共线,
∴∠ACB=180°-∠BCD=60°,
∴∠CBF=30°,
∴CF=BC=15 cm,
∴BF==15 cm.
∵∠ABC=75°,
∴∠ABF=∠ABC-∠CBF=45°,
∴∠BAC=45°=∠ABF,
∴AF=BF=15 cm,
∴AD=AF+CF+CD=(115+15)cm.
即点A到地面的距离为(115+15)cm.
13.解:(1)20
(2)如图,过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交l于点D,连接AD.
易知CE=1-(-17)=18 (km),AE=12 km.
设CD=x km,则AD=CD=x km.
由勾股定理得x2=(18-x)2+122,解得x=13.
故CD=13 km.
14.解:分三种情况比较最短距离:
如图①所示,连接AM,AM==5(cm);
如图②所示,连接AM,AM==25(cm);
如图③所示,连接AM,AM==5(cm).
∵5cm>5cm>25 cm,
∴需要爬行的最短距离是25 cm.
15.解:(1)①16;12
②设在该屏幕上播放长宽比为2.4∶1的视频时,视频的宽为a寸.
∴16∶a=2.4∶1,解得a=.
∴黑色带子的宽的和=12-=(寸).
∴屏幕浪费比==.
(2)由题意得=,=,∴PQ=BC,FG=EF.
∵S长方形EFGH=S长方形MNPQ,
∴BC·BC=EF·EF.
∴=,
∴=≈1.8.
答:这种屏幕长宽的比值约为1.8.
16.解:由题意得,AB=250 m,MN⊥AB,MN=120 m,BM=150 m.
在Rt△MNB中,BN===90(m),
∴AN=AB-BN=250-90=160(m),
在Rt△AMN中,AM===200(m),
∴供水点M到喷泉A,B需要铺设的管道总长=200+150=350(m).
17.1 勾股定理
第2课时 勾股定理的实际应用
1.如图,湖的两岸有A,B两点,在与AB垂直的BC方向上的点C处测得AC=50米,BC=30米,则A,B两点间的距离为( )
A.40米 B.30米
C.50米 D.10米
2.如图,梯子AB斜靠在一竖直的墙AO上,这时BO为7 m.如果梯子的顶端A沿墙下滑4 m,那么梯子底端B外移8 m,则梯子AB的长为( )
A.24 m B.25 m
C.15 m D.20 m
3.《九章算术》是我国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:今有竹高一丈,末折抵地,去根五尺,问折高者几何?意思是一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部5尺远,则折断处离地面的高度是( )
A.5尺 B.6.25尺 C.4.75尺 D.3.75尺
4.某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF时,顶部边缘B处离桌面的高度BC为7 cm,此时底部边缘A处与C处间的距离AC为24 cm,小组成员调整张角的大小继续探究,最后发现当张角为∠DAF时(D是B的对应点),顶部边缘D处到桌面的距离DE为20 cm,则底部边缘A处与E处间的距离AE为( )
A.15 cm B.18 cm
C.21 cm D.24 cm
5.如图,某港口O位于东西方向的海岸线上,有甲,乙两艘轮船同时离港,各自沿着一固定方向航行,甲船沿北偏西40°方向航行,每小时航行30海里,乙船沿北偏东50°方向航行,每小时航行40海里,2小时后,两船分别到达A,B处,此时两船相距多少海里?
6.[2023保定模拟]如图,高速公路的同一侧有A,B两城镇,它们到高速公路所在直线MN的距离分别为AC=2 km,BD=4 km,CD=8 km.要在高速公路上C,D之间建一个出口P,使A,B两城镇到P的距离之和最小,则这个最短距离为( )
A.8 km B.10 km
C.12 km D.10 km
7.如图,松松同学学习了“勾股定理”之后,在放风筝的时候进行了如下操作:①测得BD的长度为8 m(BD⊥CE);②根据手中剩余线的长度计算出风筝线BC的长为17 m.若松松同学想使风筝沿CD方向下降9 m,则他应该往回收线( )
A.7 m B.8 m
C.5.4 m D.6.6 m
8. [2023恩施州]《九章算术》被称为人类科学史上应用数学的“算经之首”.书中记载:“今有户不知高、广,竿不知长短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?”译文:今有门,不知其高宽;有竿,不知其长短,横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽和对角线的长各是多少(如图)?答:门高.、宽.和对.角.线.的长分别是 尺.
9. [2023东营]一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
10.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( )
A.0.3米 B.米
C.米 D.米
11.在笔直的铁路上A,B两点相距25 km,C,D为两村庄,DA=10 km,CB=15 km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C,D两村到E站的距离相等.则E应建在距A km处.
12. [2023宁波海曙区期末]如图①是一台多功能手机支架,图②是其侧面示意图,DE为地面,支架CD垂直于地面,AB,BC可分别绕点B,C转动,测量知BC=30 cm,CD=100 cm.当AB,BC转动到∠ABC=75°,∠BCD=120°,且A,C,D三点共线时,求点A到地面的距离.
13.勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直的铁路经过A,B两地.
(1)A,B间的距离为 km.
(2)计划修一条从C到铁路AB的最.短.公.路.l,并在l上建一个维修站D,使D到A,C的距离相等,求C,D间的距离.
14.如图,长方体的长BE=15 cm,宽AB=10 cm,高AD=20 cm,点M在CH上,且CM=5 cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
15.如图①,老旧电视机屏幕的长宽比为4∶3,但是多数电影图像的长宽比为2.4∶1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度).
①该屏幕的长= 寸,宽= 寸.
②已知“屏幕浪费比=”,求该电视机屏幕的浪费比.
(2)为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(长方形ABCD)恰好包含面积相等且长宽比分别为4∶3的屏幕(长方形EFGH)与2.4∶1的屏幕(长方形MNPQ).求这种屏幕长宽的比值(参考数据:≈2.2,结果精确到0.1).
16.如图,某小区有两个喷泉A,B,两个喷泉的距离AB的长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120 m,BM的长为150 m.求供水点M到喷泉A,B需要铺设的管道总长.
1
参考答案
1.A 2.B 3.D 4.A
5.解:由题意得,∠NOA=40°,∠NOB=50°,OA=60海里,OB=80海里,
∴∠AOB=90°,
∴AB==100(海里),
∴此时两船相距100海里.
6.B
7.A 点拨:∵BD⊥CE,∴∠BDC=90°.
在Rt△CDB中,由勾股定理得:CD===15(m),
设风筝沿CD方向下降9 m至点M,连接BM,如图,
则CM=9 m,∴DM=CD-CM=15-9=6(m),
∴BM===10(m),
∴BC-BM=17-10=7(m),即松松同学应该往回收线7 m.
故选A.
8.8,6,10
9.50
10.B 点拨:过点C作CO⊥DM于O,∴∠COD=90°,∴CO2+DO2=CD2.∵∠CDE=45°,∴∠DCO=45°=∠CDE,
∴CO=DO.∴2CO2=CD2=1.22,∴CO=(米).
易知AB=MN+CO+FG,
∴FG=3.2-1.7-=(米),故选B.
11.15
12.解:连接AC,作BF⊥AC于F,
∵∠BCD=120°,A,C,D三点共线,
∴∠ACB=180°-∠BCD=60°,
∴∠CBF=30°,
∴CF=BC=15 cm,
∴BF==15 cm.
∵∠ABC=75°,
∴∠ABF=∠ABC-∠CBF=45°,
∴∠BAC=45°=∠ABF,
∴AF=BF=15 cm,
∴AD=AF+CF+CD=(115+15)cm.
即点A到地面的距离为(115+15)cm.
13.解:(1)20
(2)如图,过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交l于点D,连接AD.
易知CE=1-(-17)=18 (km),AE=12 km.
设CD=x km,则AD=CD=x km.
由勾股定理得x2=(18-x)2+122,解得x=13.
故CD=13 km.
14.解:分三种情况比较最短距离:
如图①所示,连接AM,AM==5(cm);
如图②所示,连接AM,AM==25(cm);
如图③所示,连接AM,AM==5(cm).
∵5cm>5cm>25 cm,
∴需要爬行的最短距离是25 cm.
15.解:(1)①16;12
②设在该屏幕上播放长宽比为2.4∶1的视频时,视频的宽为a寸.
∴16∶a=2.4∶1,解得a=.
∴黑色带子的宽的和=12-=(寸).
∴屏幕浪费比==.
(2)由题意得=,=,∴PQ=BC,FG=EF.
∵S长方形EFGH=S长方形MNPQ,
∴BC·BC=EF·EF.
∴=,
∴=≈1.8.
答:这种屏幕长宽的比值约为1.8.
16.解:由题意得,AB=250 m,MN⊥AB,MN=120 m,BM=150 m.
在Rt△MNB中,BN===90(m),
∴AN=AB-BN=250-90=160(m),
在Rt△AMN中,AM===200(m),
∴供水点M到喷泉A,B需要铺设的管道总长=200+150=350(m).
