课题学习-镶嵌
图片预览







文档简介
课件22张PPT。7.4 课题学习镶嵌观察以下图案,说明它们都是由哪些几何图形组成?要设计地板图案,必须解决如下问题:1. 如果限于用一种正多边形镶嵌,哪几种多边形能镶嵌成一个平面?2. 如果允许用几种正多边形组合起来镶嵌,由哪几种多边形组合起来能镶嵌成一个平面?镶嵌:
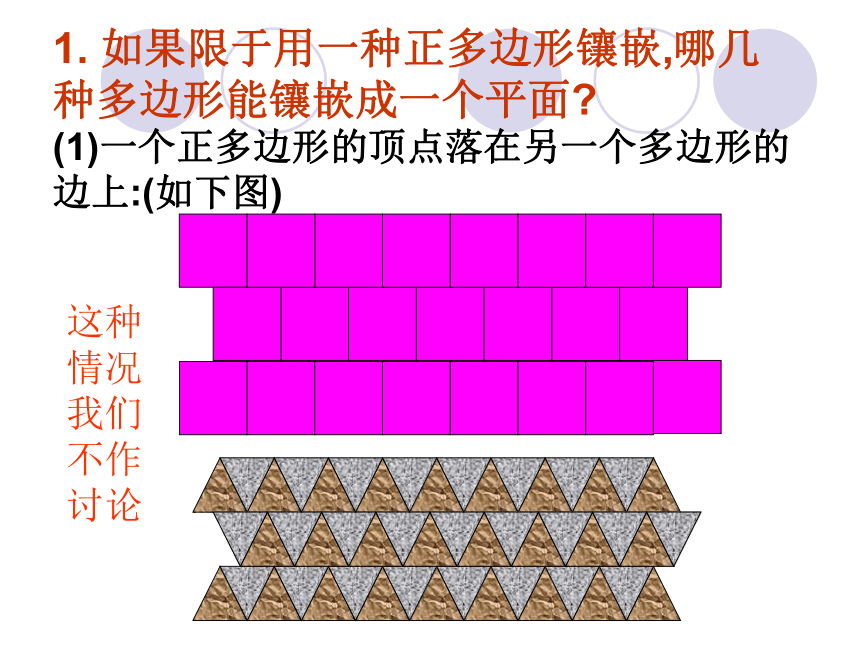
用形状、大小相同一种或几种平面图形,把地面或墙面既无缝隙、又不重叠地全部覆盖,在几何里叫做平面镶嵌。1. 如果限于用一种正多边形镶嵌,哪几种多边形能镶嵌成一个平面?(1)一个正多边形的顶点落在另一个多边形的边上:(如下图)这种情况我们不作讨论(2)一个正多边形的顶点不落在另一个多边形的边上:(如下图) 由图形可知:
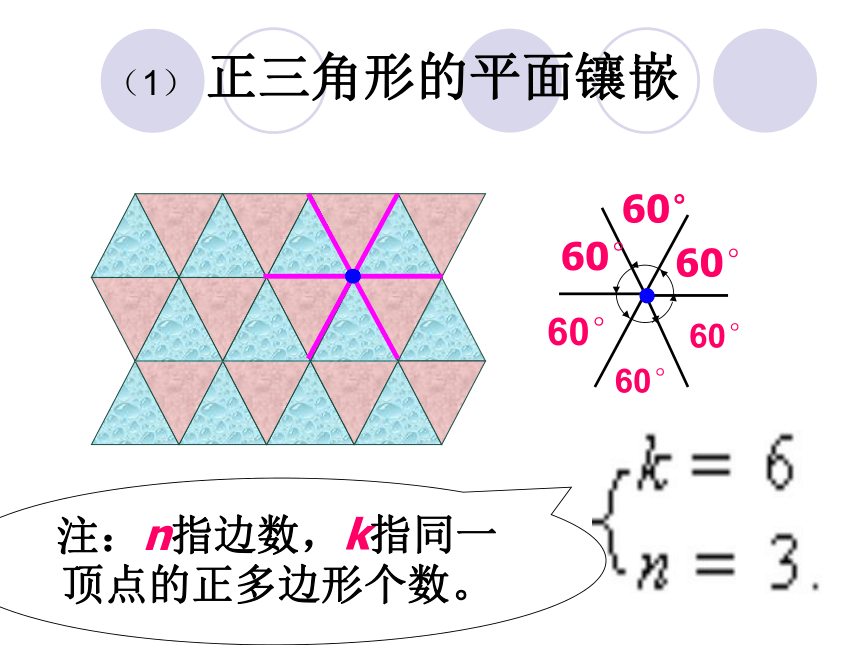
镶嵌的正多边形的边必须与另一个正多边形的边重合,于是,镶嵌的正多边形的边长都相等.还可以看到:镶嵌时,有几个正多边形的顶点相聚于一点.下面我们就研究这一类问题:问题:什么样的正多边形可以用来镶嵌呢?1.正三角形2. 正方形3.正五边形4.正六边形 由此,可以看到正三角形、正方形、正六边形可以作平面镶嵌,而正五边形不能作镶嵌,那么什么样的正多边形可以作镶嵌呢?(1) 正三角形的平面镶嵌60°60°60°60°60°60°注:n指边数,k指同一顶点的正多边形个数。(2) 正方形的平面镶嵌注:n、 k分别指同一顶点的正多边形边数、个数。(3) 正六边形的平面镶嵌注:n指边数,k指同一顶点的正多边形个数。因为正五边形的内角不能组成360°的角,而正三角形的内角能组成360°的角。而三角形的内角为180度,两个180度为360度,任意四边形的内角和为360度,所以三角形,四边形均可镶嵌成平面。由以上分析和讨论可知: 由一种正多边形进行镶嵌,只能有三种情况:( 1 )正三角形( 2 )正方形( 3 )正六边形 问题:由两种正多边形进行镶嵌,有几种情况呢?两种正多边形镶嵌
1、正三角形与正四边形能否进行镶嵌,若能,画出镶嵌的示意图,你能画出几个?
2、正三角形,正六边形能否进行镶嵌,若能有几种情况,画出镶嵌示意图。
3、正六边形能否与边数多于6的正多边形进行镶嵌?
4、怎样确定两种正多边形能否进行镶嵌,举例说明你的观点。1、若限用一种正多边形镶嵌,不可能是( )
A、正三角形 B、正方形 C、正五边形 D、正六边形
2、用两种正多边形镶嵌不能与正三角形匹配的正多边形是( )
A、正方形 B、正六边形 C、正十二边形 D、正十七边形练一练
3、明明家若想用边长相同的两种正多边形水泥砖铺地面,若其中一种为正六边形的水泥砖,请你帮助选择,你会再选择哪一种正多边形的水泥砖,试着画出 示意图。4,一种足球由黑白相间的牛皮缝制而成,黑皮是正五边形,白皮是正六边形,黑皮共12块,则白皮有( )块动手做一做1、搜集一些平面镶嵌图案,设计一、二个地板的平面镶嵌图
2、用硬纸任意剪出一些形状大小相同的三角形、四边形纸片,拼拼看,它们能否镶嵌成平面图案
(3)三种正多边形的平面镶嵌例图(1)正三角形与正方形图案注:m、 n分别指同一顶点处正三角形、正方形的个数。
返回120°120°60°60°(2)正三角形与正六边形的平面镶嵌图案(Ⅰ)(2)正三角形与正六边形的平面镶嵌图案(Ⅱ)60°60°120°60°60°每个顶点处正六边形1个,正三角形4个.返回
用形状、大小相同一种或几种平面图形,把地面或墙面既无缝隙、又不重叠地全部覆盖,在几何里叫做平面镶嵌。1. 如果限于用一种正多边形镶嵌,哪几种多边形能镶嵌成一个平面?(1)一个正多边形的顶点落在另一个多边形的边上:(如下图)这种情况我们不作讨论(2)一个正多边形的顶点不落在另一个多边形的边上:(如下图) 由图形可知:
镶嵌的正多边形的边必须与另一个正多边形的边重合,于是,镶嵌的正多边形的边长都相等.还可以看到:镶嵌时,有几个正多边形的顶点相聚于一点.下面我们就研究这一类问题:问题:什么样的正多边形可以用来镶嵌呢?1.正三角形2. 正方形3.正五边形4.正六边形 由此,可以看到正三角形、正方形、正六边形可以作平面镶嵌,而正五边形不能作镶嵌,那么什么样的正多边形可以作镶嵌呢?(1) 正三角形的平面镶嵌60°60°60°60°60°60°注:n指边数,k指同一顶点的正多边形个数。(2) 正方形的平面镶嵌注:n、 k分别指同一顶点的正多边形边数、个数。(3) 正六边形的平面镶嵌注:n指边数,k指同一顶点的正多边形个数。因为正五边形的内角不能组成360°的角,而正三角形的内角能组成360°的角。而三角形的内角为180度,两个180度为360度,任意四边形的内角和为360度,所以三角形,四边形均可镶嵌成平面。由以上分析和讨论可知: 由一种正多边形进行镶嵌,只能有三种情况:( 1 )正三角形( 2 )正方形( 3 )正六边形 问题:由两种正多边形进行镶嵌,有几种情况呢?两种正多边形镶嵌
1、正三角形与正四边形能否进行镶嵌,若能,画出镶嵌的示意图,你能画出几个?
2、正三角形,正六边形能否进行镶嵌,若能有几种情况,画出镶嵌示意图。
3、正六边形能否与边数多于6的正多边形进行镶嵌?
4、怎样确定两种正多边形能否进行镶嵌,举例说明你的观点。1、若限用一种正多边形镶嵌,不可能是( )
A、正三角形 B、正方形 C、正五边形 D、正六边形
2、用两种正多边形镶嵌不能与正三角形匹配的正多边形是( )
A、正方形 B、正六边形 C、正十二边形 D、正十七边形练一练
3、明明家若想用边长相同的两种正多边形水泥砖铺地面,若其中一种为正六边形的水泥砖,请你帮助选择,你会再选择哪一种正多边形的水泥砖,试着画出 示意图。4,一种足球由黑白相间的牛皮缝制而成,黑皮是正五边形,白皮是正六边形,黑皮共12块,则白皮有( )块动手做一做1、搜集一些平面镶嵌图案,设计一、二个地板的平面镶嵌图
2、用硬纸任意剪出一些形状大小相同的三角形、四边形纸片,拼拼看,它们能否镶嵌成平面图案
(3)三种正多边形的平面镶嵌例图(1)正三角形与正方形图案注:m、 n分别指同一顶点处正三角形、正方形的个数。
返回120°120°60°60°(2)正三角形与正六边形的平面镶嵌图案(Ⅰ)(2)正三角形与正六边形的平面镶嵌图案(Ⅱ)60°60°120°60°60°每个顶点处正六边形1个,正三角形4个.返回
