函数①(江苏省镇江市句容市)

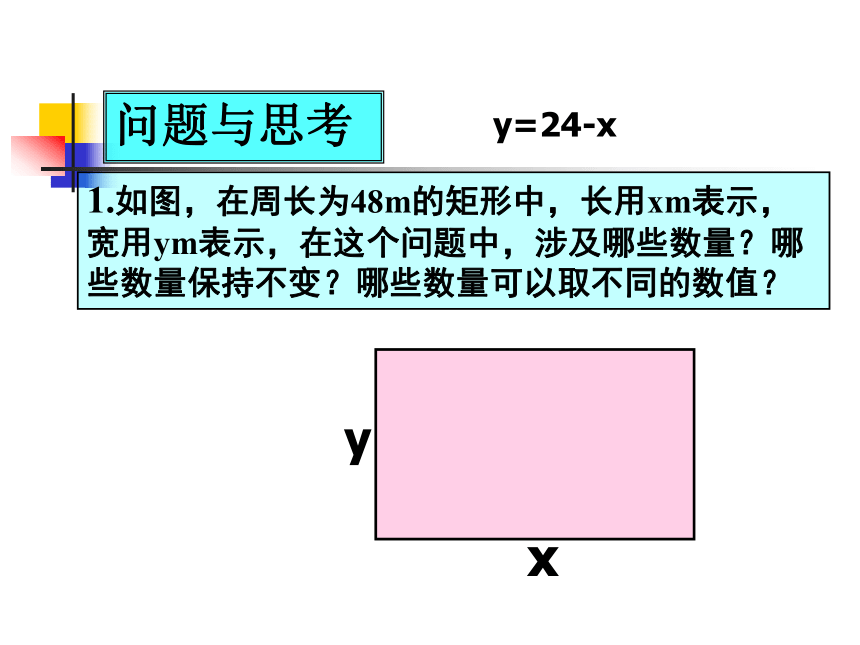
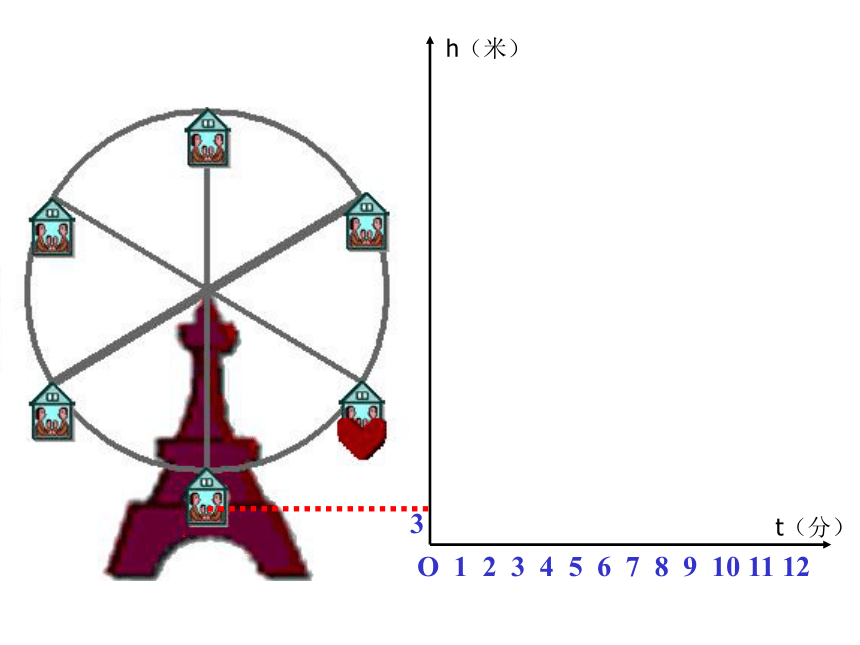
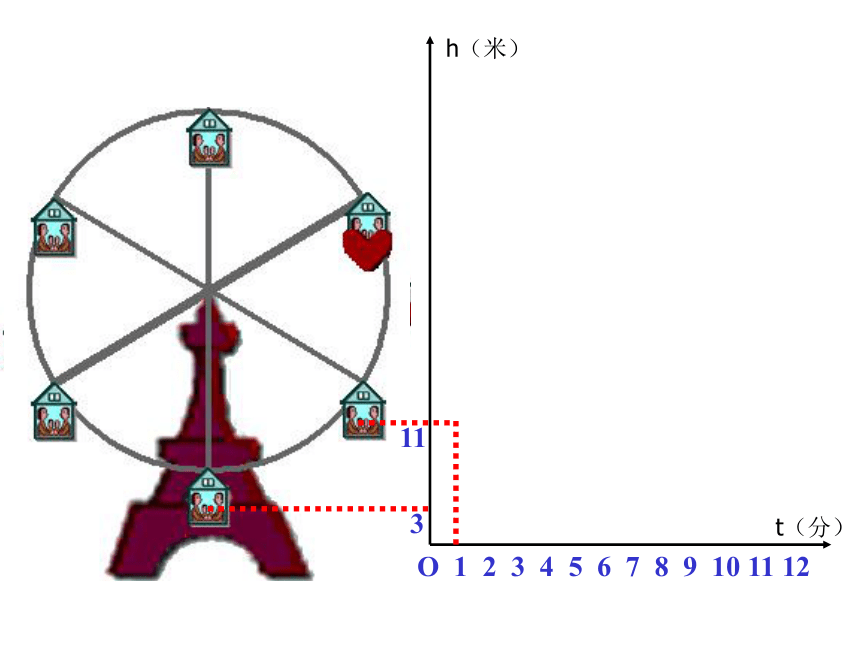
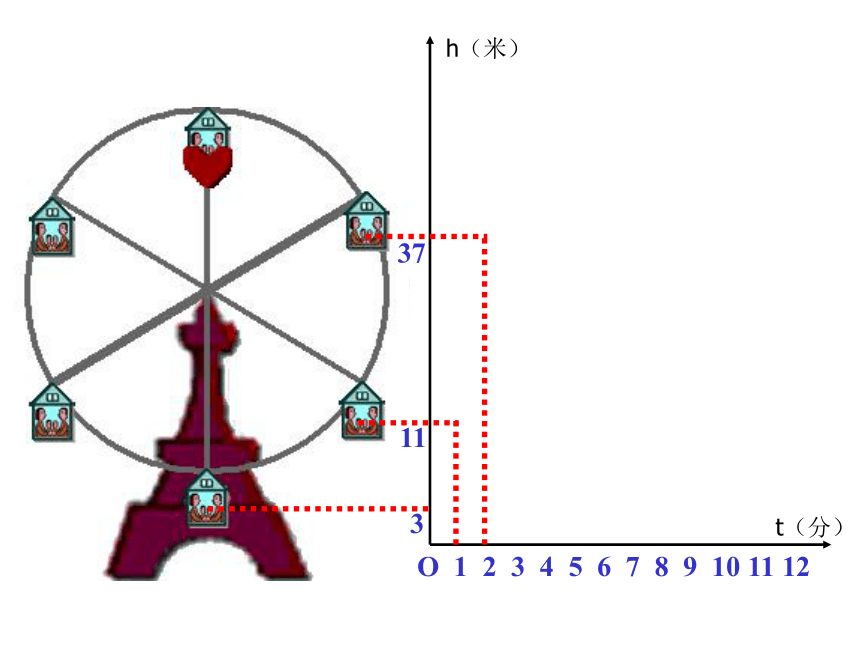
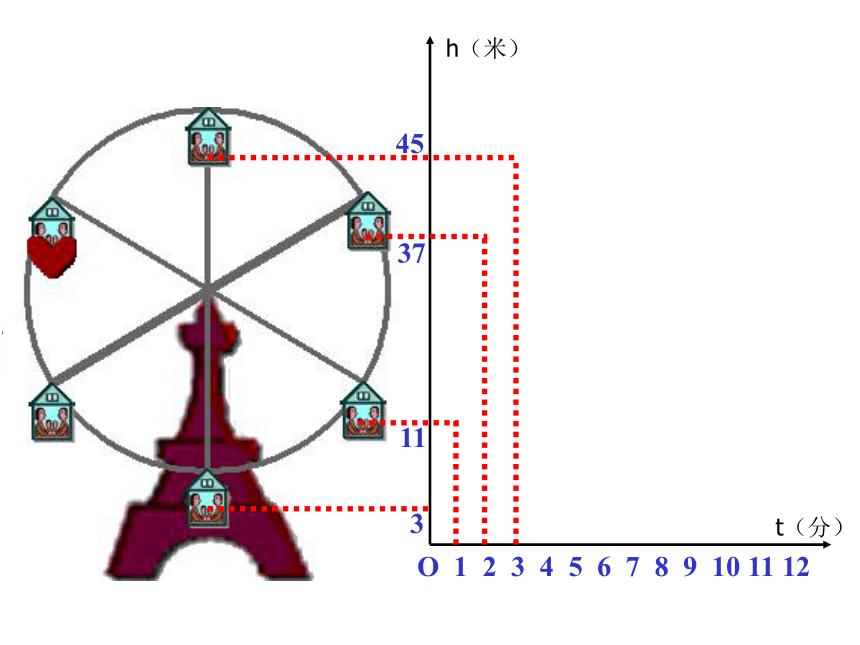
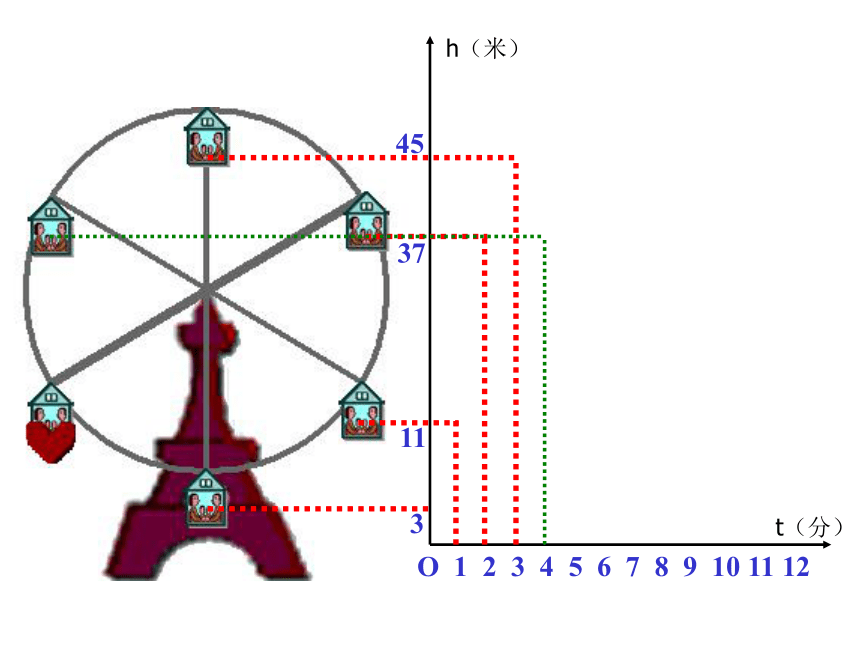
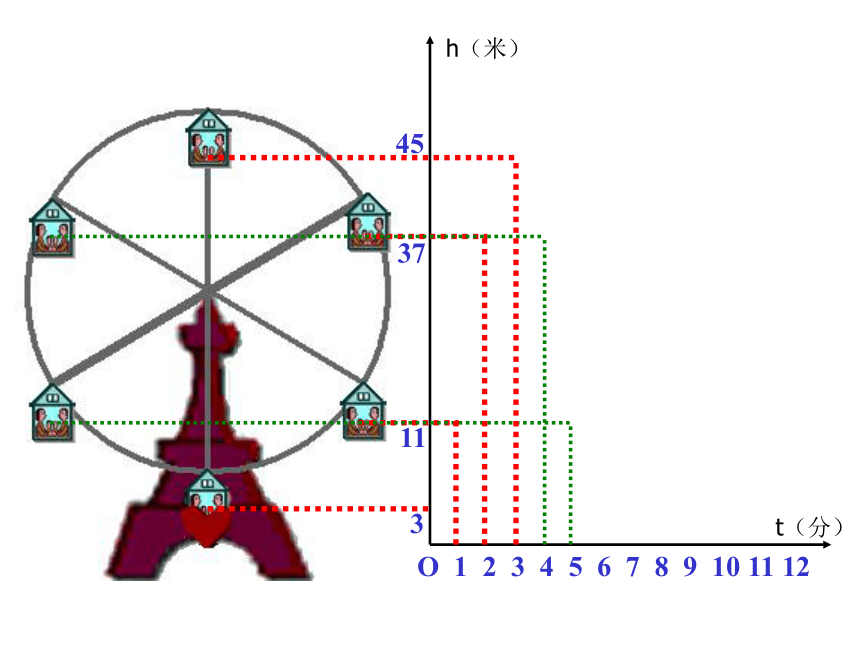
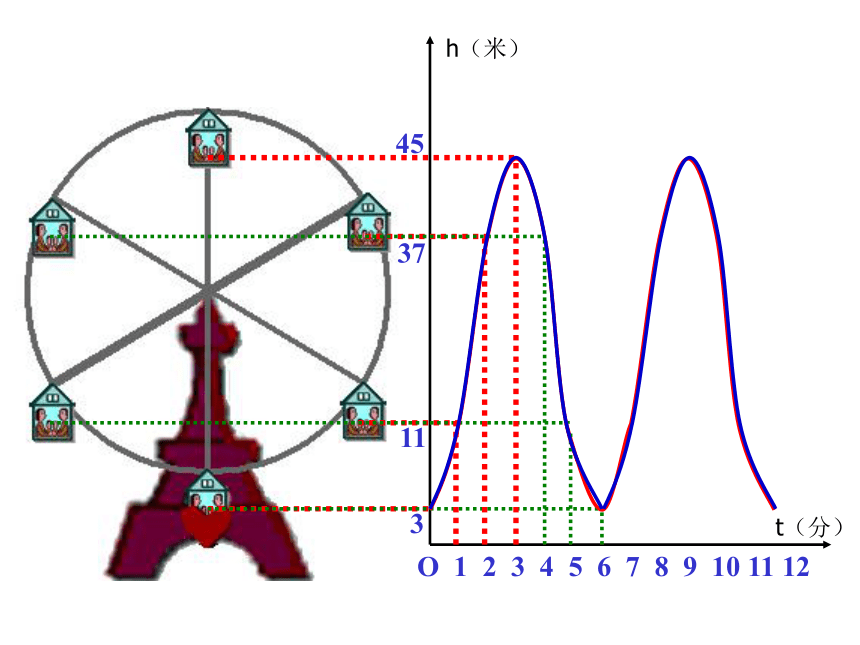
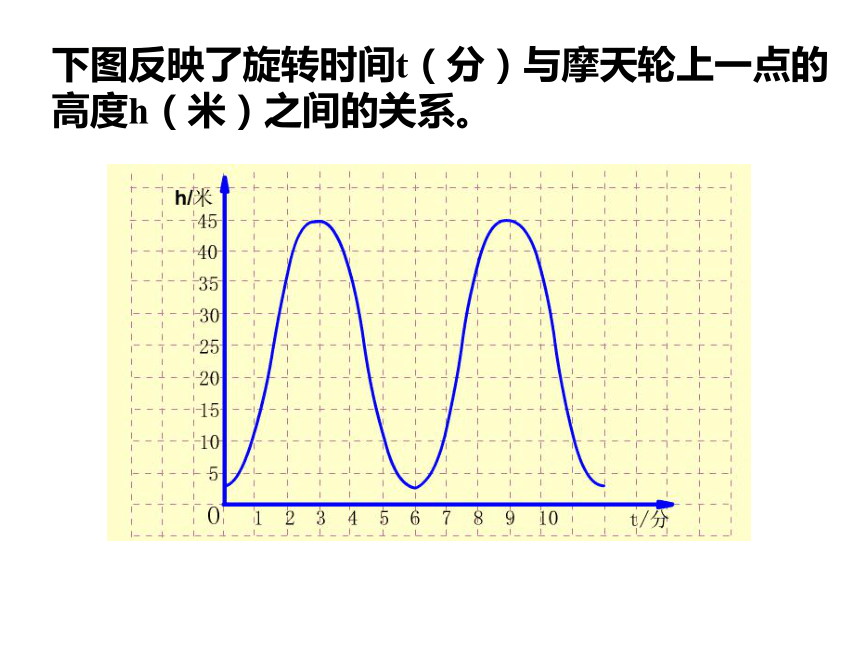
课件33张PPT。1.如图，在周长为48m的矩形中，长用xm表示，宽用ym表示，在这个问题中，涉及哪些数量？哪些数量保持不变？哪些数量可以取不同的数值？xy问题与思考y=24-x2.一列客车以240km/h的速度，从甲地驶往乙地，在这个问题中，涉及哪些数量？哪些数量保持不变？哪些数量可以取不同的数值？问题与思考 在某一变化过程中，数值保持不变的量叫做常量，可以取不同的数值的量叫做变量情境1摩天轮O 1 2 3 4 5 6 7 8 9 10 11 123h（米）t（分）O 1 2 3 4 5 6 7 8 9 10 11 12311h（米）t（分）O 1 2 3 4 5 6 7 8 9 10 11 1231137h（米）t（分）O 1 2 3 4 5 6 7 8 9 10 11 123113745h（米）t（分）O 1 2 3 4 5 6 7 8 9 10 11 123113745h（米）t（分）O 1 2 3 4 5 6 7 8 9 10 11 123113745h（米）t（分）O 1 2 3 4 5 6 7 8 9 10 11 123113745h（米）t（分）下图反映了旋转时间t（分）与摩天轮上一点的高度h（米）之间的关系。情境2（1）工作人员将水库的水位变化与水库蓄水量变化情况列成下表： 你能从工作人员制作的表格中获得哪些信息？
水位高低与水库容量有什么关系？情境3 搭1条小鱼需要 根火柴，862602 搭2条小鱼需要 根火柴， …… 搭10条小鱼需要 根火柴， 搭100条小鱼需要 根火柴，搭n条小鱼需要 根火柴.14 （3）水滴激起的波纹可以看作是一个不断向外扩展的圆，变化中圆的面积与半径的大小密切相关，你能大致描述他们之间的关系吗？情境4 在一个变化过程中，有两个变量。当其中一个变量变化时，另一个变量也随着发生变化。当一个变量确定时，另一个变量也随着确定。上述问题有共同之处吗？思考S=8+6(n-1)函数
一般的，如果在一个变化的过程中有两个变量x、y，并且对于变量x的每一个值，变量y都有惟一的值与它对应，那么我们称y是x的函数。其中x是自变量，y是因变量。
也可以说y和x之间存在着函数关系。概念①一个变化过程，
②两个变量x，y
③对于变量x的每一个值, 变量y都有惟一的值与它对应
我们称y是x的函数, 其中x是自变量, y是因变量.函数的概念思考S=8+6(n-1)高度h是时间t的函数你能说出变化过程中的函数关系吗？蓄水量是水位的函数火柴根数S是小鱼条数n的函数表示两个变量之间的式子称为函数关系式１．把一根1米长的铁丝围成一个长方形．（1）当长方形的宽为0.1m时，长为多少？（2）当长方形的宽为0.2m时，长为多少？（3）长方形的长是宽的函数吗？为什么？课堂练习２.按图示的运算程序，输入一个实数x，便可输出一个相应的实数y，y是x的函数吗？为什么？课堂练习y是x的函数吗?y是x的函数吗?y是x的函数吗? 3.指出下面题中的常量、自变量、与函数。并写出它们的函数关系式。
（1）圆周长C与半径R之间的关系；
（2）汽车从40km/h的速度正常行驶，行驶的路程S（km）与t（h）之间的关系。课堂练习33353739414304812162024283236404448温度/摄氏度时间/时 4. 如图，骆驼的体温随时间的变化而发生较大的变化。在这个问题中有变化的数量吗？哪些是自变量？哪些是因变量？课堂练习5.设等腰三角形的周长为60，腰长为x，底为y。
（1）写出y与x之间的函数关系式；
（2）求出当x＝20时，y的值，并求出此时三角形的面积。课堂练习6. 沙漏是我国计量时间的一种仪器，他根据一个容器里的细沙漏到另一个容器中的数量来计量时间。请说出这个变化过程中的自变量。课堂练习8.(1) 圆面积s与直径d之间的关系式为 ，其中变量是 ，常量是 ，自变量为 ，因变量为 ， 是 的函数.
(2) 一斤苹果1.2元，买x斤这样的苹果y元，其中变量是 ,常量是 ,自变量为 ，因变量为 ， 是 的函数.
(3) 写一个日常生活中遇到的函数关系的例子，并指出其中的常量与变量、自变量与因变量.课堂练习9. 指出下列变化过程中的常量与变量，自变量与函数： （1）购买单价是0.4元的铅笔，总金额y（元） 与铅笔数n（个）的关系；（2）设地面气温是20℃，如果每升高1km，气温下降6℃，气温t（ ℃ ）与高度h（km）的关系。课堂练习10.下列说法正确的个数为：
（1）矩形的宽一定，它的面积是长的函数
（2）人的体重y（公斤）是年龄x（岁）的函数
（3）x+3是自变量x的函数
（4）正方形的边长一定，它的面积是周长的函数
A. 1 B. 2 C. 3 D. 4课堂练习11.假设汽车在公路上以每小时80公里的速度匀速行驶，路程s（公里）是时间t（小时）的函数吗？你能写出这个函数关系式吗？在函数关系式中，t可以取不同的值，但可以取任意值吗？ 课堂练习这节课你有哪些收获？ 1、四个概念 （1）常量与变量
（2）自变量与函数。
2、两个注意：（1）判断常量与变量
（2）理解函数概念把握三点。①一个变化过程，
②两个变量，
③对于自变量的每一个值，因变量都有惟一的值与它对应。再 见句容第二中学欢迎您