2.1.1 同底数幂的乘法 课件(共28张PPT)
文档属性
| 名称 | 2.1.1 同底数幂的乘法 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
2.1 整式的乘法
2.1.1 同底数幂的乘法
1.理解同底数幂的乘法法则,能熟练运用该法则解决与之相关的一些数学问题.
2.经历探索同底数幂乘法运算法则的过程,培养学生观察、猜想、推理和归纳的能力.
3.通过同底数幂的乘法法则的探索过程使学生感受到由特殊到一般再到特殊的数学思想,通过合作学习激发学生的探索热情,感受到成功的喜悦.
【教学重点】
同底数幂的乘法法则的探索过程和理解应用.
【教学难点】
同底数幂的乘法法则的理解.
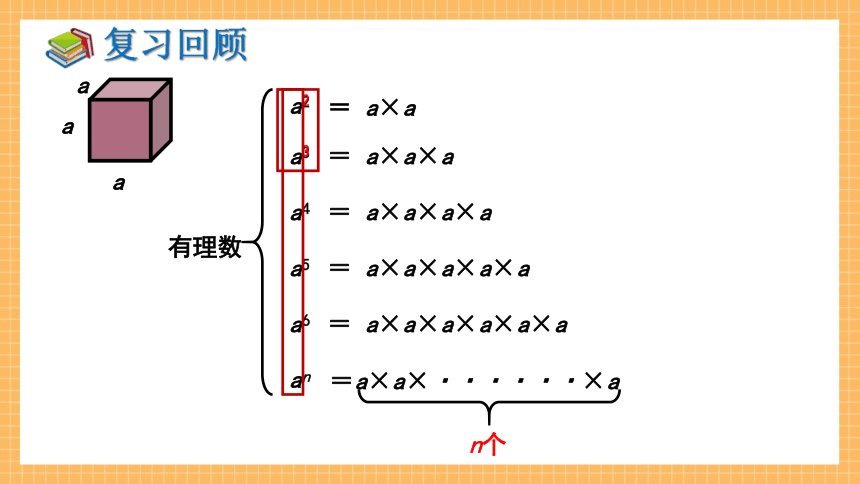
a
a
a2
a
a3
= a×a
= a×a×a
2
3
a4
a5
a6
an
= a×a×a×a
= a×a×a×a×a
= a×a×a×a×a×a
=a×a×······×a
n个
有理数
n
a
an
=a×a×······×a
n个
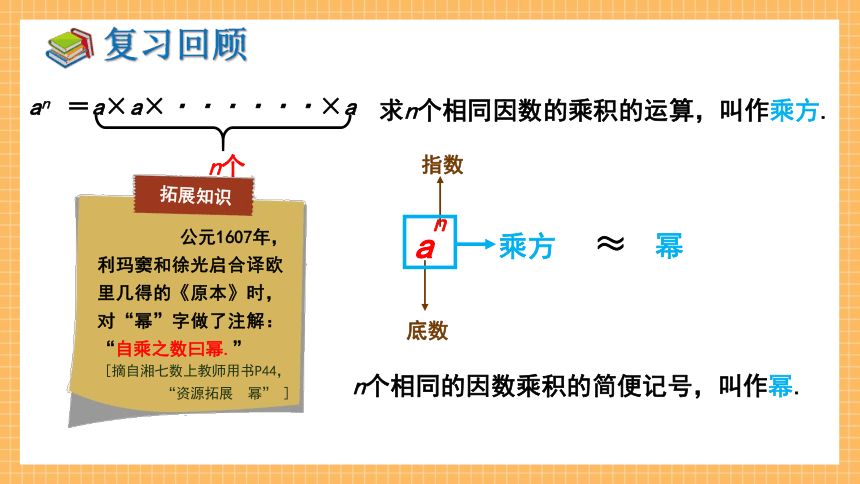
求n个相同因数的乘积的运算,叫作乘方.
底数
指数
乘方
幂
≈
n个相同的因数乘积的简便记号,叫作幂.
公元1607年,利玛窦和徐光启合译欧里几得的《原本》时,对“幂”字做了注解:“自乘之数曰幂.”
[摘自湘七数上教师用书P44, “资源拓展 幂” ]
拓展知识
思考
22×24= ; a2·a4= ;
a2·am= ;(m是正整数) am·an= .(m、n均为正整数)
22×24=(2×2)×(2×2×2×2)=2×2×2×2×2×2=26.
2个2
4个2
(2+4)个2
a2·a4=(a·a)·(a·a·a·a)=a·a·a·a·a·a=a6.
2个a
4个a
(2+4)个a
a2·am=(a·a)·(a·a·…·a·a)=a·a·…·a=a2+m.
2个a
m个a
(2+m)个a
通过观察,你发现上述式子的指数和底数是怎样变化的?
底数不变,指数相加.
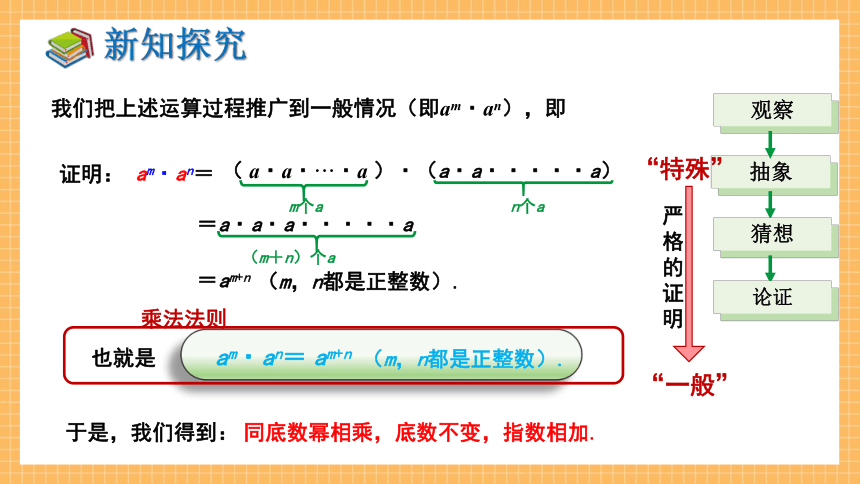
我们把上述运算过程推广到一般情况(即am·an),即
am·an =(a·a·…·a)·(a·a·…·a)
= a·a·…·a
= am+n(m,n都是正整数).
m个a
n个a
(m+n)个a
我们把上述运算过程推广到一般情况(即am·an),即
观察
抽象
猜想
论证
am·an= am+n
(m,n都是正整数).
也就是
am·an=
( a·a·····a )·(a·a·····a)
m个a
n个a
=a·a·a·····a
(m+n)个a
=am+n
(m,n都是正整数).
证明:
于是,我们得到:
同底数幂相乘,底数不变,指数相加.
“特殊”
“一般”
严格的证明
乘法法则
am · an = am+n (m,n 都是正整数).
同底数幂相乘,
底数 ,指数 .
不变
相加
同底数幂的乘法法则:
结果:①底数不变 ②指数相加
注意
条件:①乘法 ②底数相同
例 1
计算
(1)105×103;
(2)x3 · x4;
解: 105×103
= 105+3
= 108.
解:x3 · x4
= x3+4
= x7.
(1) -a·a3
解: -a·a3
= ﹣1·a1+3
=﹣a4
(2) y n · y n+1 (n为正整数)
解:yn · yn+1
= yn+n+1
= y2n+1.
例 2
计算
判断正误( 正确的打“ √ ”,错误的打“×”):
(1) x4 · x6 = x24 ( ) (2) x · x3 = x3 ( )
(3) x4 + x4 = x8 ( ) (4) x2 · x2 = 2x4 ( )
(5) (-x)2 · (-x)3 = (-x)5 ( )
(6) a2 · a3- a3 · a2 = 0 ( )
(7) x3 · y5 = (xy)8 ( )
(8) x7 + x7 = x14 ( )
√
√
×
×
×
×
×
×
对于计算出错的题目,你能分析出错的原因吗?试试看!
2、计算
(1) (2)
(3) (4)
1、公式·=( )中的底数,不仅可以是数、单项式,也可以是多项式等其他代数式;
2、同底数幂相乘时,如果有负号,要注意符号;
3、当底数互为相反数的幂相乘时,先统一底数,再计算。
类比同底数幂的乘法公式 am · an = am+n (m、n 都是正整数),
想一想:当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示 等于什么呢?
am · an · ap
当三个或三个以上的同底数幂相乘时,怎样用公式表示运算的结果呢?
am·an·ap =
( a·a··a )·(a·a··a) ·(a·a···a)
m个a
n个a
=a·a·a··a
(m+n+p)个a
=am+n+p
(m,n,p都是正整数).
证明:
am+n+p
如:
三个am·an·ap
(m,n,p都是正整数).
p个a
也就是
am·an·ap
=am+n+p
同理可知,若三个以上的同底数幂相乘,
底数______,
指数______.
不变
相加
【例3】计算:(1)32×33×34;
(2)y·y2·y4.
解法一:(1)32×33×34=(32×33)×34=35×34=39;
(2)y·y2·y4=(y·y2)·y4=y3·y4=y7.
解法二:(1)32×33×34=32+3+4=39;
(2)y·y2·y4=y1+2+4=y7.
1.判断题
(1)x5 · x5= 2x5 ( )
(2)y5 + y5 = y10 ( )
(3)m10 ·m15 = x25 ( )
(4)(y-3x)5 · (3x-y)6 =( y-3x)11 ( )
错
错
对
对
1. 下面的计算对不对?如果不对,应当怎样改正?
(1) b3 · b3 = 2b3
(2) b3 + b3 = b6
(3) a · a5 · a3 = a8
(4)(-x)4 · (-x)4 = (-x)16
×
×
×
×
b3 · b3 = b6
b3 + b3 = 2b3
a · a5 · a3 = a9
(-x)4 · (-x)4 = (-x)8
(1) x · x2 · x( ) = x7 ;
(2) xm ·( )= x3m ;
(3) 8 × 4 = 2x,则 x = ( ).
23×22 = 25
4
5
x2m
2. 填空:
3.计算:(1)2×23×25; (2)x2·x3·x4;
(3)-a5·a5; (4)am·a(m是正整数);
(5)xm+1·xm-1(其中m>1,且m是正整数).
答案:(1)29; (2)x9;
(3)-a10;(4)am+1.
(5)x2m.
A 组
(1) (-9)2×(-9)3
(2) (a-b)2·(a-b)3
(3) a4·(-a2)
4. 计算下列各题:
注意符号哟!
B 组
(1) xn + 1 · x2n
(2)
(3)
a · a2 + a3
= (-9)5.
= (a - b)5.
=-a6.
= x3n + 1.
= a3 + a3 = 2a3.
公式中的底数和指数可以是一个数、一个字母
或一个式子.
注意
5、光在真空中的速度约为 3×108 m/s,太阳光照射到地球上大约需要 5×102 s. 地球距离太阳大约有多远?
解:3×108×5×102
= 15×1010
= 1.5×1011 (m).
答:地球距离太阳大约有 1.5×1011 m.
6、已知,求的值。
(1)已知 an-3 · a2n+1 = a10 (a≠0,且 a≠±1),求 n 的值;
(2)已知 xa = 2,xb = 3,求 xa+b 的值.
公式逆用:am+n = am · an.
公式运用:am · an = am+n.
解:n-3 + 2n + 1 = 10,
n = 4.
解:xa+b = xa · xb = 2×3 = 6.
7、
同底数幂的乘法
幂的运算
am·an= am+n
(m,n都是正整数).
同底数幂相乘,底数不变,指数相加.
观察
抽象
猜想
论证
“数学思维”
“特殊”
“一般”
严格的证明
“归纳推理”过程
“特殊”
应用
1.布置作业:教材第30页“练习”.
2.完成同步练习册中本课时的练习.
2.1 整式的乘法
2.1.1 同底数幂的乘法
1.理解同底数幂的乘法法则,能熟练运用该法则解决与之相关的一些数学问题.
2.经历探索同底数幂乘法运算法则的过程,培养学生观察、猜想、推理和归纳的能力.
3.通过同底数幂的乘法法则的探索过程使学生感受到由特殊到一般再到特殊的数学思想,通过合作学习激发学生的探索热情,感受到成功的喜悦.
【教学重点】
同底数幂的乘法法则的探索过程和理解应用.
【教学难点】
同底数幂的乘法法则的理解.
a
a
a2
a
a3
= a×a
= a×a×a
2
3
a4
a5
a6
an
= a×a×a×a
= a×a×a×a×a
= a×a×a×a×a×a
=a×a×······×a
n个
有理数
n
a
an
=a×a×······×a
n个
求n个相同因数的乘积的运算,叫作乘方.
底数
指数
乘方
幂
≈
n个相同的因数乘积的简便记号,叫作幂.
公元1607年,利玛窦和徐光启合译欧里几得的《原本》时,对“幂”字做了注解:“自乘之数曰幂.”
[摘自湘七数上教师用书P44, “资源拓展 幂” ]
拓展知识
思考
22×24= ; a2·a4= ;
a2·am= ;(m是正整数) am·an= .(m、n均为正整数)
22×24=(2×2)×(2×2×2×2)=2×2×2×2×2×2=26.
2个2
4个2
(2+4)个2
a2·a4=(a·a)·(a·a·a·a)=a·a·a·a·a·a=a6.
2个a
4个a
(2+4)个a
a2·am=(a·a)·(a·a·…·a·a)=a·a·…·a=a2+m.
2个a
m个a
(2+m)个a
通过观察,你发现上述式子的指数和底数是怎样变化的?
底数不变,指数相加.
我们把上述运算过程推广到一般情况(即am·an),即
am·an =(a·a·…·a)·(a·a·…·a)
= a·a·…·a
= am+n(m,n都是正整数).
m个a
n个a
(m+n)个a
我们把上述运算过程推广到一般情况(即am·an),即
观察
抽象
猜想
论证
am·an= am+n
(m,n都是正整数).
也就是
am·an=
( a·a·····a )·(a·a·····a)
m个a
n个a
=a·a·a·····a
(m+n)个a
=am+n
(m,n都是正整数).
证明:
于是,我们得到:
同底数幂相乘,底数不变,指数相加.
“特殊”
“一般”
严格的证明
乘法法则
am · an = am+n (m,n 都是正整数).
同底数幂相乘,
底数 ,指数 .
不变
相加
同底数幂的乘法法则:
结果:①底数不变 ②指数相加
注意
条件:①乘法 ②底数相同
例 1
计算
(1)105×103;
(2)x3 · x4;
解: 105×103
= 105+3
= 108.
解:x3 · x4
= x3+4
= x7.
(1) -a·a3
解: -a·a3
= ﹣1·a1+3
=﹣a4
(2) y n · y n+1 (n为正整数)
解:yn · yn+1
= yn+n+1
= y2n+1.
例 2
计算
判断正误( 正确的打“ √ ”,错误的打“×”):
(1) x4 · x6 = x24 ( ) (2) x · x3 = x3 ( )
(3) x4 + x4 = x8 ( ) (4) x2 · x2 = 2x4 ( )
(5) (-x)2 · (-x)3 = (-x)5 ( )
(6) a2 · a3- a3 · a2 = 0 ( )
(7) x3 · y5 = (xy)8 ( )
(8) x7 + x7 = x14 ( )
√
√
×
×
×
×
×
×
对于计算出错的题目,你能分析出错的原因吗?试试看!
2、计算
(1) (2)
(3) (4)
1、公式·=( )中的底数,不仅可以是数、单项式,也可以是多项式等其他代数式;
2、同底数幂相乘时,如果有负号,要注意符号;
3、当底数互为相反数的幂相乘时,先统一底数,再计算。
类比同底数幂的乘法公式 am · an = am+n (m、n 都是正整数),
想一想:当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示 等于什么呢?
am · an · ap
当三个或三个以上的同底数幂相乘时,怎样用公式表示运算的结果呢?
am·an·ap =
( a·a··a )·(a·a··a) ·(a·a···a)
m个a
n个a
=a·a·a··a
(m+n+p)个a
=am+n+p
(m,n,p都是正整数).
证明:
am+n+p
如:
三个am·an·ap
(m,n,p都是正整数).
p个a
也就是
am·an·ap
=am+n+p
同理可知,若三个以上的同底数幂相乘,
底数______,
指数______.
不变
相加
【例3】计算:(1)32×33×34;
(2)y·y2·y4.
解法一:(1)32×33×34=(32×33)×34=35×34=39;
(2)y·y2·y4=(y·y2)·y4=y3·y4=y7.
解法二:(1)32×33×34=32+3+4=39;
(2)y·y2·y4=y1+2+4=y7.
1.判断题
(1)x5 · x5= 2x5 ( )
(2)y5 + y5 = y10 ( )
(3)m10 ·m15 = x25 ( )
(4)(y-3x)5 · (3x-y)6 =( y-3x)11 ( )
错
错
对
对
1. 下面的计算对不对?如果不对,应当怎样改正?
(1) b3 · b3 = 2b3
(2) b3 + b3 = b6
(3) a · a5 · a3 = a8
(4)(-x)4 · (-x)4 = (-x)16
×
×
×
×
b3 · b3 = b6
b3 + b3 = 2b3
a · a5 · a3 = a9
(-x)4 · (-x)4 = (-x)8
(1) x · x2 · x( ) = x7 ;
(2) xm ·( )= x3m ;
(3) 8 × 4 = 2x,则 x = ( ).
23×22 = 25
4
5
x2m
2. 填空:
3.计算:(1)2×23×25; (2)x2·x3·x4;
(3)-a5·a5; (4)am·a(m是正整数);
(5)xm+1·xm-1(其中m>1,且m是正整数).
答案:(1)29; (2)x9;
(3)-a10;(4)am+1.
(5)x2m.
A 组
(1) (-9)2×(-9)3
(2) (a-b)2·(a-b)3
(3) a4·(-a2)
4. 计算下列各题:
注意符号哟!
B 组
(1) xn + 1 · x2n
(2)
(3)
a · a2 + a3
= (-9)5.
= (a - b)5.
=-a6.
= x3n + 1.
= a3 + a3 = 2a3.
公式中的底数和指数可以是一个数、一个字母
或一个式子.
注意
5、光在真空中的速度约为 3×108 m/s,太阳光照射到地球上大约需要 5×102 s. 地球距离太阳大约有多远?
解:3×108×5×102
= 15×1010
= 1.5×1011 (m).
答:地球距离太阳大约有 1.5×1011 m.
6、已知,求的值。
(1)已知 an-3 · a2n+1 = a10 (a≠0,且 a≠±1),求 n 的值;
(2)已知 xa = 2,xb = 3,求 xa+b 的值.
公式逆用:am+n = am · an.
公式运用:am · an = am+n.
解:n-3 + 2n + 1 = 10,
n = 4.
解:xa+b = xa · xb = 2×3 = 6.
7、
同底数幂的乘法
幂的运算
am·an= am+n
(m,n都是正整数).
同底数幂相乘,底数不变,指数相加.
观察
抽象
猜想
论证
“数学思维”
“特殊”
“一般”
严格的证明
“归纳推理”过程
“特殊”
应用
1.布置作业:教材第30页“练习”.
2.完成同步练习册中本课时的练习.
