新人教版八年级上第十一章三角形全章导学案
文档属性
| 名称 | 新人教版八年级上第十一章三角形全章导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 227.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-03 19:38:52 | ||
图片预览

文档简介
11.1.1三角形的边导学案
一、学前准备
回忆你所学过或知道的三角形的有关知识。并写出来。
二、探索思考
知识点一:三角形概念及分类
1、学生自学课本2-3页探究之前内容,并完成下列问题:
(1)三角形概念:由不在同一直线上的三条线段___________________所组成的图形叫做三角形。
如图,线段____、______、______是三角形的边;点A、B、C是三角形的______; _____、 ______、_______是相邻两边组成的角,叫做三角形的内角,简称三角形的角。图中三角形记作__________。
△ABC的三边,也有时用a,b,c来表示。
(2)三边都相等的三角形叫做 三角形,如△DEF; 有两条边相等的三角形叫做 三角形,
如△ABC
如图1,等腰△ABC中,AB=AC,腰是__________,
底是_________,顶角是_______,底角是_____________.
等边三角形DEF是特殊的_______三角 ( http: / / www.21cnjy.com )形,DE=____=_____. 图1
(3)三角形按角分类可分为_____________、______________、_________________。
(4)三角形按边分类可分为 _____________
三角形 _____________
———————
_____________
练习一:
1、如图2.下列图形中是三角形的有______________
( http: / / www.21cnjy.com )
图2
2、图3中有几个三角形?用符号表示这些三角形.
知识点二:知道三角形三边的不等关系,并判断三条线段能否构成三角形
1、探究:请同学们画一个△ABC,分别量出AB,BC,AC的长,并比较下列各式的大小:
AB+BC_____AC AB+ AC _____ BC AC +BC _____ AB
从中你可以得出结论: ____ ____________ ,
将上面不等式移项可得出结论_____ _________________。
练习二:
1、下列长度的三条线段能否组成三角形?为什么?
(1)3,4,8; (2)5,6,11; (3)5,6,10
2、有四根木条,长度分别是12cm、10cm、8cm、4cm,选其中三根组成三角形,能组成三角形的个数是_______个。
3、如果三角形的两边长分别是3和5,那么第三边长可能是( )
A、1 B、9 C、3 D、10
三、当堂反馈
一个等腰三角形的两边长分别是2和5,则它的周长是( )
A、7 B、9 C、12 D、9或12
2、一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长。
11.1.2三角形的高,中线,角平分线导学案
一、学前准备
1、下列长度的三个线段能否组成三角形?
(1)3,6,8 (2)1,2,3 (3)6,8,2
二、探索思考
知识点一:认识并会画三角形的高线
自学课本第4页,并完成下列各题:
1、作出下列三角形三边上的高:
2、上面第1图中,AD是△ABC的边BC上的高,则∠ADC=∠ = °
3、由作图可得出如下结论:(1)三角形的三 ( http: / / www.21cnjy.com )条高线所在的直线相交于 点;(2)锐角三角形的三条高相交于三角形的 ;(3)钝角三角形的三条高所在直线相交于三角形的 ;(4)直角三角形的三条高相交三角形的 ;(5)交点我们叫做三角形的垂心。
练习一:如图所示,画△ABC的一边上的高,下列画法正确的是( ).
( http: / / www.21cnjy.com )
知识点二:认识并会画三角形的中线
自学课本4页三角形的中线并完成下列各题:
作出下列三角形三边上的中线
2、AD是△ABC的边BC上的中线,则有BD = = ,
3、由作图可得出如下结论: ( http: / / www.21cnjy.com )(1)三角形的三条中线相交于 点;(2)锐角三角形的三条中线相交于三角形的 ;(3)钝角三角形的三条中线相交于三角形的 ;(4)直角三角形的三条中线相交于三角形的 ;(5)交点我们叫做三角形的重心。
练习二:如图,D、E是边AC的三等分点 ( http: / / www.21cnjy.com ),图中有 个三角形,BD是⊿ 中 边上的中线,BE是⊿ 中________边上的中线;
知识点三:认识并会画三角形的角平分线
1、作出下列三角形三角的角平分线:
2、AD是△ABC中∠BAC的角平分线,则∠BAD=∠ =
3、由作图可得出如下结论:(1)三 ( http: / / www.21cnjy.com )角形的三条角平分线相交于 点;(2)锐角三角形的三条角平分线相交三角形的 ;(3)钝角三角形的三条角平分线相交三角形的 ;(4)直角三角形的三条角平分线相交三角形的 ;(5)交点我们叫做三角形的内心。
练习三:如图,已知∠1=∠BAC,∠2 =∠3,则∠BAC的平分线为 ,∠ABC的平分线为 .
总结:三角形的高、中线、角平分线都是一条线段。
三、当堂反馈
1.三角形的角平分线是( ).
A.直线 B.射线 C.线段 D.以上都不对
2.下列说法:①三角形的角平分线、 ( http: / / www.21cnjy.com )中线、高线都是线段;②直角三角形只有一条高线;③三角形的中线可能在三角形的外部;④三角形的高线都在三角形的内部,并且相交于一点,其中说法正确的有( ).
A.1个 B.2个 C.3个 D.4个
3.如图,AD是△ABC的高,AE是△ABC的角平分线,AF是△ABC的中线,
写出图中所有相等的角和相等的线段。
4.在△ABC中,AB=AC,AC边上的中线BD把三角形的周长分为12cm和15cm两部分,求三角形各边的长.
11.1.3三角形的稳定性导学案
知识点一:三角形的稳定性
自学课本6-7页内容,回答下列问题:
1、通过观察,你发现生活中哪些物体的结构是三角形?
二、做一做
1、用三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
2、用四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
3、在四边形的木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗?
4、如图4所示,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
5、想一想:在实际生活中还有哪些地方利用了“三角形的稳定性”来为我们服务?“四边形易变形”是优点还是缺点?生活中又有哪些应用?
练习
1. 如图,木工师傅做完门框后,为了防止变形 ( http: / / www.21cnjy.com ),常常像图中所示那样钉上两条斜拉的木条,这样做的数学道理是 ;
2.⑴ 下列图中哪些具有稳定性? 。
⑵ 对不具稳定性的图形,请适当地添加线段,使之具有稳定性。
3、造房子的屋顶常用三角结 ( http: / / www.21cnjy.com )构,从数学角度来看,是应用了______________,而活动接架则应用了四边形的_______________。
知识点二:通过练习进一步巩固三角形的边和相关线段
三、当堂反馈
1.如图:(1)在△ABC中,BC边上的高是________
(2)在△AEC中,AE边上的高是________
(3)在△FEC中,EC边上的高是_________
(4)若AB=CD=2cm,AE=3cm,则 =_______,CE=_______。
2.以下列各组线段长为边,能组成三角形的是 ( )
A.1cm,2cm,4cm; B.8cm,6cm,4cm C.12cm,5cm,6cm; D.2cm,3cm,6cm
3.已知等腰三角形的两边长分别为6cm和3cm,则该等腰三角形的周长是( )
A.9cm B. 12cm C. 12cm或15cm D. 15cm
4.如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
A.20米 B.15米 C.10米 D.5米
5、如图,点D是BC边上的中点,如果AB=3厘米,AC=4厘米,
则△ABD和△ACD的周长之差为________,面积之差为__________。
与三角形有关的线段练习
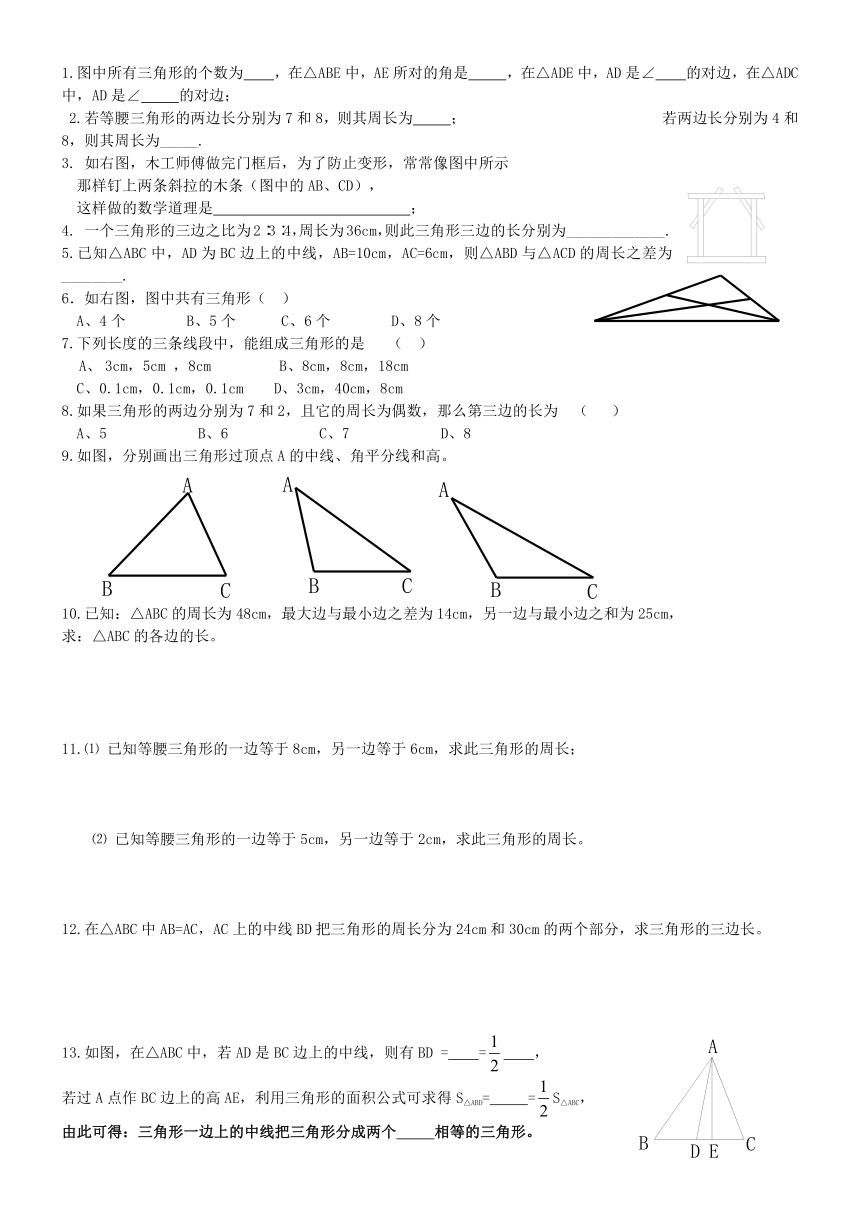
1.图中所有三角形的个数 ( http: / / www.21cnjy.com )为 ,在△ABE中,AE所对的角是 ,在△ADE中,AD是∠ 的对边,在△ADC中,AD是∠ 的对边;
2.若等腰三角形的两边长分别为7和8 ( http: / / www.21cnjy.com ),则其周长为 ; 若两边长分别为4和8,则其周长为_____.
3. 如右图,木工师傅做完门框后,为了防止变形,常常像图中所示
那样钉上两条斜拉的木条(图中的AB、CD),
这样做的数学道理是 ;
4. 一个三角形的三边之比为2∶3∶4,周长为36cm,则此三角形三边的长分别为_____________.
5.已知△ABC中,AD为BC边上的中线,AB=10cm,AC=6cm,则△ABD与△ACD的周长之差为________.
6.如右图,图中共有三角形( )
A、4个 B、5个 C、6个 D、8个
7.下列长度的三条线段中,能组成三角形的是 ( )
3cm,5cm ,8cm B、8cm,8cm,18cm
C、0.1cm,0.1cm,0.1cm D、3cm,40cm,8cm
8.如果三角形的两边分别为7和2,且它的周长为偶数,那么第三边的长为 ( )
A、5 B、6 C、7 D、8
9.如图,分别画出三角形过顶点A的中线、角平分线和高。
10.已知:△ABC的周长为48cm,最大边与最小边之差为14cm,另一边与最小边之和为25cm,
求:△ABC的各边的长。
11.⑴ 已知等腰三角形的一边等于8cm,另一边等于6cm,求此三角形的周长;
⑵ 已知等腰三角形的一边等于5cm,另一边等于2cm,求此三角形的周长。
12.在△ABC中AB=AC,AC上的中线BD把三角形的周长分为24cm和30cm的两个部分,求三角形的三边长。
13.如图,在△ABC中,若AD是BC边上的中线,则有BD = = ,
若过A点作BC边上的高AE,利用三角形的面积公式可求得S△ABD= =S△ABC,
由此可得:三角形一边上的中线把三角形分成两个 相等的三角形。
14.请你任意画一个三角形,将这个三角形的面积四等分。
11.2.1三角形的内角导学案
知识点一:探究三角形的内角和定理
1、自学课本11-13页内容,利用手中的硬纸片运用拼合法探究三角形的内角和。
由拼合过程你能想出证明三角形内角和等于180°的方法吗?
2、证明三角形的内角和定理
(1)阅读课本12页证明过程。
(2)仿照课本证明过程根据下面的辅助线做法,完成证明。
( http: / / www.21cnjy.com )
图一
归纳:三角形的内角和等于 。
知识点二:应用三角形内角和定理解决简单的实际问题
练习
1、填空:(1)在△ABC中,∠A = 60°∠B = 30°,则∠C = ;
(2)三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为 ;
(3)在△ABC中,∠A =∠B = 4∠C,则∠C = ;
(4)在△ABC中,∠A = 40°,∠B =∠C,则∠B = ;
2、例:如图,C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?
3、判断:
(1) 三角形中最大的角是,那么这个三角形是锐角三角形( )
(2) 一个三角形中最多只有一个钝角或直角( )
(3)一个等腰三角形一定是锐角三角形( )
(4) 一个三角形最少有一个角不大于( )
知识点三:直角三角形的两锐角关系
(一)、自主先学阅读课本P13回答下面的问题
1.三角形内角和是________,
2.若∠A=36°,则它的余角∠B=_______
3.如图11.2-5,在直角三角形ABC中,∠C=900,由三角形内角和定理,得
∠A+∠B+∠C= 即∠A+∠B+ = 1800
所以 ∠A+∠B =
4.直角三角形可以用符号 表示,直角三角形ABC可以写成 。
(二)、如图11.2-6,∠C=∠D=900,AD,BC相交于点E,∠CAE于∠DBC有什么关系?为什么?
如果一个三角形是直角三角形,那么这个三角形有两个角互余。反过来,有两个角互余的三角形是直角三角形吗?请你说说理由
巩固练习:
1.在△ABC中,∠ACB=90°CD⊥AB,那么与∠B互余的角有____________, 与∠B相等的角有___________
2.如图,AD⊥BC,∠1=∠2,∠C=650,求∠BAC的度数
11.2.2 三角形的外角导学案
一、学前准备
1.△ABC中,∠A=50°,∠B=60°,则∠C=________.
2.△ABC中,∠A:∠B:∠C=1:2:2,则∠A=_____,∠B=______,∠C=_______.
二、探索思考
知识一:三角形的外角概念
1、如图1,把△ABC的一边BC延长到D,得∠ACD,则∠ACD叫做三角形的
由此可以知道 组成的角叫三角形的外角。
2、找出右图中的外角 。
3、思考:
①在△ABC中,除了∠ACD外,还有那些外角?请在图2中分别画出来;
②以点C为顶点的外角有 个;所以,△ABC共有 个外角,
每一个顶点处的两个外角关系是 ;
③外角∠ACD与内角∠ACB的关系是:互为 角。
知识点二:三角形外角的两个性质
1、探究外角的性质
(1)如图9,△ABC中,∠A=70°,∠B=60°.∠ACD是△ABC的一个外角.能由∠A,∠B求出∠ACD吗?
如果能,∠ACD与∠A,∠B有什么关系?
(2)、任意一个三角形的一个外角与 ( http: / / www.21cnjy.com )它的内角有怎样的关系?能用一句话概述你的发现吗?
2、你能证明你发现的结论吗?
已知:如图4,∠ACD是△ABC的外角;
求证:
证明:
3.外角与其中一个不相邻的内角之间的大小关系呢?结论:_________________________________________
4.自学15页例4,从中你会发现什么结论?
练习
(1) 课本15页练习
(2)在△ABC中,∠B=50°,∠C的外角等于100°,则∠A=_____.
(3) 如右图所示,则∠a=________.
三、当堂反馈
1.若三角形的外角中有一个是锐角,则这个三角形是________三角形.
2.△ABC中,若∠C-∠B=∠A,则△ABC的外角中最小的角是______(填“锐角”、“直角”或“钝角”).
3.如图1,x=______.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3)
4.如图2,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系是_________.
5.如图3,在△ABC中,AE是角平分线,且∠B=52°,∠C=78°,求∠AEB的度数
6.如图所示,AE∥BD,∠1=95°,∠2=28°,求∠C
11.3.1 多边形导学案
探索思考
知识点一:多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念
1、自学课本79---80页,完成下列问题:
(1)在平面内,由一些线段________________相接组成的________叫做多边形。图1中分别是什么几边形?
(2)多边形_________组成的角叫做多边形的内角。图2中内角有____________________。
(3)多边形的边与它的的邻边的__________组成的角叫做
多边形的外角。图2中外角有______________________。
(4)连接多边形_________的两个顶点的线段叫做多边形的对角线。
(5)_________都相等,_________都相等的多边形叫做正多边形。
2、对应练习
(1)n边形有_______条边,______个顶点,________个内角。
(2)下列图形不是凸多边形的是( ).
知识点二:解决与多边形的对角线有关的问题
1、探究:画出下列多边形的对角线.回答问题:
(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了 个三角形;四边形共有____条对角线.
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了 个三角形;五边形共有____条对角线.
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了 个三角形;六边形共有____条对角线.
(4)猜想:
①从100边形的一个顶点出发可以画_____条对角线,把100边形分成了 个三角形;100边形共有___条对角线.
②从n边形的一个顶点出发可以画_____条对角线,把n分成了 个三角形;n边形共有_____条对角线.
练习:
(1)过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有2条对角线,则m-k=________.
(2)十二边形共有 条对角线,过一个顶点可作 条对角线,可把十二边形分成 个三角形。
三、当堂反馈
1、课本21页练习
2、下列图形中,是正多边形的是( )A.直角三角形 B.等腰三角形 C.长方形 D.正方形
3、九边形的对角线有( ) A.25条 B.31条 C.27条 D.30条
过n边形的一个顶点的所有对角线,把多边形分成8个三角形,则这个多边形的边数是_______。
一个多边形的对角线的条数等于它的边数的4倍,求这个多边形的边数 。
如图,是三角形ABC的不同三个外角,则
7、三角形的三个外角中最多有 锐角,最多有 个钝角,最多有 个直角
8、的两个内角的一平分线交于点E,,则
9、已知的的外角平分线交于点D,,那么= .
10、在中等于和它相邻的外角的四分之一,这个外角等于的两倍,那么
, ,
11.3.2多边形的内角和导学案
一、学前准备
1.三角形的内角和是 。
2.正方形、长方形的内角和是 。
3.从n边形的一个顶点出发可以画_____条对角线,把n边形分成了 个三角形;
二、探索思考
知识点一:多边形的内角和定理
探究1:任意画一个四边形,量出它的4个内角,计算它们的和。你能得出什么结论? 能否利用三角形内角和等于180°得出这个结论?
结论: 。
探究2:观察图3,请填空:
(1)从五边形的一个顶点出发,可以引_____条对角线,它们将五边形分为_____个三角形,五边形的内角和等于180°×______.
(2)从六边形的一个顶点出发,可以引_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于180°×______.
探究3:一般地, 从n边形的一个顶点出发 ( http: / / www.21cnjy.com ),可以引____条对角线,它们将n边形分为____个三角形,n边形的内角和等于180°×______.
结论:n多边形的内角和等于 。
练习一
1.十二边形的内角和是_________.
2.一个多边形的内角和等于900°,求它的边数.
知识点二:多边形的外角和
探究4:如图8,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
问题:如果将六边形换为n边形(n是大于等于3的整数),结果还相同吗?
因此可得结论: .
练习二
七边形的外角和是_________;十二边形的外角和是____________;三角形的外角和是_______。
一个多边形的每一个外角都等于36°则这个多边形是_______边形。
在每个内角都相等的多边形中,若一个外角是它相邻内角的,则这个多边形是______边形。
三、当堂反馈
1、一个多边形的每一个外角都等于40 ( http: / / www.21cnjy.com )°,则它的边数是__________;一个多边形的每一个内角都等于140°,则它的边数是___________。
2、如果四边形有一个角是直角,另外三个角的度数之比为2:3:4,那么这三个内角的度数分别为________。
3、若一个多边形的内角和为1080°,则它的边数是___________。
4、当一个多边形的边数增加1时,它的内角和增加_________度。
5、 正十边形的一个外角为______.
6、_______边形的内角和与外角和相等.
7、若一个多边形的内角和与外角和的比为7:2,求这个多边形的边数。
第十一章《三角形》诊断测试
一.选择题。(每题3分,共21分).
1.以下列各组线段为边,能组成三角形的是( )
A.2cm,3cm,5cm B.5cm,6cm,10cm
C.1cm,1cm,3cm D.3cm,4cm,9cm
2.等腰三角形的一边长等于4,一边长等于9,则它的周长是( )
A.17 B.22 C.17或22 D.13
3.一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是( )
A.5 B.6 C.7 D.8
4.直角三角形中两锐角平分线所交成的角的度数是( )
A.45° B.135° C.45°或135° D.都不对
5.一幅图案,在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个分别是正方形和正六边形,则第三个正多边形的边数是( )
A、3 B、5 C、8 D、12
6.已知∠1=48°,∠2的两边分别与∠1的两边垂直,则∠2=( )
A.48° B.132° C.42° D.48°或132°
7.已知等腰△ABC的底边BC=8cm,│AC-BC│=2cm,则腰AC的长为( )
A.10cm或6cm B.10cm C.6cm D.8cm或6cm
二.填空题。(每空3分,共27分)
8.三角形的三边长分别为5,1+2x,8,则x的取值范围是________.
9.四条线段的长分别为5cm、6cm、8cm、13cm,以其中任意三条线段为边可以构成________个三角形.
10.如图:∠A+∠B+∠C+∠D+∠E+∠F等于________.
11.如图,∠A=65°,∠B=75°,将纸片的一角折叠,若∠1=20°,则
∠2的度数为
12.n边形的每个外角都等于45°,则n=________.
13.等腰三角形一腰上的高与另一腰的夹角为20°,该等腰三角形的底角是
14. 如图,AB⊥BD于B,AC⊥CD于,且AC与BD交于点E。那么:
(1)△ADE的边DE上的高为 ,边AE上的高为 ;
(2)若AE=10,DE=2,CD=,则AB= 。
三.解答题。(共52分)
17、(8分)等腰三角形两边长为4cm、6cm,求等腰三角形的周长。
19、(8分)如图所示,有一块三角形A ( http: / / www.21cnjy.com )BC空地,要在这块空地上种植草皮来美化环境,已知这种草皮每平方米售价230元,AC=12m,BD=15m,购买这种草皮至少需要多少元?
20、(12分)一块三角形的试验田,需将该试验田划分为面积相等的四小块,种植四个不同的优良品种,设计四种不同划分方案,并给出说明。
21.(12分)如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,
求: (1) CD的长;
(2)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(3)作出△BCD的边BC边上的高DF,当BD=11cm 时,试求出DF的长。
28.(12分)(1)如图1, ( http: / / www.21cnjy.com )有一块含30°角的直角三角形XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=_______,∠XBC+∠XCB=_______.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2)
(2)如图2,改变直角三角板XYZ的位 ( http: / / www.21cnjy.com )置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
A
B
C
A
B
C
D
E
F
教师备课札记
教师备课札记
A
A
C
B
B
C
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
D
E
F
1
2
3
4
5
6
_
F
_
A
_
C
_
B
_
E
_
D
A
O
B
A
B
D
C
A
A
B
C
C
C
B
B
A
A
A
B
C
D
E
A
C
B
11.2-5
D
C
E
B
A
11.2-6
思考
A
C
B
D
教师备课札记
教师备课札记
教师备课札记
教师备课札记
一、学前准备
回忆你所学过或知道的三角形的有关知识。并写出来。
二、探索思考
知识点一:三角形概念及分类
1、学生自学课本2-3页探究之前内容,并完成下列问题:
(1)三角形概念:由不在同一直线上的三条线段___________________所组成的图形叫做三角形。
如图,线段____、______、______是三角形的边;点A、B、C是三角形的______; _____、 ______、_______是相邻两边组成的角,叫做三角形的内角,简称三角形的角。图中三角形记作__________。
△ABC的三边,也有时用a,b,c来表示。
(2)三边都相等的三角形叫做 三角形,如△DEF; 有两条边相等的三角形叫做 三角形,
如△ABC
如图1,等腰△ABC中,AB=AC,腰是__________,
底是_________,顶角是_______,底角是_____________.
等边三角形DEF是特殊的_______三角 ( http: / / www.21cnjy.com )形,DE=____=_____. 图1
(3)三角形按角分类可分为_____________、______________、_________________。
(4)三角形按边分类可分为 _____________
三角形 _____________
———————
_____________
练习一:
1、如图2.下列图形中是三角形的有______________
( http: / / www.21cnjy.com )
图2
2、图3中有几个三角形?用符号表示这些三角形.
知识点二:知道三角形三边的不等关系,并判断三条线段能否构成三角形
1、探究:请同学们画一个△ABC,分别量出AB,BC,AC的长,并比较下列各式的大小:
AB+BC_____AC AB+ AC _____ BC AC +BC _____ AB
从中你可以得出结论: ____ ____________ ,
将上面不等式移项可得出结论_____ _________________。
练习二:
1、下列长度的三条线段能否组成三角形?为什么?
(1)3,4,8; (2)5,6,11; (3)5,6,10
2、有四根木条,长度分别是12cm、10cm、8cm、4cm,选其中三根组成三角形,能组成三角形的个数是_______个。
3、如果三角形的两边长分别是3和5,那么第三边长可能是( )
A、1 B、9 C、3 D、10
三、当堂反馈
一个等腰三角形的两边长分别是2和5,则它的周长是( )
A、7 B、9 C、12 D、9或12
2、一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长。
11.1.2三角形的高,中线,角平分线导学案
一、学前准备
1、下列长度的三个线段能否组成三角形?
(1)3,6,8 (2)1,2,3 (3)6,8,2
二、探索思考
知识点一:认识并会画三角形的高线
自学课本第4页,并完成下列各题:
1、作出下列三角形三边上的高:
2、上面第1图中,AD是△ABC的边BC上的高,则∠ADC=∠ = °
3、由作图可得出如下结论:(1)三角形的三 ( http: / / www.21cnjy.com )条高线所在的直线相交于 点;(2)锐角三角形的三条高相交于三角形的 ;(3)钝角三角形的三条高所在直线相交于三角形的 ;(4)直角三角形的三条高相交三角形的 ;(5)交点我们叫做三角形的垂心。
练习一:如图所示,画△ABC的一边上的高,下列画法正确的是( ).
( http: / / www.21cnjy.com )
知识点二:认识并会画三角形的中线
自学课本4页三角形的中线并完成下列各题:
作出下列三角形三边上的中线
2、AD是△ABC的边BC上的中线,则有BD = = ,
3、由作图可得出如下结论: ( http: / / www.21cnjy.com )(1)三角形的三条中线相交于 点;(2)锐角三角形的三条中线相交于三角形的 ;(3)钝角三角形的三条中线相交于三角形的 ;(4)直角三角形的三条中线相交于三角形的 ;(5)交点我们叫做三角形的重心。
练习二:如图,D、E是边AC的三等分点 ( http: / / www.21cnjy.com ),图中有 个三角形,BD是⊿ 中 边上的中线,BE是⊿ 中________边上的中线;
知识点三:认识并会画三角形的角平分线
1、作出下列三角形三角的角平分线:
2、AD是△ABC中∠BAC的角平分线,则∠BAD=∠ =
3、由作图可得出如下结论:(1)三 ( http: / / www.21cnjy.com )角形的三条角平分线相交于 点;(2)锐角三角形的三条角平分线相交三角形的 ;(3)钝角三角形的三条角平分线相交三角形的 ;(4)直角三角形的三条角平分线相交三角形的 ;(5)交点我们叫做三角形的内心。
练习三:如图,已知∠1=∠BAC,∠2 =∠3,则∠BAC的平分线为 ,∠ABC的平分线为 .
总结:三角形的高、中线、角平分线都是一条线段。
三、当堂反馈
1.三角形的角平分线是( ).
A.直线 B.射线 C.线段 D.以上都不对
2.下列说法:①三角形的角平分线、 ( http: / / www.21cnjy.com )中线、高线都是线段;②直角三角形只有一条高线;③三角形的中线可能在三角形的外部;④三角形的高线都在三角形的内部,并且相交于一点,其中说法正确的有( ).
A.1个 B.2个 C.3个 D.4个
3.如图,AD是△ABC的高,AE是△ABC的角平分线,AF是△ABC的中线,
写出图中所有相等的角和相等的线段。
4.在△ABC中,AB=AC,AC边上的中线BD把三角形的周长分为12cm和15cm两部分,求三角形各边的长.
11.1.3三角形的稳定性导学案
知识点一:三角形的稳定性
自学课本6-7页内容,回答下列问题:
1、通过观察,你发现生活中哪些物体的结构是三角形?
二、做一做
1、用三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
2、用四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
3、在四边形的木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗?
4、如图4所示,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
5、想一想:在实际生活中还有哪些地方利用了“三角形的稳定性”来为我们服务?“四边形易变形”是优点还是缺点?生活中又有哪些应用?
练习
1. 如图,木工师傅做完门框后,为了防止变形 ( http: / / www.21cnjy.com ),常常像图中所示那样钉上两条斜拉的木条,这样做的数学道理是 ;
2.⑴ 下列图中哪些具有稳定性? 。
⑵ 对不具稳定性的图形,请适当地添加线段,使之具有稳定性。
3、造房子的屋顶常用三角结 ( http: / / www.21cnjy.com )构,从数学角度来看,是应用了______________,而活动接架则应用了四边形的_______________。
知识点二:通过练习进一步巩固三角形的边和相关线段
三、当堂反馈
1.如图:(1)在△ABC中,BC边上的高是________
(2)在△AEC中,AE边上的高是________
(3)在△FEC中,EC边上的高是_________
(4)若AB=CD=2cm,AE=3cm,则 =_______,CE=_______。
2.以下列各组线段长为边,能组成三角形的是 ( )
A.1cm,2cm,4cm; B.8cm,6cm,4cm C.12cm,5cm,6cm; D.2cm,3cm,6cm
3.已知等腰三角形的两边长分别为6cm和3cm,则该等腰三角形的周长是( )
A.9cm B. 12cm C. 12cm或15cm D. 15cm
4.如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
A.20米 B.15米 C.10米 D.5米
5、如图,点D是BC边上的中点,如果AB=3厘米,AC=4厘米,
则△ABD和△ACD的周长之差为________,面积之差为__________。
与三角形有关的线段练习
1.图中所有三角形的个数 ( http: / / www.21cnjy.com )为 ,在△ABE中,AE所对的角是 ,在△ADE中,AD是∠ 的对边,在△ADC中,AD是∠ 的对边;
2.若等腰三角形的两边长分别为7和8 ( http: / / www.21cnjy.com ),则其周长为 ; 若两边长分别为4和8,则其周长为_____.
3. 如右图,木工师傅做完门框后,为了防止变形,常常像图中所示
那样钉上两条斜拉的木条(图中的AB、CD),
这样做的数学道理是 ;
4. 一个三角形的三边之比为2∶3∶4,周长为36cm,则此三角形三边的长分别为_____________.
5.已知△ABC中,AD为BC边上的中线,AB=10cm,AC=6cm,则△ABD与△ACD的周长之差为________.
6.如右图,图中共有三角形( )
A、4个 B、5个 C、6个 D、8个
7.下列长度的三条线段中,能组成三角形的是 ( )
3cm,5cm ,8cm B、8cm,8cm,18cm
C、0.1cm,0.1cm,0.1cm D、3cm,40cm,8cm
8.如果三角形的两边分别为7和2,且它的周长为偶数,那么第三边的长为 ( )
A、5 B、6 C、7 D、8
9.如图,分别画出三角形过顶点A的中线、角平分线和高。
10.已知:△ABC的周长为48cm,最大边与最小边之差为14cm,另一边与最小边之和为25cm,
求:△ABC的各边的长。
11.⑴ 已知等腰三角形的一边等于8cm,另一边等于6cm,求此三角形的周长;
⑵ 已知等腰三角形的一边等于5cm,另一边等于2cm,求此三角形的周长。
12.在△ABC中AB=AC,AC上的中线BD把三角形的周长分为24cm和30cm的两个部分,求三角形的三边长。
13.如图,在△ABC中,若AD是BC边上的中线,则有BD = = ,
若过A点作BC边上的高AE,利用三角形的面积公式可求得S△ABD= =S△ABC,
由此可得:三角形一边上的中线把三角形分成两个 相等的三角形。
14.请你任意画一个三角形,将这个三角形的面积四等分。
11.2.1三角形的内角导学案
知识点一:探究三角形的内角和定理
1、自学课本11-13页内容,利用手中的硬纸片运用拼合法探究三角形的内角和。
由拼合过程你能想出证明三角形内角和等于180°的方法吗?
2、证明三角形的内角和定理
(1)阅读课本12页证明过程。
(2)仿照课本证明过程根据下面的辅助线做法,完成证明。
( http: / / www.21cnjy.com )
图一
归纳:三角形的内角和等于 。
知识点二:应用三角形内角和定理解决简单的实际问题
练习
1、填空:(1)在△ABC中,∠A = 60°∠B = 30°,则∠C = ;
(2)三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为 ;
(3)在△ABC中,∠A =∠B = 4∠C,则∠C = ;
(4)在△ABC中,∠A = 40°,∠B =∠C,则∠B = ;
2、例:如图,C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?
3、判断:
(1) 三角形中最大的角是,那么这个三角形是锐角三角形( )
(2) 一个三角形中最多只有一个钝角或直角( )
(3)一个等腰三角形一定是锐角三角形( )
(4) 一个三角形最少有一个角不大于( )
知识点三:直角三角形的两锐角关系
(一)、自主先学阅读课本P13回答下面的问题
1.三角形内角和是________,
2.若∠A=36°,则它的余角∠B=_______
3.如图11.2-5,在直角三角形ABC中,∠C=900,由三角形内角和定理,得
∠A+∠B+∠C= 即∠A+∠B+ = 1800
所以 ∠A+∠B =
4.直角三角形可以用符号 表示,直角三角形ABC可以写成 。
(二)、如图11.2-6,∠C=∠D=900,AD,BC相交于点E,∠CAE于∠DBC有什么关系?为什么?
如果一个三角形是直角三角形,那么这个三角形有两个角互余。反过来,有两个角互余的三角形是直角三角形吗?请你说说理由
巩固练习:
1.在△ABC中,∠ACB=90°CD⊥AB,那么与∠B互余的角有____________, 与∠B相等的角有___________
2.如图,AD⊥BC,∠1=∠2,∠C=650,求∠BAC的度数
11.2.2 三角形的外角导学案
一、学前准备
1.△ABC中,∠A=50°,∠B=60°,则∠C=________.
2.△ABC中,∠A:∠B:∠C=1:2:2,则∠A=_____,∠B=______,∠C=_______.
二、探索思考
知识一:三角形的外角概念
1、如图1,把△ABC的一边BC延长到D,得∠ACD,则∠ACD叫做三角形的
由此可以知道 组成的角叫三角形的外角。
2、找出右图中的外角 。
3、思考:
①在△ABC中,除了∠ACD外,还有那些外角?请在图2中分别画出来;
②以点C为顶点的外角有 个;所以,△ABC共有 个外角,
每一个顶点处的两个外角关系是 ;
③外角∠ACD与内角∠ACB的关系是:互为 角。
知识点二:三角形外角的两个性质
1、探究外角的性质
(1)如图9,△ABC中,∠A=70°,∠B=60°.∠ACD是△ABC的一个外角.能由∠A,∠B求出∠ACD吗?
如果能,∠ACD与∠A,∠B有什么关系?
(2)、任意一个三角形的一个外角与 ( http: / / www.21cnjy.com )它的内角有怎样的关系?能用一句话概述你的发现吗?
2、你能证明你发现的结论吗?
已知:如图4,∠ACD是△ABC的外角;
求证:
证明:
3.外角与其中一个不相邻的内角之间的大小关系呢?结论:_________________________________________
4.自学15页例4,从中你会发现什么结论?
练习
(1) 课本15页练习
(2)在△ABC中,∠B=50°,∠C的外角等于100°,则∠A=_____.
(3) 如右图所示,则∠a=________.
三、当堂反馈
1.若三角形的外角中有一个是锐角,则这个三角形是________三角形.
2.△ABC中,若∠C-∠B=∠A,则△ABC的外角中最小的角是______(填“锐角”、“直角”或“钝角”).
3.如图1,x=______.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3)
4.如图2,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系是_________.
5.如图3,在△ABC中,AE是角平分线,且∠B=52°,∠C=78°,求∠AEB的度数
6.如图所示,AE∥BD,∠1=95°,∠2=28°,求∠C
11.3.1 多边形导学案
探索思考
知识点一:多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念
1、自学课本79---80页,完成下列问题:
(1)在平面内,由一些线段________________相接组成的________叫做多边形。图1中分别是什么几边形?
(2)多边形_________组成的角叫做多边形的内角。图2中内角有____________________。
(3)多边形的边与它的的邻边的__________组成的角叫做
多边形的外角。图2中外角有______________________。
(4)连接多边形_________的两个顶点的线段叫做多边形的对角线。
(5)_________都相等,_________都相等的多边形叫做正多边形。
2、对应练习
(1)n边形有_______条边,______个顶点,________个内角。
(2)下列图形不是凸多边形的是( ).
知识点二:解决与多边形的对角线有关的问题
1、探究:画出下列多边形的对角线.回答问题:
(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了 个三角形;四边形共有____条对角线.
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了 个三角形;五边形共有____条对角线.
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了 个三角形;六边形共有____条对角线.
(4)猜想:
①从100边形的一个顶点出发可以画_____条对角线,把100边形分成了 个三角形;100边形共有___条对角线.
②从n边形的一个顶点出发可以画_____条对角线,把n分成了 个三角形;n边形共有_____条对角线.
练习:
(1)过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有2条对角线,则m-k=________.
(2)十二边形共有 条对角线,过一个顶点可作 条对角线,可把十二边形分成 个三角形。
三、当堂反馈
1、课本21页练习
2、下列图形中,是正多边形的是( )A.直角三角形 B.等腰三角形 C.长方形 D.正方形
3、九边形的对角线有( ) A.25条 B.31条 C.27条 D.30条
过n边形的一个顶点的所有对角线,把多边形分成8个三角形,则这个多边形的边数是_______。
一个多边形的对角线的条数等于它的边数的4倍,求这个多边形的边数 。
如图,是三角形ABC的不同三个外角,则
7、三角形的三个外角中最多有 锐角,最多有 个钝角,最多有 个直角
8、的两个内角的一平分线交于点E,,则
9、已知的的外角平分线交于点D,,那么= .
10、在中等于和它相邻的外角的四分之一,这个外角等于的两倍,那么
, ,
11.3.2多边形的内角和导学案
一、学前准备
1.三角形的内角和是 。
2.正方形、长方形的内角和是 。
3.从n边形的一个顶点出发可以画_____条对角线,把n边形分成了 个三角形;
二、探索思考
知识点一:多边形的内角和定理
探究1:任意画一个四边形,量出它的4个内角,计算它们的和。你能得出什么结论? 能否利用三角形内角和等于180°得出这个结论?
结论: 。
探究2:观察图3,请填空:
(1)从五边形的一个顶点出发,可以引_____条对角线,它们将五边形分为_____个三角形,五边形的内角和等于180°×______.
(2)从六边形的一个顶点出发,可以引_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于180°×______.
探究3:一般地, 从n边形的一个顶点出发 ( http: / / www.21cnjy.com ),可以引____条对角线,它们将n边形分为____个三角形,n边形的内角和等于180°×______.
结论:n多边形的内角和等于 。
练习一
1.十二边形的内角和是_________.
2.一个多边形的内角和等于900°,求它的边数.
知识点二:多边形的外角和
探究4:如图8,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
问题:如果将六边形换为n边形(n是大于等于3的整数),结果还相同吗?
因此可得结论: .
练习二
七边形的外角和是_________;十二边形的外角和是____________;三角形的外角和是_______。
一个多边形的每一个外角都等于36°则这个多边形是_______边形。
在每个内角都相等的多边形中,若一个外角是它相邻内角的,则这个多边形是______边形。
三、当堂反馈
1、一个多边形的每一个外角都等于40 ( http: / / www.21cnjy.com )°,则它的边数是__________;一个多边形的每一个内角都等于140°,则它的边数是___________。
2、如果四边形有一个角是直角,另外三个角的度数之比为2:3:4,那么这三个内角的度数分别为________。
3、若一个多边形的内角和为1080°,则它的边数是___________。
4、当一个多边形的边数增加1时,它的内角和增加_________度。
5、 正十边形的一个外角为______.
6、_______边形的内角和与外角和相等.
7、若一个多边形的内角和与外角和的比为7:2,求这个多边形的边数。
第十一章《三角形》诊断测试
一.选择题。(每题3分,共21分).
1.以下列各组线段为边,能组成三角形的是( )
A.2cm,3cm,5cm B.5cm,6cm,10cm
C.1cm,1cm,3cm D.3cm,4cm,9cm
2.等腰三角形的一边长等于4,一边长等于9,则它的周长是( )
A.17 B.22 C.17或22 D.13
3.一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是( )
A.5 B.6 C.7 D.8
4.直角三角形中两锐角平分线所交成的角的度数是( )
A.45° B.135° C.45°或135° D.都不对
5.一幅图案,在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个分别是正方形和正六边形,则第三个正多边形的边数是( )
A、3 B、5 C、8 D、12
6.已知∠1=48°,∠2的两边分别与∠1的两边垂直,则∠2=( )
A.48° B.132° C.42° D.48°或132°
7.已知等腰△ABC的底边BC=8cm,│AC-BC│=2cm,则腰AC的长为( )
A.10cm或6cm B.10cm C.6cm D.8cm或6cm
二.填空题。(每空3分,共27分)
8.三角形的三边长分别为5,1+2x,8,则x的取值范围是________.
9.四条线段的长分别为5cm、6cm、8cm、13cm,以其中任意三条线段为边可以构成________个三角形.
10.如图:∠A+∠B+∠C+∠D+∠E+∠F等于________.
11.如图,∠A=65°,∠B=75°,将纸片的一角折叠,若∠1=20°,则
∠2的度数为
12.n边形的每个外角都等于45°,则n=________.
13.等腰三角形一腰上的高与另一腰的夹角为20°,该等腰三角形的底角是
14. 如图,AB⊥BD于B,AC⊥CD于,且AC与BD交于点E。那么:
(1)△ADE的边DE上的高为 ,边AE上的高为 ;
(2)若AE=10,DE=2,CD=,则AB= 。
三.解答题。(共52分)
17、(8分)等腰三角形两边长为4cm、6cm,求等腰三角形的周长。
19、(8分)如图所示,有一块三角形A ( http: / / www.21cnjy.com )BC空地,要在这块空地上种植草皮来美化环境,已知这种草皮每平方米售价230元,AC=12m,BD=15m,购买这种草皮至少需要多少元?
20、(12分)一块三角形的试验田,需将该试验田划分为面积相等的四小块,种植四个不同的优良品种,设计四种不同划分方案,并给出说明。
21.(12分)如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,
求: (1) CD的长;
(2)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(3)作出△BCD的边BC边上的高DF,当BD=11cm 时,试求出DF的长。
28.(12分)(1)如图1, ( http: / / www.21cnjy.com )有一块含30°角的直角三角形XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=_______,∠XBC+∠XCB=_______.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2)
(2)如图2,改变直角三角板XYZ的位 ( http: / / www.21cnjy.com )置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
A
B
C
A
B
C
D
E
F
教师备课札记
教师备课札记
A
A
C
B
B
C
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
D
E
F
1
2
3
4
5
6
_
F
_
A
_
C
_
B
_
E
_
D
A
O
B
A
B
D
C
A
A
B
C
C
C
B
B
A
A
A
B
C
D
E
A
C
B
11.2-5
D
C
E
B
A
11.2-6
思考
A
C
B
D
教师备课札记
教师备课札记
教师备课札记
教师备课札记
