2021年广东省深圳中学自主招生数学试题(含答案)
文档属性
| 名称 | 2021年广东省深圳中学自主招生数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 127.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 15:34:52 | ||
图片预览

文档简介
2021年广东省深圳中学自主招生数学试题
一、数学填空题(1-10题,每题4分共40分)
1.(4分)计算:= .
2.(4分)计算:)2022= .
3.(4分)已知 xyz≠0,且x+2y+z=0,5x+4y﹣4z=0.设,其中m和n是两个互质的正整数,则10m+n= .
4.(4分)已知实数x,y满足,则17x2﹣10y2= .
5.(4分)如图,已知△ABC中,AB=10,D是AB的中点,∠DCA=90°,∠DCB=45°.则BC2= .
6.(4分)若反比例函数y=的图象与一次函数y=ax+b 的图象交于点 A(﹣2,m)=和B(7,n),则()4= .
7.(4分)定义新运算:=ad﹣bc,例如:=1×4﹣2×3=﹣2.已知实数x满足=,则x的最大值是 .
8.(4分)如图,已知直线RS,ST,TR都与⊙O相切,且,∠RST=90°,∠SRT=60°,RS=1,⊙O的直径为,其中a和b都是有理数,则100a+10b= .
9.(4分)在平面直角坐标系中,由抛物线y=6﹣x2与x轴所围出的区域内有 个整点(横纵坐标都是整数的点)(边界上的点不计).
10.(4分)满足(|x﹣2|﹣|x﹣6|)(|x﹣6|﹣|x﹣12|)(|x﹣12|﹣|x﹣21|)=0的全部实数x的乘积等于 .
二、数学填空题(11-15题,每题6分,共30分)
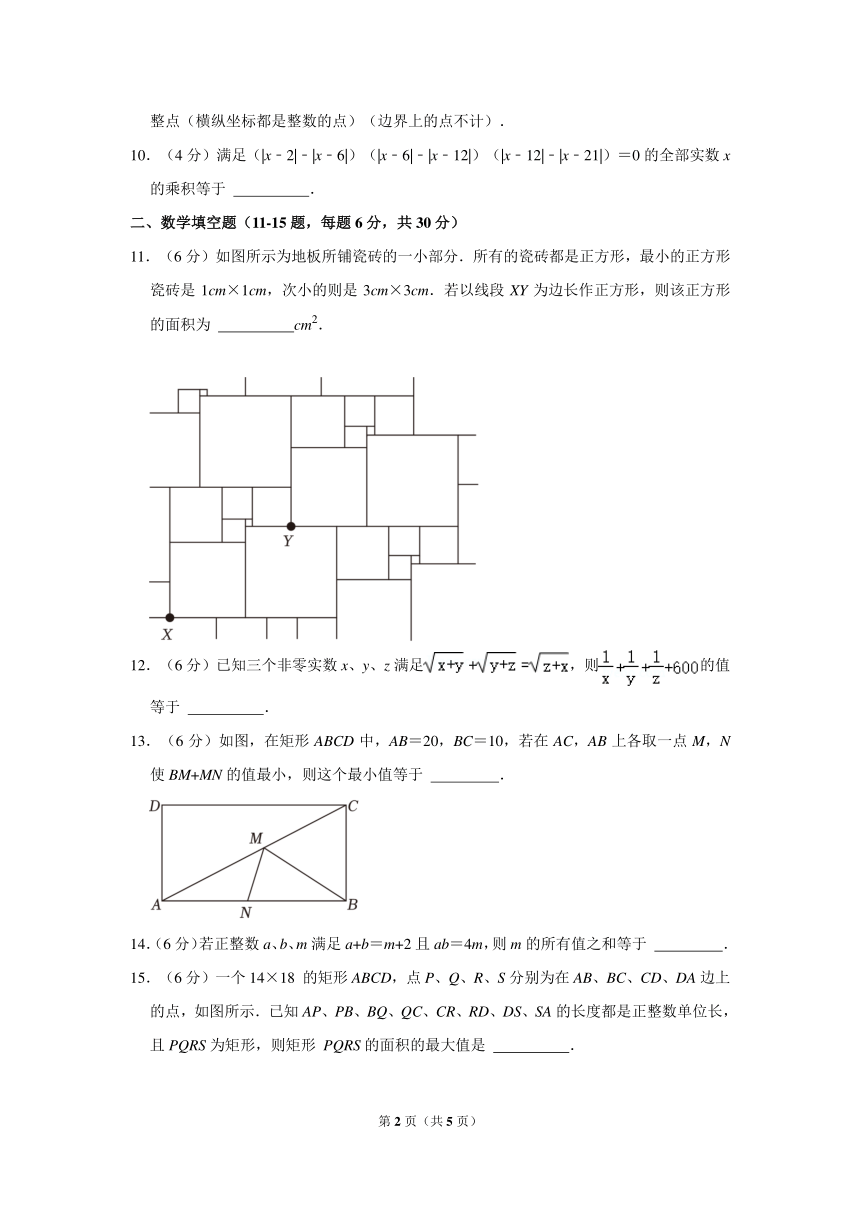
11.(6分)如图所示为地板所铺瓷砖的一小部分.所有的瓷砖都是正方形,最小的正方形瓷砖是1cm×1cm,次小的则是3cm×3cm.若以线段XY为边长作正方形,则该正方形的面积为 cm2.
12.(6分)已知三个非零实数x、y、z满足,则的值等于 .
13.(6分)如图,在矩形ABCD中,AB=20,BC=10,若在AC,AB上各取一点M,N使BM+MN的值最小,则这个最小值等于 .
14.(6分)若正整数a、b、m满足a+b=m+2且ab=4m,则m的所有值之和等于 .
15.(6分)一个14×18 的矩形ABCD,点P、Q、R、S分别为在AB、BC、CD、DA边上的点,如图所示.已知AP、PB、BQ、QC、CR、RD、DS、SA的长度都是正整数单位长,且PQRS为矩形,则矩形 PQRS的面积的最大值是 .
参考答案
一、数学填空题(1-10题,每题4分共40分)
1.308; 2.972; 3.196; 4.﹣22; 5.40; 6.625; 7.4; 8.330; 9.14; 10.594;
二、数学填空题(11-15题,每题6分,共30分)
11.解:如图:
∵图中的四边形均为正方形,且最小正方形的边长为1cm,次小正方形的边长为3cm,
∴CF=BF=3cm,则AB=4cm,HY=TH=5cm,
∴DF=AF=AB+BF=7cm,DE=BF-1=2cm,XD=CD=CF+DF=10cm,
∴EY=CD+HY+1=16cm,XE=XD+DE=12cm,
在Rt△EXY中,EY=16cm,XE=12cm,
由勾股定理得:XY2=EY2+XE2=162+122=400,
∴以线段XY为边长作正方形,则该正方形的面积为400cm2.;
12.600; 13.16;
解:∵a+b=m+2①,ab=4m ②,
①×4-②,得4a+4b-ab-8=0,
因式分解,得(a-4)(b-4)=8,
∵a,b均为正整数,
且8=1×8或8=2×4,
∴a-4=1,b-4=8 或a-4=2,b-4=4,
∴a=5,b=12 或a=6,b=8.
∴4m=5×12或4m=6×8,
∴m=15或m=12,
∴m的所有值之和等于27.
故答案为:27.;
15.解:根据题意:设AP=RC=a,AS=CQ=b,PB=DR=18-a,SD=BQ=14-b,
由△APS∽△DSR,则 a(18-a)=b(14-b),
又因为a,b是正整数,故a(18-a)=13,24,33,40,45,48,49,得a=3,15,则b=5或9,
即有(a,b)=(3,5),(15,5),(3,9),(15,9),
S=14×18-ab-(18-a)(14-b),
S=102,150,150,102,
即:Smax=150.
故答案为:150.
第1页(共1页)
一、数学填空题(1-10题,每题4分共40分)
1.(4分)计算:= .
2.(4分)计算:)2022= .
3.(4分)已知 xyz≠0,且x+2y+z=0,5x+4y﹣4z=0.设,其中m和n是两个互质的正整数,则10m+n= .
4.(4分)已知实数x,y满足,则17x2﹣10y2= .
5.(4分)如图,已知△ABC中,AB=10,D是AB的中点,∠DCA=90°,∠DCB=45°.则BC2= .
6.(4分)若反比例函数y=的图象与一次函数y=ax+b 的图象交于点 A(﹣2,m)=和B(7,n),则()4= .
7.(4分)定义新运算:=ad﹣bc,例如:=1×4﹣2×3=﹣2.已知实数x满足=,则x的最大值是 .
8.(4分)如图,已知直线RS,ST,TR都与⊙O相切,且,∠RST=90°,∠SRT=60°,RS=1,⊙O的直径为,其中a和b都是有理数,则100a+10b= .
9.(4分)在平面直角坐标系中,由抛物线y=6﹣x2与x轴所围出的区域内有 个整点(横纵坐标都是整数的点)(边界上的点不计).
10.(4分)满足(|x﹣2|﹣|x﹣6|)(|x﹣6|﹣|x﹣12|)(|x﹣12|﹣|x﹣21|)=0的全部实数x的乘积等于 .
二、数学填空题(11-15题,每题6分,共30分)
11.(6分)如图所示为地板所铺瓷砖的一小部分.所有的瓷砖都是正方形,最小的正方形瓷砖是1cm×1cm,次小的则是3cm×3cm.若以线段XY为边长作正方形,则该正方形的面积为 cm2.
12.(6分)已知三个非零实数x、y、z满足,则的值等于 .
13.(6分)如图,在矩形ABCD中,AB=20,BC=10,若在AC,AB上各取一点M,N使BM+MN的值最小,则这个最小值等于 .
14.(6分)若正整数a、b、m满足a+b=m+2且ab=4m,则m的所有值之和等于 .
15.(6分)一个14×18 的矩形ABCD,点P、Q、R、S分别为在AB、BC、CD、DA边上的点,如图所示.已知AP、PB、BQ、QC、CR、RD、DS、SA的长度都是正整数单位长,且PQRS为矩形,则矩形 PQRS的面积的最大值是 .
参考答案
一、数学填空题(1-10题,每题4分共40分)
1.308; 2.972; 3.196; 4.﹣22; 5.40; 6.625; 7.4; 8.330; 9.14; 10.594;
二、数学填空题(11-15题,每题6分,共30分)
11.解:如图:
∵图中的四边形均为正方形,且最小正方形的边长为1cm,次小正方形的边长为3cm,
∴CF=BF=3cm,则AB=4cm,HY=TH=5cm,
∴DF=AF=AB+BF=7cm,DE=BF-1=2cm,XD=CD=CF+DF=10cm,
∴EY=CD+HY+1=16cm,XE=XD+DE=12cm,
在Rt△EXY中,EY=16cm,XE=12cm,
由勾股定理得:XY2=EY2+XE2=162+122=400,
∴以线段XY为边长作正方形,则该正方形的面积为400cm2.;
12.600; 13.16;
解:∵a+b=m+2①,ab=4m ②,
①×4-②,得4a+4b-ab-8=0,
因式分解,得(a-4)(b-4)=8,
∵a,b均为正整数,
且8=1×8或8=2×4,
∴a-4=1,b-4=8 或a-4=2,b-4=4,
∴a=5,b=12 或a=6,b=8.
∴4m=5×12或4m=6×8,
∴m=15或m=12,
∴m的所有值之和等于27.
故答案为:27.;
15.解:根据题意:设AP=RC=a,AS=CQ=b,PB=DR=18-a,SD=BQ=14-b,
由△APS∽△DSR,则 a(18-a)=b(14-b),
又因为a,b是正整数,故a(18-a)=13,24,33,40,45,48,49,得a=3,15,则b=5或9,
即有(a,b)=(3,5),(15,5),(3,9),(15,9),
S=14×18-ab-(18-a)(14-b),
S=102,150,150,102,
即:Smax=150.
故答案为:150.
第1页(共1页)
同课章节目录
