2024年九年级中考数学解题技巧(3)方格纸上直尺画图(含答案)
文档属性
| 名称 | 2024年九年级中考数学解题技巧(3)方格纸上直尺画图(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 19:11:19 | ||
图片预览


文档简介
中考数学解题技巧(三)方格纸上直尺画图
一、考点:
(1)轴对称的性质
(2)平行线分线段的性质
(3)垂直平分线的性质
(4)特殊三角形、四边形的性质
(5)三角形全等、相似的性质
(6)三角函数、勾股定理
二、考查:
( 1 ) 画线段的中点(或等分点)、画对称点
(2) 画45角,找点
(3) 画平行线、垂线(或线段的垂直平分线),找点
(4) 画三角形全等、画三角形相似,找点
(5) 画轴对称图形,找点
三、举例:
例1、在平面直角坐标系中,点A(0,1),B(5,1),C(8,5),D(3,5),E(2,1),仅用无刻度的直尺在给定的网格中完成画图,画图过程用虚线表示,并回答下列问题.
(1)四边形ABCD的形状为 ;
(2)在AD上找点F,使AF=AE;
(3)分别在CD上找点M,BC上找点N,使四边形EFMN为矩形;
(4)将△ACF沿某条直线翻折后,点A,C,F的对应点均落在四边形ABCD的边上,请直接写出该直线的解析式为 .
【解答】(1)∵AB=CD=5,AD==5,BC==5,
∴AD=DC=CB=AB=5,
∴四边形ABCD是菱形.
故答案为:菱形.
(2)如图,点F即为所求.(菱形ABCD是轴对称图形,这里充分运用轴对称的性质画图。点B-D对应, 点E-F对应,线段BE,DF的交点在对称轴上,线段DE,BF的交点也在对称轴上。先连DE与对称轴的交点J,也是BF与对称轴的交点,这样连BJ就能找到点F。)
(3)如图,四边形EFMN即为所求.(图中MP平行于DB即可找到点N.)
(4)△ACF沿菱形ABCD的对角线翻折后,点A,C,F的对应点均落在四边形ABCD的边上,
对角线的解析式为y=﹣2x+11或y=x+1.
故答案为:y=﹣2x+11或y=x+1.
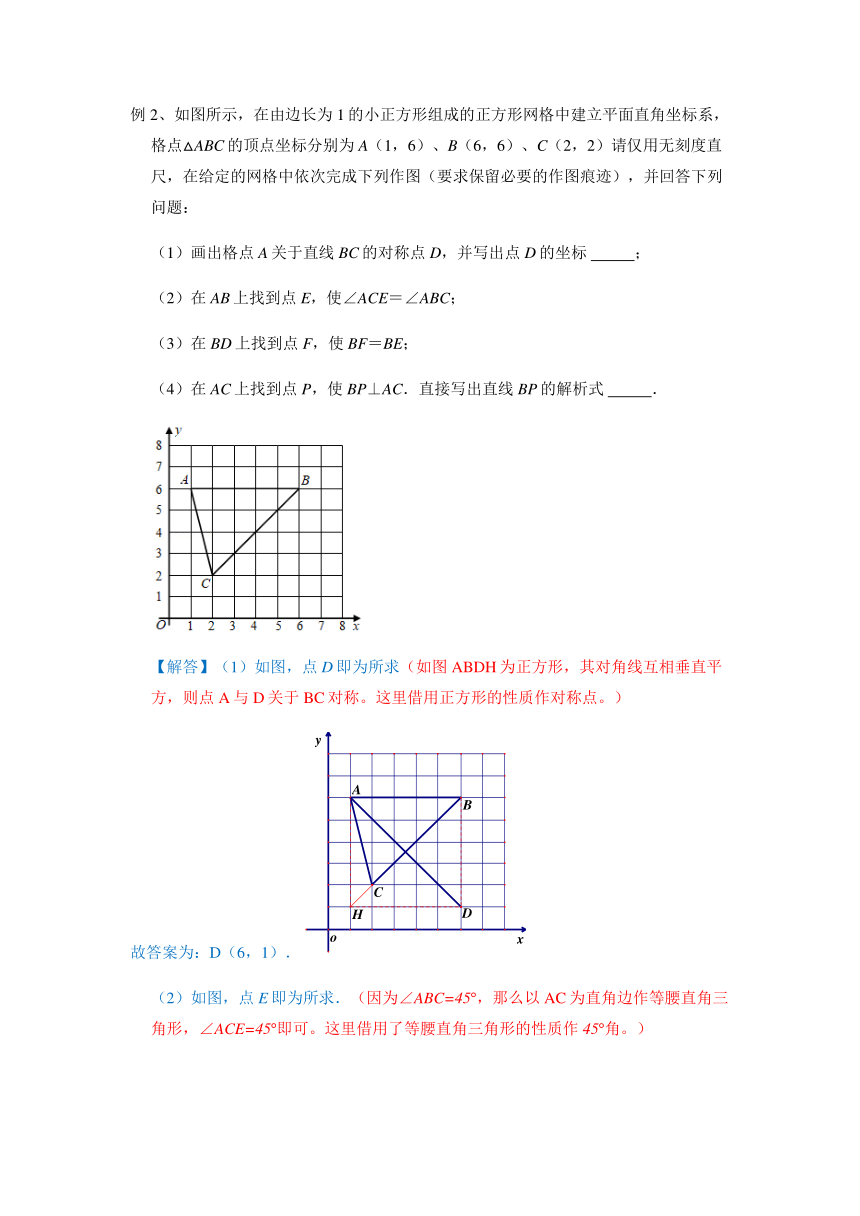
例2、如图所示,在由边长为1的小正方形组成的正方形网格中建立平面直角坐标系,格点△ABC的顶点坐标分别为A(1,6)、B(6,6)、C(2,2)请仅用无刻度直尺,在给定的网格中依次完成下列作图(要求保留必要的作图痕迹),并回答下列问题:
(1)画出格点A关于直线BC的对称点D,并写出点D的坐标 ;
(2)在AB上找到点E,使∠ACE=∠ABC;
(3)在BD上找到点F,使BF=BE;
(4)在AC上找到点P,使BP⊥AC.直接写出直线BP的解析式 .
【解答】(1)如图,点D即为所求(如图ABDH为正方形,其对角线互相垂直平方,则点A与D关于BC对称。这里借用正方形的性质作对称点。)
故答案为:D(6,1).
(2)如图,点E即为所求.(因为∠ABC=45,那么以AC为直角边作等腰直角三角形,∠ACE=45即可。这里借用了等腰直角三角形的性质作45角。)
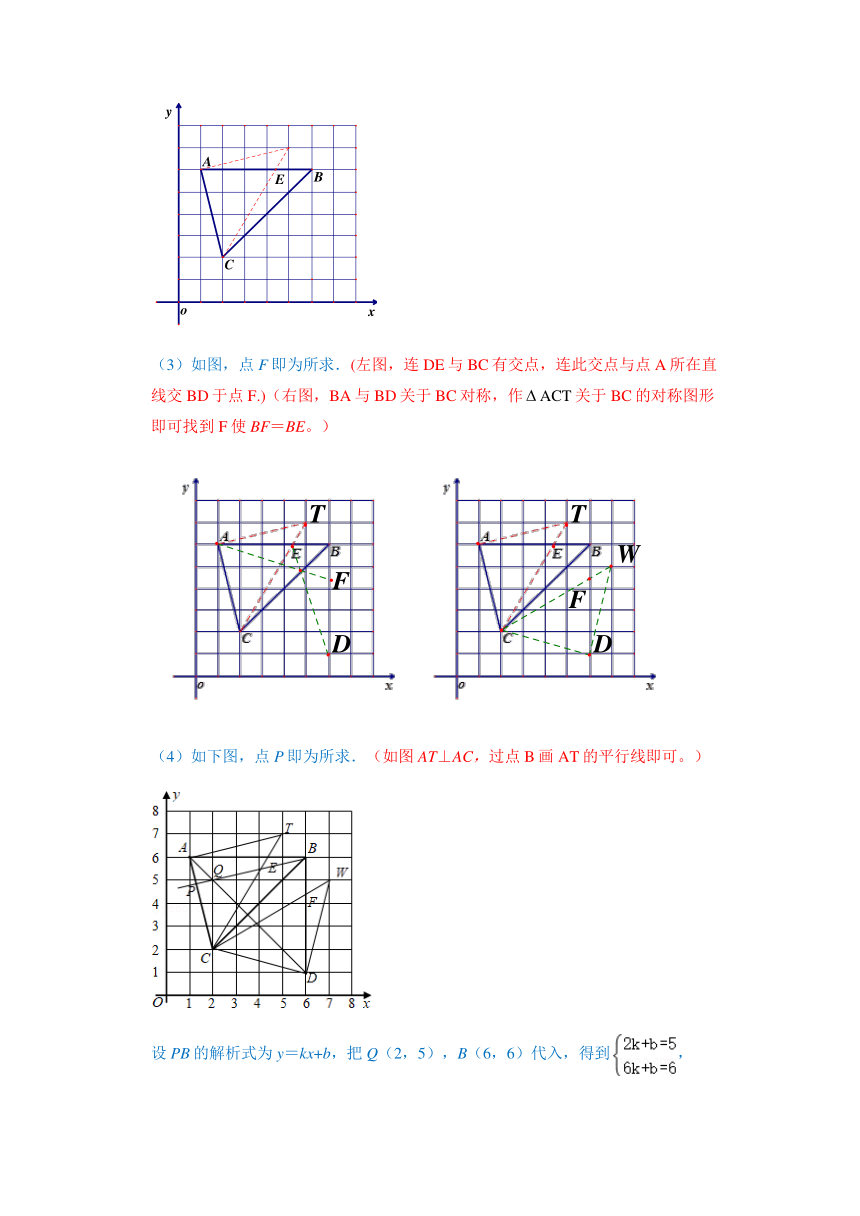
(3)如图,点F即为所求.(左图,连DE与BC有交点,连此交点与点A所在直线交BD于点F.)(右图,BA与BD关于BC对称,作ACT关于BC的对称图形即可找到F使BF=BE。)
(4)如下图,点P即为所求.(如图AT⊥AC,过点B画AT的平行线即可。)
设PB的解析式为y=kx+b,把Q(2,5),B(6,6)代入,得到,
解得,
∴直线BP的解析式为y=x+.
故答案为:y=x+.
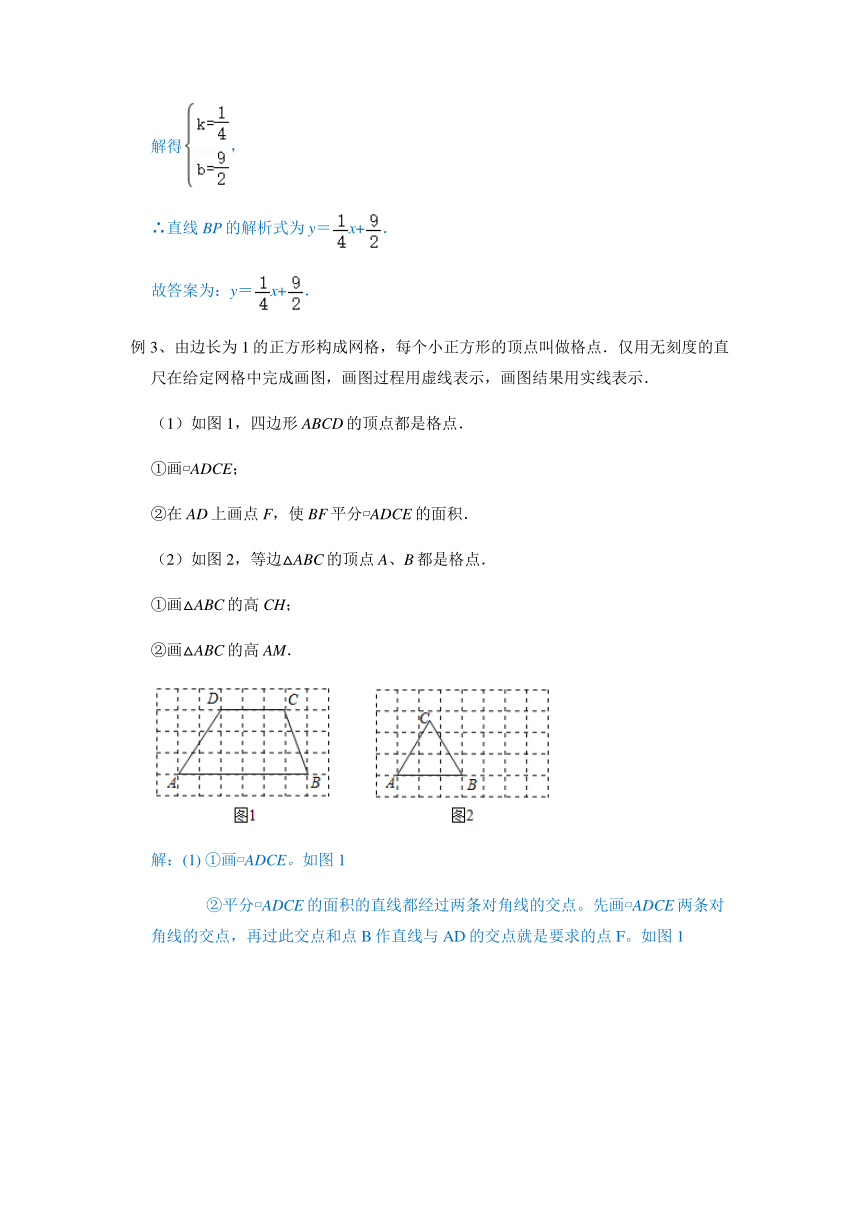
例3、由边长为1的正方形构成网格,每个小正方形的顶点叫做格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,画图结果用实线表示.
(1)如图1,四边形ABCD的顶点都是格点.
①画 ADCE;
②在AD上画点F,使BF平分 ADCE的面积.
(2)如图2,等边△ABC的顶点A、B都是格点.
①画△ABC的高CH;
②画△ABC的高AM.
解:(1) ①画 ADCE。如图1
②平分 ADCE的面积的直线都经过两条对角线的交点。先画 ADCE两条对角线的交点,再过此交点和点B作直线与AD的交点就是要求的点F。如图1
(2) ①先找AB的中点H,再画△ABC的高CH。如图2
②先作HB的垂直平分线,与BC的交点即为BC的中点M。再画△ABC的高AM.如图2
例4、如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,矩形的四个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图(1)中,先在边上画点,使,再过点画直线,使平分矩形的面积;
(2)在图(2)中,先画的高,再在边上画点,使.
【解】
(1)画图如图(1)
过点沿方向取一点,使得,得找到点,再连接矩形的对角线交点即可.
(2)画图如图(2)
画的高,步骤如下:
如图,连接M,N(M,N都是格点上的点)交网格线于I,
则,
中,
在中,
,
即
在边上画点,使,
步骤如下:如图,方法同上,找
可得:,
,为的中点,所以,即FY为BD的垂直平分线,FY交边于,即为所求点.
例5、在如图所示的网格中建立平面直角坐标系,的顶点坐标分别为,,,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,并回答下列问题:
(1)的形状为______;
(2)画出边上的高;
(3)画出点关于的对称点;
(4)已知点,点在线段上,若,则点的坐标为______.
解:
(1)为直角三角形
(2)找全等三角形得交点D即为垂足。
(3)延长AB到K,使AB=BK.作BC的平行线KL交垂线AD于点E.即为所求。
(4)左图,以AC为直角边作等腰直角三角形ACQ,过M作AQ的平行线交AC于点N即为所求。或,右图,作正方形ABRS,过点M作AR的平行线交AC于点N即为所求。
例6、如图是由小正方形组成的8×10网格,每个小正方形的顶点叫做格点,△ABC的三个顶点都是格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
在图(1)中,先在边BC上画点E,使BE=,再过点E画直线EF,
使EF∥AC;
(2)在图(2)中,先在边AC上画点D,使DB⊥AC,在直线BD上画点M,使点B与点M关于AC对称.
解:(1)BC=,那么点E为BC的中点。
(2)左图,,AC与BQ垂直,交点为D.
右图,延长BC至S使BC=CS,过点S作AC的平行线交BD于点M.即为所求。
例7、如图,点、、均为格点,请用无刻度直尺完成作图,画图过程用虚线,画图结果用实线表示,请按步骤完成下列问题.
在的下方找一个格点,使得为等腰直角三角形,且;
(2)在边上找一点,使;
(3)将线段向右平移2个单位得线段.
解:(1)如图,为等腰直角三角形。
(2)以AB为直角边作等腰直角三角形ABF,过点C作FB的平行线CG交A B于点E.
(3)如图,CG、AB均右移2个单位相交于点N。
例8、如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图(1)中,,分别是边,与网格线的交点.先将点绕点旋转得到点,画出点,再在上画点,使;
(2)在图(2)中,是边上一点,.先将绕点逆时针旋转,得到线段,画出线段,再画点,使,两点关于直线对称.
解:(1)E为AC的中点,加倍延长BE至F,点F即为所求。
D为BA的三等分点,在CA上找到三等分点G,连接DG即可。
(2)左图,,BW⊥AC;加倍延长BC至V,过点V作AC的平行线,交直线BW于点H,连接AH,即为所求。
右图,连接BQ交AC于点K,连接BK并延长交AH于点Q,即为所求。
一、考点:
(1)轴对称的性质
(2)平行线分线段的性质
(3)垂直平分线的性质
(4)特殊三角形、四边形的性质
(5)三角形全等、相似的性质
(6)三角函数、勾股定理
二、考查:
( 1 ) 画线段的中点(或等分点)、画对称点
(2) 画45角,找点
(3) 画平行线、垂线(或线段的垂直平分线),找点
(4) 画三角形全等、画三角形相似,找点
(5) 画轴对称图形,找点
三、举例:
例1、在平面直角坐标系中,点A(0,1),B(5,1),C(8,5),D(3,5),E(2,1),仅用无刻度的直尺在给定的网格中完成画图,画图过程用虚线表示,并回答下列问题.
(1)四边形ABCD的形状为 ;
(2)在AD上找点F,使AF=AE;
(3)分别在CD上找点M,BC上找点N,使四边形EFMN为矩形;
(4)将△ACF沿某条直线翻折后,点A,C,F的对应点均落在四边形ABCD的边上,请直接写出该直线的解析式为 .
【解答】(1)∵AB=CD=5,AD==5,BC==5,
∴AD=DC=CB=AB=5,
∴四边形ABCD是菱形.
故答案为:菱形.
(2)如图,点F即为所求.(菱形ABCD是轴对称图形,这里充分运用轴对称的性质画图。点B-D对应, 点E-F对应,线段BE,DF的交点在对称轴上,线段DE,BF的交点也在对称轴上。先连DE与对称轴的交点J,也是BF与对称轴的交点,这样连BJ就能找到点F。)
(3)如图,四边形EFMN即为所求.(图中MP平行于DB即可找到点N.)
(4)△ACF沿菱形ABCD的对角线翻折后,点A,C,F的对应点均落在四边形ABCD的边上,
对角线的解析式为y=﹣2x+11或y=x+1.
故答案为:y=﹣2x+11或y=x+1.
例2、如图所示,在由边长为1的小正方形组成的正方形网格中建立平面直角坐标系,格点△ABC的顶点坐标分别为A(1,6)、B(6,6)、C(2,2)请仅用无刻度直尺,在给定的网格中依次完成下列作图(要求保留必要的作图痕迹),并回答下列问题:
(1)画出格点A关于直线BC的对称点D,并写出点D的坐标 ;
(2)在AB上找到点E,使∠ACE=∠ABC;
(3)在BD上找到点F,使BF=BE;
(4)在AC上找到点P,使BP⊥AC.直接写出直线BP的解析式 .
【解答】(1)如图,点D即为所求(如图ABDH为正方形,其对角线互相垂直平方,则点A与D关于BC对称。这里借用正方形的性质作对称点。)
故答案为:D(6,1).
(2)如图,点E即为所求.(因为∠ABC=45,那么以AC为直角边作等腰直角三角形,∠ACE=45即可。这里借用了等腰直角三角形的性质作45角。)
(3)如图,点F即为所求.(左图,连DE与BC有交点,连此交点与点A所在直线交BD于点F.)(右图,BA与BD关于BC对称,作ACT关于BC的对称图形即可找到F使BF=BE。)
(4)如下图,点P即为所求.(如图AT⊥AC,过点B画AT的平行线即可。)
设PB的解析式为y=kx+b,把Q(2,5),B(6,6)代入,得到,
解得,
∴直线BP的解析式为y=x+.
故答案为:y=x+.
例3、由边长为1的正方形构成网格,每个小正方形的顶点叫做格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,画图结果用实线表示.
(1)如图1,四边形ABCD的顶点都是格点.
①画 ADCE;
②在AD上画点F,使BF平分 ADCE的面积.
(2)如图2,等边△ABC的顶点A、B都是格点.
①画△ABC的高CH;
②画△ABC的高AM.
解:(1) ①画 ADCE。如图1
②平分 ADCE的面积的直线都经过两条对角线的交点。先画 ADCE两条对角线的交点,再过此交点和点B作直线与AD的交点就是要求的点F。如图1
(2) ①先找AB的中点H,再画△ABC的高CH。如图2
②先作HB的垂直平分线,与BC的交点即为BC的中点M。再画△ABC的高AM.如图2
例4、如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,矩形的四个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图(1)中,先在边上画点,使,再过点画直线,使平分矩形的面积;
(2)在图(2)中,先画的高,再在边上画点,使.
【解】
(1)画图如图(1)
过点沿方向取一点,使得,得找到点,再连接矩形的对角线交点即可.
(2)画图如图(2)
画的高,步骤如下:
如图,连接M,N(M,N都是格点上的点)交网格线于I,
则,
中,
在中,
,
即
在边上画点,使,
步骤如下:如图,方法同上,找
可得:,
,为的中点,所以,即FY为BD的垂直平分线,FY交边于,即为所求点.
例5、在如图所示的网格中建立平面直角坐标系,的顶点坐标分别为,,,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,并回答下列问题:
(1)的形状为______;
(2)画出边上的高;
(3)画出点关于的对称点;
(4)已知点,点在线段上,若,则点的坐标为______.
解:
(1)为直角三角形
(2)找全等三角形得交点D即为垂足。
(3)延长AB到K,使AB=BK.作BC的平行线KL交垂线AD于点E.即为所求。
(4)左图,以AC为直角边作等腰直角三角形ACQ,过M作AQ的平行线交AC于点N即为所求。或,右图,作正方形ABRS,过点M作AR的平行线交AC于点N即为所求。
例6、如图是由小正方形组成的8×10网格,每个小正方形的顶点叫做格点,△ABC的三个顶点都是格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
在图(1)中,先在边BC上画点E,使BE=,再过点E画直线EF,
使EF∥AC;
(2)在图(2)中,先在边AC上画点D,使DB⊥AC,在直线BD上画点M,使点B与点M关于AC对称.
解:(1)BC=,那么点E为BC的中点。
(2)左图,,AC与BQ垂直,交点为D.
右图,延长BC至S使BC=CS,过点S作AC的平行线交BD于点M.即为所求。
例7、如图,点、、均为格点,请用无刻度直尺完成作图,画图过程用虚线,画图结果用实线表示,请按步骤完成下列问题.
在的下方找一个格点,使得为等腰直角三角形,且;
(2)在边上找一点,使;
(3)将线段向右平移2个单位得线段.
解:(1)如图,为等腰直角三角形。
(2)以AB为直角边作等腰直角三角形ABF,过点C作FB的平行线CG交A B于点E.
(3)如图,CG、AB均右移2个单位相交于点N。
例8、如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图(1)中,,分别是边,与网格线的交点.先将点绕点旋转得到点,画出点,再在上画点,使;
(2)在图(2)中,是边上一点,.先将绕点逆时针旋转,得到线段,画出线段,再画点,使,两点关于直线对称.
解:(1)E为AC的中点,加倍延长BE至F,点F即为所求。
D为BA的三等分点,在CA上找到三等分点G,连接DG即可。
(2)左图,,BW⊥AC;加倍延长BC至V,过点V作AC的平行线,交直线BW于点H,连接AH,即为所求。
右图,连接BQ交AC于点K,连接BK并延长交AH于点Q,即为所求。
同课章节目录
