2024 年人教版中考数学 测试卷5 圆(含答案)
文档属性
| 名称 | 2024 年人教版中考数学 测试卷5 圆(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 329.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 18:37:24 | ||
图片预览

文档简介
测试卷五 圆
(说明:共有三个大题,26个小题,满分120分,作答时间120分钟)
中考对接点:圆的有关性质,点与圆、直线与圆的位置关系,与圆有关的计算,正多边形与圆,三角形的外心和内心,圆与特殊多边形的相关证明与计算
题号 一 二 三 总分 累分人
得分
一、选择题(本大题共16个小题.1~10小题每题3分,11~16小题每题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知☉O的半径是4,OP=5,则点P与☉O的位置关系是( )
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定
2.在☉O中,直径AB=a,弦CD=b,则a与b的大小关系为( )
A.a>b B.a≥b C.a3.如图,AB是☉O的直径,C为圆内一点,则下列说法正确的是( )
A.AC是☉O的弦 B.∠BOC是圆周角 C.∠C是圆周角 D.AB是☉O的弦
4.如图,点A,点B,点C都在☉O上,且∠AOC=140°,则∠B的度数为( )
A.70° B.100° C.110° D.120°
5.如图,AB为☉O的切线,OB交☉O于点C,D为☉O上一点,若∠ADC=24°,则∠ABO的度数为( )
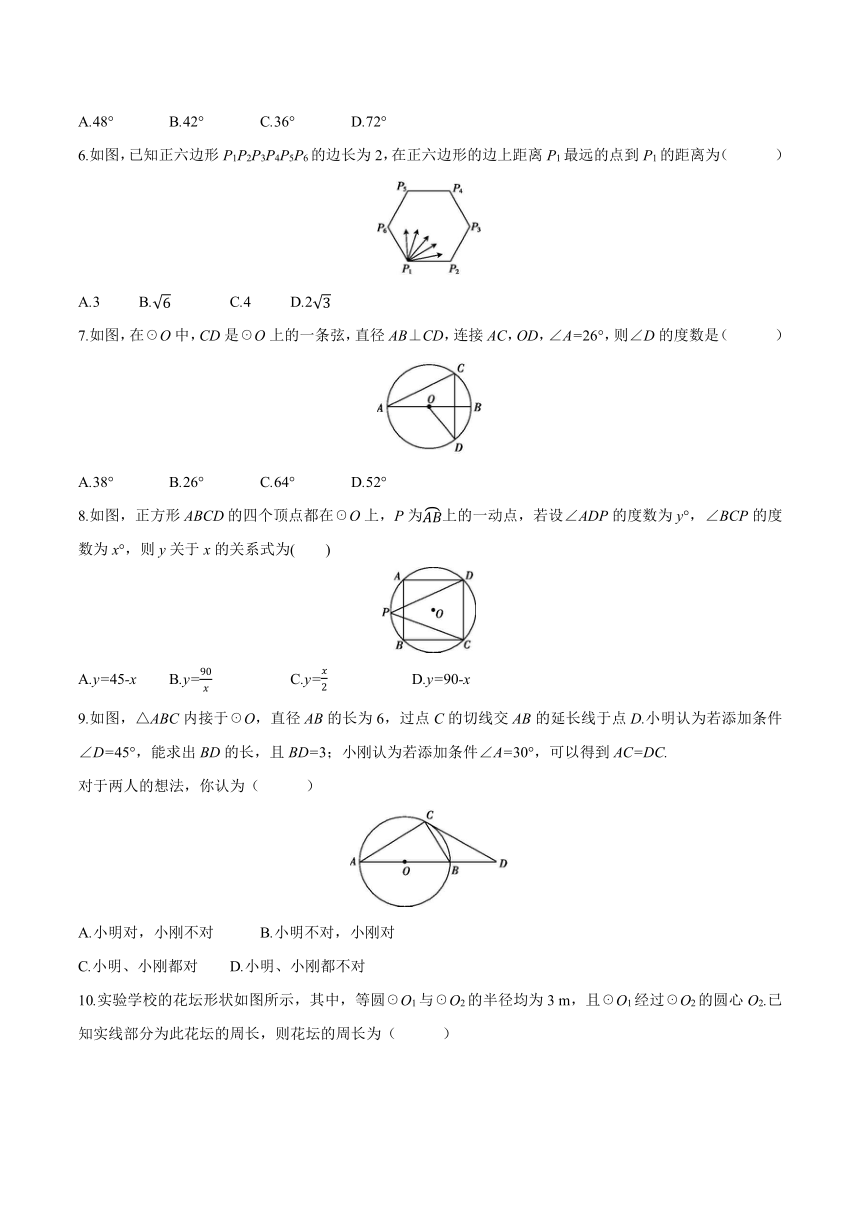
A.48° B.42° C.36° D.72°
6.如图,已知正六边形P1P2P3P4P5P6的边长为2,在正六边形的边上距离P1最远的点到P1的距离为( )
A.3 B. C.4 D.2
7.如图,在☉O中,CD是☉O上的一条弦,直径AB⊥CD,连接AC,OD,∠A=26°,则∠D的度数是( )
A.38° B.26° C.64° D.52°
8.如图,正方形ABCD的四个顶点都在☉O上,P为上的一动点,若设∠ADP的度数为y°,∠BCP的度数为x°,则y关于x的关系式为( )
A.y=45-x B.y= C.y= D.y=90-x
9.如图,△ABC内接于☉O,直径AB的长为6,过点C的切线交AB的延长线于点D.小明认为若添加条件∠D=45°,能求出BD的长,且BD=3;小刚认为若添加条件∠A=30°,可以得到AC=DC.
对于两人的想法,你认为( )
A.小明对,小刚不对 B.小明不对,小刚对
C.小明、小刚都对 D.小明、小刚都不对
10.实验学校的花坛形状如图所示,其中,等圆☉O1与☉O2的半径均为3 m,且☉O1经过☉O2的圆心O2.已知实线部分为此花坛的周长,则花坛的周长为( )
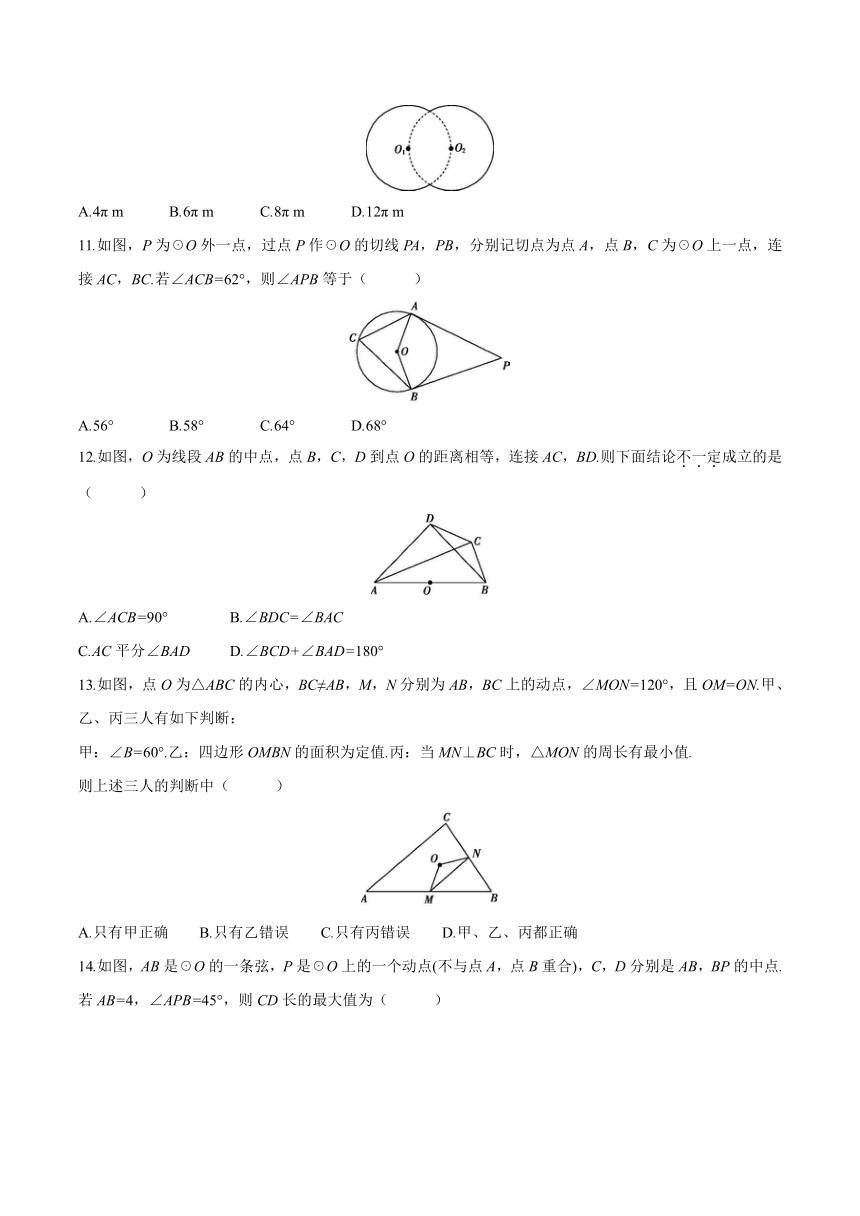
A.4π m B.6π m C.8π m D.12π m
11.如图,P为☉O外一点,过点P作☉O的切线PA,PB,分别记切点为点A,点B,C为☉O上一点,连接AC,BC.若∠ACB=62°,则∠APB等于( )
A.56° B.58° C.64° D.68°
12.如图,O为线段AB的中点,点B,C,D到点O的距离相等,连接AC,BD.则下面结论不一定成立的是( )
A.∠ACB=90° B.∠BDC=∠BAC
C.AC平分∠BAD D.∠BCD+∠BAD=180°
13.如图,点O为△ABC的内心,BC≠AB,M,N分别为AB,BC上的动点,∠MON=120°,且OM=ON.甲、乙、丙三人有如下判断:
甲:∠B=60°.乙:四边形OMBN的面积为定值.丙:当MN⊥BC时,△MON的周长有最小值.
则上述三人的判断中( )
A.只有甲正确 B.只有乙错误 C.只有丙错误 D.甲、乙、丙都正确
14.如图,AB是☉O的一条弦,P是☉O上的一个动点(不与点A,点B重合),C,D分别是AB,BP的中点.若AB=4,∠APB=45°,则CD长的最大值为( )
A.2 B.2 C.4 D.4
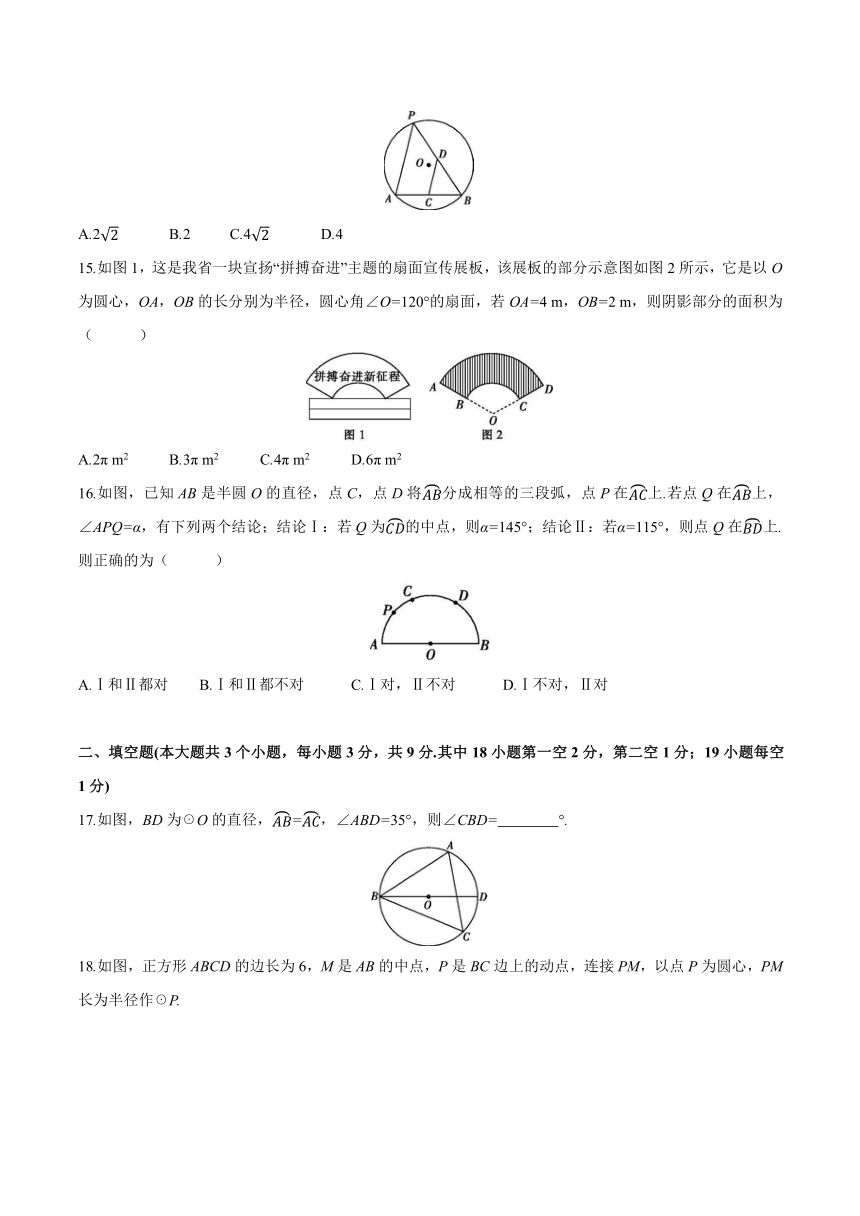
15.如图1,这是我省一块宣扬“拼搏奋进”主题的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB的长分别为半径,圆心角∠O=120°的扇面,若OA=4 m,OB=2 m,则阴影部分的面积为( )
A.2π m2 B.3π m2 C.4π m2 D.6π m2
16.如图,已知AB是半圆O的直径,点C,点D将分成相等的三段弧,点P在上.若点Q在上,∠APQ=α,有下列两个结论;结论Ⅰ:若Q为的中点,则α=145°;结论Ⅱ:若α=115°,则点Q在上.
则正确的为( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ对,Ⅱ不对 D.Ⅰ不对,Ⅱ对
二、填空题(本大题共3个小题,每小题3分,共9分.其中18小题第一空2分,第二空1分;19小题每空1分)
17.如图,BD为☉O的直径,=,∠ABD=35°,则∠CBD= °.
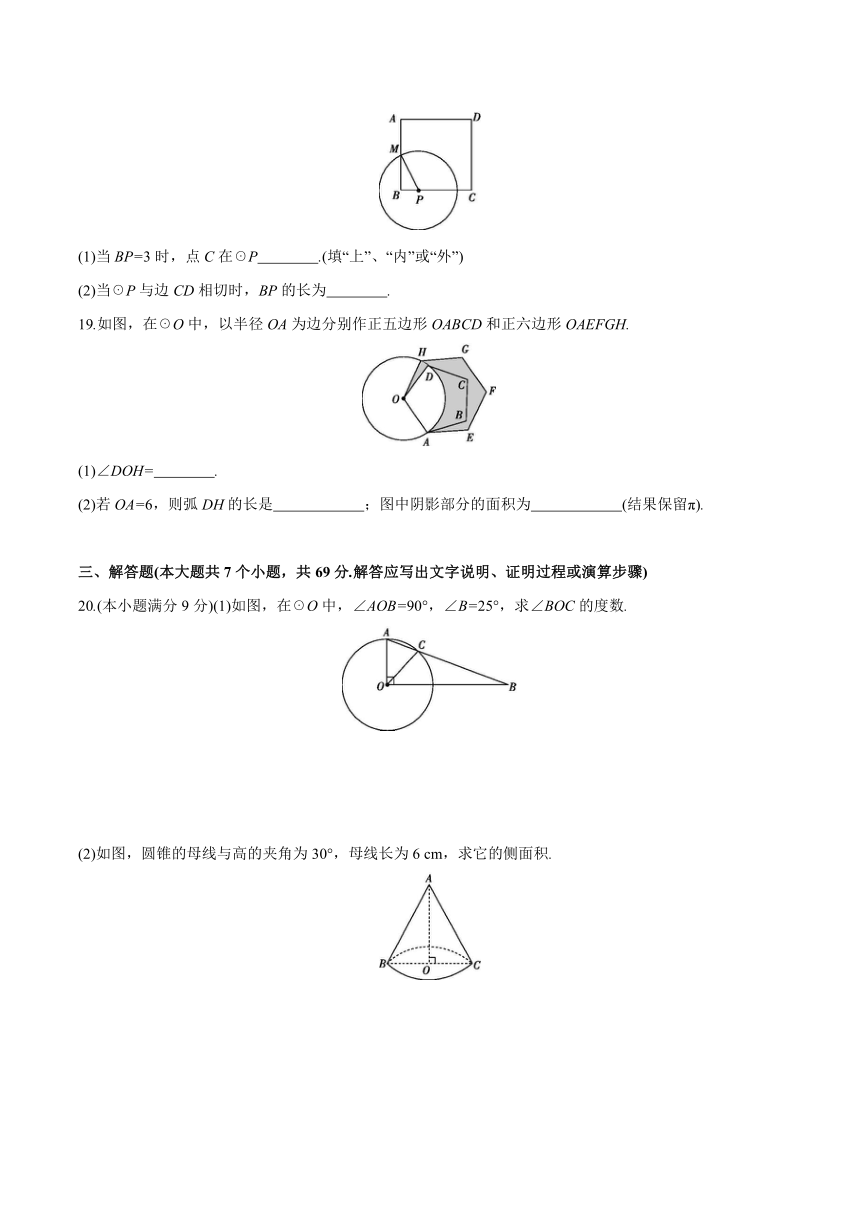
18.如图,正方形ABCD的边长为6,M是AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作☉P.
(1)当BP=3时,点C在☉P .(填“上”、“内”或“外”)
(2)当☉P与边CD相切时,BP的长为 .
19.如图,在☉O中,以半径OA为边分别作正五边形OABCD和正六边形OAEFGH.
(1)∠DOH= .
(2)若OA=6,则弧DH的长是 ;图中阴影部分的面积为 (结果保留π).
三、解答题(本大题共7个小题,共69分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)(1)如图,在☉O中,∠AOB=90°,∠B=25°,求∠BOC的度数.
(2)如图,圆锥的母线与高的夹角为30°,母线长为6 cm,求它的侧面积.
21.(本小题满分9分)如图,在△ABC中,以AB为直径的☉O与AC,BC的交点分别为D,E.
(1)若∠A=65°,求∠CED的大小.
(2)若DE=BE,求证:△ABC为等腰三角形.
22.(本小题满分9分)如图,已知P为反比例函数y=(x>0)图象上一点,以点P为圆心,OP的长为半径画圆,☉P与x轴相交于点A,且点A的坐标为(4,0).
(1)求☉P的半径.
(2)求图中阴影部分的面积.
23.(本小题满分10分)如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于点O,D为AB上的一点,OD=OC,以点O为圆心,OB的长为半径作☉O.已知AB=8,BD=2.
(1)求证:AC是☉O的切线.
(2)求线段AC的长.
24.(本小题满分10分)已知:在☉O中,AB为直径,P为射线AB上一点,过点P作☉O的切线,切点为点C,D为上一点,连接BD,BC,DC.
(1)如图1,求证:∠D=∠PCB.
(2)如图2,若四边形CDBP为平行四边形,BC=6,求☉O的半径.
25.(本小题满分10分)如图,△ABC内接于☉O,且AB为☉O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是☉O的切线.
(2)求证:∠B=∠ACD.
(3)若OD=5,CD=3,求BC的长.
26.(本小题满分12分)
问题提出
(1)如图1,☉O的半径为6,弦AB=6,则点O到AB的距离是 .
问题探究
(2)如图2,☉O的半径为10,点A,B,C都在☉O上,AB=16,求△ABC面积的最大值.
问题解决
(3)如图3,这是一圆形景观区示意图,☉O的直径为60 m,等腰直角△ABP的边AB是☉O的弦,直角顶点P在☉O内,延长AP交☉O于点C,延长BP交☉O于点D,连接CD,AD,BC.现准备在△ABP和△CDP区域内种植草坪,在△ADP和△BCP区域内种植花卉.记△ABP和△CDP的面积和为S1,△ADP和△BCP的面积和为S2.
①求种植草坪的区域面积S1;
②求种植花卉的区域面积S2的最大值.(提示:(a±b)2=a2±2ab+b2≥0)
参考答案 (五)
1.C 2.B 3.D 4.C 5.B 6.C 7.A 8.A 9.B 10.C 11.A 12.C 13.C 14.A 15.C
16.D
提示:结论Ⅰ:如图,∵C,D是半圆的三等分点,Q是的中点,∴=,∴∠AOQ=∠BOQ=×180°=90°,
∴∠ABQ=∠AOQ=×90°=45°.
∵四边形APQB是圆内接四边形,
∴∠APQ=180°-45°=135°,因此结论Ⅰ不正确.
结论Ⅱ:当α=115°时,即∠APQ=115°,因此有∠ABQ=180°-115°=65°,
而∠ABD=×120°=60°,∴点Q在上,因此结论Ⅱ正确.故选D.
17.20
18.(1)内 (2)
19.(1)12° (2);54-
20.(1)解:∵∠AOB=90°,∠B=25°,
∴∠A=90°-∠B=90°-25°=65°. 1分
∵OA=OC,
∴∠ACO=∠A=65°, 2分
而∠ACO=∠BOC+∠B,
∴∠BOC=65°-25°=40°. 4分
(2)解:∵圆锥的母线与高的夹角为30°,母线长为6 cm,
∴圆锥的底面圆的半径=6sin 30°=3 cm, 6分
∴它的侧面积=×2π×3×6=18π cm2. 9分
21.解:(1)∵∠A+∠BED=180°,∠DEB+∠CED=180°,
∴∠CED=∠A=65°. 3分
(2)证明:∵AB为☉O的直径,
∴∠ADB=90°.
∵ED=EB,
∴∠EDB=∠EBD.
∵∠CDE+∠EDB=90°,∠C+∠EBD=90°,
∴∠C=∠CDE. 6分
∵∠CDE+∠ADE=180°,∠ABC+∠ADE=180°,
∴∠CDE=∠ABC,
∴∠C=∠ABC,
∴△ABC为等腰三角形. 9分
22.解:(1)如图,过点P作PD⊥x轴. 1分
可得OD=2.
将x=2代入y=,可得y=2.
在Rt△OPD中,据勾股定理可得OP=4. 4分
(2)∵=,
∴∠OPD=60°,即∠OPA=120°, 6分
∴S阴影=S扇形OPA-S△OPA=-4=-4. 9分
23.解:(1)(解法不唯一)证明:如图,过点O作OF⊥AC于点F, 1分
∴∠AFO=∠ABC=90°.
∵AO平分∠BAC,AO=AO,
∴△ABO≌△AFO, 3分
∴OF=OB,
∴OF是☉O的半径,
∴AC是☉O的切线. 5分
(2)在Rt△BOD和Rt△FOC中,
∴Rt△BOD≌Rt△FOC(HL), 7分
∴FC=BD=2.
∵AF=AB=8(切线长相等),
∴AC=AF+FC=8+2=10. 10分
24.
解:(1)证明:如图1连接AC,OC. 1分
∵AB是☉O的直径,PC为☉O的切线,
∴∠ACB=∠OCP=90°,
∴∠ACO=∠PCB.
∵OA=OC,∴∠ACO=∠A.
∵∠A=∠D(同弧所对圆周角相等),
∴∠D=∠PCB. 4分
(2)如图2,连接AC,OC.
∵四边形CDBP为平行四边形,
∴∠D=∠CPB. 5分
由(1)得∠ACB=∠OCP=90°,∠D=∠A,
∴∠D=∠A=∠CPB=∠PCB. 6分
在△ACP中,∠A+∠ACB+∠BCP+∠CPB=180°,
∴∠A+∠BCP+∠CPB=90°,
∴∠A=∠CPB=∠PCB=30°,
∴∠OBC=60°.
∵OB=OC,
∴△OBC是等边三角形,
∴OB=BC=6,
故☉O的半径为6. 10分
25.解:(1)证明:如图,连接OC,则OA=OC, 1分
∴∠A=∠ACO,
∴∠BOC=∠A+∠ACO=2∠A.
∵OD⊥AB,∴∠DOC+∠BOC=90°.
又∵∠D=2∠A,∴∠D+∠DOC=90°,
∴∠DCO=90°,
∴CD是☉O的切线. 3分
(2)证明:∵AB是☉O的直径,∴∠ACB=90°. 4分
由(1)知∠OCD=90°.
∵∠A=∠ACO,∴∠B=∠ACD. 6分
(3)∵∠EAO=∠BAC,∠AOE=∠ACB=90°,
∴△AOE∽△ACB,∴∠B=∠AEO. 7分
∵∠B=∠ACD,∠AEO=∠DEC,
∴∠DCE=∠DEC,
∴DE=CD=3.
又∵OD=5,∴OE=2,OC=4,∴AE==2. 8分
由△AOE∽△ACB得=,
∴=,∴BC=. 10分
26.解:(1)3. 2分
提示:如图1,连接AO,BO,过点O作OH⊥AB于点H.
∵OA=OB=6,AB=6,OH⊥BA,
∴AH=3,
∴OH===3,
∴点O到AB的距离是3.
(2)∵S△ABC=×AB×h(点C到AB的距离),且AB的长是定值,
∴当点C到AB的距离最大时,△ABC的面积有最大值. 4分
如图2,过点O作OE⊥AB于点E,当E,O,C'三点共线时,点C'到AB的距离最大,
∴AE=BE=8.
∵☉O的半径为10.
∴OE===6. 6分
当E,O,C'三点共线,即EC'=10+6=16时,△ABC的面积最大,
∴△ABC的面积最大值=×16×16=128. 7分
(3)①如图3,连接AO,DO.
∵△ABP是等腰直角三角形,
∴∠ABP=∠BAP=45°,∠APB=∠CPD=90°,
∴∠AOD=2∠ABD=90°,∠ACD=∠ABP=45°,∠BDC=∠CAB=45°,
∴△AOD是等腰直角三角形,△DPC是等腰直角三角形. 9分
∵☉O的直径为60 m,
∴AO=DO=30 m.
∵AD2=AO2+DO2=DP2+AP2=1800,S△ABP=AP2,S△CDP=DP2,
∴S△ABP+S△CDP=(AP2+DP2)=900(m2),
∴S1=900 m2. 10分
②∵S△ADP=×AP×DP,S△BCP=×CP×BP,∴S2=S△ADP+S△BCP=AP×DP.
∵(AP-DP)2≥0,
∴AP2+DP2≥2AP×DP.
∵DP2+AP2=1800,
∴S2=AP×DP≤900,
∴S2的最大值为900 m2. 12分
(说明:共有三个大题,26个小题,满分120分,作答时间120分钟)
中考对接点:圆的有关性质,点与圆、直线与圆的位置关系,与圆有关的计算,正多边形与圆,三角形的外心和内心,圆与特殊多边形的相关证明与计算
题号 一 二 三 总分 累分人
得分
一、选择题(本大题共16个小题.1~10小题每题3分,11~16小题每题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知☉O的半径是4,OP=5,则点P与☉O的位置关系是( )
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定
2.在☉O中,直径AB=a,弦CD=b,则a与b的大小关系为( )
A.a>b B.a≥b C.a3.如图,AB是☉O的直径,C为圆内一点,则下列说法正确的是( )
A.AC是☉O的弦 B.∠BOC是圆周角 C.∠C是圆周角 D.AB是☉O的弦
4.如图,点A,点B,点C都在☉O上,且∠AOC=140°,则∠B的度数为( )
A.70° B.100° C.110° D.120°
5.如图,AB为☉O的切线,OB交☉O于点C,D为☉O上一点,若∠ADC=24°,则∠ABO的度数为( )
A.48° B.42° C.36° D.72°
6.如图,已知正六边形P1P2P3P4P5P6的边长为2,在正六边形的边上距离P1最远的点到P1的距离为( )
A.3 B. C.4 D.2
7.如图,在☉O中,CD是☉O上的一条弦,直径AB⊥CD,连接AC,OD,∠A=26°,则∠D的度数是( )
A.38° B.26° C.64° D.52°
8.如图,正方形ABCD的四个顶点都在☉O上,P为上的一动点,若设∠ADP的度数为y°,∠BCP的度数为x°,则y关于x的关系式为( )
A.y=45-x B.y= C.y= D.y=90-x
9.如图,△ABC内接于☉O,直径AB的长为6,过点C的切线交AB的延长线于点D.小明认为若添加条件∠D=45°,能求出BD的长,且BD=3;小刚认为若添加条件∠A=30°,可以得到AC=DC.
对于两人的想法,你认为( )
A.小明对,小刚不对 B.小明不对,小刚对
C.小明、小刚都对 D.小明、小刚都不对
10.实验学校的花坛形状如图所示,其中,等圆☉O1与☉O2的半径均为3 m,且☉O1经过☉O2的圆心O2.已知实线部分为此花坛的周长,则花坛的周长为( )
A.4π m B.6π m C.8π m D.12π m
11.如图,P为☉O外一点,过点P作☉O的切线PA,PB,分别记切点为点A,点B,C为☉O上一点,连接AC,BC.若∠ACB=62°,则∠APB等于( )
A.56° B.58° C.64° D.68°
12.如图,O为线段AB的中点,点B,C,D到点O的距离相等,连接AC,BD.则下面结论不一定成立的是( )
A.∠ACB=90° B.∠BDC=∠BAC
C.AC平分∠BAD D.∠BCD+∠BAD=180°
13.如图,点O为△ABC的内心,BC≠AB,M,N分别为AB,BC上的动点,∠MON=120°,且OM=ON.甲、乙、丙三人有如下判断:
甲:∠B=60°.乙:四边形OMBN的面积为定值.丙:当MN⊥BC时,△MON的周长有最小值.
则上述三人的判断中( )
A.只有甲正确 B.只有乙错误 C.只有丙错误 D.甲、乙、丙都正确
14.如图,AB是☉O的一条弦,P是☉O上的一个动点(不与点A,点B重合),C,D分别是AB,BP的中点.若AB=4,∠APB=45°,则CD长的最大值为( )
A.2 B.2 C.4 D.4
15.如图1,这是我省一块宣扬“拼搏奋进”主题的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB的长分别为半径,圆心角∠O=120°的扇面,若OA=4 m,OB=2 m,则阴影部分的面积为( )
A.2π m2 B.3π m2 C.4π m2 D.6π m2
16.如图,已知AB是半圆O的直径,点C,点D将分成相等的三段弧,点P在上.若点Q在上,∠APQ=α,有下列两个结论;结论Ⅰ:若Q为的中点,则α=145°;结论Ⅱ:若α=115°,则点Q在上.
则正确的为( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ对,Ⅱ不对 D.Ⅰ不对,Ⅱ对
二、填空题(本大题共3个小题,每小题3分,共9分.其中18小题第一空2分,第二空1分;19小题每空1分)
17.如图,BD为☉O的直径,=,∠ABD=35°,则∠CBD= °.
18.如图,正方形ABCD的边长为6,M是AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作☉P.
(1)当BP=3时,点C在☉P .(填“上”、“内”或“外”)
(2)当☉P与边CD相切时,BP的长为 .
19.如图,在☉O中,以半径OA为边分别作正五边形OABCD和正六边形OAEFGH.
(1)∠DOH= .
(2)若OA=6,则弧DH的长是 ;图中阴影部分的面积为 (结果保留π).
三、解答题(本大题共7个小题,共69分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)(1)如图,在☉O中,∠AOB=90°,∠B=25°,求∠BOC的度数.
(2)如图,圆锥的母线与高的夹角为30°,母线长为6 cm,求它的侧面积.
21.(本小题满分9分)如图,在△ABC中,以AB为直径的☉O与AC,BC的交点分别为D,E.
(1)若∠A=65°,求∠CED的大小.
(2)若DE=BE,求证:△ABC为等腰三角形.
22.(本小题满分9分)如图,已知P为反比例函数y=(x>0)图象上一点,以点P为圆心,OP的长为半径画圆,☉P与x轴相交于点A,且点A的坐标为(4,0).
(1)求☉P的半径.
(2)求图中阴影部分的面积.
23.(本小题满分10分)如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于点O,D为AB上的一点,OD=OC,以点O为圆心,OB的长为半径作☉O.已知AB=8,BD=2.
(1)求证:AC是☉O的切线.
(2)求线段AC的长.
24.(本小题满分10分)已知:在☉O中,AB为直径,P为射线AB上一点,过点P作☉O的切线,切点为点C,D为上一点,连接BD,BC,DC.
(1)如图1,求证:∠D=∠PCB.
(2)如图2,若四边形CDBP为平行四边形,BC=6,求☉O的半径.
25.(本小题满分10分)如图,△ABC内接于☉O,且AB为☉O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是☉O的切线.
(2)求证:∠B=∠ACD.
(3)若OD=5,CD=3,求BC的长.
26.(本小题满分12分)
问题提出
(1)如图1,☉O的半径为6,弦AB=6,则点O到AB的距离是 .
问题探究
(2)如图2,☉O的半径为10,点A,B,C都在☉O上,AB=16,求△ABC面积的最大值.
问题解决
(3)如图3,这是一圆形景观区示意图,☉O的直径为60 m,等腰直角△ABP的边AB是☉O的弦,直角顶点P在☉O内,延长AP交☉O于点C,延长BP交☉O于点D,连接CD,AD,BC.现准备在△ABP和△CDP区域内种植草坪,在△ADP和△BCP区域内种植花卉.记△ABP和△CDP的面积和为S1,△ADP和△BCP的面积和为S2.
①求种植草坪的区域面积S1;
②求种植花卉的区域面积S2的最大值.(提示:(a±b)2=a2±2ab+b2≥0)
参考答案 (五)
1.C 2.B 3.D 4.C 5.B 6.C 7.A 8.A 9.B 10.C 11.A 12.C 13.C 14.A 15.C
16.D
提示:结论Ⅰ:如图,∵C,D是半圆的三等分点,Q是的中点,∴=,∴∠AOQ=∠BOQ=×180°=90°,
∴∠ABQ=∠AOQ=×90°=45°.
∵四边形APQB是圆内接四边形,
∴∠APQ=180°-45°=135°,因此结论Ⅰ不正确.
结论Ⅱ:当α=115°时,即∠APQ=115°,因此有∠ABQ=180°-115°=65°,
而∠ABD=×120°=60°,∴点Q在上,因此结论Ⅱ正确.故选D.
17.20
18.(1)内 (2)
19.(1)12° (2);54-
20.(1)解:∵∠AOB=90°,∠B=25°,
∴∠A=90°-∠B=90°-25°=65°. 1分
∵OA=OC,
∴∠ACO=∠A=65°, 2分
而∠ACO=∠BOC+∠B,
∴∠BOC=65°-25°=40°. 4分
(2)解:∵圆锥的母线与高的夹角为30°,母线长为6 cm,
∴圆锥的底面圆的半径=6sin 30°=3 cm, 6分
∴它的侧面积=×2π×3×6=18π cm2. 9分
21.解:(1)∵∠A+∠BED=180°,∠DEB+∠CED=180°,
∴∠CED=∠A=65°. 3分
(2)证明:∵AB为☉O的直径,
∴∠ADB=90°.
∵ED=EB,
∴∠EDB=∠EBD.
∵∠CDE+∠EDB=90°,∠C+∠EBD=90°,
∴∠C=∠CDE. 6分
∵∠CDE+∠ADE=180°,∠ABC+∠ADE=180°,
∴∠CDE=∠ABC,
∴∠C=∠ABC,
∴△ABC为等腰三角形. 9分
22.解:(1)如图,过点P作PD⊥x轴. 1分
可得OD=2.
将x=2代入y=,可得y=2.
在Rt△OPD中,据勾股定理可得OP=4. 4分
(2)∵=,
∴∠OPD=60°,即∠OPA=120°, 6分
∴S阴影=S扇形OPA-S△OPA=-4=-4. 9分
23.解:(1)(解法不唯一)证明:如图,过点O作OF⊥AC于点F, 1分
∴∠AFO=∠ABC=90°.
∵AO平分∠BAC,AO=AO,
∴△ABO≌△AFO, 3分
∴OF=OB,
∴OF是☉O的半径,
∴AC是☉O的切线. 5分
(2)在Rt△BOD和Rt△FOC中,
∴Rt△BOD≌Rt△FOC(HL), 7分
∴FC=BD=2.
∵AF=AB=8(切线长相等),
∴AC=AF+FC=8+2=10. 10分
24.
解:(1)证明:如图1连接AC,OC. 1分
∵AB是☉O的直径,PC为☉O的切线,
∴∠ACB=∠OCP=90°,
∴∠ACO=∠PCB.
∵OA=OC,∴∠ACO=∠A.
∵∠A=∠D(同弧所对圆周角相等),
∴∠D=∠PCB. 4分
(2)如图2,连接AC,OC.
∵四边形CDBP为平行四边形,
∴∠D=∠CPB. 5分
由(1)得∠ACB=∠OCP=90°,∠D=∠A,
∴∠D=∠A=∠CPB=∠PCB. 6分
在△ACP中,∠A+∠ACB+∠BCP+∠CPB=180°,
∴∠A+∠BCP+∠CPB=90°,
∴∠A=∠CPB=∠PCB=30°,
∴∠OBC=60°.
∵OB=OC,
∴△OBC是等边三角形,
∴OB=BC=6,
故☉O的半径为6. 10分
25.解:(1)证明:如图,连接OC,则OA=OC, 1分
∴∠A=∠ACO,
∴∠BOC=∠A+∠ACO=2∠A.
∵OD⊥AB,∴∠DOC+∠BOC=90°.
又∵∠D=2∠A,∴∠D+∠DOC=90°,
∴∠DCO=90°,
∴CD是☉O的切线. 3分
(2)证明:∵AB是☉O的直径,∴∠ACB=90°. 4分
由(1)知∠OCD=90°.
∵∠A=∠ACO,∴∠B=∠ACD. 6分
(3)∵∠EAO=∠BAC,∠AOE=∠ACB=90°,
∴△AOE∽△ACB,∴∠B=∠AEO. 7分
∵∠B=∠ACD,∠AEO=∠DEC,
∴∠DCE=∠DEC,
∴DE=CD=3.
又∵OD=5,∴OE=2,OC=4,∴AE==2. 8分
由△AOE∽△ACB得=,
∴=,∴BC=. 10分
26.解:(1)3. 2分
提示:如图1,连接AO,BO,过点O作OH⊥AB于点H.
∵OA=OB=6,AB=6,OH⊥BA,
∴AH=3,
∴OH===3,
∴点O到AB的距离是3.
(2)∵S△ABC=×AB×h(点C到AB的距离),且AB的长是定值,
∴当点C到AB的距离最大时,△ABC的面积有最大值. 4分
如图2,过点O作OE⊥AB于点E,当E,O,C'三点共线时,点C'到AB的距离最大,
∴AE=BE=8.
∵☉O的半径为10.
∴OE===6. 6分
当E,O,C'三点共线,即EC'=10+6=16时,△ABC的面积最大,
∴△ABC的面积最大值=×16×16=128. 7分
(3)①如图3,连接AO,DO.
∵△ABP是等腰直角三角形,
∴∠ABP=∠BAP=45°,∠APB=∠CPD=90°,
∴∠AOD=2∠ABD=90°,∠ACD=∠ABP=45°,∠BDC=∠CAB=45°,
∴△AOD是等腰直角三角形,△DPC是等腰直角三角形. 9分
∵☉O的直径为60 m,
∴AO=DO=30 m.
∵AD2=AO2+DO2=DP2+AP2=1800,S△ABP=AP2,S△CDP=DP2,
∴S△ABP+S△CDP=(AP2+DP2)=900(m2),
∴S1=900 m2. 10分
②∵S△ADP=×AP×DP,S△BCP=×CP×BP,∴S2=S△ADP+S△BCP=AP×DP.
∵(AP-DP)2≥0,
∴AP2+DP2≥2AP×DP.
∵DP2+AP2=1800,
∴S2=AP×DP≤900,
∴S2的最大值为900 m2. 12分
同课章节目录
