第11章三角形:用转化思想求不规则图形的角度素养训练课件 16张PPT 2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 第11章三角形:用转化思想求不规则图形的角度素养训练课件 16张PPT 2023-2024学年人教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 185.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 21:08:25 | ||
图片预览




文档简介
(共16张PPT)
第十一章 三角形
用转化思想求不规则图形的角度
训练
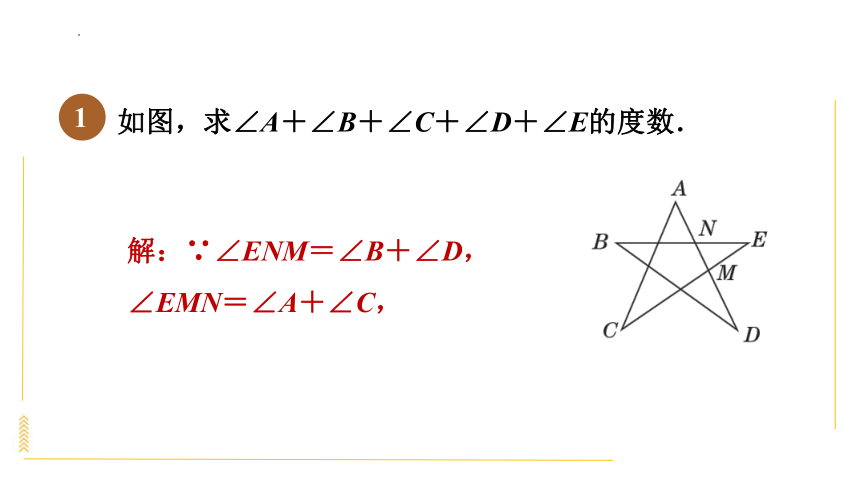
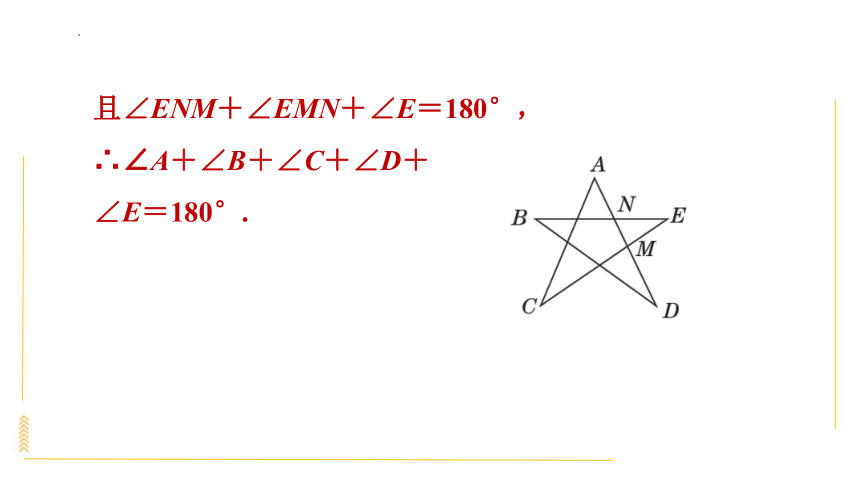
如图,求∠A+∠B+∠C+∠D+∠E的度数.
1
解:∵∠ENM=∠B+∠D,
∠EMN=∠A+∠C,
且∠ENM+∠EMN+∠E=180°,
∴∠A+∠B+∠C+∠D+
∠E=180°.
如图,求∠A+∠ABC+∠C+∠D+∠E+∠F的度数.
2
解:∵∠BGF=∠A+∠ABC,
∠GBE=∠C+∠D,
且在四边形BGFE中,∠GBE+
∠BGF+∠F+∠E=360°,
∴∠A+∠ABC+∠C+∠D+
∠E+∠F=360°.
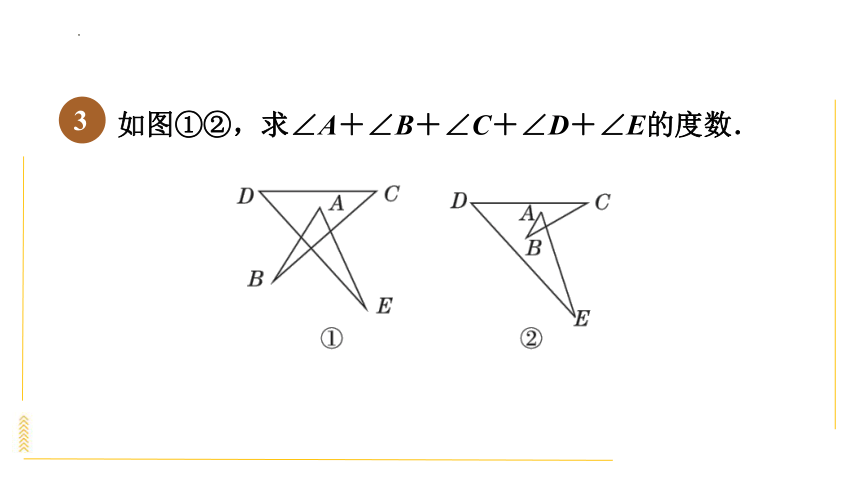
如图①②,求∠A+∠B+∠C+∠D+∠E的度数.
3
解:如图①,根据三角形外角的性质,
可得∠1=∠A+∠B,∠2=∠C+∠D.
∵∠1+∠2+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
如图②,延长EA交CD于点F,设EA与BC交于点G.
根据三角形外角的性质,
可得∠1=∠D+∠E,
∠2=∠BAG+∠B.
∵∠1+∠2+∠C=180°,
∴∠BAG+∠B+∠C+∠D+∠E=180°.
如图,求∠A+∠B+∠C+∠D+∠E的度数.
4
解:如图,连接BC.
在△DEF和△BCF中,
∵∠DFE=∠BFC,
∴∠D+∠E=∠FBC+∠FCB.
在△ABC中,∠A+∠ABE+∠FBC+
∠FCB+∠ACD=180°,
∴∠A+∠ABE+∠ACD+∠D+∠E=180°.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
5
解:如图,连接AB.
∵∠3=∠4,
∴∠1+∠2=∠C+∠F.
∴∠EAC+∠DBF+∠C+∠D+∠E+∠F=∠EAC+∠DBF+∠D+∠E+∠1+∠2=∠EAB+∠ABD+∠D+∠E=360°.
如图,BE,CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
(1)图中共有________个“8字形”;
6
6
(2)若∠B∶∠D∶∠F=4∶6∶x,求x的值.
∵EF平分∠BED,CF平分∠BCD,
∴∠DEG=∠AEG,∠ACH=∠BCH.
∵在△DGE和△FGC中,∠DGE=∠FGC,
∴∠D+∠DEG=∠F+∠ACH.
∵在△BHC和△FHE中,∠BHC=∠FHE,
∴∠B+∠BCH=∠F+∠AEG.
∴∠D+∠DEG+∠B+∠BCH=
∠F+∠ACH+∠F+∠AEG.
∴∠D+∠B=2∠F.
∵∠B∶∠D∶∠F=4∶6∶x,
∴10=2x,则x=5.
第十一章 三角形
用转化思想求不规则图形的角度
训练
如图,求∠A+∠B+∠C+∠D+∠E的度数.
1
解:∵∠ENM=∠B+∠D,
∠EMN=∠A+∠C,
且∠ENM+∠EMN+∠E=180°,
∴∠A+∠B+∠C+∠D+
∠E=180°.
如图,求∠A+∠ABC+∠C+∠D+∠E+∠F的度数.
2
解:∵∠BGF=∠A+∠ABC,
∠GBE=∠C+∠D,
且在四边形BGFE中,∠GBE+
∠BGF+∠F+∠E=360°,
∴∠A+∠ABC+∠C+∠D+
∠E+∠F=360°.
如图①②,求∠A+∠B+∠C+∠D+∠E的度数.
3
解:如图①,根据三角形外角的性质,
可得∠1=∠A+∠B,∠2=∠C+∠D.
∵∠1+∠2+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
如图②,延长EA交CD于点F,设EA与BC交于点G.
根据三角形外角的性质,
可得∠1=∠D+∠E,
∠2=∠BAG+∠B.
∵∠1+∠2+∠C=180°,
∴∠BAG+∠B+∠C+∠D+∠E=180°.
如图,求∠A+∠B+∠C+∠D+∠E的度数.
4
解:如图,连接BC.
在△DEF和△BCF中,
∵∠DFE=∠BFC,
∴∠D+∠E=∠FBC+∠FCB.
在△ABC中,∠A+∠ABE+∠FBC+
∠FCB+∠ACD=180°,
∴∠A+∠ABE+∠ACD+∠D+∠E=180°.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
5
解:如图,连接AB.
∵∠3=∠4,
∴∠1+∠2=∠C+∠F.
∴∠EAC+∠DBF+∠C+∠D+∠E+∠F=∠EAC+∠DBF+∠D+∠E+∠1+∠2=∠EAB+∠ABD+∠D+∠E=360°.
如图,BE,CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
(1)图中共有________个“8字形”;
6
6
(2)若∠B∶∠D∶∠F=4∶6∶x,求x的值.
∵EF平分∠BED,CF平分∠BCD,
∴∠DEG=∠AEG,∠ACH=∠BCH.
∵在△DGE和△FGC中,∠DGE=∠FGC,
∴∠D+∠DEG=∠F+∠ACH.
∵在△BHC和△FHE中,∠BHC=∠FHE,
∴∠B+∠BCH=∠F+∠AEG.
∴∠D+∠DEG+∠B+∠BCH=
∠F+∠ACH+∠F+∠AEG.
∴∠D+∠B=2∠F.
∵∠B∶∠D∶∠F=4∶6∶x,
∴10=2x,则x=5.
