2024年吉林省长春市重点学校中考数学模拟预测试题(无答案)
文档属性
| 名称 | 2024年吉林省长春市重点学校中考数学模拟预测试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 792.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 10:00:57 | ||
图片预览

文档简介
数学学科试卷
一、选择题(每题3分,共24分)
1.计算的值等于( )
A. B. C. D.
2.若关于x的一元二次方程有两个相等的实数根,则实数m的值为( )
A. B.16 C. D.4
3.若,则的值为( )
A. B. C. D.
4.如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取,的中点C,D,量得,则A,B之间的距离是( )
A. B. C. D.
5.凸透镜成像的原理如图所示,.若物体H到焦点F的距离与焦点F到凸透镜中心线的距离之比为,则物体被缩小到原来的( )
A. B. C. D.
6.一个住宅区的配电房示意图如图所示,它是一个轴对称图形,则配电房房顶离地面的高度为( )
A. B. C. D.
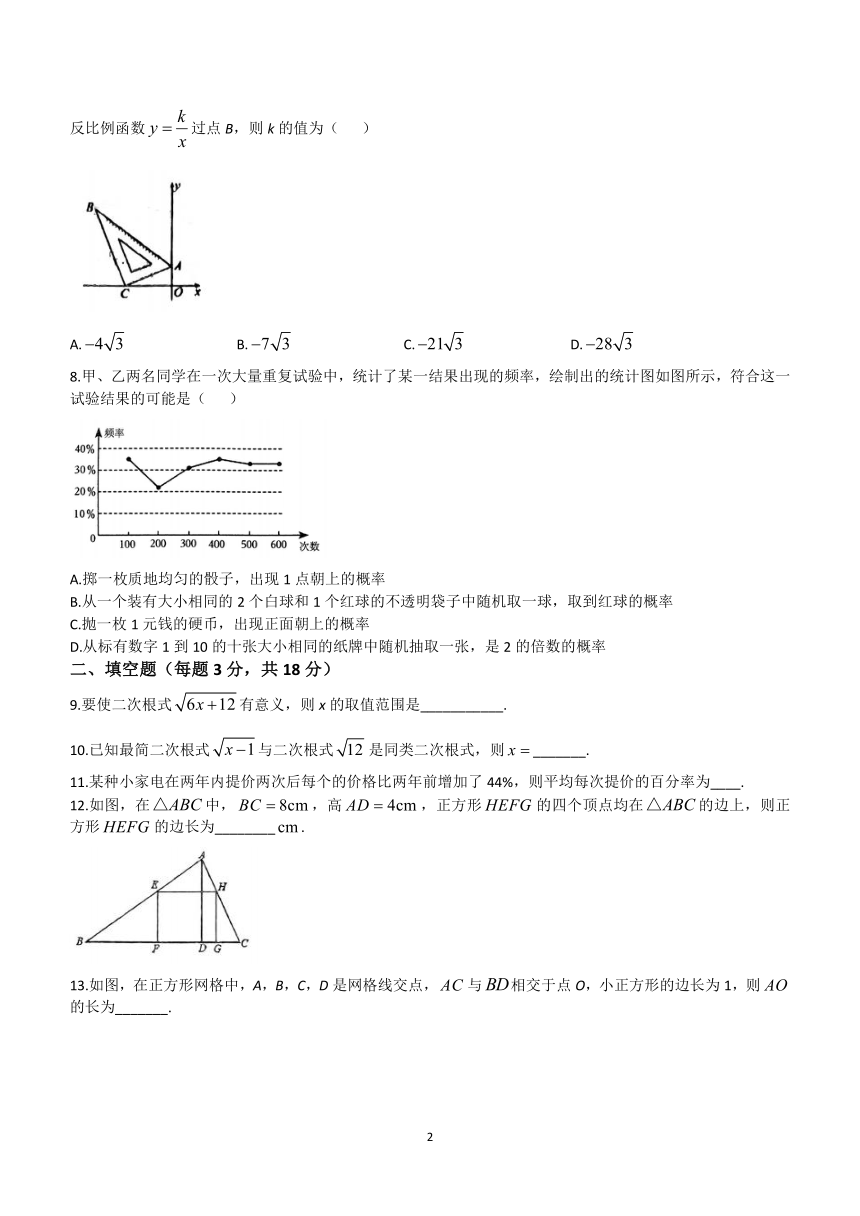
7.一块直角三角尺按如图放置,顶点A的坐标为,直角顶点C的坐标为,,反比例函数过点B,则k的值为( )
A. B. C. D.
8.甲、乙两名同学在一次大量重复试验中,统计了某一结果出现的频率,绘制出的统计图如图所示,符合这一试验结果的可能是( )
A.掷一枚质地均匀的骰子,出现1点朝上的概率
B.从一个装有大小相同的2个白球和1个红球的不透明袋子中随机取一球,取到红球的概率
C.抛一枚1元钱的硬币,出现正面朝上的概率
D.从标有数字1到10的十张大小相同的纸牌中随机抽取一张,是2的倍数的概率
二、填空题(每题3分,共18分)
9.要使二次根式有意义,则x的取值范围是___________.
10.已知最简二次根式与二次根式是同类二次根式,则_______.
11.某种小家电在两年内提价两次后每个的价格比两年前增加了44%,则平均每次提价的百分率为____.
12.如图,在中,,高,正方形的四个顶点均在的边上,则正方形的边长为________.
13.如图,在正方形网格中,A,B,C,D是网格线交点,与相交于点O,小正方形的边长为1,则的长为_______.
14.如图,菱形的对角线、相交于点O,过点D作于点H,连接,若,,则菱形的面积为是____.
三、解答题(共78分)
15.(6分)计算:.
16.(6分)老师让同学们解方程,小红同学给出了如下的解答过程:
解方程:.解:,……第一步……第二步,……第三步
(1)小红同学是用___________(选“配方法”、“公式法”或“因式分解法”)方法求解的,从第__________步开始出现错误.
(2)请你用适当的方法解该方程.
17.(6分)如图,两个相同的可以自由转动的转盘A和B,转盘A被三等分,分别标有数字6,2,1;转盘B被四等分,分别标有数字,,,.(当指针指在两个扇形的交线时,需重新转动转盘)
A B
(1)转动转盘B一次,转盘停止时,指针指向偶数的概率为________________;
(2)同时转动两个转盘,转盘停止时,求两个指针指向的数字之和大于0的概率.(画树状图或列表法)
18.(7分)证明:对于任何实数m,关于x的方程总有两个不相等的实数根.
19.(7分)如图,在中,,.
(1)求证:.
(2)如果和的面积分别为4和9,则四边形的面积为__________.
20.(7分)在一次数学综合实践活动中,小明计划测量城门大楼的高度.如图,在点B处测得楼顶A的仰角为,他正对城楼前进31米到达C处,再登上2米高的楼台D处,并测得此时楼顶A的仰角为.求城门大楼的高度;(结果保留整数)(参考数据:,,)
21.(8分)如图是由边长为1的小正方形组成的网格,每个小正方形的顶点叫做格点.正方形四个顶点都是格点,F是上的格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
图(1) 图(2)
(1)在图(1)中,先将线段绕点D顺时针旋转,画对应线段,再在上画点M,并连接,使;
(2)在图(2)中,G是与网格线的交点,先画点G关于的对称点H,连接,则的面积为____________.
22.(9分)先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式.
解:,
可化为.
由有理数的乘法法则“两数相乘,同号得正”,得
①,②,
解不等式组①,得,解不等式组②,得,
的解集为或,
即一元二次不等式的解集为或.
(1)一元二次不等式的解集为______________;
(2)分式不等式的解集为_______________;
(3)解一元二次不等式.
23.(10分)在中,,D是边的中点,以D为角的顶点作.如图1,射线经过点A,交边于点E.
图1 图2 图3
(1)不添加辅助线,请直接写出图1中所有与相似的三角形;
(2)如图2,将从图1中的位置开始,绕点D按逆时针方向旋转(旋转角不大于α),射线,分别交,于点E,F.
①求证:;
②如图3,若,,在线段上有一点P,且,若点P始终在内(包括边界上),求的取值范围;
③若,直接写出旋转角为多少度时,与相似.
24.(12分)如图1,平面上,四边形中,,,,,,点M在边上,且.点P沿折线以1个单位速度向终点C运动,点是点A关于直线的对称点,连接,设点P在该折线上运动的时间为.
图1 图2
(1)直接写出线段的长;
(2)如图2,连接.
①求的度数,并直接写出当、M、A共线时t的值;
②若点P到的距离为1,求的值;
(3)当时,请直接写出点到直线的距离(用含t的式子表示).
一、选择题(每题3分,共24分)
1.计算的值等于( )
A. B. C. D.
2.若关于x的一元二次方程有两个相等的实数根,则实数m的值为( )
A. B.16 C. D.4
3.若,则的值为( )
A. B. C. D.
4.如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取,的中点C,D,量得,则A,B之间的距离是( )
A. B. C. D.
5.凸透镜成像的原理如图所示,.若物体H到焦点F的距离与焦点F到凸透镜中心线的距离之比为,则物体被缩小到原来的( )
A. B. C. D.
6.一个住宅区的配电房示意图如图所示,它是一个轴对称图形,则配电房房顶离地面的高度为( )
A. B. C. D.
7.一块直角三角尺按如图放置,顶点A的坐标为,直角顶点C的坐标为,,反比例函数过点B,则k的值为( )
A. B. C. D.
8.甲、乙两名同学在一次大量重复试验中,统计了某一结果出现的频率,绘制出的统计图如图所示,符合这一试验结果的可能是( )
A.掷一枚质地均匀的骰子,出现1点朝上的概率
B.从一个装有大小相同的2个白球和1个红球的不透明袋子中随机取一球,取到红球的概率
C.抛一枚1元钱的硬币,出现正面朝上的概率
D.从标有数字1到10的十张大小相同的纸牌中随机抽取一张,是2的倍数的概率
二、填空题(每题3分,共18分)
9.要使二次根式有意义,则x的取值范围是___________.
10.已知最简二次根式与二次根式是同类二次根式,则_______.
11.某种小家电在两年内提价两次后每个的价格比两年前增加了44%,则平均每次提价的百分率为____.
12.如图,在中,,高,正方形的四个顶点均在的边上,则正方形的边长为________.
13.如图,在正方形网格中,A,B,C,D是网格线交点,与相交于点O,小正方形的边长为1,则的长为_______.
14.如图,菱形的对角线、相交于点O,过点D作于点H,连接,若,,则菱形的面积为是____.
三、解答题(共78分)
15.(6分)计算:.
16.(6分)老师让同学们解方程,小红同学给出了如下的解答过程:
解方程:.解:,……第一步……第二步,……第三步
(1)小红同学是用___________(选“配方法”、“公式法”或“因式分解法”)方法求解的,从第__________步开始出现错误.
(2)请你用适当的方法解该方程.
17.(6分)如图,两个相同的可以自由转动的转盘A和B,转盘A被三等分,分别标有数字6,2,1;转盘B被四等分,分别标有数字,,,.(当指针指在两个扇形的交线时,需重新转动转盘)
A B
(1)转动转盘B一次,转盘停止时,指针指向偶数的概率为________________;
(2)同时转动两个转盘,转盘停止时,求两个指针指向的数字之和大于0的概率.(画树状图或列表法)
18.(7分)证明:对于任何实数m,关于x的方程总有两个不相等的实数根.
19.(7分)如图,在中,,.
(1)求证:.
(2)如果和的面积分别为4和9,则四边形的面积为__________.
20.(7分)在一次数学综合实践活动中,小明计划测量城门大楼的高度.如图,在点B处测得楼顶A的仰角为,他正对城楼前进31米到达C处,再登上2米高的楼台D处,并测得此时楼顶A的仰角为.求城门大楼的高度;(结果保留整数)(参考数据:,,)
21.(8分)如图是由边长为1的小正方形组成的网格,每个小正方形的顶点叫做格点.正方形四个顶点都是格点,F是上的格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
图(1) 图(2)
(1)在图(1)中,先将线段绕点D顺时针旋转,画对应线段,再在上画点M,并连接,使;
(2)在图(2)中,G是与网格线的交点,先画点G关于的对称点H,连接,则的面积为____________.
22.(9分)先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式.
解:,
可化为.
由有理数的乘法法则“两数相乘,同号得正”,得
①,②,
解不等式组①,得,解不等式组②,得,
的解集为或,
即一元二次不等式的解集为或.
(1)一元二次不等式的解集为______________;
(2)分式不等式的解集为_______________;
(3)解一元二次不等式.
23.(10分)在中,,D是边的中点,以D为角的顶点作.如图1,射线经过点A,交边于点E.
图1 图2 图3
(1)不添加辅助线,请直接写出图1中所有与相似的三角形;
(2)如图2,将从图1中的位置开始,绕点D按逆时针方向旋转(旋转角不大于α),射线,分别交,于点E,F.
①求证:;
②如图3,若,,在线段上有一点P,且,若点P始终在内(包括边界上),求的取值范围;
③若,直接写出旋转角为多少度时,与相似.
24.(12分)如图1,平面上,四边形中,,,,,,点M在边上,且.点P沿折线以1个单位速度向终点C运动,点是点A关于直线的对称点,连接,设点P在该折线上运动的时间为.
图1 图2
(1)直接写出线段的长;
(2)如图2,连接.
①求的度数,并直接写出当、M、A共线时t的值;
②若点P到的距离为1,求的值;
(3)当时,请直接写出点到直线的距离(用含t的式子表示).
同课章节目录
