2024年中考数学高频压轴题训练——二次函数与最值(含答案)
文档属性
| 名称 | 2024年中考数学高频压轴题训练——二次函数与最值(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 745.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 23:08:57 | ||
图片预览

文档简介
2024年中考数学高频压轴题训练——二次函数与最值
1.在平面直角坐标系中,已知抛物线y=ax2+bx﹣4经过A(﹣4,0),C(2,0)两点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
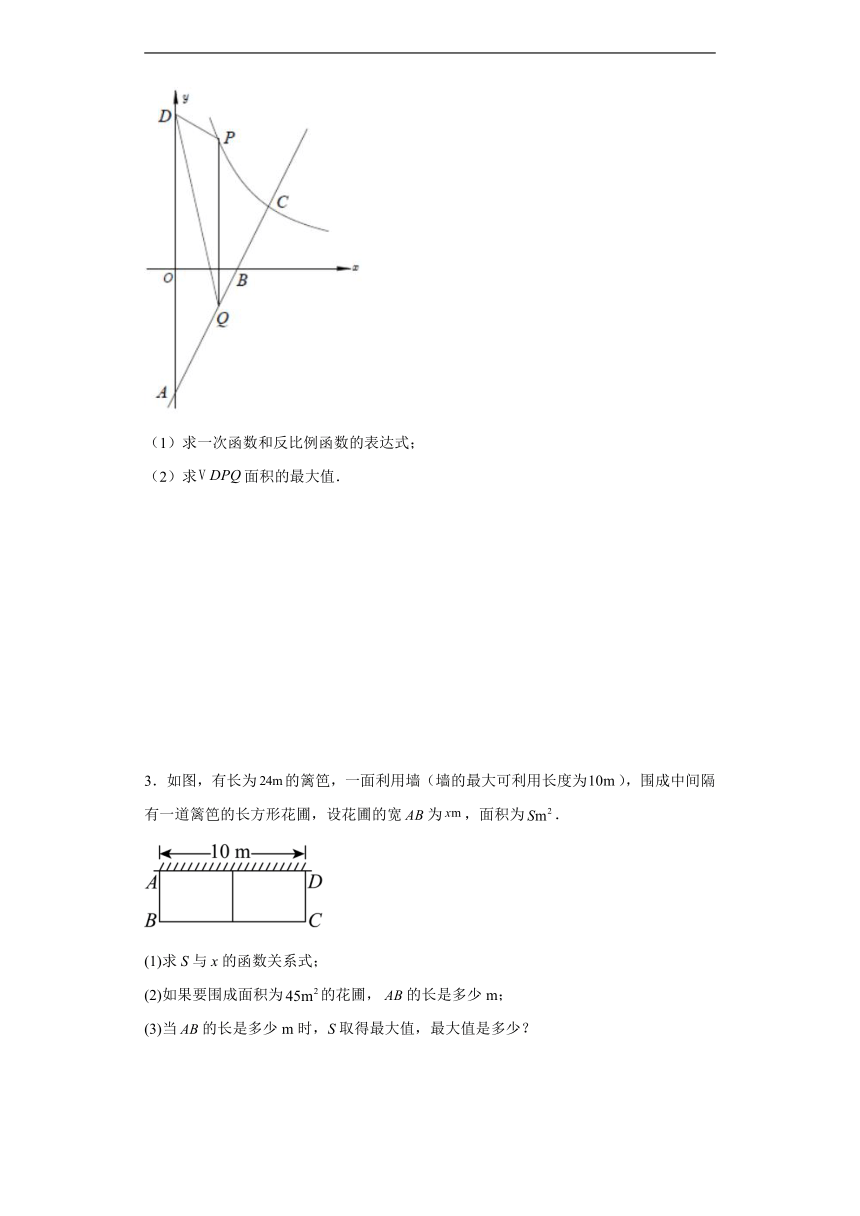
2.如图在平面直角坐标系中,一次函数的图像经过点、交反比例函数的图像于点,点在反比例函数的图像上,横坐标为,轴交直线于点,是轴上任意一点,连接、.
(1)求一次函数和反比例函数的表达式;
(2)求面积的最大值.
3.如图,有长为的篱笆,一面利用墙(墙的最大可利用长度为),围成中间隔有一道篱笆的长方形花圃,设花圃的宽为,面积为.
(1)求S与x的函数关系式;
(2)如果要围成面积为的花圃,的长是多少m;
(3)当的长是多少m时,S取得最大值,最大值是多少?
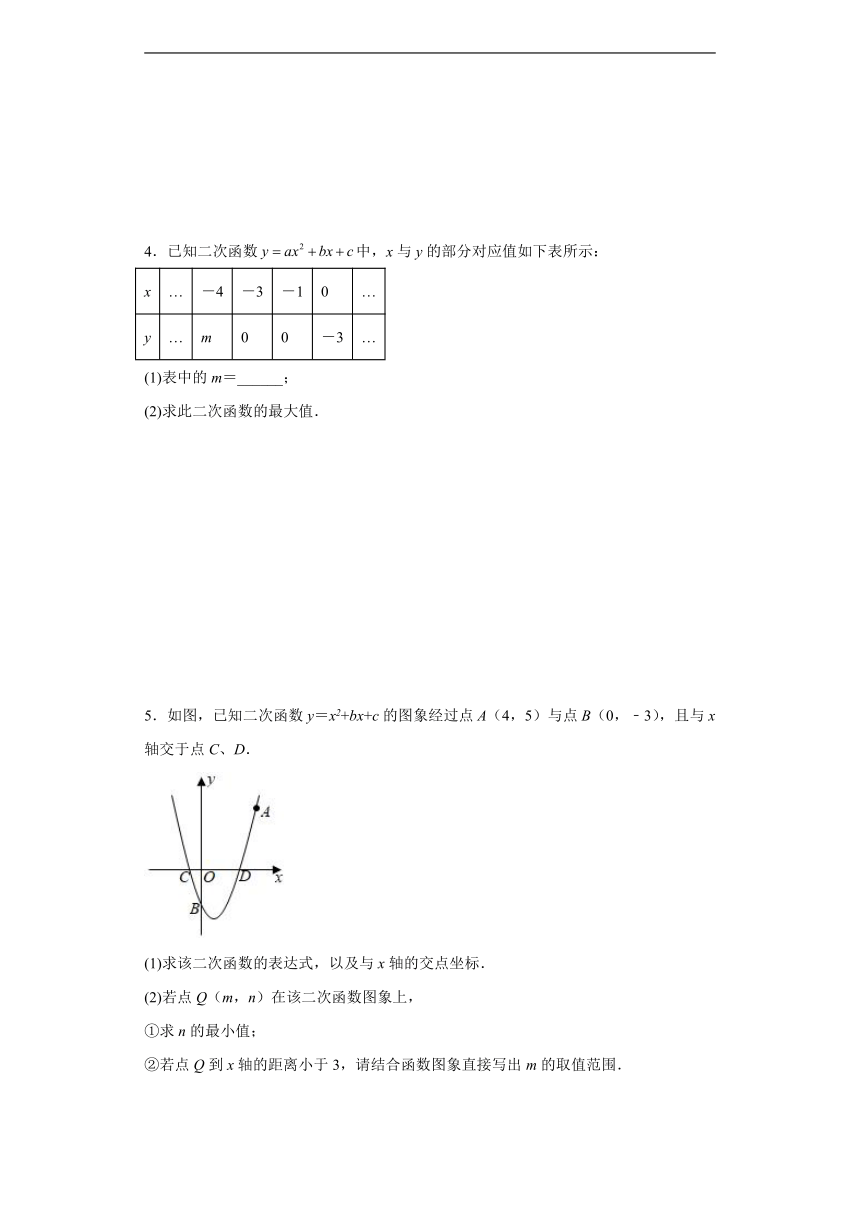
4.已知二次函数中,x与y的部分对应值如下表所示:
x … -4 -3 -1 0 …
y … m 0 0 -3 …
(1)表中的m=______;
(2)求此二次函数的最大值.
5.如图,已知二次函数y=x2+bx+c的图象经过点A(4,5)与点B(0,﹣3),且与x轴交于点C、D.
(1)求该二次函数的表达式,以及与x轴的交点坐标.
(2)若点Q(m,n)在该二次函数图象上,
①求n的最小值;
②若点Q到x轴的距离小于3,请结合函数图象直接写出m的取值范围.
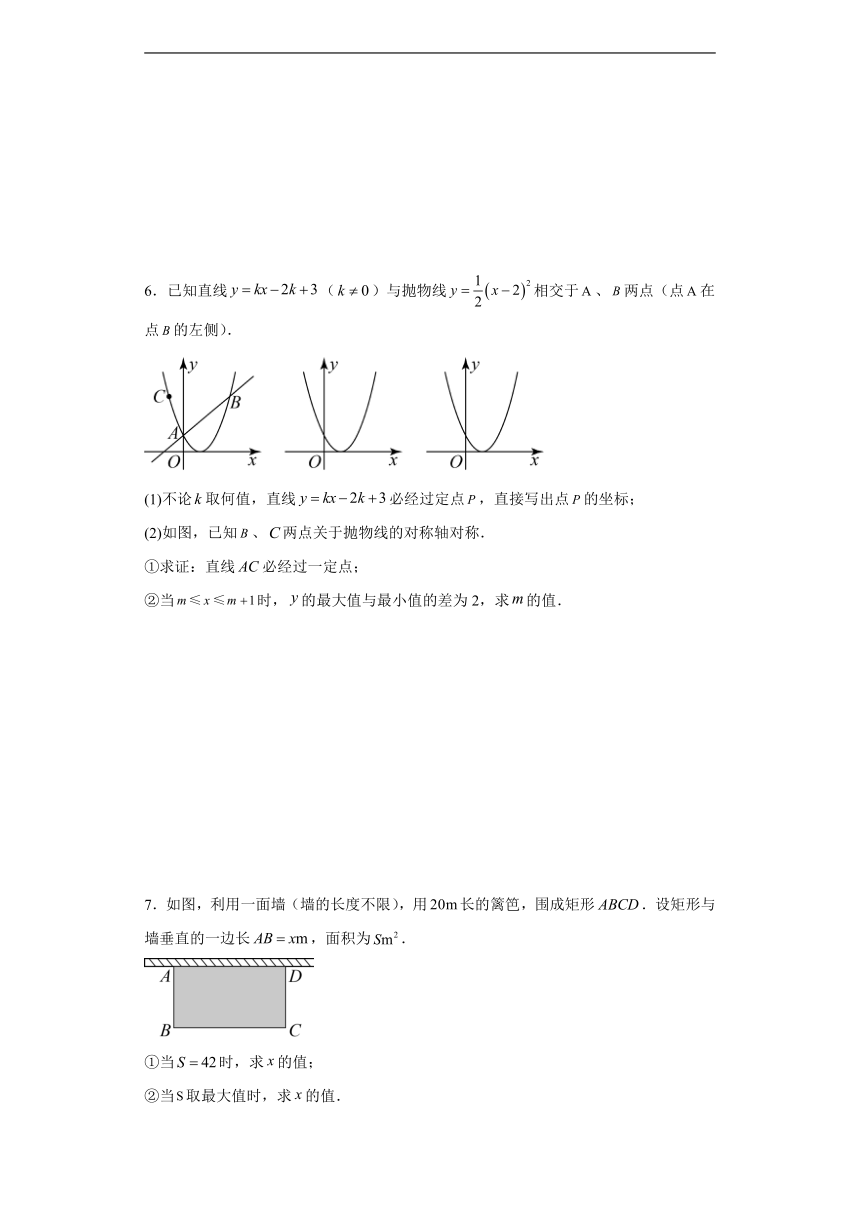
6.已知直线()与抛物线相交于、两点(点在点的左侧).
(1)不论取何值,直线必经过定点,直接写出点的坐标;
(2)如图,已知、两点关于抛物线的对称轴对称.
①求证:直线必经过一定点;
②当时,的最大值与最小值的差为2,求的值.
7.如图,利用一面墙(墙的长度不限),用长的篱笆,围成矩形.设矩形与墙垂直的一边长,面积为.
①当时,求的值;
②当取最大值时,求的值.
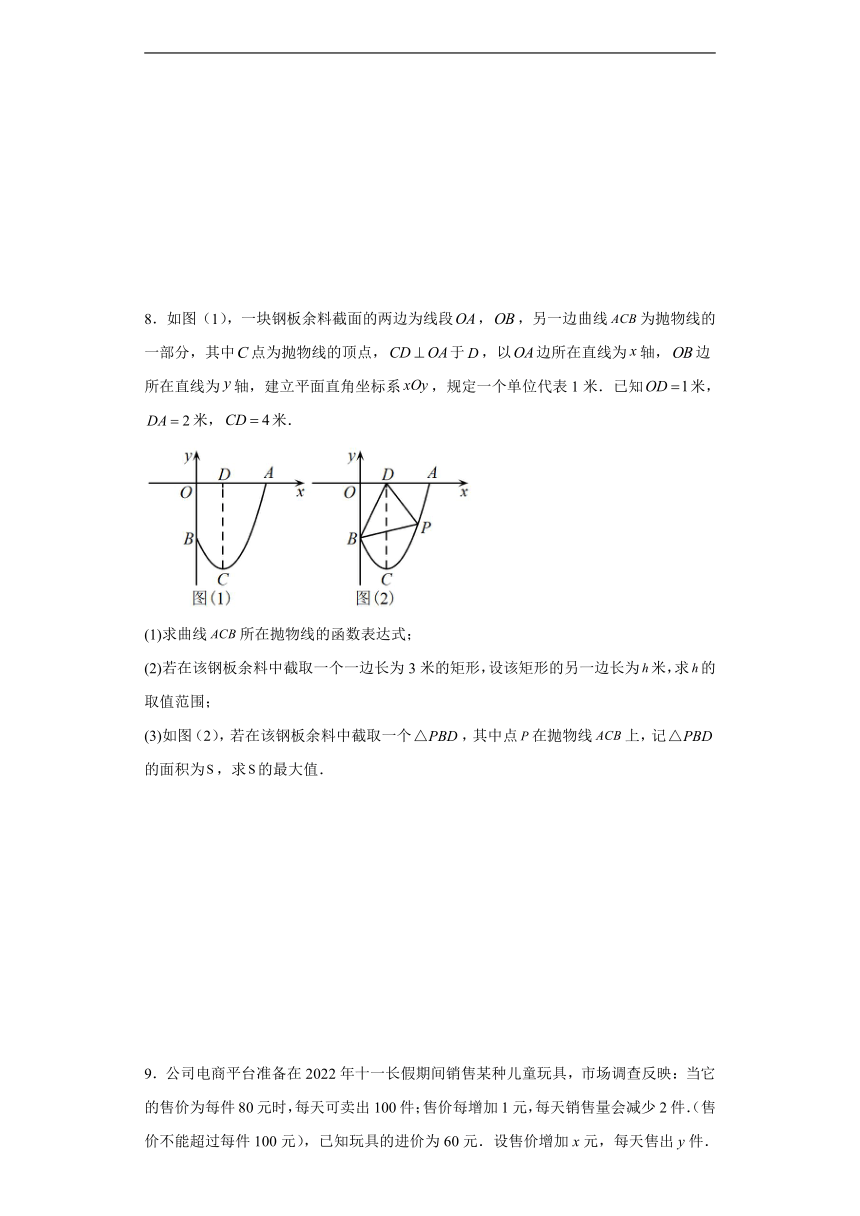
8.如图(1),一块钢板余料截面的两边为线段,,另一边曲线为抛物线的一部分,其中点为抛物线的顶点,于,以边所在直线为轴,边所在直线为轴,建立平面直角坐标系,规定一个单位代表1米.已知米,米,米.
(1)求曲线所在抛物线的函数表达式;
(2)若在该钢板余料中截取一个一边长为3米的矩形,设该矩形的另一边长为米,求的取值范围;
(3)如图(2),若在该钢板余料中截取一个,其中点在抛物线上,记的面积为,求的最大值.
9.公司电商平台准备在2022年十一长假期间销售某种儿童玩具,市场调查反映:当它的售价为每件80元时,每天可卖出100件;售价每增加1元,每天销售量会减少2件.(售价不能超过每件100元),已知玩具的进价为60元.设售价增加x元,每天售出y件.
(1)请直接写出y与x之间的函数表达式;
(2)求当x为多少时,平台每天销售这种玩具可获利润2250元?
(3)设平台每天销售这种玩具可获利w元,求当x为多少时,w最大,最大值是多少?
10.如图,已知二次函数的图像经过点.
(1)求该二次函数的表达式;
(2)当x取何值时,该二次函数取得最大值?最大值是多少?
(3)当时,请写出x的取值范围.
11.如图,直线与反比例函数的图象交于点,与轴交于点,平行于轴的直线交反比例函数的图象于点,交于点,连接.
(1)求的值和反比例函数的表达式;
(2)观察图象,直接写出当时,不等式的解集;
(3)直线沿轴方向平移,当为何值时,的面积最大?最大值是多少?
12.如图,在平面直角坐标系中,过点、两点的抛物线的顶点C在x轴正半轴上.
(1)求抛物线的解析式;
(2)求点C的坐标;
(3)为线段AB上一点,,作轴交抛物线于点M,求PM的最大值?
13.已知:如图,二次函数与x轴交于点和点.
(1)求抛物线的解析式.
(2)当时,求二次函数的最大值和最小值.
(3)点P是抛物线上一点,其横坐标为m,过点P作轴,点Q的纵坐标为,已知点P与点Q不重合,且线段的长度随m的增大而减小.
①求m的取值范围.
②当时,在线段的右边作正方形,直接写出正方形与二次函数的图象交点的个数及对应的m的取值范围.
14.如图1,抛物线与x轴交于点x和点,与y轴交于点C,且,P为上方抛物线上一动点,其横坐标为m.
(1)求抛物线的解析式;
(2)若,求点P的坐标;
(3)如图2,过点P作,求的最大值.
15.已知抛物线与x轴交于A、B两点,顶点为C,连接,点P在线段下方的抛物线上运动.
(1)如图1,连接,,若,求点P的坐标.
(2)如图2,过点P作轴交于点Q,交于点H,求周长的最大值.
(3)如图3,直线,分别与y轴交于点E,F,当点P运动时,是否为定值?若是,试求出该定值;若不是,请说明理由.
试卷第1页,共3页
参考答案:
1.(1) ;(2)S关于m的函数关系式为 , S的最大值为4.
2.(1);(2)
3.(1)
(2)当为时,面积为
(3)当的长是米时,围成的花圃的面积最大,最大面积是平方米
4.(1)-3
(2)1
5.(1),与x轴的交点坐标为和
(2)①-4;②1﹣<m<0或2<m<1+
6.(1)
(2)②或
7.①或;②
8.(1)
(2)
(3)
9.(1)
(2)5元
(3)当x为15元时w最大,最大值是2450元
10.(1)
(2),最大值为4
(3)
11.(1),
(2);
(3)时,的面积最大,最大值为.
12.(1)
(2)
(3)
13.(1)
(2)有最大值5,最小值
(3)①或;②当时,正方形与抛物线有一个交点;当,时,正方形与抛物线有两个交点;当时,正方形与抛物线有三个交点
14.(1)抛物线的解析式
(2)点的坐标为或
(3)的最大值为
15.(1)或;
(2)最大值为;
(3)当点P运动时,为定值,定值为8.
答案第1页,共2页
1.在平面直角坐标系中,已知抛物线y=ax2+bx﹣4经过A(﹣4,0),C(2,0)两点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
2.如图在平面直角坐标系中,一次函数的图像经过点、交反比例函数的图像于点,点在反比例函数的图像上,横坐标为,轴交直线于点,是轴上任意一点,连接、.
(1)求一次函数和反比例函数的表达式;
(2)求面积的最大值.
3.如图,有长为的篱笆,一面利用墙(墙的最大可利用长度为),围成中间隔有一道篱笆的长方形花圃,设花圃的宽为,面积为.
(1)求S与x的函数关系式;
(2)如果要围成面积为的花圃,的长是多少m;
(3)当的长是多少m时,S取得最大值,最大值是多少?
4.已知二次函数中,x与y的部分对应值如下表所示:
x … -4 -3 -1 0 …
y … m 0 0 -3 …
(1)表中的m=______;
(2)求此二次函数的最大值.
5.如图,已知二次函数y=x2+bx+c的图象经过点A(4,5)与点B(0,﹣3),且与x轴交于点C、D.
(1)求该二次函数的表达式,以及与x轴的交点坐标.
(2)若点Q(m,n)在该二次函数图象上,
①求n的最小值;
②若点Q到x轴的距离小于3,请结合函数图象直接写出m的取值范围.
6.已知直线()与抛物线相交于、两点(点在点的左侧).
(1)不论取何值,直线必经过定点,直接写出点的坐标;
(2)如图,已知、两点关于抛物线的对称轴对称.
①求证:直线必经过一定点;
②当时,的最大值与最小值的差为2,求的值.
7.如图,利用一面墙(墙的长度不限),用长的篱笆,围成矩形.设矩形与墙垂直的一边长,面积为.
①当时,求的值;
②当取最大值时,求的值.
8.如图(1),一块钢板余料截面的两边为线段,,另一边曲线为抛物线的一部分,其中点为抛物线的顶点,于,以边所在直线为轴,边所在直线为轴,建立平面直角坐标系,规定一个单位代表1米.已知米,米,米.
(1)求曲线所在抛物线的函数表达式;
(2)若在该钢板余料中截取一个一边长为3米的矩形,设该矩形的另一边长为米,求的取值范围;
(3)如图(2),若在该钢板余料中截取一个,其中点在抛物线上,记的面积为,求的最大值.
9.公司电商平台准备在2022年十一长假期间销售某种儿童玩具,市场调查反映:当它的售价为每件80元时,每天可卖出100件;售价每增加1元,每天销售量会减少2件.(售价不能超过每件100元),已知玩具的进价为60元.设售价增加x元,每天售出y件.
(1)请直接写出y与x之间的函数表达式;
(2)求当x为多少时,平台每天销售这种玩具可获利润2250元?
(3)设平台每天销售这种玩具可获利w元,求当x为多少时,w最大,最大值是多少?
10.如图,已知二次函数的图像经过点.
(1)求该二次函数的表达式;
(2)当x取何值时,该二次函数取得最大值?最大值是多少?
(3)当时,请写出x的取值范围.
11.如图,直线与反比例函数的图象交于点,与轴交于点,平行于轴的直线交反比例函数的图象于点,交于点,连接.
(1)求的值和反比例函数的表达式;
(2)观察图象,直接写出当时,不等式的解集;
(3)直线沿轴方向平移,当为何值时,的面积最大?最大值是多少?
12.如图,在平面直角坐标系中,过点、两点的抛物线的顶点C在x轴正半轴上.
(1)求抛物线的解析式;
(2)求点C的坐标;
(3)为线段AB上一点,,作轴交抛物线于点M,求PM的最大值?
13.已知:如图,二次函数与x轴交于点和点.
(1)求抛物线的解析式.
(2)当时,求二次函数的最大值和最小值.
(3)点P是抛物线上一点,其横坐标为m,过点P作轴,点Q的纵坐标为,已知点P与点Q不重合,且线段的长度随m的增大而减小.
①求m的取值范围.
②当时,在线段的右边作正方形,直接写出正方形与二次函数的图象交点的个数及对应的m的取值范围.
14.如图1,抛物线与x轴交于点x和点,与y轴交于点C,且,P为上方抛物线上一动点,其横坐标为m.
(1)求抛物线的解析式;
(2)若,求点P的坐标;
(3)如图2,过点P作,求的最大值.
15.已知抛物线与x轴交于A、B两点,顶点为C,连接,点P在线段下方的抛物线上运动.
(1)如图1,连接,,若,求点P的坐标.
(2)如图2,过点P作轴交于点Q,交于点H,求周长的最大值.
(3)如图3,直线,分别与y轴交于点E,F,当点P运动时,是否为定值?若是,试求出该定值;若不是,请说明理由.
试卷第1页,共3页
参考答案:
1.(1) ;(2)S关于m的函数关系式为 , S的最大值为4.
2.(1);(2)
3.(1)
(2)当为时,面积为
(3)当的长是米时,围成的花圃的面积最大,最大面积是平方米
4.(1)-3
(2)1
5.(1),与x轴的交点坐标为和
(2)①-4;②1﹣<m<0或2<m<1+
6.(1)
(2)②或
7.①或;②
8.(1)
(2)
(3)
9.(1)
(2)5元
(3)当x为15元时w最大,最大值是2450元
10.(1)
(2),最大值为4
(3)
11.(1),
(2);
(3)时,的面积最大,最大值为.
12.(1)
(2)
(3)
13.(1)
(2)有最大值5,最小值
(3)①或;②当时,正方形与抛物线有一个交点;当,时,正方形与抛物线有两个交点;当时,正方形与抛物线有三个交点
14.(1)抛物线的解析式
(2)点的坐标为或
(3)的最大值为
15.(1)或;
(2)最大值为;
(3)当点P运动时,为定值,定值为8.
答案第1页,共2页
同课章节目录
