1.3.2函数的奇偶性

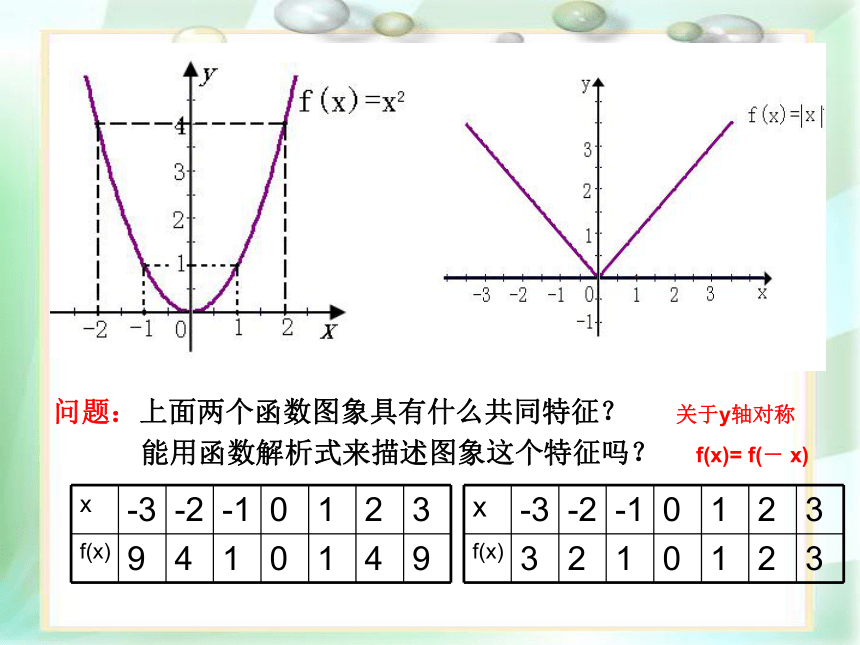
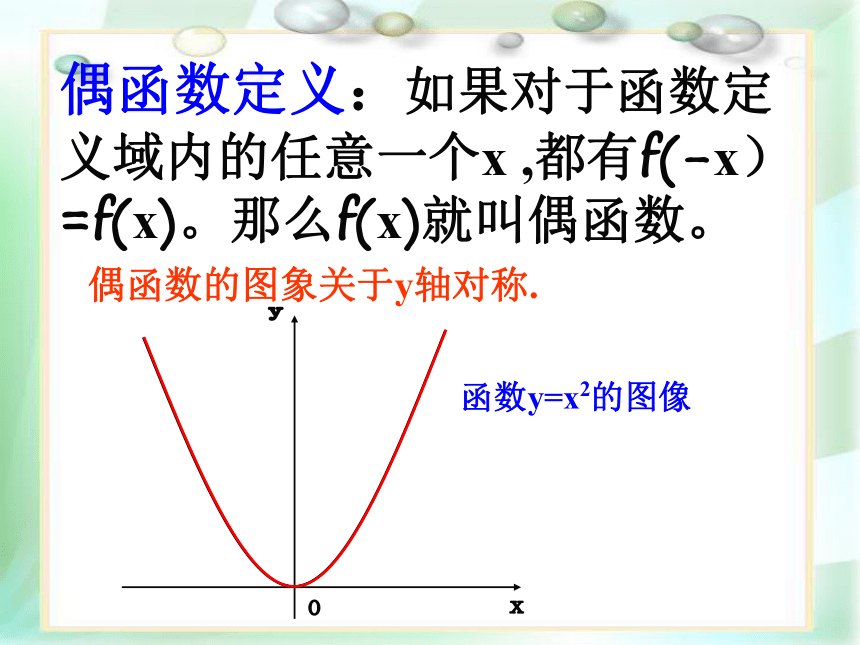
课件13张PPT。函数的奇偶性问题：上面两个函数图象具有什么共同特征？关于y轴对称f(x)= f(－ x)能用函数解析式来描述图象这个特征吗？偶函数定义：如果对于函数定义域内的任意一个x ,都有f(-x）=f(x)。那么f(x)就叫偶函数。偶函数的图象关于y轴对称.函数y=x2的图像观察上面两个图象,你能得出图象的共同特征吗?
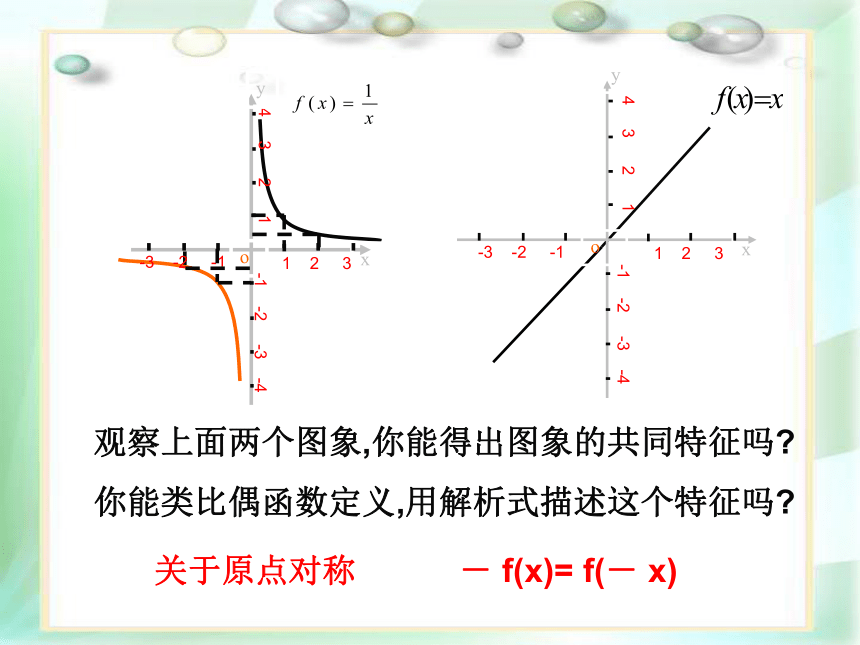
你能类比偶函数定义,用解析式描述这个特征吗?关于原点对称－ f(x)= f(－ x)奇函数定义：如果对于函数定义域内的任意一个x ,都有f(-x) =
-f(x)。那么f(x)就叫奇函数。奇函数的图像特征函数y=x3的图像O
奇函数的图象关于原点对称.
例1.根据下列函数图象,判断函数奇偶性.
yxyxyx-12yx-11判断函数奇偶性步骤:
(1)先确定函数定义域,并判断
定义域是否关于原点对称;
(2)确定f(x)与f(-x)的关系;
(3)作出结论:
若f(-x)=f(x)或f(-x)-f(x)=0,
则f(x)是偶函数;
若f(-x)= - f(x)或f(-x)+f(x)=0,
则f(x)是奇函数.奇偶性定义:对于函数f(x),在它的定义域内，把任意一个x换成-x，(x,-x均在定义域内）
①若有f(-x)=-f(x), 则f(x)叫做奇函数；
②若有f(-x)=f(x), 则f(x)叫做偶函数。
定义域关于原点对称是函数具有奇偶性的前提条件。
性质: 奇函数的图象关于原点对称;
偶函数的图象关于y轴对称.
判断奇偶性方法：图象法，定义法。思考：(1)判断函数 的奇偶性.
(2)如果右图是函数
图象一部分,你能根据f(x)
的奇偶性画出它在y轴
左边的图象吗?yx0f(x)是奇函数.
其图象关于原点对称.