七年级数学下册试题 12.2证明-苏科版(含答案)
文档属性
| 名称 | 七年级数学下册试题 12.2证明-苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 349.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 14:00:46 | ||
图片预览


文档简介
12.2证明
一、选择题.
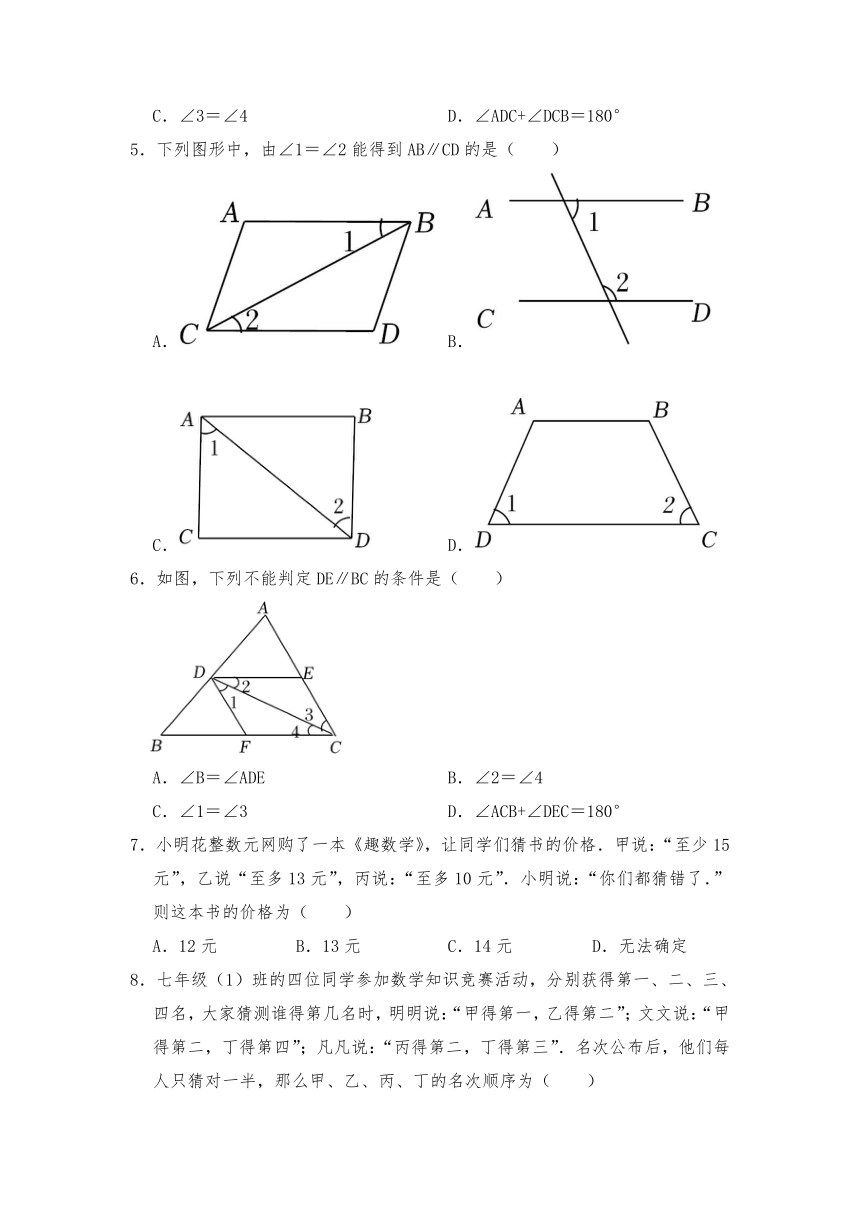
1.如图,下列条件中,不能判定AB∥CD的是( )
A.∠D+∠BAD=180° B.∠1=∠2
C.∠3=∠4 D.∠B=∠DCE
2.如图,①∠1=∠3,②∠2=∠3,③∠1=∠4,④∠2+∠5=180°可以判定b∥c的条件有( )
A.①②④ B.①②③ C.②③④ D.①②③④
3.如图,BD平分∠ABC,若∠1=∠2,则( )
A.AD=BC B.AB=CD C.AB∥CD D.AD∥BC
4.如图,下列条件中,不能判定AD∥BC的是( )
A.∠1=∠2 B.∠BAD+∠ADC=180°
C.∠3=∠4 D.∠ADC+∠DCB=180°
5.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. B.
C. D.
6.如图,下列不能判定DE∥BC的条件是( )
A.∠B=∠ADE B.∠2=∠4
C.∠1=∠3 D.∠ACB+∠DEC=180°
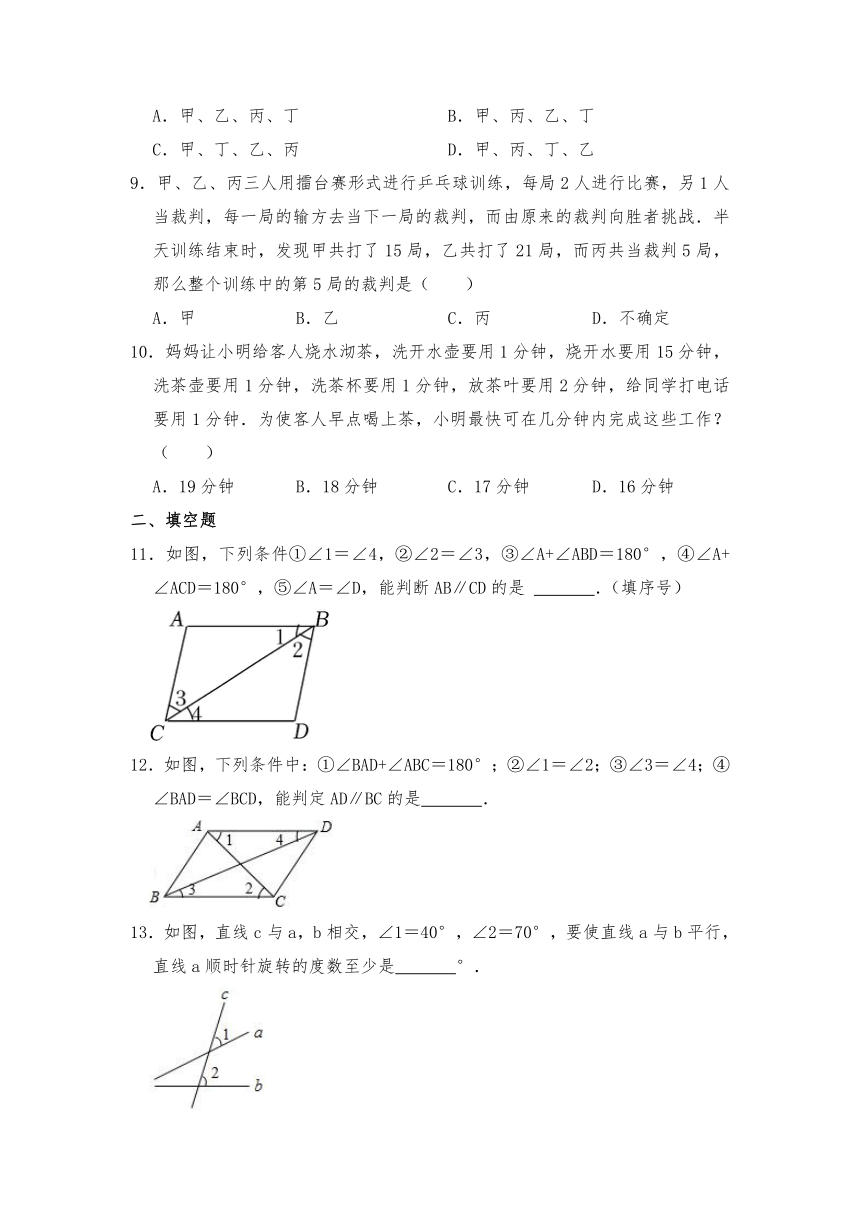
7.小明花整数元网购了一本《趣数学》,让同学们猜书的价格.甲说:“至少15元”,乙说“至多13元”,丙说:“至多10元”.小明说:“你们都猜错了.”则这本书的价格为( )
A.12元 B.13元 C.14元 D.无法确定
8.七年级(1)班的四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人只猜对一半,那么甲、乙、丙、丁的名次顺序为( )
A.甲、乙、丙、丁 B.甲、丙、乙、丁
C.甲、丁、乙、丙 D.甲、丙、丁、乙
9.甲、乙、丙三人用擂台赛形式进行乒乓球训练,每局2人进行比赛,另1人当裁判,每一局的输方去当下一局的裁判,而由原来的裁判向胜者挑战.半天训练结束时,发现甲共打了15局,乙共打了21局,而丙共当裁判5局,那么整个训练中的第5局的裁判是( )
A.甲 B.乙 C.丙 D.不确定
10.妈妈让小明给客人烧水沏茶,洗开水壶要用1分钟,烧开水要用15分钟,洗茶壶要用1分钟,洗茶杯要用1分钟,放茶叶要用2分钟,给同学打电话要用1分钟.为使客人早点喝上茶,小明最快可在几分钟内完成这些工作?( )
A.19分钟 B.18分钟 C.17分钟 D.16分钟
二、填空题
11.如图,下列条件①∠1=∠4,②∠2=∠3,③∠A+∠ABD=180°,④∠A+∠ACD=180°,⑤∠A=∠D,能判断AB∥CD的是 .(填序号)
12.如图,下列条件中:①∠BAD+∠ABC=180°;②∠1=∠2;③∠3=∠4;④∠BAD=∠BCD,能判定AD∥BC的是 .
13.如图,直线c与a,b相交,∠1=40°,∠2=70°,要使直线a与b平行,直线a顺时针旋转的度数至少是 °.
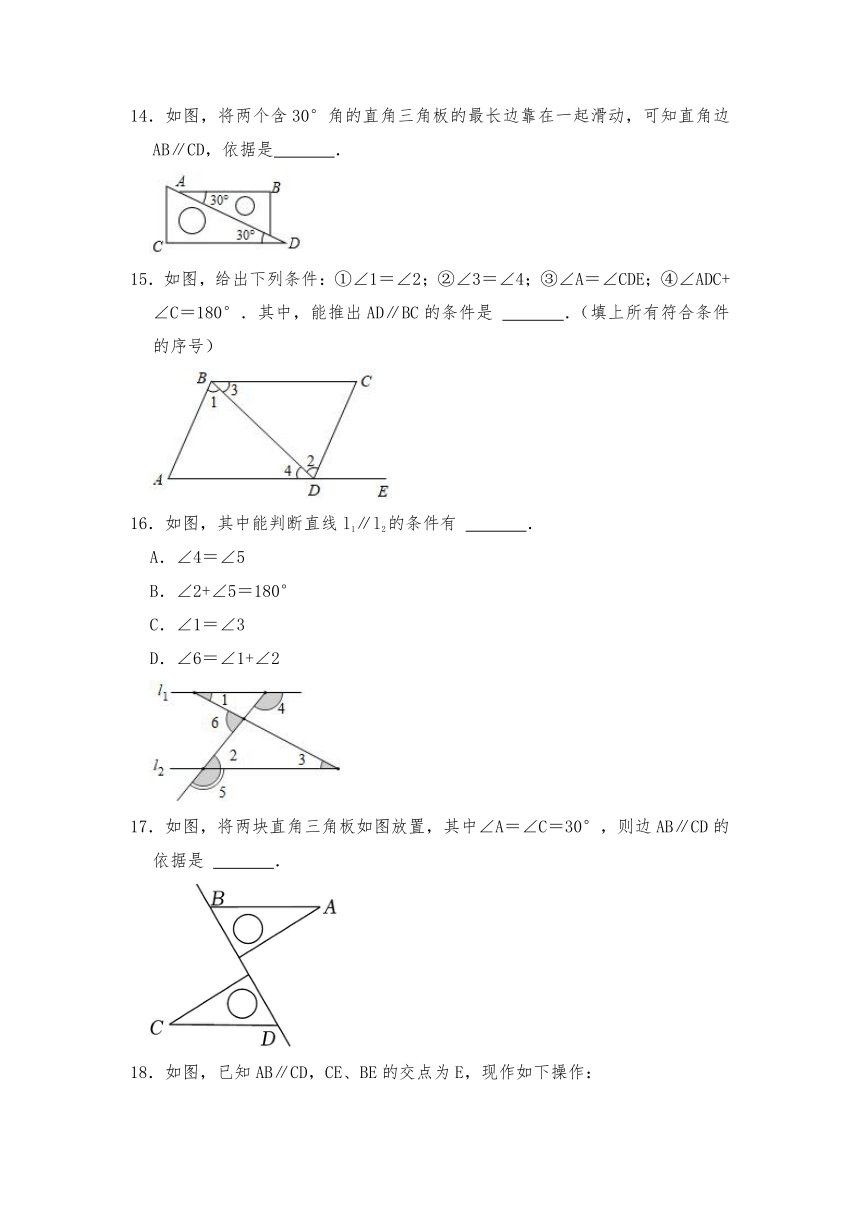
14.如图,将两个含30°角的直角三角板的最长边靠在一起滑动,可知直角边AB∥CD,依据是 .
15.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠ADC+∠C=180°.其中,能推出AD∥BC的条件是 .(填上所有符合条件的序号)
16.如图,其中能判断直线l1∥l2的条件有 .
A.∠4=∠5
B.∠2+∠5=180°
C.∠1=∠3
D.∠6=∠1+∠2
17.如图,将两块直角三角板如图放置,其中∠A=∠C=30°,则边AB∥CD的依据是 .
18.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,
…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于 度.
三、解答题
19.如图,有如下三个论断:
①AB∥CD;②∠1=∠2;③BE∥CF,以其中两个作为条件,另一个论断作为结论,组成一个真命题,并证明.
20.已知,一个角的两边与另一个角的两边分别平行,分别结合图探索这两个角的关系.
(1)如图1,AB∥EF,BC∥ED,∠1与∠2的关系是 .
证明:
(2)如图2,AB∥EF,BC∥DE,则∠1与∠2的关系是 .
证明:
(3)经过探索,综合上述,我们可以得一个真命题是 .
21.已知如图,BC与DE相交于点O,给出下面三个论断:①∠B=∠E;②AB∥DE;③BC∥EF.请以其中的两个论断为条件,填入“题设”栏中;剩下的论断为结论,
填入“结论”栏中,使之成为一个真命题,并加以证明.
题设:已知:如图,BC与DE相交于点O, , (填序号).
结论: (填序号).
证明:
22.(1)如图,设DE∥BC,∠1=∠3,CD⊥AB,求证:FG⊥AB;
(2)若把(1)的题设中的DE∥BC”与结论中的“FG⊥AB”对调后,命题还成立吗?说明理由;
(3)若把(1)的题设中的“∠1=∠3”与结论中的“FG⊥AB”对调后,命题还成立吗?说明理由.
23.真假命题的思考
一天,老师在黑板上写下了下列三个命题:
①垂直于同一条的直线的两条直线平行;
②若a2=b2,则a=b;
③若∠α和∠β的两边所在的直线分别平行,则∠α=∠β.
小明和小丽对话如下:
小明:“命题①是真命题,好像可以证明.”
小丽:“命题①是假命题,好像少了一些条件.”
(1)结合小明和小丽的对话,谈谈你的观点.如果你认为是真命题,请证明;如果你认为它是假命题,请增加一个适当的条件,使之成为真命题.
(2)请在命题②、③中选一个,如果你认为是真命题,请证明;如果你认为它是假命题,请举出反例.(选择命题②的,全部正确得2分,选择命题③的,全部正确得4分)
24.在数学课本中,有这样一道题:
如图1,AB∥CD,试用不同的方法证明∠B+∠C=∠BEC
(1)某同学写出了该命题的逆命题,请你帮他把逆命题的证明过程补充完整.
已知:如图1,∠B+∠C=∠BEC
求证:AB∥CD
证明:如图2,过点E,作EF∥AB
∴∠B=∠
∵∠B+∠C=∠BEC,∠BEF+∠FEC=∠BEC(已知)
∴∠B+∠C=∠BEF+∠FEC(等量代换)
∴∠ =∠ (等式性质)
∴EF∥
∵EF∥AB
∴AB∥CD(平行于同一条直线的两条直线互相平行)
(2)如图3,已知AB∥CD,在∠BCD的平分线上取两个点M、N,使得∠BMN=∠BNM,求证:∠CBM=∠ABN.
(3)如图4,已知AB∥CD,点E在BC的左侧,∠ABE,∠DCE的平分线相交于点F.请直接写出∠E与∠F之间的等量关系.
答案
一、选择题.
C.A.D.B.A.C.C.B.A.D.
二、填空题
11.①④.
12.①②③.
13.30.
14.内错角相等,两直线平行.
15.②④.
16.ACD.
17.内错角相等,两直线平行.
18.2n.
三、解答题
19.解:可以选①② ③.
即:若AB∥CD,∠1=∠2,则BE∥CF.
理由:∵AB∥CD,
∴∠ABC=∠DCB,
∵∠1=∠2,
∴∠EBC=∠FCB,
∴BE∥FC.
20.解:(1)∠1=∠2.
证明如下:∵AB∥CD,
∴∠1=∠3,
∵BE∥DF,
∴∠2=∠3,
∴∠1=∠2;
(2)∠1+∠2=180°.
证明如下:∵AB∥CD,
∴∠1=∠3,
∵BE∥DF,
∴∠2+∠3=180°,
∴∠1+∠2=180°;
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故答案为:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
21.解:题设:②、③;
结论:①;
证明过程如下:
∵AB∥DE,
∴∠B=∠COD,
又∵BC∥EF,
∴∠E=∠COD,
∴∠B=∠E.
故答案为②,③,①.
22.解:(1)∵DE∥BC,
∴∠1=∠2,
∵∠1=∠3,
∴∠2=∠3,
∴CD∥FG,
∵CD⊥AB,
∴FG⊥AB;
(2)成立,
理由是:∵FG⊥AB,CD⊥AB,
∴CD∥FG,
∴∠2=∠3,
∵∠1=∠3,
∴∠1=∠2,
∴DE∥BC;
(3)成立,
理由是:∵FG⊥AB,CD⊥AB,
∴CD∥FG,
∴∠2=∠3,
∵DE∥BC,
∴∠1=∠2,
∴∠1=∠3.
23.解:(1)①是假命题,增加“在同一平面内”这个条件,即可为真命题;
(2)②是假命题,反例:当a=1,b=﹣1时,a2=b2,但a≠b;
③是假命题,反例:如图,∠α和∠β的两边所在直线分别平行,∠α+∠β=180°,但∠α≠∠β;
24.(1)证明:如图2,过点E,作EF∥AB,
∴∠B=∠BEF,
∵∠B+∠C=∠BEC,∠BEF+∠FEC=∠BEC(已知),
∴∠B+∠C=∠BEF+∠FEC(等量代换),
∴∠C=∠CEF(等式性质),
∴EF∥CD,
∵EF∥AB,
∴AB∥CD(平行于同一条直线的两条直线互相平行);
故答案为:BEF,C,CEF,CD;
(2)证明:过点N作NG∥AB,交BM于点G,如图3所示:
则NG∥AB∥CD,
∴∠ABN=∠BNG,∠GNC=∠NCD,
∵∠BMN是△BCM的一个外角,
∴∠BMN=∠BCM+∠CBM,
又∵∠BMN=∠BNM,∠BNM=∠BNG+∠GNC,
∴∠BCM+∠CBM=∠BNG+∠GNC,
∴∠BCM+∠CBM=∠ABN+∠NCD,
∵CN平分∠BCD,
∴∠BCM=∠NCD,
∴∠CBM=∠ABN;
(3)解:∠BEC=2∠BFC,
理由:如图4,分别过E,F作EG∥AB,FH∥AB,则EG∥CD,FH∥CD,
∴∠BEG=∠ABE,∠CEG=∠DCE,
∴∠BEC=∠BEG+∠CEG=∠ABE+∠DCE,
同理可得∠BFC=∠ABF+∠DCF,
∵∠ABE,∠DCE的平分线相交于点F,
∴∠ABE=2∠ABF,∠DCE=2∠DCF,
∴∠BEC=2(∠ABF+∠DCF)=2∠BFC.
一、选择题.
1.如图,下列条件中,不能判定AB∥CD的是( )
A.∠D+∠BAD=180° B.∠1=∠2
C.∠3=∠4 D.∠B=∠DCE
2.如图,①∠1=∠3,②∠2=∠3,③∠1=∠4,④∠2+∠5=180°可以判定b∥c的条件有( )
A.①②④ B.①②③ C.②③④ D.①②③④
3.如图,BD平分∠ABC,若∠1=∠2,则( )
A.AD=BC B.AB=CD C.AB∥CD D.AD∥BC
4.如图,下列条件中,不能判定AD∥BC的是( )
A.∠1=∠2 B.∠BAD+∠ADC=180°
C.∠3=∠4 D.∠ADC+∠DCB=180°
5.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. B.
C. D.
6.如图,下列不能判定DE∥BC的条件是( )
A.∠B=∠ADE B.∠2=∠4
C.∠1=∠3 D.∠ACB+∠DEC=180°
7.小明花整数元网购了一本《趣数学》,让同学们猜书的价格.甲说:“至少15元”,乙说“至多13元”,丙说:“至多10元”.小明说:“你们都猜错了.”则这本书的价格为( )
A.12元 B.13元 C.14元 D.无法确定
8.七年级(1)班的四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人只猜对一半,那么甲、乙、丙、丁的名次顺序为( )
A.甲、乙、丙、丁 B.甲、丙、乙、丁
C.甲、丁、乙、丙 D.甲、丙、丁、乙
9.甲、乙、丙三人用擂台赛形式进行乒乓球训练,每局2人进行比赛,另1人当裁判,每一局的输方去当下一局的裁判,而由原来的裁判向胜者挑战.半天训练结束时,发现甲共打了15局,乙共打了21局,而丙共当裁判5局,那么整个训练中的第5局的裁判是( )
A.甲 B.乙 C.丙 D.不确定
10.妈妈让小明给客人烧水沏茶,洗开水壶要用1分钟,烧开水要用15分钟,洗茶壶要用1分钟,洗茶杯要用1分钟,放茶叶要用2分钟,给同学打电话要用1分钟.为使客人早点喝上茶,小明最快可在几分钟内完成这些工作?( )
A.19分钟 B.18分钟 C.17分钟 D.16分钟
二、填空题
11.如图,下列条件①∠1=∠4,②∠2=∠3,③∠A+∠ABD=180°,④∠A+∠ACD=180°,⑤∠A=∠D,能判断AB∥CD的是 .(填序号)
12.如图,下列条件中:①∠BAD+∠ABC=180°;②∠1=∠2;③∠3=∠4;④∠BAD=∠BCD,能判定AD∥BC的是 .
13.如图,直线c与a,b相交,∠1=40°,∠2=70°,要使直线a与b平行,直线a顺时针旋转的度数至少是 °.
14.如图,将两个含30°角的直角三角板的最长边靠在一起滑动,可知直角边AB∥CD,依据是 .
15.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠ADC+∠C=180°.其中,能推出AD∥BC的条件是 .(填上所有符合条件的序号)
16.如图,其中能判断直线l1∥l2的条件有 .
A.∠4=∠5
B.∠2+∠5=180°
C.∠1=∠3
D.∠6=∠1+∠2
17.如图,将两块直角三角板如图放置,其中∠A=∠C=30°,则边AB∥CD的依据是 .
18.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,
…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于 度.
三、解答题
19.如图,有如下三个论断:
①AB∥CD;②∠1=∠2;③BE∥CF,以其中两个作为条件,另一个论断作为结论,组成一个真命题,并证明.
20.已知,一个角的两边与另一个角的两边分别平行,分别结合图探索这两个角的关系.
(1)如图1,AB∥EF,BC∥ED,∠1与∠2的关系是 .
证明:
(2)如图2,AB∥EF,BC∥DE,则∠1与∠2的关系是 .
证明:
(3)经过探索,综合上述,我们可以得一个真命题是 .
21.已知如图,BC与DE相交于点O,给出下面三个论断:①∠B=∠E;②AB∥DE;③BC∥EF.请以其中的两个论断为条件,填入“题设”栏中;剩下的论断为结论,
填入“结论”栏中,使之成为一个真命题,并加以证明.
题设:已知:如图,BC与DE相交于点O, , (填序号).
结论: (填序号).
证明:
22.(1)如图,设DE∥BC,∠1=∠3,CD⊥AB,求证:FG⊥AB;
(2)若把(1)的题设中的DE∥BC”与结论中的“FG⊥AB”对调后,命题还成立吗?说明理由;
(3)若把(1)的题设中的“∠1=∠3”与结论中的“FG⊥AB”对调后,命题还成立吗?说明理由.
23.真假命题的思考
一天,老师在黑板上写下了下列三个命题:
①垂直于同一条的直线的两条直线平行;
②若a2=b2,则a=b;
③若∠α和∠β的两边所在的直线分别平行,则∠α=∠β.
小明和小丽对话如下:
小明:“命题①是真命题,好像可以证明.”
小丽:“命题①是假命题,好像少了一些条件.”
(1)结合小明和小丽的对话,谈谈你的观点.如果你认为是真命题,请证明;如果你认为它是假命题,请增加一个适当的条件,使之成为真命题.
(2)请在命题②、③中选一个,如果你认为是真命题,请证明;如果你认为它是假命题,请举出反例.(选择命题②的,全部正确得2分,选择命题③的,全部正确得4分)
24.在数学课本中,有这样一道题:
如图1,AB∥CD,试用不同的方法证明∠B+∠C=∠BEC
(1)某同学写出了该命题的逆命题,请你帮他把逆命题的证明过程补充完整.
已知:如图1,∠B+∠C=∠BEC
求证:AB∥CD
证明:如图2,过点E,作EF∥AB
∴∠B=∠
∵∠B+∠C=∠BEC,∠BEF+∠FEC=∠BEC(已知)
∴∠B+∠C=∠BEF+∠FEC(等量代换)
∴∠ =∠ (等式性质)
∴EF∥
∵EF∥AB
∴AB∥CD(平行于同一条直线的两条直线互相平行)
(2)如图3,已知AB∥CD,在∠BCD的平分线上取两个点M、N,使得∠BMN=∠BNM,求证:∠CBM=∠ABN.
(3)如图4,已知AB∥CD,点E在BC的左侧,∠ABE,∠DCE的平分线相交于点F.请直接写出∠E与∠F之间的等量关系.
答案
一、选择题.
C.A.D.B.A.C.C.B.A.D.
二、填空题
11.①④.
12.①②③.
13.30.
14.内错角相等,两直线平行.
15.②④.
16.ACD.
17.内错角相等,两直线平行.
18.2n.
三、解答题
19.解:可以选①② ③.
即:若AB∥CD,∠1=∠2,则BE∥CF.
理由:∵AB∥CD,
∴∠ABC=∠DCB,
∵∠1=∠2,
∴∠EBC=∠FCB,
∴BE∥FC.
20.解:(1)∠1=∠2.
证明如下:∵AB∥CD,
∴∠1=∠3,
∵BE∥DF,
∴∠2=∠3,
∴∠1=∠2;
(2)∠1+∠2=180°.
证明如下:∵AB∥CD,
∴∠1=∠3,
∵BE∥DF,
∴∠2+∠3=180°,
∴∠1+∠2=180°;
(3)如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
故答案为:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
21.解:题设:②、③;
结论:①;
证明过程如下:
∵AB∥DE,
∴∠B=∠COD,
又∵BC∥EF,
∴∠E=∠COD,
∴∠B=∠E.
故答案为②,③,①.
22.解:(1)∵DE∥BC,
∴∠1=∠2,
∵∠1=∠3,
∴∠2=∠3,
∴CD∥FG,
∵CD⊥AB,
∴FG⊥AB;
(2)成立,
理由是:∵FG⊥AB,CD⊥AB,
∴CD∥FG,
∴∠2=∠3,
∵∠1=∠3,
∴∠1=∠2,
∴DE∥BC;
(3)成立,
理由是:∵FG⊥AB,CD⊥AB,
∴CD∥FG,
∴∠2=∠3,
∵DE∥BC,
∴∠1=∠2,
∴∠1=∠3.
23.解:(1)①是假命题,增加“在同一平面内”这个条件,即可为真命题;
(2)②是假命题,反例:当a=1,b=﹣1时,a2=b2,但a≠b;
③是假命题,反例:如图,∠α和∠β的两边所在直线分别平行,∠α+∠β=180°,但∠α≠∠β;
24.(1)证明:如图2,过点E,作EF∥AB,
∴∠B=∠BEF,
∵∠B+∠C=∠BEC,∠BEF+∠FEC=∠BEC(已知),
∴∠B+∠C=∠BEF+∠FEC(等量代换),
∴∠C=∠CEF(等式性质),
∴EF∥CD,
∵EF∥AB,
∴AB∥CD(平行于同一条直线的两条直线互相平行);
故答案为:BEF,C,CEF,CD;
(2)证明:过点N作NG∥AB,交BM于点G,如图3所示:
则NG∥AB∥CD,
∴∠ABN=∠BNG,∠GNC=∠NCD,
∵∠BMN是△BCM的一个外角,
∴∠BMN=∠BCM+∠CBM,
又∵∠BMN=∠BNM,∠BNM=∠BNG+∠GNC,
∴∠BCM+∠CBM=∠BNG+∠GNC,
∴∠BCM+∠CBM=∠ABN+∠NCD,
∵CN平分∠BCD,
∴∠BCM=∠NCD,
∴∠CBM=∠ABN;
(3)解:∠BEC=2∠BFC,
理由:如图4,分别过E,F作EG∥AB,FH∥AB,则EG∥CD,FH∥CD,
∴∠BEG=∠ABE,∠CEG=∠DCE,
∴∠BEC=∠BEG+∠CEG=∠ABE+∠DCE,
同理可得∠BFC=∠ABF+∠DCF,
∵∠ABE,∠DCE的平分线相交于点F,
∴∠ABE=2∠ABF,∠DCE=2∠DCF,
∴∠BEC=2(∠ABF+∠DCF)=2∠BFC.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
