北师大版九年级数学上册第五章投影与视图单元复习题(含解析)
文档属性
| 名称 | 北师大版九年级数学上册第五章投影与视图单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 279.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 13:54:08 | ||
图片预览


文档简介
北师大版九年级数学上册第五章投影与视图单元复习题
一、单选题
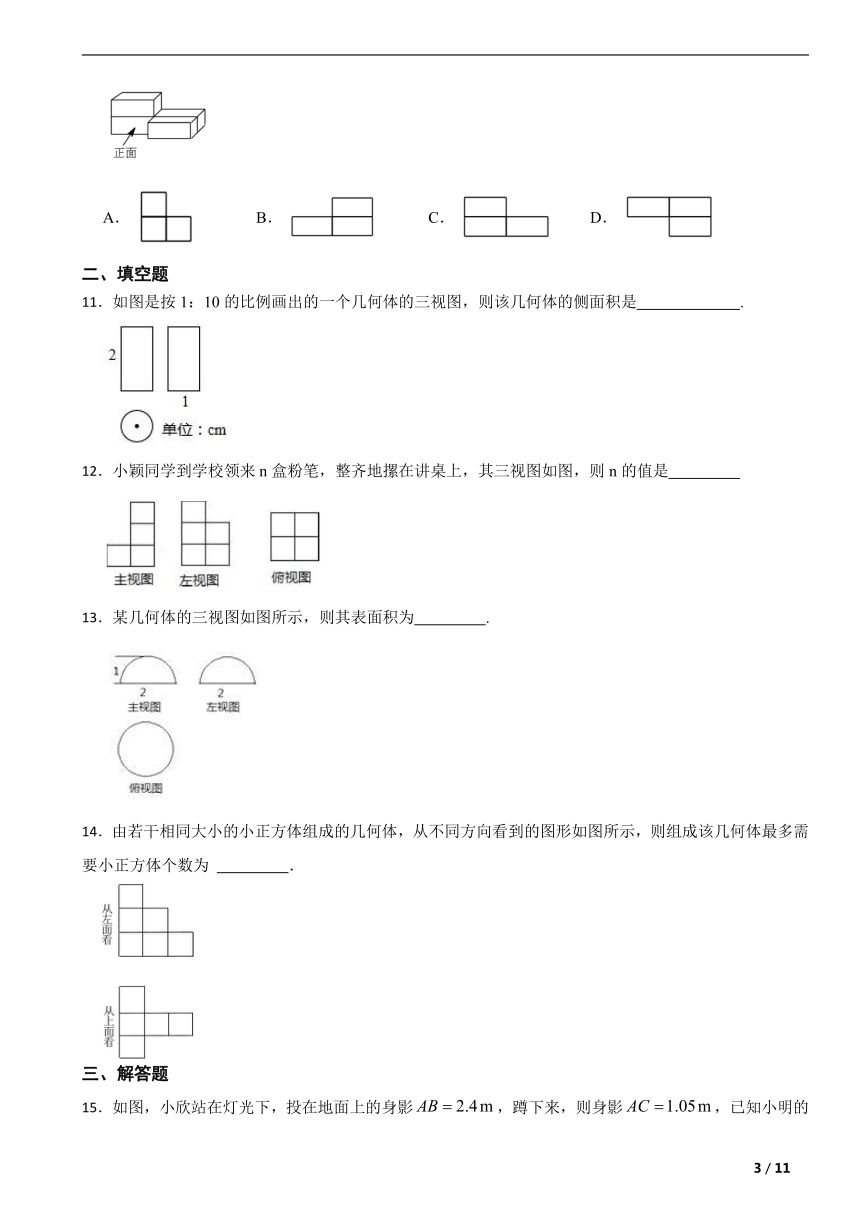
1.如图的三视图对应的物体是( )
A. B.
C. D.
2.如图所示几何体的左视图是( )
A. B. C. D.
3.如图所示的几何体的主视图是( )
A. B.
C. D.
4.如图所示的几何体是由5个大小相同的小立方块搭成,其左视图是( )
A. B. C. D.
5.一个几何体的主视图、左视图、俯视图都是长方形,这个几何体可能是( )
A.长方体 B.四棱锥 C.三棱锥 D.圆锥
6.若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为( )
A.4 B.4.5 C.5 D.5.5
7.如图,是由三个相同的小正方体组成的几何体,该几何体的俯视图是( )
A. B. C. D.
8.如图,几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )
A. B. C. D.
9.如图,将Rt△ABC绕直角边AB旋转一周,所得的几何体的主视图是( )
A. B. C. D.
10.左图是由4个相同的小长方体组成的立体图形,它的主视图是( )
A. B. C. D.
二、填空题
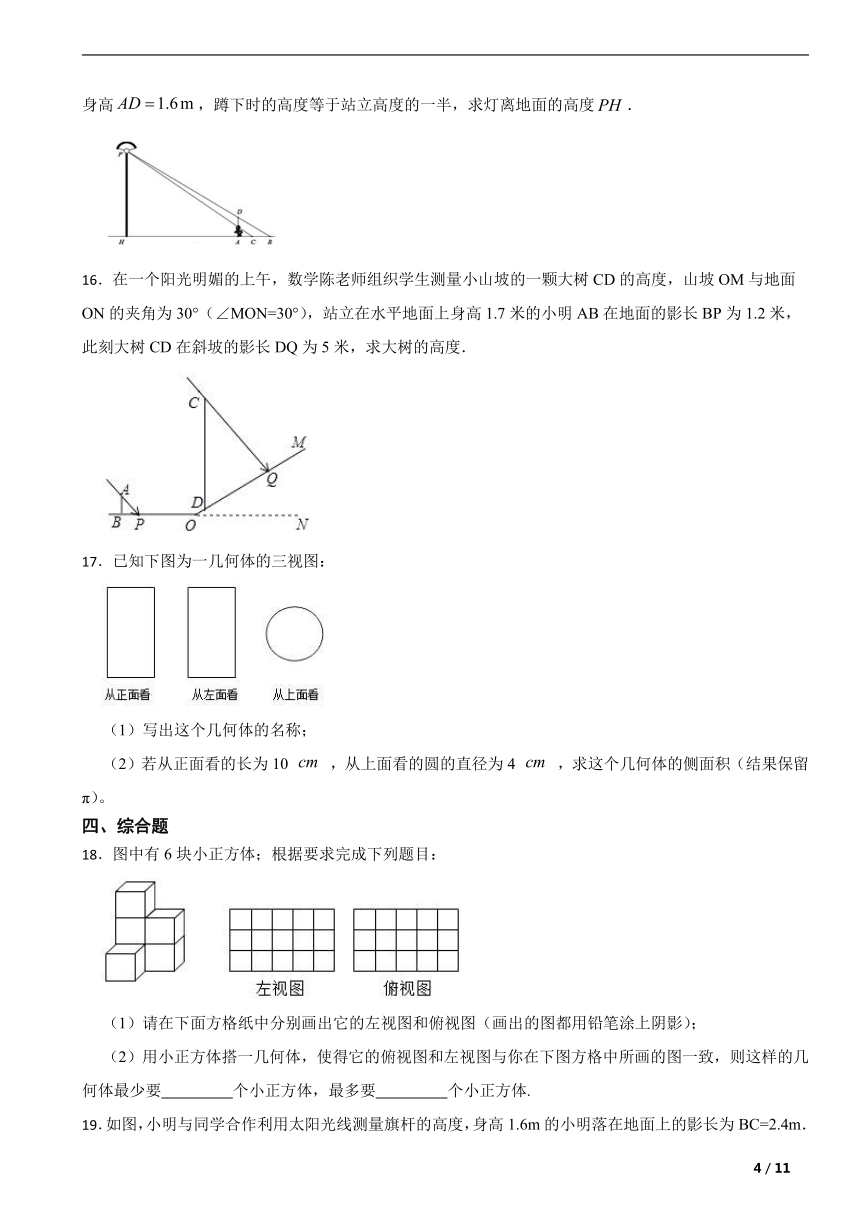
11.如图是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是 .
12.小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,其三视图如图,则n的值是
13.某几何体的三视图如图所示,则其表面积为 .
14.由若干相同大小的小正方体组成的几何体,从不同方向看到的图形如图所示,则组成该几何体最多需要小正方体个数为 .
三、解答题
15.如图,小欣站在灯光下,投在地面上的身影,蹲下来,则身影,已知小明的身高,蹲下时的高度等于站立高度的一半,求灯离地面的高度.
16.在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一颗大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.
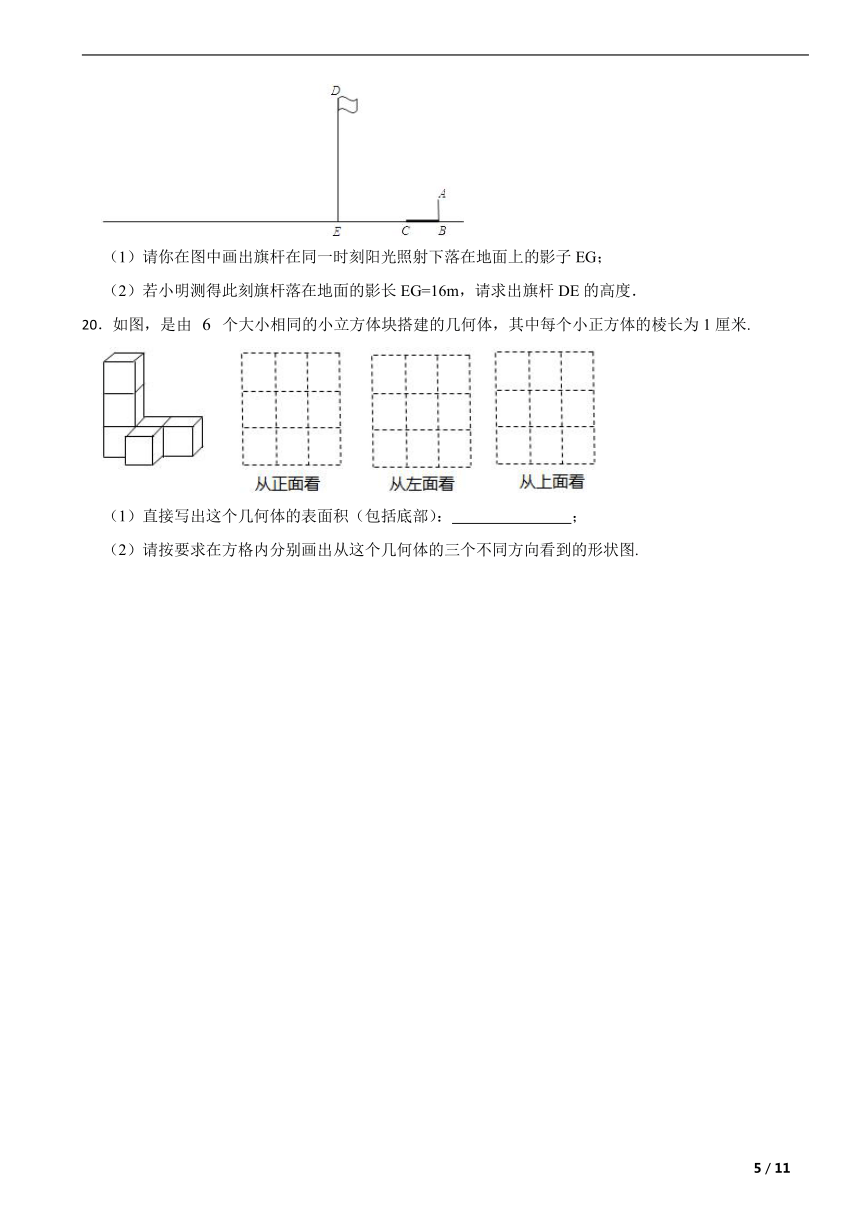
17.已知下图为一几何体的三视图:
(1)写出这个几何体的名称;
(2)若从正面看的长为10 ,从上面看的圆的直径为4 ,求这个几何体的侧面积(结果保留π)。
四、综合题
18.图中有6块小正方体;根据要求完成下列题目:
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图都用铅笔涂上阴影);
(2)用小正方体搭一几何体,使得它的俯视图和左视图与你在下图方格中所画的图一致,则这样的几何体最少要 个小正方体,最多要 个小正方体.
19.如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6m的小明落在地面上的影长为BC=2.4m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;
(2)若小明测得此刻旗杆落在地面的影长EG=16m,请求出旗杆DE的高度.
20.如图,是由 个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.
(1)直接写出这个几何体的表面积(包括底部): ;
(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
答案解析部分
1.【答案】D
【解析】【解答】解:从俯视图可知几何体的下面部分是三个长方形,三个长方形的宽度是相等的,
∴只有D选项符号.
故答案为:D
【分析】观察已知几何体的三视图可知从俯视图可知几何体的下面部分是三个长方形,三个长方形的宽度是相等的,据此可得答案.
2.【答案】C
【解析】【解答】解:从左边看是长方形,由几何体上边半圆凹槽底边看不见用虚线表示是C.
故答案为:C.
【分析】根据三视图的定义求解即可。
3.【答案】A
【解析】【解答】解:从正面可看到从左往右2列一个长方形和一个小正方形,
故答案为:A.
【分析】从几何体的正面观察,所看到的平面图形就是此几何体的主视图。
4.【答案】A
【解析】【解答】解:从主视图的左边往右边看得到的视图为
故答案为:A
【分析】根据左视图的定义,从主视图的左边往右边看得到的视图就是左视图,即可得到答案.
5.【答案】A
【解析】【解答】∵有2个视图是长方形,
∴该几何体为柱体,
∵第3个视图是长方形,
∴该几何体为长方体,
故答案为:A.
【分析】柱体一般有两个视图是长方形,椎体一般有两个视图是三角形,从而即可做出判断。
6.【答案】A
【解析】【解答】解:由三视图可知,该直六棱柱的高为1,
由俯视图得六棱柱的底面可分成两个相同的等腰梯形,且梯形的上、下底边长分别为1、3,高为1,
∴几何体的体积为 ×(1+3)×1×2×1=4,
故答案为:A.
【分析】由三视图可知,该直六棱柱的高为1,由俯视图得六棱柱的底面可分成两个相同的等腰梯形,且梯形的上、下底边长分别为1、3,高为1,再根据六棱柱的体积计算方法计算即可。
7.【答案】D
【解析】【解答】解:此几何体的俯视图为: .
故选D.
【分析】找到从上面看所得到的图形即可.
8.【答案】C
【解析】【解答】解:图中几何体的俯视图是C选项中的图形.
故选:C.
【分析】根据俯视图的概念和看得到的边都应用实线表现在三视图中、看不到,又实际存在的,又没有被其他边挡住的边用虚线表现在三视图中解答即可.
9.【答案】D
【解析】【解答】解:将Rt△ABC绕直角边AB旋转一周可得圆锥,圆锥的主视图是等腰三角形.
故选:D.
【分析】圆锥的主视图是从物体正面看,所得到的图形.
10.【答案】C
【解析】【解答】解:从正面看到的图形是两层,下层两个长方形排成一排,上层一个长方形,左对齐.
故答案为:C.
【分析】结合所给的几何体,再根据主视图的定义对每个选项一一判断即可。
11.【答案】200πcm2
【解析】【解答】观察三视图知:该几何体为圆柱,高为2,底面直径为1,
侧面积为:πdh=2×π=2π,
∵是按1:10的比例画出的一个几何体的三视图,
∴原几何体的侧面积=100×2π=200πcm,
故答案为:200πcm.
【分析】由已知的三视图可判断几何体是圆柱,根据圆柱的侧面积=长×宽可求解.
12.【答案】7
【解析】【解答】由俯视图可得最底层有4盒,由正视图和左视图可得第二层有2盒,第三层有1盒,共有7盒.
【分析】首先根据俯视图判断最底层的个数,然后结合主视图和左视图判断出该总盒数.
13.【答案】
【解析】【解答】解:由三视图可得该几何是一个半球体,
则其表面积为
故答案为。
【分析】由球的三视图都是圆可得,该几何体是一半球体,且半径为1.根据球体的表面积公式计算即可。
14.【答案】10
【解析】【解答】解:如图
在从上面看到的图上,借助于左侧视图分析:
最后一排有3层,
中间排要看到有2层,可以都是2个,此时需要正方体最多,(如果是211或121或112这样最少)
前面一排就有1层
最多有1+2+2+2+3=10个
故答案为:10
【分析】在理解三视图的定义的基础上,根据侧视图和俯视图,分析最少需要8个小正方体,最多需要10个小正方体。
15.【答案】解:如图,
∵AD∥PH,∴△ADB∽△HPB;△AMC∽△HPC(M是AD的中点),∴AB:HB=AD:PH,AC:AM=HC:PH,即2.4:(2.4+AH)=1.6:PH,1.05:0.8=(1.05+HA):PH,解得:AH=8.4,PH=7.2.
答:路灯的高度为7.2m.
【解析】【分析】先证明△AMC∽△HPC,再根据相似三角形的性质可得AC:AM=HC:PH,再将数据代入计算即可。
16.【答案】解:过点Q作QE⊥DC于点E,
由题意可得:△ABP∽△CEQ,
则 ,故 ,
可得:EQ∥NO,
则∠1=∠2=30°,
∵QD=5m,
∴DE= m,EQ= m,
故 = = ,
解得:EC= ,
故CE+DE= + = (m),
答:大树的高度为 m.
【解析】【分析】根据题意过点Q作QE⊥DC于点E,由题意可得:△ABP∽△CEQ,进而得出EQ,DE,EC的长,即可得出答案.
17.【答案】(1)解:这个几何体是圆柱。
(2)解:∵从正面看的长为10cm,从上面看的圆的直径为4cm,
∴该圆柱的底面直径为4,高为10,
∴该几何体的侧面积为2πrh=2π×2×10=40πcm2.
【解析】【分析】(1)根据几何体的三视图,将几何体还原为圆柱。
(2)根据题意确定圆柱的直径和高,然后求得其侧面积即可。
18.【答案】(1)解:如图所示:
(2)5;7
【解析】【解答】解:(2)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,
则这样的几何体最少要5个小立方块,最多要7个小立方块.
故答案为:5,7.
【分析】(1)主视图从左往右小正方形的个数为3,2;左视图从左往右小正方形的个数为3,1;俯视图从左往右小正方形的个数为2,1;
(2)由俯视图易得最底层小立方块的个数,由左视图找到其余层数里最少个数和最多个数相加即可.
19.【答案】(1)解:影子EG如图所示
(2)解:∵DG∥AC,
∴∠G=∠C,
∴Rt△ABC∽Rt△DGE,
∴ ,即 ,解得DE= ,
∴旗杆的高度为 m
【解析】【分析】(1)连结AC,过D点作DG∥AC交BC于G点,则GE为所求;(2)先证明Rt△ABC∽Rt△DGE,然后利用相似比计算DE的长.
20.【答案】(1)26平方厘米
(2)解:如图所示:
【解析】【解答】(1)这个几何体的表面积为:2×(5+4+4)×(1×1)=26(平方厘米)
故答案为:26平方厘米;
【分析】(1)根据几何体的形状计算出其表面积即可;
(2)观察实物图,利用三视图的画法,分别画出符合题意三个视图即可.
1 / 1
一、单选题
1.如图的三视图对应的物体是( )
A. B.
C. D.
2.如图所示几何体的左视图是( )
A. B. C. D.
3.如图所示的几何体的主视图是( )
A. B.
C. D.
4.如图所示的几何体是由5个大小相同的小立方块搭成,其左视图是( )
A. B. C. D.
5.一个几何体的主视图、左视图、俯视图都是长方形,这个几何体可能是( )
A.长方体 B.四棱锥 C.三棱锥 D.圆锥
6.若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为( )
A.4 B.4.5 C.5 D.5.5
7.如图,是由三个相同的小正方体组成的几何体,该几何体的俯视图是( )
A. B. C. D.
8.如图,几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )
A. B. C. D.
9.如图,将Rt△ABC绕直角边AB旋转一周,所得的几何体的主视图是( )
A. B. C. D.
10.左图是由4个相同的小长方体组成的立体图形,它的主视图是( )
A. B. C. D.
二、填空题
11.如图是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是 .
12.小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,其三视图如图,则n的值是
13.某几何体的三视图如图所示,则其表面积为 .
14.由若干相同大小的小正方体组成的几何体,从不同方向看到的图形如图所示,则组成该几何体最多需要小正方体个数为 .
三、解答题
15.如图,小欣站在灯光下,投在地面上的身影,蹲下来,则身影,已知小明的身高,蹲下时的高度等于站立高度的一半,求灯离地面的高度.
16.在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一颗大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.
17.已知下图为一几何体的三视图:
(1)写出这个几何体的名称;
(2)若从正面看的长为10 ,从上面看的圆的直径为4 ,求这个几何体的侧面积(结果保留π)。
四、综合题
18.图中有6块小正方体;根据要求完成下列题目:
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图都用铅笔涂上阴影);
(2)用小正方体搭一几何体,使得它的俯视图和左视图与你在下图方格中所画的图一致,则这样的几何体最少要 个小正方体,最多要 个小正方体.
19.如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6m的小明落在地面上的影长为BC=2.4m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;
(2)若小明测得此刻旗杆落在地面的影长EG=16m,请求出旗杆DE的高度.
20.如图,是由 个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为1厘米.
(1)直接写出这个几何体的表面积(包括底部): ;
(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.
答案解析部分
1.【答案】D
【解析】【解答】解:从俯视图可知几何体的下面部分是三个长方形,三个长方形的宽度是相等的,
∴只有D选项符号.
故答案为:D
【分析】观察已知几何体的三视图可知从俯视图可知几何体的下面部分是三个长方形,三个长方形的宽度是相等的,据此可得答案.
2.【答案】C
【解析】【解答】解:从左边看是长方形,由几何体上边半圆凹槽底边看不见用虚线表示是C.
故答案为:C.
【分析】根据三视图的定义求解即可。
3.【答案】A
【解析】【解答】解:从正面可看到从左往右2列一个长方形和一个小正方形,
故答案为:A.
【分析】从几何体的正面观察,所看到的平面图形就是此几何体的主视图。
4.【答案】A
【解析】【解答】解:从主视图的左边往右边看得到的视图为
故答案为:A
【分析】根据左视图的定义,从主视图的左边往右边看得到的视图就是左视图,即可得到答案.
5.【答案】A
【解析】【解答】∵有2个视图是长方形,
∴该几何体为柱体,
∵第3个视图是长方形,
∴该几何体为长方体,
故答案为:A.
【分析】柱体一般有两个视图是长方形,椎体一般有两个视图是三角形,从而即可做出判断。
6.【答案】A
【解析】【解答】解:由三视图可知,该直六棱柱的高为1,
由俯视图得六棱柱的底面可分成两个相同的等腰梯形,且梯形的上、下底边长分别为1、3,高为1,
∴几何体的体积为 ×(1+3)×1×2×1=4,
故答案为:A.
【分析】由三视图可知,该直六棱柱的高为1,由俯视图得六棱柱的底面可分成两个相同的等腰梯形,且梯形的上、下底边长分别为1、3,高为1,再根据六棱柱的体积计算方法计算即可。
7.【答案】D
【解析】【解答】解:此几何体的俯视图为: .
故选D.
【分析】找到从上面看所得到的图形即可.
8.【答案】C
【解析】【解答】解:图中几何体的俯视图是C选项中的图形.
故选:C.
【分析】根据俯视图的概念和看得到的边都应用实线表现在三视图中、看不到,又实际存在的,又没有被其他边挡住的边用虚线表现在三视图中解答即可.
9.【答案】D
【解析】【解答】解:将Rt△ABC绕直角边AB旋转一周可得圆锥,圆锥的主视图是等腰三角形.
故选:D.
【分析】圆锥的主视图是从物体正面看,所得到的图形.
10.【答案】C
【解析】【解答】解:从正面看到的图形是两层,下层两个长方形排成一排,上层一个长方形,左对齐.
故答案为:C.
【分析】结合所给的几何体,再根据主视图的定义对每个选项一一判断即可。
11.【答案】200πcm2
【解析】【解答】观察三视图知:该几何体为圆柱,高为2,底面直径为1,
侧面积为:πdh=2×π=2π,
∵是按1:10的比例画出的一个几何体的三视图,
∴原几何体的侧面积=100×2π=200πcm,
故答案为:200πcm.
【分析】由已知的三视图可判断几何体是圆柱,根据圆柱的侧面积=长×宽可求解.
12.【答案】7
【解析】【解答】由俯视图可得最底层有4盒,由正视图和左视图可得第二层有2盒,第三层有1盒,共有7盒.
【分析】首先根据俯视图判断最底层的个数,然后结合主视图和左视图判断出该总盒数.
13.【答案】
【解析】【解答】解:由三视图可得该几何是一个半球体,
则其表面积为
故答案为。
【分析】由球的三视图都是圆可得,该几何体是一半球体,且半径为1.根据球体的表面积公式计算即可。
14.【答案】10
【解析】【解答】解:如图
在从上面看到的图上,借助于左侧视图分析:
最后一排有3层,
中间排要看到有2层,可以都是2个,此时需要正方体最多,(如果是211或121或112这样最少)
前面一排就有1层
最多有1+2+2+2+3=10个
故答案为:10
【分析】在理解三视图的定义的基础上,根据侧视图和俯视图,分析最少需要8个小正方体,最多需要10个小正方体。
15.【答案】解:如图,
∵AD∥PH,∴△ADB∽△HPB;△AMC∽△HPC(M是AD的中点),∴AB:HB=AD:PH,AC:AM=HC:PH,即2.4:(2.4+AH)=1.6:PH,1.05:0.8=(1.05+HA):PH,解得:AH=8.4,PH=7.2.
答:路灯的高度为7.2m.
【解析】【分析】先证明△AMC∽△HPC,再根据相似三角形的性质可得AC:AM=HC:PH,再将数据代入计算即可。
16.【答案】解:过点Q作QE⊥DC于点E,
由题意可得:△ABP∽△CEQ,
则 ,故 ,
可得:EQ∥NO,
则∠1=∠2=30°,
∵QD=5m,
∴DE= m,EQ= m,
故 = = ,
解得:EC= ,
故CE+DE= + = (m),
答:大树的高度为 m.
【解析】【分析】根据题意过点Q作QE⊥DC于点E,由题意可得:△ABP∽△CEQ,进而得出EQ,DE,EC的长,即可得出答案.
17.【答案】(1)解:这个几何体是圆柱。
(2)解:∵从正面看的长为10cm,从上面看的圆的直径为4cm,
∴该圆柱的底面直径为4,高为10,
∴该几何体的侧面积为2πrh=2π×2×10=40πcm2.
【解析】【分析】(1)根据几何体的三视图,将几何体还原为圆柱。
(2)根据题意确定圆柱的直径和高,然后求得其侧面积即可。
18.【答案】(1)解:如图所示:
(2)5;7
【解析】【解答】解:(2)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,
则这样的几何体最少要5个小立方块,最多要7个小立方块.
故答案为:5,7.
【分析】(1)主视图从左往右小正方形的个数为3,2;左视图从左往右小正方形的个数为3,1;俯视图从左往右小正方形的个数为2,1;
(2)由俯视图易得最底层小立方块的个数,由左视图找到其余层数里最少个数和最多个数相加即可.
19.【答案】(1)解:影子EG如图所示
(2)解:∵DG∥AC,
∴∠G=∠C,
∴Rt△ABC∽Rt△DGE,
∴ ,即 ,解得DE= ,
∴旗杆的高度为 m
【解析】【分析】(1)连结AC,过D点作DG∥AC交BC于G点,则GE为所求;(2)先证明Rt△ABC∽Rt△DGE,然后利用相似比计算DE的长.
20.【答案】(1)26平方厘米
(2)解:如图所示:
【解析】【解答】(1)这个几何体的表面积为:2×(5+4+4)×(1×1)=26(平方厘米)
故答案为:26平方厘米;
【分析】(1)根据几何体的形状计算出其表面积即可;
(2)观察实物图,利用三视图的画法,分别画出符合题意三个视图即可.
1 / 1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
