北师大版九年级数学下册第二章二次函数单元复习题(含解析)
文档属性
| 名称 | 北师大版九年级数学下册第二章二次函数单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 344.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 13:55:14 | ||
图片预览




文档简介
北师大版九年级数学下册第二章二次函数单元复习题
一、单选题
1.下列函数关系中,y是x的二次函数的是( ).
A. B. C. D.
2.抛物线的顶点坐标是( )
A. B. C. D.
3.二次函数 的对称轴是( )
A. B. C. D.
4.将抛物线 向下平移2个单位长度,得到的抛物线为( )
A. B. C. D.
5.若 是二次函数,则m的值为( )
A.2 B.-2 C.2或-2 D.0
6.如图,函数y=ax2-2x+1和y=ax-a(a是常数,且a≠0)在同一个平面直角坐标系中的图象可能是( )
A. B. C. D.
7.下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A.y=(x-2)2+1 B.y=(x+2)2+1
C.y=(x-2)2-3 D.y=(x+2)2-3
8.二次函数y=ax2+bx+c(a≠0)的图象如图,以下结论正确的是( )
A.abc>0 B.方程ax2+bx+c=0有两个实数根分别为-2和6
C.a-b+c<0 D.当y=4时,x的取值只能为0
9.若二次函数y=x2﹣6x+k的图象经过A(﹣1,y1),B(1,y2),C(3+ ,y3)三点,则y1,y2,y3关系正确的是( )
A.y1>y2>y3 B.y1>y3>y2 C.y2>y1>y3 D.y3>y1>y2
10.二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(﹣1,0).设t=a+b+1,则t值的变化范围是( )
A.0<t<1 B.0<t<2 C.1<t<2 D.﹣1<t<1
二、填空题
11.已知A(-1,3),B(2,3)是抛物线y=ax2+bx+c(a≠0)上两点,该抛物线的对称轴是直线 .
12.已知二次函数 的图象如图所示,若方程 有两个不相等的实数根,则 的取值范围是 。
13.抛物线y=-x2+15有最 值,顶点坐标是 .
14.已知抛物线 过点 ,与 轴和直线 分别相交于点A、B,点 为抛物线上A,B两点之间(包含A,B两点)的一个动点,若 ,则b的取值范围为 .
三、解答题
15.已知将成本为40元的某种商品按50元的定价售出时,能卖出500个,如果该种商品每涨价1元,其销售量就要减少20个,如何定价才能获得最大收益?
16.如图,请根据图中信息,求出这个二次函数解析式:
17.在同一坐标系中,画出函数y1=2x2,y2=2(x-2)2与y3=2(x+2)2的图象,并说明y2,y3的图象与y1=2x2的图象的关系.
18.如图,在平面直角坐标系中,抛物线经过A(-1,0),B(4,0),C(0,-4),⊙M是△ABC的外接圆,M为圆心。
⑴求抛物线的解析式;
⑵求阴影部分的面积;
⑶在正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=K,△CPQ的面积为S,求S关于K的函数关系式,并求出S的最大值。
四、综合题
19.已知函数y=-(m+2) (m为常数),求当m为何值时:
(1)y是x的一次函数
(2)y是x的二次函数 并求出此时纵坐标为-8的点的坐标.
20.如图,排球运动员站在点O处练习发球,将球从O点正上方的A处发出,把球看成点,其运行的高度与运行的水平距离满足关系式.已知球网与O点的水平距离为,高度为,球场的边界距O点的水平距离为.
(1)当时,求y与x的关系式(不要求写出自变量x的取值范围);
(2)当时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
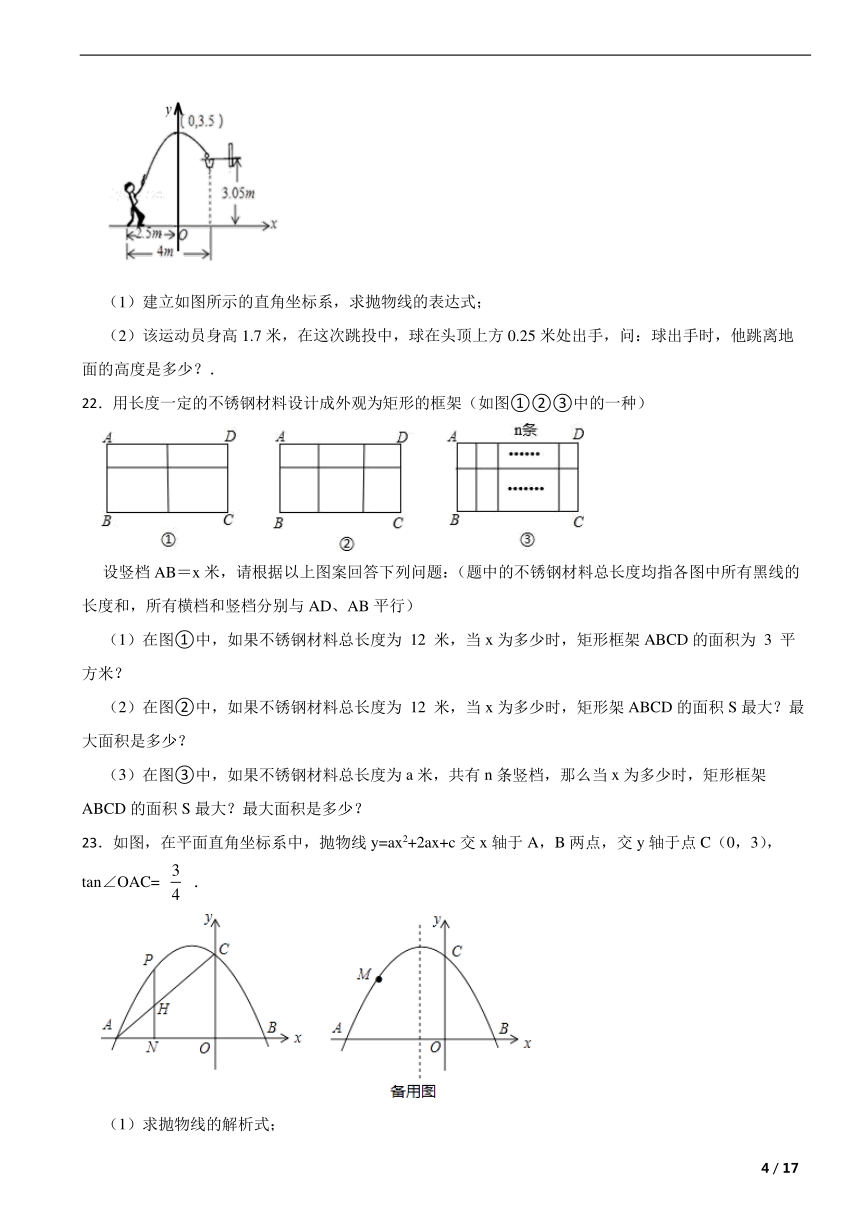
21.如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)该运动员身高1.7米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?.
22.用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种)
设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
(1)在图①中,如果不锈钢材料总长度为 12 米,当x为多少时,矩形框架ABCD的面积为 3 平方米?
(2)在图②中,如果不锈钢材料总长度为 12 米,当x为多少时,矩形架ABCD的面积S最大?最大面积是多少?
(3)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,那么当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
23.如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC= .
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】C
【解析】【解答】解:选项A中, 不是二次函数,故选项A错误;
选项B中, 不是二次函数,故选项B错误;
选项C中, 是二次函数,故选项C正确;
选项D中, 不是二次函数,故选项D错误.
故答案为:C.
【分析】形如“y=ax2+bx+c(a、b、c是常数,且a≠0)”的函数就是二次函数,据此判断.
2.【答案】A
【解析】【解答】解:∵,
∴此函数的顶点坐标为(3,1),
故答案为:A.
【分析】根据二次函数的图象与性质求解即可。
3.【答案】D
【解析】【解答】∵二次函数解析式是
∴对称轴是直线
故答案为:D
【分析】根据二次函数顶点式的性质直接写出对称轴即可。
4.【答案】B
【解析】【解答】由抛物线平移的规律,可得将抛物线y=2x2向下平移2个单位后所得到的抛物线为,
故答案为:B.
【分析】利用抛物线的平移规律即可写出表达式。
5.【答案】B
【解析】【解答】解:根据题意的得:
解得:
∴m=-2,
故答案为:B.
【分析】根据二次函数的定义,令x的指数为2,系数不为0,列出方程与不等式解答即可.
6.【答案】C
【解析】【解答】解:A、由一次函数y=ax-a的图象可得:a>0,此时一次函数y=ax-a的图象与y轴相交于负半轴,二次函数y=ax2-2x+1的图象开口向上,对称轴x=->0,故选项A错误;
B、由一次函数y=ax-a的图象可得:a<0,此时二次函数y=ax2-2x+1的图象开口向下,故选项B错误;
C、由一次函数y=ax-a的图象可得:a<0,此时二次函数y=ax2-2x+1的图象开口向下,对称轴x=-<0,故选项C正确;
D、由一次函数y=ax-a的图象可得:a<0,此时二次函数y=ax2-2x+1的图象开口向下,对称轴x=-<0,故选项D错误.
故答案为:C.
【分析】 先根据一次函数的图象判断a的符号,再判断二次函数图象与实际是否相符,然后判断正误,即可得出答案.
7.【答案】C
【解析】【分析】采用逐一排除的方法.先根据对称轴为直线x=2排除B、D,再将点(0,1)代入A、C两个抛物线解析式检验即可.
【解答】∵抛物线对称轴为直线x=2,
∴可排除B、D选项,
将点(0,1)代入A中,得(x-2)2+1=(0-2)2+1=5,故A选项错误,
代入C中,得(x-2)2-3=(0-2)2-3=1,故C选项正确.
故选:C.
【点评】本题考查了二次函数的性质.关键是根据对称轴,点的坐标与抛物线解析式的关系,逐一排除.
8.【答案】B
【解析】【解答】因为
二次函数y=ax2+bx+c(a≠0 )与x轴交于点(-2,0)、(6,0),故方程
ax2+bx+c=0的两个实数根为-2和6。
故答案为:B。
【分析】抛物线开口向下故a<0,对称轴在y轴右侧,a、b异号,与y轴交于点(0,4),故c=4,abc<0;抛物线y=ax2+bx+c(a≠0 )与x轴交点的横坐标就是方程ax2+bx+c=0的解;当x=-1时,抛物线上点在x轴上方,故a-b+c>0,当y=4时,根据函数的对称性,x的取值为0或4。
9.【答案】A
【解析】【解答】解:∵y=x2﹣6x+k,
∴图象的开口向上,对称轴是直线x= =3,
C(3+ ,y3)关于直线x=3的对称点是(3- ,y3),
∵ 1<1<3- ,
∴y1>y2>y3,
故答案为:A.
【分析】先求出二次函数的队曾在,再求出点A、B、C到对称轴的距离,再根据二次函数增减性判断即可。
10.【答案】B
【解析】【分析】由二次函数的解析式可知,当x=1时,所对应的函数值y=t=a+b+1.把点(-1,0)代入y=ax2+bx+1,a-b+1=0,然后根据顶点在第一象限,可以画出草图并判断出a与b的符号,进而求出t=a+b+1的变化范围.
【解答】∵二次函数y=ax2+bx+1的顶点在第一象限,
且经过点(-1,0),
∴易得:a-b+1=0,a<0,b>0,
由a=b-1<0得到b<1,结合上面b>0,所以0<b<1①,
由b=a+1>0得到a>-1,结合上面a<0,所以-1<a<0②,
∴由①+②得:-1<a+b<1,
在不等式两边同时加1得0<a+b+1<2,
∵a+b+1=t代入得0<t<2,
∴0<t<2.
故选:B
【点评】此题主要考查了二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特殊点的关系,也要掌握在图象上表示一元二次方程ax2+bx+c=0的解的方法.同时注意特殊点的运用.
11.【答案】
【解析】【解答】解:A(-1,3),B(2,3)是抛物线y=ax2+bx+c(a≠0)上两点,
抛物线的对称轴为
故答案为: .
【分析】根据抛物线的对称性进行解答即可.
12.【答案】
【解析】【解答】解:由图象可知:二次函数y=ax2+bx+c的顶点坐标为(1,5),
∴ =5,即b2-4ac=-20a,
∵ax2+bx+c=k有两个不相等的实数根,
∴方程ax2+bx+c-k=0的判别式△>0,即b2-4a(c-k)=b2-4ac+4ak=-20a+4ak=-4a(5-k)>0
∵抛物线开口向下
∴a<0
∴5-k>0
∴k<5.
故答案为:k<5.
【分析】根据二次函数的一般形式的顶点坐标为(,),可得b2-4ac=-20a,再根据一元二次方程的根的判别式可得,结合抛物线开口向下确定a的符号,即可求解。
13.【答案】大;(0,15)
【解析】【解答】解:∵ 抛物线y=-x2+15
a=-1<0
∴抛物线开口向下,则抛物线y=-x2+15有最大值,顶点坐标为:(0,15)
故答案为:大;(0,15)
【分析】根据函数解析式,由a<0可知抛物线开口向下,抛物线有最高点,则函数有最大值;再求出顶点坐标。
14.【答案】b≤-4
【解析】【解答】解:将点 代入 得:
,
整理得: ,
,
,解得 ,
则抛物线的解析式为 ,
当 时, ,即 ,
当 时, ,即 ,
点 为抛物线上A,B两点之间(包含A,B两点)的一个动点,且 ,
,
解得 ,
故答案为:b≤-4.
【分析】先将点代入函数,整理得到a=1, 则抛物线为y=x2+bx 3,所以抛物线开口向上,接着求出A、B的坐标,最后根据进而即可求出答案.
15.【答案】解:设售价为x元,获得的利润为y元,则销售个数为500-20(x-50),
由题意得,
y=(x-40)×(500-20x+1000)
=-20(x-40)(x-75)
=-20(x2-115x+3000)
=-20(x-57.5)2-60000+66125
=-20(x-57.5)2+6125
答:当x=57.5元时得到最大利益6125元.
【解析】【分析】设售价为x元,获得的利润为y元,根据题意列出函数解析式y=(x-40)×(500-20x+1000)=-20(x-57.5)2+6125,再利用二次函数的性质求解即可。
16.【答案】解:由图可知,图象过(-1, 0)、(2, 0)、(0, -2)三点,
设这个二次函数解析式为y=ax2 +bx+c(a≠0),把以上三点代入解析式得:
解得:
∴这个二次函数解析式为y=x2-x+2;
【解析】【分析】观察图象得出抛物线经过(-1, 0)、(2, 0)、(0, 2)三点, 设这个二次函数解析式为y=ax2+bx+c代入抛物线的解析式得出关于a,b,c的方程组,解方程组得出a,b,c的值,即可得出答案.
17.【答案】解:如图,
y2的图象由y1=2x2的图象向右平移2个单位得到;
y3的图象由y1=2x2的图象向左平移2个单位得到.
【解析】【分析】由图像可知:向右平移2个单位长度可得抛物线;向左平移2个单位长度可得抛物线。
18.【答案】解:(1)由抛物线经过A(-1,0),B(4,0),
设抛物线的解析式为:y=a(x+1)(x-4),
将C(0,-4)代入上式中,得-4a=-4,a=1.
∴y=(x+1)(x-4)=x2-3x-4.
(2)∵A(-1,0),B(4,0),C(0,-4).
∴OB=OC=4,OA=1
∴∠OBC=45°,∴∠AMC=90°
∴AM2+MC2=OA2+OC2=12+42=17
∴AM2=CM2=,
∴S阴影=.
(3)∠OBC=45°,PQ⊥x轴;
∴BP=PQ=k,
∴S=k (4-k)=-k2+2k.
∴当k=2时,S最大值=2.
【解析】【分析】
(1)已知了A、B、C三点坐标可用待定系数法求出抛物线的解析式.
(2)要求扇形的面积需要知道半径的长和扇形的圆心角的度数,先求圆心角∠AMC的度数,由于OB=OC,因此∠ABC=45°,根据圆周角定理可得出∠AMC=90°.再求半径,由于三角形AMC是等腰直角三角形,因此半径的平方等于AC的平方的一半,可在直角三角形OAC中求出AC的平方,据此可根据扇形的面积公式求出扇形的面积.
(3)求三角形CPQ的面积可以PQ为底,以OP为高,已知了PQ=k,在等腰直角三角形BPQ中,BP=PQ=k,也就能表示长OP的长,据此可求出S与k的函数关系,根据函数的性质即可求出S的最大值.
19.【答案】(1)由y=-(m+2) (m为常数),y是x的一次函数,得 解得m=± ,当m=± 时,y是x的一次函数.
(2)由y=-(m+2) (m为常数),y是x的二次函数,得 解得m=2,m=-2(错误的要舍去),当m=2时,y是x的二次函数,当y=-8时,-8=-4x2,解得x=± ,故纵坐标为-8的点的坐标是(± ,-8).
【解析】【分析】(1)根据形如y=kx(,k是常数)是一次函数,可得出一次函数;
(2)根据根据形如(是常数,)是二次函数,可得答案,根据函数值,得出自变量的值,即可得出符合条件的点。
20.【答案】(1)解:由图象可知:点A的坐标为
将点和代入解析式中,得
,解得:
∴y与x的关系式为.
(2)解:球能越过球网,球不会出界,理由如下
将代入中,得
,
∴球能越过球网;
将代入中,得
,
∴该抛物线与x轴的右交点必在(18,0)的左侧,
∴球不会出界,
综上:球能越过球网,球不会出界.
(3)解:将点代入解析式中,得:
解得:
∴抛物线的解析式为
若球一定能越过球网,则当时, ;
∴,解得:
若不出边界,即抛物线与x轴的右交点在的左侧或重合,即当时,;
∴,解得
综上:若球一定能越过球网,又不出边界,h的取值范围为.
【解析】【分析】(1)由题意得A(0,2),将点A(0,2)及h=2.8分别代入y=a(x-6)2+h可求出a的值,从而得出y关于x的函数解析式;
(2)将x=9代入(1)所求的函数解析式算出对应的函数值,再将该值与2.45比大小即可判断得出球是否过网;将x=9代入(1)所求的函数解析式算出对应的函数值,再将该值与0比大小即可判断得出球是否出界;
(3)将点A(0,2)代入y=a(x-6)2+h可表示出a的值为 ,得抛物线的解析式为, 若球一定能越过球网,则当x=9时, y>2.45,据此建立不等式求解得出h的取值范围, 若不出边界,即抛物线与x轴的右交点在(18,0)的左侧或重合,即当x=18时,y≤0,据此建立不等式,求解可得h的取值范围,综上即可得出答案.
21.【答案】(1)解:抛物线的顶点坐标为(0,3.5),
∴设抛物线的表达式为y=ax2+3.5,
由图可知函数图象过点(1.5,3.05),
∴2.25a+3.5=3.05,
解得:a=-0.2,
∴抛物线的表达式为y= - 0.2x2+3.5;
(2)解:设球出手时,他跳离地面的高度为hm,则球出手时,球的高度为(h+1.7+0.25)m,
∵(1)中求得y= - 0.2x2+3.5,
∴ ,
解得:h=0.3,
答:球出手时,他跳离地面的高度为0.3m.
【解析】【分析】(1)设抛物线的表达式为y=ax2+3.5,依题意可知函数图象经过点(1.5,3.05),代入可得a的值;(2)设球出手时,他跳离地面的高度为hm,则可得 ,解方程求出h即可.
22.【答案】(1)解: AD= ,
由题意得: ,
,
∴ ,
答:当 或3米时,矩形框架ABCD的面积为3平方米;
(2)解: ,
,
,
当 时,
4 ,
答:当 时,矩形架ABCD的面积S最大,最大面积是3平方米;
(3)解: ,
,
,
当 时
.
答:当 时,矩形ABCD的面积S最大,最大面积是 平方米.
【解析】【分析】(1)由题意可得3AD+3AB=12,从而可得出AD的表达式;根据矩形的面积=长×宽,可得出方程;(2)由题意可得3AD+4AB=12,从而可得出AD的表达式;根据矩形的面积=长×宽,可得出S与x的函数关系式;(3)由题意可得3AD+nAB=a,从而可得出AD的表达式,根据矩形的面积=长×宽,可得出S与x的函数关系式,利用配方法可求出S的最大值.
23.【答案】(1)解:∵C(0,3),
∴OC=3,
∵tan∠OAC= ,
∴OA=4,
∴A(﹣4,0).
把A(﹣4,0)、C(0,3)代入y=ax2+2ax+c中,
得 ,解得: ,
∴抛物线的解析式为y=﹣ x2﹣ x+3
(2)解:设直线AC的解析式为y=kx+b,
把A(﹣4,0)、C(0,3)代入y=kx+b中,
得: ,解得: ,
∴直线AC的解析式为y= x+3.
设N(x,0)(﹣4<x<0),则H(x, x+3),P(x,﹣ x2﹣ x+3),
∴PH=﹣ x2﹣ x+3﹣( x+3)=﹣ x2﹣ x=﹣ (x+2)2+ ,
∵﹣ <0,
∴PH有最大值,
当x=﹣2时,PH取最大值,最大值为
(3)解:过点M作MK⊥y轴于点K,交对称轴于点G,则∠MGE=∠MKC=90°,
∴∠MEG+∠EMG=90°,
∵四边形CMEF是正方形,
∴EM=MC,∠MEC=90°,
∴∠EMG+∠CMK=90°,
∴∠MEG=∠CMK.
在△MCK和△MEG中, ,
∴△MCK≌△MEG(AAS),
∴MG=CK.
由抛物线的对称轴为x=﹣1,设M(x,﹣ x2﹣ x+3),则G(﹣1,﹣ x2﹣ x+3),K(0,﹣ x2﹣ x+3),
∴MG=|x+1|,CK=|﹣ x2﹣ x+3﹣3|=|﹣ x2﹣ x|=| x2+ x|,
∴|x+1|=| x2+ x|,
∴ x2+ x=±(x+1),
解得:x1=﹣4,x2=﹣ ,x3=﹣ ,x4=2,
代入抛物线解析式得:y1=0,y2= ,y3= ,y4=0,
∴点M的坐标是(﹣4,0),(﹣ , ),(﹣ , )或(2,0).
【解析】【分析】(1)由点C的坐标以及tan∠OAC= 可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;(2)设直线AC的解析式为y=kx+b,由点A、C的解析式利用待定系数法即可求出直线AC的解析式,设N(x,0)(﹣4<x<0),可找出H、P的坐标,由此即可得出PH关于x的解析式,利用配方法即二次函数的性质即可解决最值问题;(3)过点M作MK⊥y轴于点K,交对称轴于点G,根据角的计算依据正方形的性质即可得出△MCK≌△MEG(AAS),进而得出MG=CK.设出点M的坐标利用正方形的性质即可得出点G、K的坐标,由正方形的性质即可得出关于x的含绝对值符号的一元二次方程,解方程即可求出x值,将其代入抛物线解析式中即可求出点M的坐标.本题考查了待定系数法求函数解析式、二次函数的性质、正方形的性质以及全等三角形的判定与性质,解题的关键是:(1)利用待定系数法求出抛物线解析式;(2)根据二次函数的性质解决最值问题;(3)根据正方形的性质得出关于x的含绝对值符号的一元二次方程.本题属于中档题,难度不大,解决该题型题目时,根据正方形的性质找出关于x的含绝对值符号的一元二次方程,解方程求出点的横坐标是关键.
1 / 1
一、单选题
1.下列函数关系中,y是x的二次函数的是( ).
A. B. C. D.
2.抛物线的顶点坐标是( )
A. B. C. D.
3.二次函数 的对称轴是( )
A. B. C. D.
4.将抛物线 向下平移2个单位长度,得到的抛物线为( )
A. B. C. D.
5.若 是二次函数,则m的值为( )
A.2 B.-2 C.2或-2 D.0
6.如图,函数y=ax2-2x+1和y=ax-a(a是常数,且a≠0)在同一个平面直角坐标系中的图象可能是( )
A. B. C. D.
7.下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A.y=(x-2)2+1 B.y=(x+2)2+1
C.y=(x-2)2-3 D.y=(x+2)2-3
8.二次函数y=ax2+bx+c(a≠0)的图象如图,以下结论正确的是( )
A.abc>0 B.方程ax2+bx+c=0有两个实数根分别为-2和6
C.a-b+c<0 D.当y=4时,x的取值只能为0
9.若二次函数y=x2﹣6x+k的图象经过A(﹣1,y1),B(1,y2),C(3+ ,y3)三点,则y1,y2,y3关系正确的是( )
A.y1>y2>y3 B.y1>y3>y2 C.y2>y1>y3 D.y3>y1>y2
10.二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(﹣1,0).设t=a+b+1,则t值的变化范围是( )
A.0<t<1 B.0<t<2 C.1<t<2 D.﹣1<t<1
二、填空题
11.已知A(-1,3),B(2,3)是抛物线y=ax2+bx+c(a≠0)上两点,该抛物线的对称轴是直线 .
12.已知二次函数 的图象如图所示,若方程 有两个不相等的实数根,则 的取值范围是 。
13.抛物线y=-x2+15有最 值,顶点坐标是 .
14.已知抛物线 过点 ,与 轴和直线 分别相交于点A、B,点 为抛物线上A,B两点之间(包含A,B两点)的一个动点,若 ,则b的取值范围为 .
三、解答题
15.已知将成本为40元的某种商品按50元的定价售出时,能卖出500个,如果该种商品每涨价1元,其销售量就要减少20个,如何定价才能获得最大收益?
16.如图,请根据图中信息,求出这个二次函数解析式:
17.在同一坐标系中,画出函数y1=2x2,y2=2(x-2)2与y3=2(x+2)2的图象,并说明y2,y3的图象与y1=2x2的图象的关系.
18.如图,在平面直角坐标系中,抛物线经过A(-1,0),B(4,0),C(0,-4),⊙M是△ABC的外接圆,M为圆心。
⑴求抛物线的解析式;
⑵求阴影部分的面积;
⑶在正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=K,△CPQ的面积为S,求S关于K的函数关系式,并求出S的最大值。
四、综合题
19.已知函数y=-(m+2) (m为常数),求当m为何值时:
(1)y是x的一次函数
(2)y是x的二次函数 并求出此时纵坐标为-8的点的坐标.
20.如图,排球运动员站在点O处练习发球,将球从O点正上方的A处发出,把球看成点,其运行的高度与运行的水平距离满足关系式.已知球网与O点的水平距离为,高度为,球场的边界距O点的水平距离为.
(1)当时,求y与x的关系式(不要求写出自变量x的取值范围);
(2)当时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
21.如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)该运动员身高1.7米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?.
22.用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种)
设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
(1)在图①中,如果不锈钢材料总长度为 12 米,当x为多少时,矩形框架ABCD的面积为 3 平方米?
(2)在图②中,如果不锈钢材料总长度为 12 米,当x为多少时,矩形架ABCD的面积S最大?最大面积是多少?
(3)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,那么当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
23.如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC= .
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】C
【解析】【解答】解:选项A中, 不是二次函数,故选项A错误;
选项B中, 不是二次函数,故选项B错误;
选项C中, 是二次函数,故选项C正确;
选项D中, 不是二次函数,故选项D错误.
故答案为:C.
【分析】形如“y=ax2+bx+c(a、b、c是常数,且a≠0)”的函数就是二次函数,据此判断.
2.【答案】A
【解析】【解答】解:∵,
∴此函数的顶点坐标为(3,1),
故答案为:A.
【分析】根据二次函数的图象与性质求解即可。
3.【答案】D
【解析】【解答】∵二次函数解析式是
∴对称轴是直线
故答案为:D
【分析】根据二次函数顶点式的性质直接写出对称轴即可。
4.【答案】B
【解析】【解答】由抛物线平移的规律,可得将抛物线y=2x2向下平移2个单位后所得到的抛物线为,
故答案为:B.
【分析】利用抛物线的平移规律即可写出表达式。
5.【答案】B
【解析】【解答】解:根据题意的得:
解得:
∴m=-2,
故答案为:B.
【分析】根据二次函数的定义,令x的指数为2,系数不为0,列出方程与不等式解答即可.
6.【答案】C
【解析】【解答】解:A、由一次函数y=ax-a的图象可得:a>0,此时一次函数y=ax-a的图象与y轴相交于负半轴,二次函数y=ax2-2x+1的图象开口向上,对称轴x=->0,故选项A错误;
B、由一次函数y=ax-a的图象可得:a<0,此时二次函数y=ax2-2x+1的图象开口向下,故选项B错误;
C、由一次函数y=ax-a的图象可得:a<0,此时二次函数y=ax2-2x+1的图象开口向下,对称轴x=-<0,故选项C正确;
D、由一次函数y=ax-a的图象可得:a<0,此时二次函数y=ax2-2x+1的图象开口向下,对称轴x=-<0,故选项D错误.
故答案为:C.
【分析】 先根据一次函数的图象判断a的符号,再判断二次函数图象与实际是否相符,然后判断正误,即可得出答案.
7.【答案】C
【解析】【分析】采用逐一排除的方法.先根据对称轴为直线x=2排除B、D,再将点(0,1)代入A、C两个抛物线解析式检验即可.
【解答】∵抛物线对称轴为直线x=2,
∴可排除B、D选项,
将点(0,1)代入A中,得(x-2)2+1=(0-2)2+1=5,故A选项错误,
代入C中,得(x-2)2-3=(0-2)2-3=1,故C选项正确.
故选:C.
【点评】本题考查了二次函数的性质.关键是根据对称轴,点的坐标与抛物线解析式的关系,逐一排除.
8.【答案】B
【解析】【解答】因为
二次函数y=ax2+bx+c(a≠0 )与x轴交于点(-2,0)、(6,0),故方程
ax2+bx+c=0的两个实数根为-2和6。
故答案为:B。
【分析】抛物线开口向下故a<0,对称轴在y轴右侧,a、b异号,与y轴交于点(0,4),故c=4,abc<0;抛物线y=ax2+bx+c(a≠0 )与x轴交点的横坐标就是方程ax2+bx+c=0的解;当x=-1时,抛物线上点在x轴上方,故a-b+c>0,当y=4时,根据函数的对称性,x的取值为0或4。
9.【答案】A
【解析】【解答】解:∵y=x2﹣6x+k,
∴图象的开口向上,对称轴是直线x= =3,
C(3+ ,y3)关于直线x=3的对称点是(3- ,y3),
∵ 1<1<3- ,
∴y1>y2>y3,
故答案为:A.
【分析】先求出二次函数的队曾在,再求出点A、B、C到对称轴的距离,再根据二次函数增减性判断即可。
10.【答案】B
【解析】【分析】由二次函数的解析式可知,当x=1时,所对应的函数值y=t=a+b+1.把点(-1,0)代入y=ax2+bx+1,a-b+1=0,然后根据顶点在第一象限,可以画出草图并判断出a与b的符号,进而求出t=a+b+1的变化范围.
【解答】∵二次函数y=ax2+bx+1的顶点在第一象限,
且经过点(-1,0),
∴易得:a-b+1=0,a<0,b>0,
由a=b-1<0得到b<1,结合上面b>0,所以0<b<1①,
由b=a+1>0得到a>-1,结合上面a<0,所以-1<a<0②,
∴由①+②得:-1<a+b<1,
在不等式两边同时加1得0<a+b+1<2,
∵a+b+1=t代入得0<t<2,
∴0<t<2.
故选:B
【点评】此题主要考查了二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特殊点的关系,也要掌握在图象上表示一元二次方程ax2+bx+c=0的解的方法.同时注意特殊点的运用.
11.【答案】
【解析】【解答】解:A(-1,3),B(2,3)是抛物线y=ax2+bx+c(a≠0)上两点,
抛物线的对称轴为
故答案为: .
【分析】根据抛物线的对称性进行解答即可.
12.【答案】
【解析】【解答】解:由图象可知:二次函数y=ax2+bx+c的顶点坐标为(1,5),
∴ =5,即b2-4ac=-20a,
∵ax2+bx+c=k有两个不相等的实数根,
∴方程ax2+bx+c-k=0的判别式△>0,即b2-4a(c-k)=b2-4ac+4ak=-20a+4ak=-4a(5-k)>0
∵抛物线开口向下
∴a<0
∴5-k>0
∴k<5.
故答案为:k<5.
【分析】根据二次函数的一般形式的顶点坐标为(,),可得b2-4ac=-20a,再根据一元二次方程的根的判别式可得,结合抛物线开口向下确定a的符号,即可求解。
13.【答案】大;(0,15)
【解析】【解答】解:∵ 抛物线y=-x2+15
a=-1<0
∴抛物线开口向下,则抛物线y=-x2+15有最大值,顶点坐标为:(0,15)
故答案为:大;(0,15)
【分析】根据函数解析式,由a<0可知抛物线开口向下,抛物线有最高点,则函数有最大值;再求出顶点坐标。
14.【答案】b≤-4
【解析】【解答】解:将点 代入 得:
,
整理得: ,
,
,解得 ,
则抛物线的解析式为 ,
当 时, ,即 ,
当 时, ,即 ,
点 为抛物线上A,B两点之间(包含A,B两点)的一个动点,且 ,
,
解得 ,
故答案为:b≤-4.
【分析】先将点代入函数,整理得到a=1, 则抛物线为y=x2+bx 3,所以抛物线开口向上,接着求出A、B的坐标,最后根据进而即可求出答案.
15.【答案】解:设售价为x元,获得的利润为y元,则销售个数为500-20(x-50),
由题意得,
y=(x-40)×(500-20x+1000)
=-20(x-40)(x-75)
=-20(x2-115x+3000)
=-20(x-57.5)2-60000+66125
=-20(x-57.5)2+6125
答:当x=57.5元时得到最大利益6125元.
【解析】【分析】设售价为x元,获得的利润为y元,根据题意列出函数解析式y=(x-40)×(500-20x+1000)=-20(x-57.5)2+6125,再利用二次函数的性质求解即可。
16.【答案】解:由图可知,图象过(-1, 0)、(2, 0)、(0, -2)三点,
设这个二次函数解析式为y=ax2 +bx+c(a≠0),把以上三点代入解析式得:
解得:
∴这个二次函数解析式为y=x2-x+2;
【解析】【分析】观察图象得出抛物线经过(-1, 0)、(2, 0)、(0, 2)三点, 设这个二次函数解析式为y=ax2+bx+c代入抛物线的解析式得出关于a,b,c的方程组,解方程组得出a,b,c的值,即可得出答案.
17.【答案】解:如图,
y2的图象由y1=2x2的图象向右平移2个单位得到;
y3的图象由y1=2x2的图象向左平移2个单位得到.
【解析】【分析】由图像可知:向右平移2个单位长度可得抛物线;向左平移2个单位长度可得抛物线。
18.【答案】解:(1)由抛物线经过A(-1,0),B(4,0),
设抛物线的解析式为:y=a(x+1)(x-4),
将C(0,-4)代入上式中,得-4a=-4,a=1.
∴y=(x+1)(x-4)=x2-3x-4.
(2)∵A(-1,0),B(4,0),C(0,-4).
∴OB=OC=4,OA=1
∴∠OBC=45°,∴∠AMC=90°
∴AM2+MC2=OA2+OC2=12+42=17
∴AM2=CM2=,
∴S阴影=.
(3)∠OBC=45°,PQ⊥x轴;
∴BP=PQ=k,
∴S=k (4-k)=-k2+2k.
∴当k=2时,S最大值=2.
【解析】【分析】
(1)已知了A、B、C三点坐标可用待定系数法求出抛物线的解析式.
(2)要求扇形的面积需要知道半径的长和扇形的圆心角的度数,先求圆心角∠AMC的度数,由于OB=OC,因此∠ABC=45°,根据圆周角定理可得出∠AMC=90°.再求半径,由于三角形AMC是等腰直角三角形,因此半径的平方等于AC的平方的一半,可在直角三角形OAC中求出AC的平方,据此可根据扇形的面积公式求出扇形的面积.
(3)求三角形CPQ的面积可以PQ为底,以OP为高,已知了PQ=k,在等腰直角三角形BPQ中,BP=PQ=k,也就能表示长OP的长,据此可求出S与k的函数关系,根据函数的性质即可求出S的最大值.
19.【答案】(1)由y=-(m+2) (m为常数),y是x的一次函数,得 解得m=± ,当m=± 时,y是x的一次函数.
(2)由y=-(m+2) (m为常数),y是x的二次函数,得 解得m=2,m=-2(错误的要舍去),当m=2时,y是x的二次函数,当y=-8时,-8=-4x2,解得x=± ,故纵坐标为-8的点的坐标是(± ,-8).
【解析】【分析】(1)根据形如y=kx(,k是常数)是一次函数,可得出一次函数;
(2)根据根据形如(是常数,)是二次函数,可得答案,根据函数值,得出自变量的值,即可得出符合条件的点。
20.【答案】(1)解:由图象可知:点A的坐标为
将点和代入解析式中,得
,解得:
∴y与x的关系式为.
(2)解:球能越过球网,球不会出界,理由如下
将代入中,得
,
∴球能越过球网;
将代入中,得
,
∴该抛物线与x轴的右交点必在(18,0)的左侧,
∴球不会出界,
综上:球能越过球网,球不会出界.
(3)解:将点代入解析式中,得:
解得:
∴抛物线的解析式为
若球一定能越过球网,则当时, ;
∴,解得:
若不出边界,即抛物线与x轴的右交点在的左侧或重合,即当时,;
∴,解得
综上:若球一定能越过球网,又不出边界,h的取值范围为.
【解析】【分析】(1)由题意得A(0,2),将点A(0,2)及h=2.8分别代入y=a(x-6)2+h可求出a的值,从而得出y关于x的函数解析式;
(2)将x=9代入(1)所求的函数解析式算出对应的函数值,再将该值与2.45比大小即可判断得出球是否过网;将x=9代入(1)所求的函数解析式算出对应的函数值,再将该值与0比大小即可判断得出球是否出界;
(3)将点A(0,2)代入y=a(x-6)2+h可表示出a的值为 ,得抛物线的解析式为, 若球一定能越过球网,则当x=9时, y>2.45,据此建立不等式求解得出h的取值范围, 若不出边界,即抛物线与x轴的右交点在(18,0)的左侧或重合,即当x=18时,y≤0,据此建立不等式,求解可得h的取值范围,综上即可得出答案.
21.【答案】(1)解:抛物线的顶点坐标为(0,3.5),
∴设抛物线的表达式为y=ax2+3.5,
由图可知函数图象过点(1.5,3.05),
∴2.25a+3.5=3.05,
解得:a=-0.2,
∴抛物线的表达式为y= - 0.2x2+3.5;
(2)解:设球出手时,他跳离地面的高度为hm,则球出手时,球的高度为(h+1.7+0.25)m,
∵(1)中求得y= - 0.2x2+3.5,
∴ ,
解得:h=0.3,
答:球出手时,他跳离地面的高度为0.3m.
【解析】【分析】(1)设抛物线的表达式为y=ax2+3.5,依题意可知函数图象经过点(1.5,3.05),代入可得a的值;(2)设球出手时,他跳离地面的高度为hm,则可得 ,解方程求出h即可.
22.【答案】(1)解: AD= ,
由题意得: ,
,
∴ ,
答:当 或3米时,矩形框架ABCD的面积为3平方米;
(2)解: ,
,
,
当 时,
4 ,
答:当 时,矩形架ABCD的面积S最大,最大面积是3平方米;
(3)解: ,
,
,
当 时
.
答:当 时,矩形ABCD的面积S最大,最大面积是 平方米.
【解析】【分析】(1)由题意可得3AD+3AB=12,从而可得出AD的表达式;根据矩形的面积=长×宽,可得出方程;(2)由题意可得3AD+4AB=12,从而可得出AD的表达式;根据矩形的面积=长×宽,可得出S与x的函数关系式;(3)由题意可得3AD+nAB=a,从而可得出AD的表达式,根据矩形的面积=长×宽,可得出S与x的函数关系式,利用配方法可求出S的最大值.
23.【答案】(1)解:∵C(0,3),
∴OC=3,
∵tan∠OAC= ,
∴OA=4,
∴A(﹣4,0).
把A(﹣4,0)、C(0,3)代入y=ax2+2ax+c中,
得 ,解得: ,
∴抛物线的解析式为y=﹣ x2﹣ x+3
(2)解:设直线AC的解析式为y=kx+b,
把A(﹣4,0)、C(0,3)代入y=kx+b中,
得: ,解得: ,
∴直线AC的解析式为y= x+3.
设N(x,0)(﹣4<x<0),则H(x, x+3),P(x,﹣ x2﹣ x+3),
∴PH=﹣ x2﹣ x+3﹣( x+3)=﹣ x2﹣ x=﹣ (x+2)2+ ,
∵﹣ <0,
∴PH有最大值,
当x=﹣2时,PH取最大值,最大值为
(3)解:过点M作MK⊥y轴于点K,交对称轴于点G,则∠MGE=∠MKC=90°,
∴∠MEG+∠EMG=90°,
∵四边形CMEF是正方形,
∴EM=MC,∠MEC=90°,
∴∠EMG+∠CMK=90°,
∴∠MEG=∠CMK.
在△MCK和△MEG中, ,
∴△MCK≌△MEG(AAS),
∴MG=CK.
由抛物线的对称轴为x=﹣1,设M(x,﹣ x2﹣ x+3),则G(﹣1,﹣ x2﹣ x+3),K(0,﹣ x2﹣ x+3),
∴MG=|x+1|,CK=|﹣ x2﹣ x+3﹣3|=|﹣ x2﹣ x|=| x2+ x|,
∴|x+1|=| x2+ x|,
∴ x2+ x=±(x+1),
解得:x1=﹣4,x2=﹣ ,x3=﹣ ,x4=2,
代入抛物线解析式得:y1=0,y2= ,y3= ,y4=0,
∴点M的坐标是(﹣4,0),(﹣ , ),(﹣ , )或(2,0).
【解析】【分析】(1)由点C的坐标以及tan∠OAC= 可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;(2)设直线AC的解析式为y=kx+b,由点A、C的解析式利用待定系数法即可求出直线AC的解析式,设N(x,0)(﹣4<x<0),可找出H、P的坐标,由此即可得出PH关于x的解析式,利用配方法即二次函数的性质即可解决最值问题;(3)过点M作MK⊥y轴于点K,交对称轴于点G,根据角的计算依据正方形的性质即可得出△MCK≌△MEG(AAS),进而得出MG=CK.设出点M的坐标利用正方形的性质即可得出点G、K的坐标,由正方形的性质即可得出关于x的含绝对值符号的一元二次方程,解方程即可求出x值,将其代入抛物线解析式中即可求出点M的坐标.本题考查了待定系数法求函数解析式、二次函数的性质、正方形的性质以及全等三角形的判定与性质,解题的关键是:(1)利用待定系数法求出抛物线解析式;(2)根据二次函数的性质解决最值问题;(3)根据正方形的性质得出关于x的含绝对值符号的一元二次方程.本题属于中档题,难度不大,解决该题型题目时,根据正方形的性质找出关于x的含绝对值符号的一元二次方程,解方程求出点的横坐标是关键.
1 / 1
