华东师大版八年级数学上册综合复习题(含解析)
文档属性
| 名称 | 华东师大版八年级数学上册综合复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 513.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 14:53:13 | ||
图片预览



文档简介
华东师大版八年级数学上册综合复习题
一、单选题
1.计算的结果为( )
A. B. C. D.
2.下列各式从左到右的变形,属于因式分解的是( )
A. B.
C. D.
3.如图,△ABC≌△CDA,若AB=3,BC=4,则四边形ABCD的周长是( )
A.14 B.11 C.16 D.12
4.下列句子中,属于命题的是( )
①三角形的内角和等于180度;②对顶角相等;③过一点作已知直线的垂线;④两点确定一条直线.
A.①④ B.①②④ C.①②③ D.②③
5.如图,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )
A. B.
C. D.
6.下列命题:①内错角相等;②数轴上的点与实数是一一对应的;④过一点有且只有一条直线和这条直线平行;④从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离;⑤若直线,,则bc.其中真命题的个数为( )
A.1 B.2 C.3 D.4
7.估计的值在( )
A.3.3和3.4之间 B.3.4和3.5之间
C.3.5和3.6之间 D.3.6和3.7之间
8.一个底面是长方形的小塑料盒,长为40cm,宽为30cm,在小塑料盒底面放一根木棒,那么这根木棒最长(不计木棒粗细)可以是( )
A.30cm B.40cm C.50cm D.
9.下列说法:①0是绝对值最小的有理数;②乘以任何数仍得这个数;③数轴上原点两侧的数互为相反数;④一个数的平方是正数,则这个数的立方也是正数;⑤一对相反数的平方也互为相反数.其中不正确的说法有( )
A.1个 B.2个 C.3个 D.4个
10.下列各式成立的是( )
A. B.
C. D.以上各式都不成立
二、填空题
11.分解因式:m2n-2mn+n= .
12.若x2+mx+n=(x-2)(x-1)则mn= .
13.如图, , 、 的平分线交于点O, 于E,且 cm,则直线 与 的距离为 cm.
14.等腰三角形的周长为14,其一边长为4,那么,它的底边为 .
15.等腰△ABC中,∠A的外角等于130°,那么∠B= .
16.如图所示,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点M,若CM=5,则CE2+CF2等于
17.如图,从电线杆高于地面6m的C处,向地面拉一条10m长的缆绳AC,那么固定点A到电线杆底部B的距离为 m.
18. ,则 的值为
三、解答题
19.已知x-2的算术平方根是2,2x+y-1的立方根是3,求y-2x的平方根.
20.如图,已知点B,C,F,E在同一直线上,∠1=∠2,BF=CE,AB∥DE.
求证:△ABC≌△DEF.
21.幂的运算:
(1)计算:(﹣a3)2+(﹣a2)3
(2)计算:
(3)
(4)我们已经学习了四个关于幂的运算法则:①am an=am+n;②(am)n=amn;③(ab)m=ambm;④am÷an=am﹣n,下面是小明计算的过程(a3 a2)3=(a3+2)3=(a5)3=a15,他用到的公式有 (填序号)
22.如图.AB=AD,∠ABC=∠ADC,求证:BC=DC.
23.如图,已知∠EPM=∠FQM.∠AEP=∠CFQ.试说明AB∥CD的理由.
24.如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13,求这个四边形ABCD的面积
25.已知2a-1的算术平方根为3,3a+b-1的算术平方根为4,求a+2b的平方根.
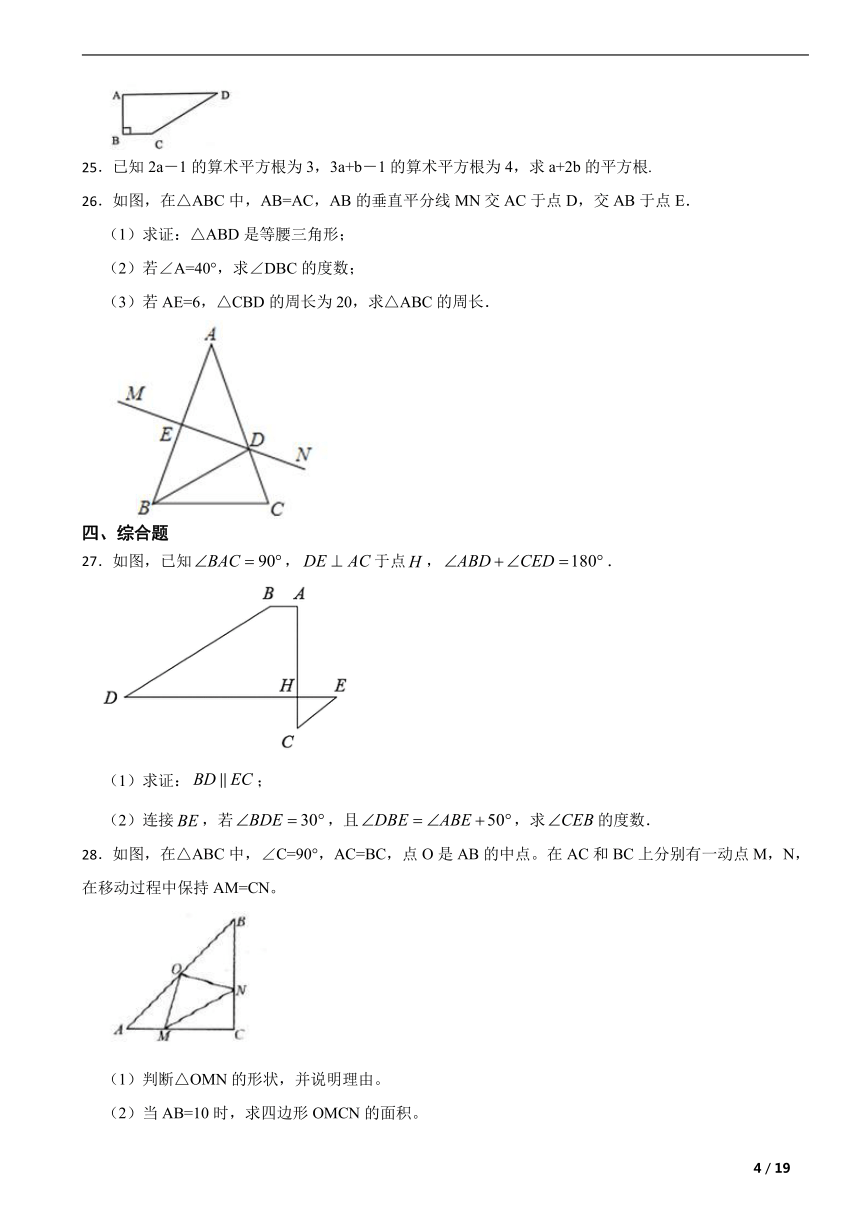
26.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
四、综合题
27.如图,已知,于点,.
(1)求证:;
(2)连接,若,且,求的度数.
28.如图,在△ABC中,∠C=90°,AC=BC,点O是AB的中点。在AC和BC上分别有一动点M,N,在移动过程中保持AM=CN。
(1)判断△OMN的形状,并说明理由。
(2)当AB=10时,求四边形OMCN的面积。
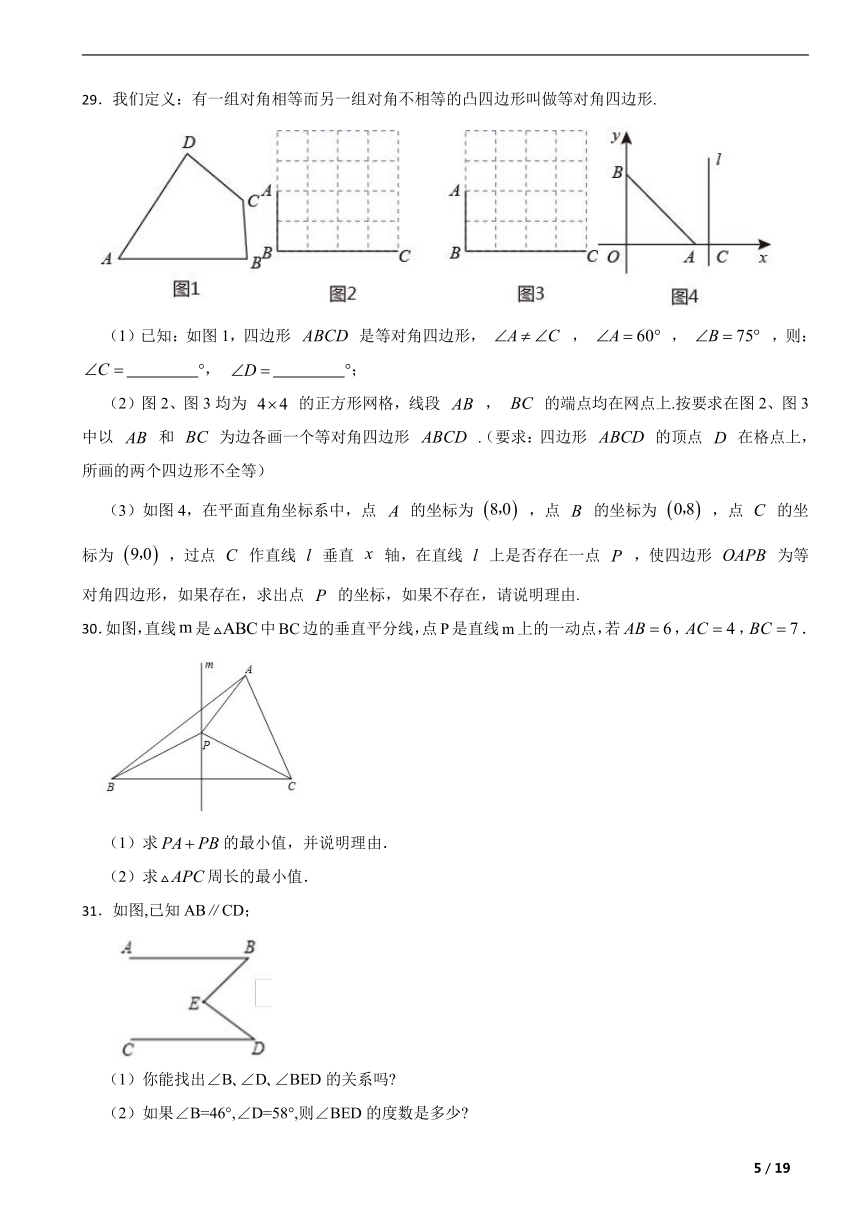
29.我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.
(1)已知:如图1,四边形 是等对角四边形, , , ,则: °, °;
(2)图2、图3均为 的正方形网格,线段 , 的端点均在网点上.按要求在图2、图3中以 和 为边各画一个等对角四边形 .(要求:四边形 的顶点 在格点上,所画的两个四边形不全等)
(3)如图4,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,点 的坐标为 ,过点 作直线 垂直 轴,在直线 上是否存在一点 ,使四边形 为等对角四边形,如果存在,求出点 的坐标,如果不存在,请说明理由.
30.如图,直线是中BC边的垂直平分线,点P是直线m上的一动点,若,,.
(1)求的最小值,并说明理由.
(2)求周长的最小值.
31.如图,已知AB∥CD;
(1)你能找出∠B ∠D ∠BED的关系吗
(2)如果∠B=46°,∠D=58°,则∠BED的度数是多少
32.(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合,研究数轴我们发现了许多重要的规律:数轴上 点、 点表示的数为 、 ,则 , 两点之间的距离 ,若 ,则可简化为 ;线段 的中点 表示的数为 .
(问题情境)
已知数轴上有 , 两点,分别表示的数为 ,8,点 以每秒3个单位的速度沿数轴向右匀速运动,点 以每秒2个单位向左匀速运动,设运动时间为 秒( ).
(综合运用)
(1)运动开始前, , 两点的距离为 ;线段 的中点 所表示的数 .
(2)点 运动 秒后所在位置的点表示的数为 ;点 运动 秒后所在位置的点表示的数为 ;(用含 的式子表示)
(3)它们按上述方式运动, , 两点经过多少秒会相距4个单位长度?
(4)若 , 按上述方式继续运动下去,线段 的中点 能否与原点重合?若能,求出运动时间,并直接写出中点 的运动方向和运动速度;若不能,请说明理由.(当 , 两点重合,则中点 也与 , 两点重合).
答案解析部分
1.【答案】C
【解析】【解答】解:
.
故答案为:C.
【分析】根据幂的乘方法则可得。
2.【答案】B
【解析】【解答】解:A、原式是整式的乘法,不是因式分解,故本选项不符合题意;
B、原式符合因式分解的定义,是因式分解,故本选项符合题意;
C、原式的右边不是几个整式积的形式,不是因式分解,故本选项不符合题意;
D、x2-2x-1≠(x-1)2,故本选项不符合题意.
故答案为:B.
【分析】因式分解是把多项式写成几个整式积的形式的恒等变形,据此对各选项分析判断后利用排除法求解.
3.【答案】A
【解析】【解答】∵△ABC≌△CDA,
∴AB=CD,AD=BC,
∵AB=3,BC=4,
∴四边形ABCD的周长AB+BC+CD+DA=3+3+4+4=14,
故答案为:A.
【分析】根据全等三角形的性质得到AB=CD,AD=BC,进而求出四边形ABCD的周长.
4.【答案】B
【解析】【解答】解: ①三角形的内角和等于180°,是三角形内角和定理,是命题;
②对顶角相等,是对顶角的性质,是命题;
③过一点作已知直线的垂线,是作图,不是命题;
④两点确定一条直线,是直线的性质,是命题,
综上所述,属于命题是①②④.
故答案为:B.
【分析】对一件事情进行判断的语句叫命题,据此分别对每一项是否是命题进行判断即可.
5.【答案】A
【解析】【解答】解:由题意可得:a2 b2=(a b)(a+b).
故答案为:A.
【分析】由两图阴影部分的面积相等可得:a2 b2=(a b)(a+b)。
6.【答案】A
【解析】【解答】解:①两直线平行,内错角相等,故原命题为假命题;
数轴上的点与实数是一一对应的,为真命题;
经过直线外一点,有且只有一条直线与这条直线平行,故原命题为假命题;
从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离,故原命题为假命题;
在同一平面内,若直线,,则bc,故原命题为假命题;
故真命题为:.
故答案为:A.
【分析】根据真命题的定义逐项判断即可。
7.【答案】C
【解析】【解答】解:∵, , , ,
∴
∴
故答案为C.
【分析】根据 , , 可得 ,因此 ,从而得解。
8.【答案】C
【解析】【解答】解:∵长方形塑料盒的长为40,宽为30,
∴木棒最长为=50.
故答案为:C.
【分析】由题意可得:木棒的最大长度为底面长方形的对角线长,然后利用勾股定理计算即可.
9.【答案】D
【解析】【解答】①∵0是绝对值最小的有理数,∴①正确;
②∵乘以任何数得这个数的相反数,∴②不正确;
③∵数轴上原点两侧且与原点距离相等的数互为相反数,∴③不正确;
④∵负数的平方是正数,则这个数的立方也是负数,∴④不正确;
⑤∵一对相反数的平方应该相等,∴⑤不正确;
综上,不正确的结论是②③④⑤,共有4个,
故答案为:D.
【分析】利用绝对值的性质,相反数的性质及假命题的定义逐项判断即可.
10.【答案】C
【解析】【解答】解:A中 ,错误,故不符合题意;
B中 ,错误,故不符合题意;
C中 ,正确,故符合题意;
故答案为:C.
【分析】根据完全平方公式的展开式是一个三项式可判断A、B;根据平方差公式:两个数的平方差,等于这两个数的和乘以这两个数的差,可判断C.
11.【答案】n(m-1)2
【解析】【解答】解:m2n-2mn+n=n(m2-2m+1)=n(m-1)2.
【分析】先提公因式,然后运用完全平方公式进行因式分解。
12.【答案】9
【解析】【解答】解:∵x2+mx+n
=(x-2)(x-1)
=x2-3x+2
∴m=-3,n=2
∴mn=(-3)2=9
故答案为:9.
【分析】利用多项式乘多项式的计算方法可得x2-3x+2,再利用待定系数法可得m=-3,n=2,最后求出mn的值即可。
13.【答案】6
【解析】【解答】解:如图,过O作 交CD于Q,交 于H,
平分
平分
直线 与 的距离为
故答案为:
【分析】过O作 交CD于Q,交 于H,由 平分 得出由 平分 得出由此得出结论。
14.【答案】4或6
【解析】【解答】解:当腰是4时,则另两边是4,6,且4+4>6,6-4<4,满足三边关系定理,
当底边是4时,另两边长是5,5,5+4>5,5-4<5,满足三边关系定理,
∴该等腰三角形的底边为4或6,
故答案为:4或6.
【分析】利用等腰三角形的性质及三角形三边的关系求解即可。
15.【答案】65°或80°或50°.
【解析】【解答】解:(1)当∠A为顶角时,∠A=50°,则 ∠B一定为底角,∠B=65°;
(2)当∠A为底角时,∠A=50°,∠B为底角的话,∠B=50°;
(3)当∠A为底角时,∠A=50°,∠B为顶角的话,∠B=80°;
故答案为:65°或80°或50°.
【分析】根据题意得∠A=50°,再分∠A为顶角和底角,根据等腰三角形的性质和三角形的内角和定理即可求得.
16.【答案】100
【解析】【解答】∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=∠BCE=∠ACB,∠MCF=∠DCF=∠ACD,
∴∠ECF=(∠ACB+∠ACD)=90°,
∵EF∥BC ,
∴∠MEC=∠BCE,∠F=∠FCD,
∴∠MEC=∠MCE,∠MCF=∠F,
∴ME=CM=MF=5,即EF=10,
在Rt△ECF中,CE2+CF2=EF2=100.
【分析】利用角平分线的定义先推出∠ECF=90°,再根据平行线的性质及角平分线的定义可得∠MEC=∠MCE,∠MCF=∠F,从而得出ME=CM=MF=5,即EF=10,利用勾股定理可得CE2+
CF2=EF2,即可求出结论.
17.【答案】8
【解析】【解答】解:在Rt△ABC中,由勾股定理得:
AB===8(m),
即固定点A到电线杆底部B的距离是8m,
故答案为:8.
【分析】利用勾股定理先求出AB=8,再求解即可。
18.【答案】7
【解析】【解答】∵
∴
∴ ,即 =7.
【分析】将已知等式两边除以a变形求值即可.
19.【答案】解:∵x-2的算术平方根是2 ,
∴x-2=4,
x=6,
2x+y-1的立方根是3,
把x=6代入得
12+y-1=27,
y=16,
∴y-2x=16-2×6=4
∴y-2x的平方根为±2.
【解析】【分析】由算术平方根与立方根的含义列方程组,解方程组即可得到答案.
20.【答案】解:∵BF=CE,
∴BF-FC=CE-CF,即BC=EF,
∵AB∥DE,
∴∠E=∠B,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS).
【解析】【分析】根据等式的性质,由 BF=CE, 得出 BC=EF, 根据二直线平行,内错角相等得出 ∠E=∠B, 从而利用AAS判断出 △ABC≌△DEF .
21.【答案】(1)解:原式=a6﹣a6
=0
(2)解:原式=﹣4+4﹣1
=﹣1
(3)解:原式=[(﹣3)×(﹣ )]100×(﹣ )
=1100×(﹣ )
=﹣
(4)①②
【解析】【解答】(4)小明计算的过程(a3 a2)3=(a3+2)3=(a5)3=a15,他用到的公式有①②,
故答案为:①②.
【分析】(1)先算乘方,再合并同类项即可;(2)先根据负整数指数幂,零指数幂进行计算,再求出即可;(3)根据积的乘方进行计算即可;(4)根据算式得出答案即可.
22.【答案】证明:连接BD,
∵AB=AD,
∴∠ABD=∠ADB.
∵∠ABC=∠ADC,
∴∠CBD=∠CDB.
∴BC=DC.
【解析】【分析】连接BD,由等边对等角得到∠ABD=∠ADB,再由等量减去等量还是等量,得到∠CBD=∠CDB,由等角对等边得到BC=CD.
23.【答案】解:∵ ∠EPM=∠FQM ,
∴PE∥FQ,
∴ ∠PEM=∠QFM ,
又∵ ∠AEP=∠CFQ ,
∴ ∠PEM-∠AEP=∠QFM-∠CFQ ,
即∠AEM=∠CFM,
∴AB∥CD.
【解析】【分析】由同位角相等,两直线平行,得PE∥FQ,由两直线平行,同位角相等,得∠PEM=∠QFM ,结合∠AEP=∠CFQ ,根据等式的性质可以推出∠AEM=∠CFM,最后再根据同位角相等,两直线平行,得出结论.
24.【答案】解:
解:连接AC
在△ABC中, ∠B=90°,AB=4,BC=3,
所以AC=
在△ACD中, CD=12,AD=13, AC=5,
所以AC2+CD2=AD2
所以∠ACD=90°
【解析】
【分析】本题考查勾股定理及勾股定理的逆定理,先利用勾股定理计算出AC的长度,然后利用勾股定理逆定理判定△ACD为直角三角形,再把四边形ABCD的面积拆分为两个直角三角形的面积计算即可。
25.【答案】解:由题意得2a-1=9,3a+b-1=16,
解得:a=5,b=2,
则a+2b=9,
∴a+2b的平方根是 .
【解析】【分析】利用平方根及算术平方根的定义列出方程,得到a与b的值,确定出a+2b的值,即可求出平方根.
26.【答案】解:(1)证明:∵AB的垂直平分线MN交AC于点D,∴DB=DA,∴△ABD是等腰三角形;(2)∵△ABD是等腰三角形,∠A=40°,∴∠ABD=∠A=40°,∠ABC=∠C=(180°﹣40°)÷2=70°∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°;(3)∵AB的垂直平分线MN交AC于点D,AE=6,∴AB=2AE=12,∵△CBD的周长为20,∴AC+BC=20,∴△ABC的周长=AB+AC+BC=12+20=32.
【解析】【分析】(1)根据线段的垂直平分线到线段两端点的距离相等即可得证;
(2)首先利用三角形内角和求得∠ABC的度数,然后减去∠ABD的度数即可得到答案;
(3)将△ABC的周长转化为AB+AC+BC的长即可求得.
27.【答案】(1)证明:,
,
,
,
,
,
,
,
.
(2)解:如图,连接,
设,
,
,
,
由(1)已得:,
,
,
解得,
即,
由(1)已证:,
.
【解析】【分析】(1)根据题意得出,根据平行线的性质推出,即可得出结论;
(2)连接,根据平行线的性质求出答案即可。
28.【答案】(1)△OMN 是等腰直角三角形.理由如下:连接 OC.
∵AC=BC,点 O 是 AB 的中点,
∴OC⊥AB,∠1=∠2
∵∠ACB=90°,
∴∠1=∠2=45°. ∴∠A=45°.
∴∠A=∠1,∠A=∠2.
∴OA=OC.
∵AM=CN,
∴△AMO≌△CNO(SAS)
∴OM=ON,∠3=∠4.
∴∠MON=∠AOC=90°.
∴△OMN 是等腰直角三角形.
(2)由(1),△AMO≌△CNO.
∴S 四 OMCN=S△OAC.
由(1)OA=OC= 12 AB=5.
∴S 四 OMCN= 12 OA·OC= 252 。
【解析】【分析】(1)连接OC,根据等腰三角形的三线合一定理即可得到∠1=∠2,继而证明△AMO≌△CNO,即可证明三角形OMN为等腰直角三角形。
(2)根据(1)中三角形全等的性质,进行面积的计算即可。
29.【答案】(1)150;75
(2)解:如图所示:
(3)解:①当 时,可以得到点 在 的平分线上,
∴ ,
∴ ,
∴点 的坐标为 ;
② 时,过 作 于点 ,
设点 的坐标为 ,则
∴
∴
∴
∴
∴点 的坐标为 .
【解析】【解答】(1)解:∵四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=60°,∠B=75°,
∴∠D=∠B=75°,
∴∠C=360°-75°-75°-60°=150°;
故答案为150,75.
【分析】(1)由四边形ABCD是“等对角四边形”可得∠D=∠B=75°,然后根据四边形内角和为360°进行求解;
(2)根据一组对角相等而另一组对角不相等进行作图;
(3)①当∠OBP=∠OAP时,可以得到点P在△AOB的平分线上,进而推出OC=PC,据此可得点P的坐标;②当∠AOB=∠APB=90° 时,过B作BH⊥l于点H,设P(9,m),则HP=8-m,根据BH2+PH2+PC2+AC2=AB2=OA2+OB2就可得到m的值,进而得到点P的坐标.
30.【答案】(1)解:当A,B,P三点共线时,PA+PB最小短
;
原因:两点之间,线段最短.
(2)解:∵直线m是BC的垂直平分线,点P在m上,
∴点C关于直线m的对称点是点B,
则 ,
∵ ,
∵ ,
要使 周长最小,
即 最小,
当点P是直线m与AB的交点时, 最小,
即 ,此时 .
【解析】【分析】(1)利用两点之间线段最短,可知当当A,B,P三点共线时,PA+PB最小.
(2)利用垂直平分线上的点到线段两端点的距离相等,可证得BP=PC;利用△APC的周长为AP+AC+PC,而AC是定值,要使△APC的周长最小,可知AP+PC的值最小,由此可知当点P是直线m与AB的交点时,可知PA+PB最小,即可求出△APC周长的最小值.
31.【答案】(1)∠BED=∠B+∠D,理由如下
过点E作EF∥AB
∵AB∥CD
∴EF∥AB∥CD
∴∠B=∠BEF,∠D=∠DEF
∴∠BED=∠BEF+∠DEF=∠B+∠D
(2)∵∠BED=∠B+∠D,∠B=46°,∠D=58°,
∴∠BED=46°+58°=104°
【解析】【分析】(1)过点E作EF∥AB,根据平行于同一条直线的两直线平行可得EF∥AB∥CD,然后根据平行线的性质可得∠B=∠BEF,∠D=∠DEF,然后根据角的关系和等量代换即可得出结论;(2)根据(1)的结论代入各角的度数即可求出结论.
32.【答案】(1)18;
(2);
(3)解:设它们按上述方式运动, 、 两点经过 秒会相距4个单位长度,
当点 在点 左侧时,
依题意列式,得 ,解得 ;
当点 在点 右侧时,
,解得 ,
答:它们按上述方式运动, 、 两点经过2.8秒或4.4秒会相距4个单位长度.
(4)解:能.
设 、 按上述方式继续运动 秒线段的中点 能与原点重合,
根据题意列方程,可得 ,解得 .
运动开始前 点的位置是 ,运动2秒后到达原点,
由此得 点的运动方向向右,其速度为: 个单位长度.
答:运动时间为2秒,中点 点的运动方向向右,其运动速度为每秒 个单位长度.
【解析】【解答】解:(1) 、 两点的距离为: ;线段 的中点 所表示的数为 .
故答案为:18; ;
( 2 )由题意可得点 运动 秒后所在位置的点表示的数为 ;点 运动 秒后所在位置的点表示的数为 ;
故答案为: ; ;
【分析】(1)根据数轴的基本概念,由题意可得A与B两点之间的距离以及线段AB的中点表示的数.(2)由题意可得,点A运动t秒后所在位置的点表示的数等于运动开始前点A表示的数加上点A运动的路程,即-10+3t,点B运动t秒后所在位置的点表示的数等于运动开始前点B表示的数减去点B运动的路程,即8-2t.
(3)设它们按上述方式运动,A、B两点经过t秒会相遇,根据题意列方程求解即可.
(4)设A,B按上述方式继续运动秒线段的中点能与原点重合,根据题意列方程,解得k值,再由运动开始前点M的位置及k秒后所到的位置得出点M的运动方向向右及速度.
1 / 1
一、单选题
1.计算的结果为( )
A. B. C. D.
2.下列各式从左到右的变形,属于因式分解的是( )
A. B.
C. D.
3.如图,△ABC≌△CDA,若AB=3,BC=4,则四边形ABCD的周长是( )
A.14 B.11 C.16 D.12
4.下列句子中,属于命题的是( )
①三角形的内角和等于180度;②对顶角相等;③过一点作已知直线的垂线;④两点确定一条直线.
A.①④ B.①②④ C.①②③ D.②③
5.如图,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )
A. B.
C. D.
6.下列命题:①内错角相等;②数轴上的点与实数是一一对应的;④过一点有且只有一条直线和这条直线平行;④从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离;⑤若直线,,则bc.其中真命题的个数为( )
A.1 B.2 C.3 D.4
7.估计的值在( )
A.3.3和3.4之间 B.3.4和3.5之间
C.3.5和3.6之间 D.3.6和3.7之间
8.一个底面是长方形的小塑料盒,长为40cm,宽为30cm,在小塑料盒底面放一根木棒,那么这根木棒最长(不计木棒粗细)可以是( )
A.30cm B.40cm C.50cm D.
9.下列说法:①0是绝对值最小的有理数;②乘以任何数仍得这个数;③数轴上原点两侧的数互为相反数;④一个数的平方是正数,则这个数的立方也是正数;⑤一对相反数的平方也互为相反数.其中不正确的说法有( )
A.1个 B.2个 C.3个 D.4个
10.下列各式成立的是( )
A. B.
C. D.以上各式都不成立
二、填空题
11.分解因式:m2n-2mn+n= .
12.若x2+mx+n=(x-2)(x-1)则mn= .
13.如图, , 、 的平分线交于点O, 于E,且 cm,则直线 与 的距离为 cm.
14.等腰三角形的周长为14,其一边长为4,那么,它的底边为 .
15.等腰△ABC中,∠A的外角等于130°,那么∠B= .
16.如图所示,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点M,若CM=5,则CE2+CF2等于
17.如图,从电线杆高于地面6m的C处,向地面拉一条10m长的缆绳AC,那么固定点A到电线杆底部B的距离为 m.
18. ,则 的值为
三、解答题
19.已知x-2的算术平方根是2,2x+y-1的立方根是3,求y-2x的平方根.
20.如图,已知点B,C,F,E在同一直线上,∠1=∠2,BF=CE,AB∥DE.
求证:△ABC≌△DEF.
21.幂的运算:
(1)计算:(﹣a3)2+(﹣a2)3
(2)计算:
(3)
(4)我们已经学习了四个关于幂的运算法则:①am an=am+n;②(am)n=amn;③(ab)m=ambm;④am÷an=am﹣n,下面是小明计算的过程(a3 a2)3=(a3+2)3=(a5)3=a15,他用到的公式有 (填序号)
22.如图.AB=AD,∠ABC=∠ADC,求证:BC=DC.
23.如图,已知∠EPM=∠FQM.∠AEP=∠CFQ.试说明AB∥CD的理由.
24.如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13,求这个四边形ABCD的面积
25.已知2a-1的算术平方根为3,3a+b-1的算术平方根为4,求a+2b的平方根.
26.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
四、综合题
27.如图,已知,于点,.
(1)求证:;
(2)连接,若,且,求的度数.
28.如图,在△ABC中,∠C=90°,AC=BC,点O是AB的中点。在AC和BC上分别有一动点M,N,在移动过程中保持AM=CN。
(1)判断△OMN的形状,并说明理由。
(2)当AB=10时,求四边形OMCN的面积。
29.我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.
(1)已知:如图1,四边形 是等对角四边形, , , ,则: °, °;
(2)图2、图3均为 的正方形网格,线段 , 的端点均在网点上.按要求在图2、图3中以 和 为边各画一个等对角四边形 .(要求:四边形 的顶点 在格点上,所画的两个四边形不全等)
(3)如图4,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,点 的坐标为 ,过点 作直线 垂直 轴,在直线 上是否存在一点 ,使四边形 为等对角四边形,如果存在,求出点 的坐标,如果不存在,请说明理由.
30.如图,直线是中BC边的垂直平分线,点P是直线m上的一动点,若,,.
(1)求的最小值,并说明理由.
(2)求周长的最小值.
31.如图,已知AB∥CD;
(1)你能找出∠B ∠D ∠BED的关系吗
(2)如果∠B=46°,∠D=58°,则∠BED的度数是多少
32.(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合,研究数轴我们发现了许多重要的规律:数轴上 点、 点表示的数为 、 ,则 , 两点之间的距离 ,若 ,则可简化为 ;线段 的中点 表示的数为 .
(问题情境)
已知数轴上有 , 两点,分别表示的数为 ,8,点 以每秒3个单位的速度沿数轴向右匀速运动,点 以每秒2个单位向左匀速运动,设运动时间为 秒( ).
(综合运用)
(1)运动开始前, , 两点的距离为 ;线段 的中点 所表示的数 .
(2)点 运动 秒后所在位置的点表示的数为 ;点 运动 秒后所在位置的点表示的数为 ;(用含 的式子表示)
(3)它们按上述方式运动, , 两点经过多少秒会相距4个单位长度?
(4)若 , 按上述方式继续运动下去,线段 的中点 能否与原点重合?若能,求出运动时间,并直接写出中点 的运动方向和运动速度;若不能,请说明理由.(当 , 两点重合,则中点 也与 , 两点重合).
答案解析部分
1.【答案】C
【解析】【解答】解:
.
故答案为:C.
【分析】根据幂的乘方法则可得。
2.【答案】B
【解析】【解答】解:A、原式是整式的乘法,不是因式分解,故本选项不符合题意;
B、原式符合因式分解的定义,是因式分解,故本选项符合题意;
C、原式的右边不是几个整式积的形式,不是因式分解,故本选项不符合题意;
D、x2-2x-1≠(x-1)2,故本选项不符合题意.
故答案为:B.
【分析】因式分解是把多项式写成几个整式积的形式的恒等变形,据此对各选项分析判断后利用排除法求解.
3.【答案】A
【解析】【解答】∵△ABC≌△CDA,
∴AB=CD,AD=BC,
∵AB=3,BC=4,
∴四边形ABCD的周长AB+BC+CD+DA=3+3+4+4=14,
故答案为:A.
【分析】根据全等三角形的性质得到AB=CD,AD=BC,进而求出四边形ABCD的周长.
4.【答案】B
【解析】【解答】解: ①三角形的内角和等于180°,是三角形内角和定理,是命题;
②对顶角相等,是对顶角的性质,是命题;
③过一点作已知直线的垂线,是作图,不是命题;
④两点确定一条直线,是直线的性质,是命题,
综上所述,属于命题是①②④.
故答案为:B.
【分析】对一件事情进行判断的语句叫命题,据此分别对每一项是否是命题进行判断即可.
5.【答案】A
【解析】【解答】解:由题意可得:a2 b2=(a b)(a+b).
故答案为:A.
【分析】由两图阴影部分的面积相等可得:a2 b2=(a b)(a+b)。
6.【答案】A
【解析】【解答】解:①两直线平行,内错角相等,故原命题为假命题;
数轴上的点与实数是一一对应的,为真命题;
经过直线外一点,有且只有一条直线与这条直线平行,故原命题为假命题;
从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离,故原命题为假命题;
在同一平面内,若直线,,则bc,故原命题为假命题;
故真命题为:.
故答案为:A.
【分析】根据真命题的定义逐项判断即可。
7.【答案】C
【解析】【解答】解:∵, , , ,
∴
∴
故答案为C.
【分析】根据 , , 可得 ,因此 ,从而得解。
8.【答案】C
【解析】【解答】解:∵长方形塑料盒的长为40,宽为30,
∴木棒最长为=50.
故答案为:C.
【分析】由题意可得:木棒的最大长度为底面长方形的对角线长,然后利用勾股定理计算即可.
9.【答案】D
【解析】【解答】①∵0是绝对值最小的有理数,∴①正确;
②∵乘以任何数得这个数的相反数,∴②不正确;
③∵数轴上原点两侧且与原点距离相等的数互为相反数,∴③不正确;
④∵负数的平方是正数,则这个数的立方也是负数,∴④不正确;
⑤∵一对相反数的平方应该相等,∴⑤不正确;
综上,不正确的结论是②③④⑤,共有4个,
故答案为:D.
【分析】利用绝对值的性质,相反数的性质及假命题的定义逐项判断即可.
10.【答案】C
【解析】【解答】解:A中 ,错误,故不符合题意;
B中 ,错误,故不符合题意;
C中 ,正确,故符合题意;
故答案为:C.
【分析】根据完全平方公式的展开式是一个三项式可判断A、B;根据平方差公式:两个数的平方差,等于这两个数的和乘以这两个数的差,可判断C.
11.【答案】n(m-1)2
【解析】【解答】解:m2n-2mn+n=n(m2-2m+1)=n(m-1)2.
【分析】先提公因式,然后运用完全平方公式进行因式分解。
12.【答案】9
【解析】【解答】解:∵x2+mx+n
=(x-2)(x-1)
=x2-3x+2
∴m=-3,n=2
∴mn=(-3)2=9
故答案为:9.
【分析】利用多项式乘多项式的计算方法可得x2-3x+2,再利用待定系数法可得m=-3,n=2,最后求出mn的值即可。
13.【答案】6
【解析】【解答】解:如图,过O作 交CD于Q,交 于H,
平分
平分
直线 与 的距离为
故答案为:
【分析】过O作 交CD于Q,交 于H,由 平分 得出由 平分 得出由此得出结论。
14.【答案】4或6
【解析】【解答】解:当腰是4时,则另两边是4,6,且4+4>6,6-4<4,满足三边关系定理,
当底边是4时,另两边长是5,5,5+4>5,5-4<5,满足三边关系定理,
∴该等腰三角形的底边为4或6,
故答案为:4或6.
【分析】利用等腰三角形的性质及三角形三边的关系求解即可。
15.【答案】65°或80°或50°.
【解析】【解答】解:(1)当∠A为顶角时,∠A=50°,则 ∠B一定为底角,∠B=65°;
(2)当∠A为底角时,∠A=50°,∠B为底角的话,∠B=50°;
(3)当∠A为底角时,∠A=50°,∠B为顶角的话,∠B=80°;
故答案为:65°或80°或50°.
【分析】根据题意得∠A=50°,再分∠A为顶角和底角,根据等腰三角形的性质和三角形的内角和定理即可求得.
16.【答案】100
【解析】【解答】∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=∠BCE=∠ACB,∠MCF=∠DCF=∠ACD,
∴∠ECF=(∠ACB+∠ACD)=90°,
∵EF∥BC ,
∴∠MEC=∠BCE,∠F=∠FCD,
∴∠MEC=∠MCE,∠MCF=∠F,
∴ME=CM=MF=5,即EF=10,
在Rt△ECF中,CE2+CF2=EF2=100.
【分析】利用角平分线的定义先推出∠ECF=90°,再根据平行线的性质及角平分线的定义可得∠MEC=∠MCE,∠MCF=∠F,从而得出ME=CM=MF=5,即EF=10,利用勾股定理可得CE2+
CF2=EF2,即可求出结论.
17.【答案】8
【解析】【解答】解:在Rt△ABC中,由勾股定理得:
AB===8(m),
即固定点A到电线杆底部B的距离是8m,
故答案为:8.
【分析】利用勾股定理先求出AB=8,再求解即可。
18.【答案】7
【解析】【解答】∵
∴
∴ ,即 =7.
【分析】将已知等式两边除以a变形求值即可.
19.【答案】解:∵x-2的算术平方根是2 ,
∴x-2=4,
x=6,
2x+y-1的立方根是3,
把x=6代入得
12+y-1=27,
y=16,
∴y-2x=16-2×6=4
∴y-2x的平方根为±2.
【解析】【分析】由算术平方根与立方根的含义列方程组,解方程组即可得到答案.
20.【答案】解:∵BF=CE,
∴BF-FC=CE-CF,即BC=EF,
∵AB∥DE,
∴∠E=∠B,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS).
【解析】【分析】根据等式的性质,由 BF=CE, 得出 BC=EF, 根据二直线平行,内错角相等得出 ∠E=∠B, 从而利用AAS判断出 △ABC≌△DEF .
21.【答案】(1)解:原式=a6﹣a6
=0
(2)解:原式=﹣4+4﹣1
=﹣1
(3)解:原式=[(﹣3)×(﹣ )]100×(﹣ )
=1100×(﹣ )
=﹣
(4)①②
【解析】【解答】(4)小明计算的过程(a3 a2)3=(a3+2)3=(a5)3=a15,他用到的公式有①②,
故答案为:①②.
【分析】(1)先算乘方,再合并同类项即可;(2)先根据负整数指数幂,零指数幂进行计算,再求出即可;(3)根据积的乘方进行计算即可;(4)根据算式得出答案即可.
22.【答案】证明:连接BD,
∵AB=AD,
∴∠ABD=∠ADB.
∵∠ABC=∠ADC,
∴∠CBD=∠CDB.
∴BC=DC.
【解析】【分析】连接BD,由等边对等角得到∠ABD=∠ADB,再由等量减去等量还是等量,得到∠CBD=∠CDB,由等角对等边得到BC=CD.
23.【答案】解:∵ ∠EPM=∠FQM ,
∴PE∥FQ,
∴ ∠PEM=∠QFM ,
又∵ ∠AEP=∠CFQ ,
∴ ∠PEM-∠AEP=∠QFM-∠CFQ ,
即∠AEM=∠CFM,
∴AB∥CD.
【解析】【分析】由同位角相等,两直线平行,得PE∥FQ,由两直线平行,同位角相等,得∠PEM=∠QFM ,结合∠AEP=∠CFQ ,根据等式的性质可以推出∠AEM=∠CFM,最后再根据同位角相等,两直线平行,得出结论.
24.【答案】解:
解:连接AC
在△ABC中, ∠B=90°,AB=4,BC=3,
所以AC=
在△ACD中, CD=12,AD=13, AC=5,
所以AC2+CD2=AD2
所以∠ACD=90°
【解析】
【分析】本题考查勾股定理及勾股定理的逆定理,先利用勾股定理计算出AC的长度,然后利用勾股定理逆定理判定△ACD为直角三角形,再把四边形ABCD的面积拆分为两个直角三角形的面积计算即可。
25.【答案】解:由题意得2a-1=9,3a+b-1=16,
解得:a=5,b=2,
则a+2b=9,
∴a+2b的平方根是 .
【解析】【分析】利用平方根及算术平方根的定义列出方程,得到a与b的值,确定出a+2b的值,即可求出平方根.
26.【答案】解:(1)证明:∵AB的垂直平分线MN交AC于点D,∴DB=DA,∴△ABD是等腰三角形;(2)∵△ABD是等腰三角形,∠A=40°,∴∠ABD=∠A=40°,∠ABC=∠C=(180°﹣40°)÷2=70°∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°;(3)∵AB的垂直平分线MN交AC于点D,AE=6,∴AB=2AE=12,∵△CBD的周长为20,∴AC+BC=20,∴△ABC的周长=AB+AC+BC=12+20=32.
【解析】【分析】(1)根据线段的垂直平分线到线段两端点的距离相等即可得证;
(2)首先利用三角形内角和求得∠ABC的度数,然后减去∠ABD的度数即可得到答案;
(3)将△ABC的周长转化为AB+AC+BC的长即可求得.
27.【答案】(1)证明:,
,
,
,
,
,
,
,
.
(2)解:如图,连接,
设,
,
,
,
由(1)已得:,
,
,
解得,
即,
由(1)已证:,
.
【解析】【分析】(1)根据题意得出,根据平行线的性质推出,即可得出结论;
(2)连接,根据平行线的性质求出答案即可。
28.【答案】(1)△OMN 是等腰直角三角形.理由如下:连接 OC.
∵AC=BC,点 O 是 AB 的中点,
∴OC⊥AB,∠1=∠2
∵∠ACB=90°,
∴∠1=∠2=45°. ∴∠A=45°.
∴∠A=∠1,∠A=∠2.
∴OA=OC.
∵AM=CN,
∴△AMO≌△CNO(SAS)
∴OM=ON,∠3=∠4.
∴∠MON=∠AOC=90°.
∴△OMN 是等腰直角三角形.
(2)由(1),△AMO≌△CNO.
∴S 四 OMCN=S△OAC.
由(1)OA=OC= 12 AB=5.
∴S 四 OMCN= 12 OA·OC= 252 。
【解析】【分析】(1)连接OC,根据等腰三角形的三线合一定理即可得到∠1=∠2,继而证明△AMO≌△CNO,即可证明三角形OMN为等腰直角三角形。
(2)根据(1)中三角形全等的性质,进行面积的计算即可。
29.【答案】(1)150;75
(2)解:如图所示:
(3)解:①当 时,可以得到点 在 的平分线上,
∴ ,
∴ ,
∴点 的坐标为 ;
② 时,过 作 于点 ,
设点 的坐标为 ,则
∴
∴
∴
∴
∴点 的坐标为 .
【解析】【解答】(1)解:∵四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=60°,∠B=75°,
∴∠D=∠B=75°,
∴∠C=360°-75°-75°-60°=150°;
故答案为150,75.
【分析】(1)由四边形ABCD是“等对角四边形”可得∠D=∠B=75°,然后根据四边形内角和为360°进行求解;
(2)根据一组对角相等而另一组对角不相等进行作图;
(3)①当∠OBP=∠OAP时,可以得到点P在△AOB的平分线上,进而推出OC=PC,据此可得点P的坐标;②当∠AOB=∠APB=90° 时,过B作BH⊥l于点H,设P(9,m),则HP=8-m,根据BH2+PH2+PC2+AC2=AB2=OA2+OB2就可得到m的值,进而得到点P的坐标.
30.【答案】(1)解:当A,B,P三点共线时,PA+PB最小短
;
原因:两点之间,线段最短.
(2)解:∵直线m是BC的垂直平分线,点P在m上,
∴点C关于直线m的对称点是点B,
则 ,
∵ ,
∵ ,
要使 周长最小,
即 最小,
当点P是直线m与AB的交点时, 最小,
即 ,此时 .
【解析】【分析】(1)利用两点之间线段最短,可知当当A,B,P三点共线时,PA+PB最小.
(2)利用垂直平分线上的点到线段两端点的距离相等,可证得BP=PC;利用△APC的周长为AP+AC+PC,而AC是定值,要使△APC的周长最小,可知AP+PC的值最小,由此可知当点P是直线m与AB的交点时,可知PA+PB最小,即可求出△APC周长的最小值.
31.【答案】(1)∠BED=∠B+∠D,理由如下
过点E作EF∥AB
∵AB∥CD
∴EF∥AB∥CD
∴∠B=∠BEF,∠D=∠DEF
∴∠BED=∠BEF+∠DEF=∠B+∠D
(2)∵∠BED=∠B+∠D,∠B=46°,∠D=58°,
∴∠BED=46°+58°=104°
【解析】【分析】(1)过点E作EF∥AB,根据平行于同一条直线的两直线平行可得EF∥AB∥CD,然后根据平行线的性质可得∠B=∠BEF,∠D=∠DEF,然后根据角的关系和等量代换即可得出结论;(2)根据(1)的结论代入各角的度数即可求出结论.
32.【答案】(1)18;
(2);
(3)解:设它们按上述方式运动, 、 两点经过 秒会相距4个单位长度,
当点 在点 左侧时,
依题意列式,得 ,解得 ;
当点 在点 右侧时,
,解得 ,
答:它们按上述方式运动, 、 两点经过2.8秒或4.4秒会相距4个单位长度.
(4)解:能.
设 、 按上述方式继续运动 秒线段的中点 能与原点重合,
根据题意列方程,可得 ,解得 .
运动开始前 点的位置是 ,运动2秒后到达原点,
由此得 点的运动方向向右,其速度为: 个单位长度.
答:运动时间为2秒,中点 点的运动方向向右,其运动速度为每秒 个单位长度.
【解析】【解答】解:(1) 、 两点的距离为: ;线段 的中点 所表示的数为 .
故答案为:18; ;
( 2 )由题意可得点 运动 秒后所在位置的点表示的数为 ;点 运动 秒后所在位置的点表示的数为 ;
故答案为: ; ;
【分析】(1)根据数轴的基本概念,由题意可得A与B两点之间的距离以及线段AB的中点表示的数.(2)由题意可得,点A运动t秒后所在位置的点表示的数等于运动开始前点A表示的数加上点A运动的路程,即-10+3t,点B运动t秒后所在位置的点表示的数等于运动开始前点B表示的数减去点B运动的路程,即8-2t.
(3)设它们按上述方式运动,A、B两点经过t秒会相遇,根据题意列方程求解即可.
(4)设A,B按上述方式继续运动秒线段的中点能与原点重合,根据题意列方程,解得k值,再由运动开始前点M的位置及k秒后所到的位置得出点M的运动方向向右及速度.
1 / 1
