华东师大版九年级数学上册第23章图形的相似单元复习题(含解析)
文档属性
| 名称 | 华东师大版九年级数学上册第23章图形的相似单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 462.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 15:07:52 | ||
图片预览




文档简介
华东师大版九年级数学上册第23章图形的相似单元复习题
一、单选题
1.已知点A(2,7), AB∥x轴,AB=3,则B点的坐标为( )
A.(5,7) B.(2,10)
C.(2,10)或(2,4) D.(5,7)或(-1,7)
2.象棋,作为中国传统棋类益智游戏,用具简单,趣味性强,深受大众喜爱,其“马走日,相走田,小卒一去不会返….”的口诀也被很多人熟知.如图,是一盘象棋的一部分,在象棋棋盘上建立平面直角坐标系,象棋中小正方形的边长视为一个单位长度,若“马”的坐标,“相”的坐标为,则“炮”的坐标为( )
A. B. C. D.
3.在平面直角坐标系中,点P(1,3)在第( )象限。
A.一 B.二 C.三 D.四
4.点M(1,2)关于x轴对称点的坐标为( )
A.(-1,2) B.(-1,-2)
C.(1,-2) D.(2,-1)
5.如图,ΔABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP AB;④AB CP=AP CB,任选一个,使ΔAPC与ΔACB相似的条件可以是( )
A.①或②或③ B.①或③或④ C.②或③或④ D.①或②或④
6.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为 ,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
7.如图,△ABC中,点D是AB的中点,点E是AC边上的动点,若△ADE与△ABC相似,则下列结论一定成立的是( )
A.E为AC的中点 B.DE是中位线或AD·AC=AE·AB
C.∠ADE=∠C D.DE∥BC或∠BDE+∠C=180°
8.如图,E是平行四边形ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式:① = ;② = ;③ = ;④ = .其中成立的是( )
A.③ B.③④ C.②③④ D.①②③④
9.如图,点 为正方形 内部两点, ,若 ,则 的长为( )
A. B. C.9 D.
二、填空题
10.点P(-2,3)到y轴距离为 .
11.如图,人字梯保险杠两端点D,E分别是梯柱AB,AC的中点,梯子打开时DE=38cm,此时梯脚的距离BC长为 cm.
12.如图,已知CB平分∠ACD,CB⊥AB垂足于点B,CD⊥BD垂足于点D,AC=5cm,BC=4cm,则BD= .
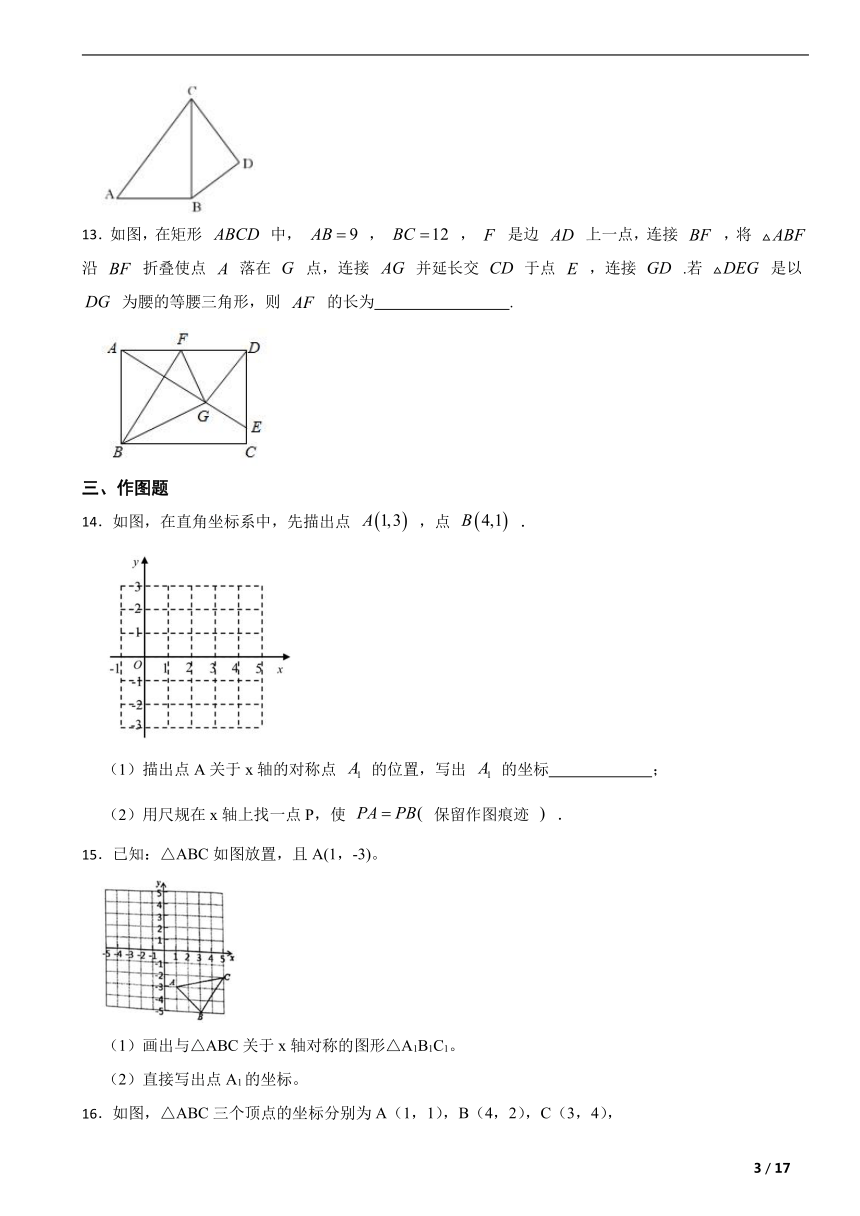
13.如图,在矩形 中, , , 是边 上一点,连接 ,将 沿 折叠使点 落在 点,连接 并延长交 于点 ,连接 .若 是以 为腰的等腰三角形,则 的长为 .
三、作图题
14.如图,在直角坐标系中,先描出点 ,点 .
(1)描出点A关于x轴的对称点 的位置,写出 的坐标 ;
(2)用尺规在x轴上找一点P,使 保留作图痕迹 .
15.已知:△ABC如图放置,且A(1,-3)。
(1)画出与△ABC关于x轴对称的图形△A1B1C1。
(2)直接写出点A1的坐标。
16.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4),
( 1 )将△ABC各顶点的横坐标保持不变,纵坐标分别减5后得到△ ,请在图中画出△ ;
( 2 )将△ABC绕点(1,0)按逆时针方向旋转90°后得到的△ ,请在图中画出△ ,并分别写出△ 的顶点坐标.
17.请用无刻度的直尺在如图1和图2中,按要求画菱形.
(1)图1是矩形ABCD,E、F分别是AB、AD的中点,以EF为边画一个菱形;
(2)图2是正方形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边画一个菱形.
四、综合题
18.如图, , 分别是 , 上的点, , 于 , 于 .若 , ,求:
(1) ;
(2) 与 的面积比.
19.如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:
(1)∠ADE和∠AED的度数;
(2)DE的长.
20.在比例尺为1:10000的地图上,有甲、乙两个相似三角形区域,其周长分别为10cm和15cm.
(1)求它们的面积比;
(2)若在地图上量得甲的面积为 ,则乙所表示的实际区域的面积是多少平方米?
21.如图1,已知A(0,a),B(b,0),且a、b满足a2﹣4a+20=8b﹣b2.
(1)求A、B两点的坐标;
(2)如图2,连接AB,若D(0,﹣6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论;
(3)如图3,在(2)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由.
22.如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
答案解析部分
1.【答案】D
【解析】【分析】AB∥x轴,则B点坐标对应y值和A点坐标对应y值相等,所以y=7.
因为AB=3,而点A对应x=2,则B对应x值为(x+3)=5或(x-3)=-1.
故选D.
【点评】本题难度较低,主要考查学生对直角坐标系上点的坐标知识点的掌握。分析与x轴平行线上点的坐标的特点是解题关键。
2.【答案】D
【解析】【解答】解∶根据题意得∶“马”的横坐标是4,“相”的纵坐标为3,可求得该平面直角坐标系的原点如图中点O,
∴“炮”的坐标为.
故答案为:∶D
【分析】根据“马”的横坐标及“相”的纵坐标,可确定原点,从而写出“炮”的坐标即可.
3.【答案】A
【解析】【分析】考查坐标象限内数的分布情况。第一象限(正,正);第二象限(负,正);第三象限(负,负);第四象限(正,负)。以题意,(1,3)属于(正,正)情况,故在第一象限。
【点评】简单题。熟悉各象限的定义即可。
4.【答案】C
【解析】两点关于x轴的对称,它们的横坐标相等,纵坐标互为相反数
故选C
5.【答案】A
【解析】【解答】①∵∠ACP=∠B,∠A=∠A,
∴△APC∽△ACB;
②∵∠APC=∠ACB,∠A=∠A,
∴△APC∽△ACB;
③∵AC2=AP AB;∠A=∠A,
∴△APC∽△ACB;
④∵AB CP=AP CB
不能得到△APC与△ACB相似;
故答案为:A.
【分析】根据相似三角形的判定来一一分析即可得出答案.
6.【答案】D
【解析】【解答】解:∵点E(﹣4,2),以O为位似中心,相似比为 ,
∴点E的对应点E′的坐标为:(﹣4× ,2× )或(﹣4×(﹣ ),2×(﹣ )),
即(﹣2,1)或(2,﹣1),
故选:D.
【分析】根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k进行计算即可.
7.【答案】D
【解析】【解答】解:如图,
∵ 点D是AB的中点,点E是AC边上的动点
①当点E运动到AC的中点时
∴DE是△ABC的中位线
∴DE∥BC
∴△ADE∽△ABC
①当点E运动到点E1时,若∠C=∠ADE1,
∵∠A=∠A
∴△ADE∽△ABC
∵∠C=∠ADE1,而∠BDE1+∠ADE1=180°
∴∠BDE1+∠C=180°
故答案为:D
【分析】分两种情况讨论:①当点E运动到AC的中点时,利用三角形中位线定理,可证得DE∥BC,即可证得结论;①当点E运动到点E1时,若∠C=∠ADE1,即∠BDE1+∠C=180°,可证得结论,即可得出答案。
8.【答案】C
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD;
∴△AEF∽△DCF,
∴ ,而AB=CD,
∴
∴②③正确;
又∵AF∥BC,
∴△AEF∽△BEC,
∴ ,
∴④正确,①不正确;
故答案为:C.
【分析】根据平行四边形的性质得出AB∥CD,则可证明△AEF∽△DCF,然后根据对应边成比例分别列式,结合AB=CD进行判断即可.
9.【答案】A
【解析】【解答】解:连接 ,交 于 ,
正方形 ,
(负根舍去)
故答案为:
【分析】连接 ,交 于 ,证明 利用相似三角形的性质求解 再利用勾股定理求解 可得 ,结合正方形的性质,勾股定理再求解 即可得到答案.
10.【答案】2
【解析】【解答】解:∵点到y轴的距离为点的横坐标的绝对值,|-2|=2,
∴点P(-2,3)到y轴距离为2.
故答案为:2.
【分析】先求出点到y轴的距离为点的横坐标的绝对值,|-2|=2,再计算求解即可。
11.【答案】76
【解析】【解答】解:∵点D,E分别是梯柱AB,AC的中点,
∴DE是△ABC的中位线,
又∵梯子打开时DE=38cm,
∴此时BC=2DE=76cm.
故答案为:76.
【分析】根据点D,E分别是梯柱AB,AC的中点,推出DE是△ABC的中位线,再由三角形中位线的性质,即平行且等于第三边的一半,即可求出梯子打开时BC的长.
12.【答案】
【解析】【解答】∵CB平分∠ACD,
∴∠ACB=∠BCD,
∵CB⊥AB垂足于点B,CD⊥BD垂足于点D,
∴∠ABC=∠BDC=90°,
∴△ABC∽△BDC,
∴ ,
在Rt△ABC中,AC=5cm,BC=4cm,
由勾股定理可得: ,
∴ ,
即 .
【分析】先证明△ABC∽△BDC,可得,再利用勾股定理求出AB的长,最后将数据代入计算即可。
13.【答案】 或
【解析】【解答】解:如图1中,当GD=GE时,过点G作GM⊥AD于M,GN⊥CD于N.设AF=x.
∵四边形ABCD是矩形,
∴AD=BC=12,∠BAF=∠ADE=90°,
由翻折的性质可知,AF=FG,BF⊥AG,
∴∠DAE+∠BAE=90°,∠ABF+∠BAE=90°,
∴∠ABF=∠DAE,
∵∠BAF=∠ADE=90°,
∴△BAF∽△ADE,
∴ ,
∴ ,
∴DE= ,
∵GM⊥AD,GN⊥CD,
∴∠GMD=∠GND=∠MDN=90°,
∴四边形GMDN是矩形,
∴GM=DN=EN= ,
∵GD=GE,
∴∠GDE=∠GED,
∵∠GDA+∠GDE=90°,∠GAD+∠GED=90°,
∴∠GDA=∠GAD,
∴GA=GD=GE,
∵GM∥DE,
∴AM=MD=6,
在Rt△FGM中,则有 ,
解得 或 (舍弃),
∴AF= .
如图2中,当DG=DE时,
由翻折的性质可知,BA=BG,
∴∠BAG=∠BGA,
∵DG=FE,
∴∠DGE=∠DEG,
∵AB∥CD,
∴∠BAE=∠DEG,
∴∠AGB=∠DGE,
∴B,G,D共线,
∵BD= ,BG=BA=9,
∴DG=DE=6,
∵△BAF∽△ADE,
∴ ,
∴ ,
∴AF= ,
综上所述,AF的值为 或 .
故答案为: 或 .
【分析】当GD=GE时,过点G作GM⊥AD于M,GN⊥CD于N,设AF=x,根据矩形的性质以及折叠的性质可得∠BAF=∠ADE=90°,∠ABF=∠DAE,进而证明△BAF∽△ADE,根据相似三角形的性质可表示出DE,然后表示出GM,求出AM的值,在Rt△FGM中,根据勾股定理可得x的值;当DG=DE时,由相似三角形的性质可得AF的值.
14.【答案】(1)
(2)如图所示:点P即为所求.
【解析】【解答】(1) ;
【分析】(1)直接利用关于直线对称点的性质得出对应点的位置进而得出答案;(2)利用线段AB的垂直平分线的作法解答即可.
15.【答案】(1)解:如图所示,△A1B1C1 即为所求,
(2)解:由图可知,A1(1,3)
【解析】【分析】(1)根据轴对称的性质及方格纸的特点,分别作出点A,B,C关于x轴的对称点A1,B1,C1,再顺次连接即可得出所求的△A1B1C1;
(2)根据关于x轴对称的点,其横坐标不变,纵坐标互为相反数即可直接得出答案.
16.【答案】解:如图所示,△A1B1C1、△A2B2C2即为所求,
A2(0,0),B2( 1,3),C2( 3,2).
【解析】【分析】(1)根据题意作出变换后的对应点,再顺次连接可得;
(2)根据旋转变换的定义作出变换后的对应点,再顺次连接可得.
17.【答案】(1)解:如图所示:四边形EFGH即为所求的菱形;
(2)解:如图所示:四边形AECF即为所求的菱形.
【解析】【分析】(1)利用正方形的性质,分别求出CD、BC的中点,然后依次连接即可;
(2)根据正方形的性质确定中心O,分别延长AE、交CD于点N,连接NO并延长交AB于点M,连接CM交BD于一点F,连接AF,CF,则四边形AECF即为所求的菱形.
18.【答案】(1)解:
(2)解:由(1)已证
【解析】【分析】(1)先根据相似三角形的判定定理得出 ,再根据相似三角形的性质即可得出答案;(2)根据相似三角形的面积之比等于其相似比的平方即可得.
19.【答案】(1)解:∵∠BAC=75°,∠ABC=40°,∴∠ACB=180°﹣∠BAC﹣∠ABC=65°.
∵△ABC∽△ADE,∴∠ADE=∠ABC=40°,∠AED=∠ACB=65°
(2)解:∵△ABC∽△ADE,∴ .
∵AB=30cm,BD=18cm,BC=20cm,∴ ,∴DE=8(cm).
【解析】【分析】(1)由三角形内角和定理和相似三角形的性质即可求解;
(2)由相似三角形的性质可得比例式,把已知的线段代入比例式计算即可求解.
20.【答案】(1)解答: ;
(2)∵ , ,
∴ ,
又∵比例尺是1:1000,
∴ .
【解析】【分析】先根据相似三角形的面积的比等于相似比的平方即可求解;首先根据两个图形的面积的比即可求得乙的面积,然后根据面积的比等于相似比的平方求得实际面积.
21.【答案】(1)解:∵a2﹣4a+20=8b﹣b2,
∴(a﹣2)2+(b﹣4)2=0,
∴a=2,b=4,
∴A(0,2),B(4,0)
(2)解:∵AD=OA+OD=8,BC=2OB=8,
∴AD=BC,
在△CAB与△AMD中, ,
∴△CAB≌△AMD,
∴AC=AM,∠ACO=∠MAD,
∵∠ACO+∠CAO=90°,
∴∠MAD+∠CAO=∠MAC=90°,
∴AC=AM,AC⊥AM
(3)解:过P作PG⊥y轴于G,
在△PAG与△HND中, ,
∴△PAG≌△HND,
∴PG=HN,AG=HD,
∴AD=GH=8,
在△PQG与△NHQ中, ,
∴△PQG≌△NHQ,
∴QG=QH= GH=4,
∴S△MQH= ×4×2=4.
【解析】【分析】(1)由a2﹣4a+20=8b﹣b2,得到(a﹣2)2+(b﹣4)2=0,求得a=2,b=4,于是得到结论;(2)由已知条件得到AD=BC,推出△CAB≌△AMD,根据全等三角形的性质得到AC=AM,∠ACO=∠MAD,由于∠ACO+∠CAO=90°,得到∠MAD+∠CAO=∠MAC=90°即可得到结论;(3)过P作PG⊥y轴于G,证得△PAG≌△HND,根据全等三角形的性质得到PG=HN,AG=HD,证得△PQG≌△NHQ,得到QG=QH= GH=4即可得到结论.
22.【答案】(1)解:∵B(8,0),C(8,6),
∴BC=6,
∴S△ABC= ×6×8=24;
(2)解:∵A(0,4) B(8,0),
∴OA=4,OB=8,
∴S四边形ABOP=S△AOB+S△AOP
= ×4×8+ ×4(﹣m)=16﹣2m,
又∵S四边形ABOP=2S△ABC=48,
∴16﹣2m=48,
解得:m=﹣16,
∴P(﹣16,1)
【解析】【分析】(1)由B、C点的坐标得到BC⊥x轴和BC的值,求出△ABC的面积;(2)由A、B点的坐标得到OA、OB的值,由四边形ABOP的面积是△ABC的面积的两倍,得到四边形ABOP的面积=△AOB的面积+△AOP的面积,求出m的值,得到P点的坐标.
1 / 1
一、单选题
1.已知点A(2,7), AB∥x轴,AB=3,则B点的坐标为( )
A.(5,7) B.(2,10)
C.(2,10)或(2,4) D.(5,7)或(-1,7)
2.象棋,作为中国传统棋类益智游戏,用具简单,趣味性强,深受大众喜爱,其“马走日,相走田,小卒一去不会返….”的口诀也被很多人熟知.如图,是一盘象棋的一部分,在象棋棋盘上建立平面直角坐标系,象棋中小正方形的边长视为一个单位长度,若“马”的坐标,“相”的坐标为,则“炮”的坐标为( )
A. B. C. D.
3.在平面直角坐标系中,点P(1,3)在第( )象限。
A.一 B.二 C.三 D.四
4.点M(1,2)关于x轴对称点的坐标为( )
A.(-1,2) B.(-1,-2)
C.(1,-2) D.(2,-1)
5.如图,ΔABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP AB;④AB CP=AP CB,任选一个,使ΔAPC与ΔACB相似的条件可以是( )
A.①或②或③ B.①或③或④ C.②或③或④ D.①或②或④
6.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为 ,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
7.如图,△ABC中,点D是AB的中点,点E是AC边上的动点,若△ADE与△ABC相似,则下列结论一定成立的是( )
A.E为AC的中点 B.DE是中位线或AD·AC=AE·AB
C.∠ADE=∠C D.DE∥BC或∠BDE+∠C=180°
8.如图,E是平行四边形ABCD的BA边的延长线上的一点,CE交AD于点F.下列各式:① = ;② = ;③ = ;④ = .其中成立的是( )
A.③ B.③④ C.②③④ D.①②③④
9.如图,点 为正方形 内部两点, ,若 ,则 的长为( )
A. B. C.9 D.
二、填空题
10.点P(-2,3)到y轴距离为 .
11.如图,人字梯保险杠两端点D,E分别是梯柱AB,AC的中点,梯子打开时DE=38cm,此时梯脚的距离BC长为 cm.
12.如图,已知CB平分∠ACD,CB⊥AB垂足于点B,CD⊥BD垂足于点D,AC=5cm,BC=4cm,则BD= .
13.如图,在矩形 中, , , 是边 上一点,连接 ,将 沿 折叠使点 落在 点,连接 并延长交 于点 ,连接 .若 是以 为腰的等腰三角形,则 的长为 .
三、作图题
14.如图,在直角坐标系中,先描出点 ,点 .
(1)描出点A关于x轴的对称点 的位置,写出 的坐标 ;
(2)用尺规在x轴上找一点P,使 保留作图痕迹 .
15.已知:△ABC如图放置,且A(1,-3)。
(1)画出与△ABC关于x轴对称的图形△A1B1C1。
(2)直接写出点A1的坐标。
16.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4),
( 1 )将△ABC各顶点的横坐标保持不变,纵坐标分别减5后得到△ ,请在图中画出△ ;
( 2 )将△ABC绕点(1,0)按逆时针方向旋转90°后得到的△ ,请在图中画出△ ,并分别写出△ 的顶点坐标.
17.请用无刻度的直尺在如图1和图2中,按要求画菱形.
(1)图1是矩形ABCD,E、F分别是AB、AD的中点,以EF为边画一个菱形;
(2)图2是正方形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边画一个菱形.
四、综合题
18.如图, , 分别是 , 上的点, , 于 , 于 .若 , ,求:
(1) ;
(2) 与 的面积比.
19.如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:
(1)∠ADE和∠AED的度数;
(2)DE的长.
20.在比例尺为1:10000的地图上,有甲、乙两个相似三角形区域,其周长分别为10cm和15cm.
(1)求它们的面积比;
(2)若在地图上量得甲的面积为 ,则乙所表示的实际区域的面积是多少平方米?
21.如图1,已知A(0,a),B(b,0),且a、b满足a2﹣4a+20=8b﹣b2.
(1)求A、B两点的坐标;
(2)如图2,连接AB,若D(0,﹣6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论;
(3)如图3,在(2)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由.
22.如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
答案解析部分
1.【答案】D
【解析】【分析】AB∥x轴,则B点坐标对应y值和A点坐标对应y值相等,所以y=7.
因为AB=3,而点A对应x=2,则B对应x值为(x+3)=5或(x-3)=-1.
故选D.
【点评】本题难度较低,主要考查学生对直角坐标系上点的坐标知识点的掌握。分析与x轴平行线上点的坐标的特点是解题关键。
2.【答案】D
【解析】【解答】解∶根据题意得∶“马”的横坐标是4,“相”的纵坐标为3,可求得该平面直角坐标系的原点如图中点O,
∴“炮”的坐标为.
故答案为:∶D
【分析】根据“马”的横坐标及“相”的纵坐标,可确定原点,从而写出“炮”的坐标即可.
3.【答案】A
【解析】【分析】考查坐标象限内数的分布情况。第一象限(正,正);第二象限(负,正);第三象限(负,负);第四象限(正,负)。以题意,(1,3)属于(正,正)情况,故在第一象限。
【点评】简单题。熟悉各象限的定义即可。
4.【答案】C
【解析】两点关于x轴的对称,它们的横坐标相等,纵坐标互为相反数
故选C
5.【答案】A
【解析】【解答】①∵∠ACP=∠B,∠A=∠A,
∴△APC∽△ACB;
②∵∠APC=∠ACB,∠A=∠A,
∴△APC∽△ACB;
③∵AC2=AP AB;∠A=∠A,
∴△APC∽△ACB;
④∵AB CP=AP CB
不能得到△APC与△ACB相似;
故答案为:A.
【分析】根据相似三角形的判定来一一分析即可得出答案.
6.【答案】D
【解析】【解答】解:∵点E(﹣4,2),以O为位似中心,相似比为 ,
∴点E的对应点E′的坐标为:(﹣4× ,2× )或(﹣4×(﹣ ),2×(﹣ )),
即(﹣2,1)或(2,﹣1),
故选:D.
【分析】根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k进行计算即可.
7.【答案】D
【解析】【解答】解:如图,
∵ 点D是AB的中点,点E是AC边上的动点
①当点E运动到AC的中点时
∴DE是△ABC的中位线
∴DE∥BC
∴△ADE∽△ABC
①当点E运动到点E1时,若∠C=∠ADE1,
∵∠A=∠A
∴△ADE∽△ABC
∵∠C=∠ADE1,而∠BDE1+∠ADE1=180°
∴∠BDE1+∠C=180°
故答案为:D
【分析】分两种情况讨论:①当点E运动到AC的中点时,利用三角形中位线定理,可证得DE∥BC,即可证得结论;①当点E运动到点E1时,若∠C=∠ADE1,即∠BDE1+∠C=180°,可证得结论,即可得出答案。
8.【答案】C
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD;
∴△AEF∽△DCF,
∴ ,而AB=CD,
∴
∴②③正确;
又∵AF∥BC,
∴△AEF∽△BEC,
∴ ,
∴④正确,①不正确;
故答案为:C.
【分析】根据平行四边形的性质得出AB∥CD,则可证明△AEF∽△DCF,然后根据对应边成比例分别列式,结合AB=CD进行判断即可.
9.【答案】A
【解析】【解答】解:连接 ,交 于 ,
正方形 ,
(负根舍去)
故答案为:
【分析】连接 ,交 于 ,证明 利用相似三角形的性质求解 再利用勾股定理求解 可得 ,结合正方形的性质,勾股定理再求解 即可得到答案.
10.【答案】2
【解析】【解答】解:∵点到y轴的距离为点的横坐标的绝对值,|-2|=2,
∴点P(-2,3)到y轴距离为2.
故答案为:2.
【分析】先求出点到y轴的距离为点的横坐标的绝对值,|-2|=2,再计算求解即可。
11.【答案】76
【解析】【解答】解:∵点D,E分别是梯柱AB,AC的中点,
∴DE是△ABC的中位线,
又∵梯子打开时DE=38cm,
∴此时BC=2DE=76cm.
故答案为:76.
【分析】根据点D,E分别是梯柱AB,AC的中点,推出DE是△ABC的中位线,再由三角形中位线的性质,即平行且等于第三边的一半,即可求出梯子打开时BC的长.
12.【答案】
【解析】【解答】∵CB平分∠ACD,
∴∠ACB=∠BCD,
∵CB⊥AB垂足于点B,CD⊥BD垂足于点D,
∴∠ABC=∠BDC=90°,
∴△ABC∽△BDC,
∴ ,
在Rt△ABC中,AC=5cm,BC=4cm,
由勾股定理可得: ,
∴ ,
即 .
【分析】先证明△ABC∽△BDC,可得,再利用勾股定理求出AB的长,最后将数据代入计算即可。
13.【答案】 或
【解析】【解答】解:如图1中,当GD=GE时,过点G作GM⊥AD于M,GN⊥CD于N.设AF=x.
∵四边形ABCD是矩形,
∴AD=BC=12,∠BAF=∠ADE=90°,
由翻折的性质可知,AF=FG,BF⊥AG,
∴∠DAE+∠BAE=90°,∠ABF+∠BAE=90°,
∴∠ABF=∠DAE,
∵∠BAF=∠ADE=90°,
∴△BAF∽△ADE,
∴ ,
∴ ,
∴DE= ,
∵GM⊥AD,GN⊥CD,
∴∠GMD=∠GND=∠MDN=90°,
∴四边形GMDN是矩形,
∴GM=DN=EN= ,
∵GD=GE,
∴∠GDE=∠GED,
∵∠GDA+∠GDE=90°,∠GAD+∠GED=90°,
∴∠GDA=∠GAD,
∴GA=GD=GE,
∵GM∥DE,
∴AM=MD=6,
在Rt△FGM中,则有 ,
解得 或 (舍弃),
∴AF= .
如图2中,当DG=DE时,
由翻折的性质可知,BA=BG,
∴∠BAG=∠BGA,
∵DG=FE,
∴∠DGE=∠DEG,
∵AB∥CD,
∴∠BAE=∠DEG,
∴∠AGB=∠DGE,
∴B,G,D共线,
∵BD= ,BG=BA=9,
∴DG=DE=6,
∵△BAF∽△ADE,
∴ ,
∴ ,
∴AF= ,
综上所述,AF的值为 或 .
故答案为: 或 .
【分析】当GD=GE时,过点G作GM⊥AD于M,GN⊥CD于N,设AF=x,根据矩形的性质以及折叠的性质可得∠BAF=∠ADE=90°,∠ABF=∠DAE,进而证明△BAF∽△ADE,根据相似三角形的性质可表示出DE,然后表示出GM,求出AM的值,在Rt△FGM中,根据勾股定理可得x的值;当DG=DE时,由相似三角形的性质可得AF的值.
14.【答案】(1)
(2)如图所示:点P即为所求.
【解析】【解答】(1) ;
【分析】(1)直接利用关于直线对称点的性质得出对应点的位置进而得出答案;(2)利用线段AB的垂直平分线的作法解答即可.
15.【答案】(1)解:如图所示,△A1B1C1 即为所求,
(2)解:由图可知,A1(1,3)
【解析】【分析】(1)根据轴对称的性质及方格纸的特点,分别作出点A,B,C关于x轴的对称点A1,B1,C1,再顺次连接即可得出所求的△A1B1C1;
(2)根据关于x轴对称的点,其横坐标不变,纵坐标互为相反数即可直接得出答案.
16.【答案】解:如图所示,△A1B1C1、△A2B2C2即为所求,
A2(0,0),B2( 1,3),C2( 3,2).
【解析】【分析】(1)根据题意作出变换后的对应点,再顺次连接可得;
(2)根据旋转变换的定义作出变换后的对应点,再顺次连接可得.
17.【答案】(1)解:如图所示:四边形EFGH即为所求的菱形;
(2)解:如图所示:四边形AECF即为所求的菱形.
【解析】【分析】(1)利用正方形的性质,分别求出CD、BC的中点,然后依次连接即可;
(2)根据正方形的性质确定中心O,分别延长AE、交CD于点N,连接NO并延长交AB于点M,连接CM交BD于一点F,连接AF,CF,则四边形AECF即为所求的菱形.
18.【答案】(1)解:
(2)解:由(1)已证
【解析】【分析】(1)先根据相似三角形的判定定理得出 ,再根据相似三角形的性质即可得出答案;(2)根据相似三角形的面积之比等于其相似比的平方即可得.
19.【答案】(1)解:∵∠BAC=75°,∠ABC=40°,∴∠ACB=180°﹣∠BAC﹣∠ABC=65°.
∵△ABC∽△ADE,∴∠ADE=∠ABC=40°,∠AED=∠ACB=65°
(2)解:∵△ABC∽△ADE,∴ .
∵AB=30cm,BD=18cm,BC=20cm,∴ ,∴DE=8(cm).
【解析】【分析】(1)由三角形内角和定理和相似三角形的性质即可求解;
(2)由相似三角形的性质可得比例式,把已知的线段代入比例式计算即可求解.
20.【答案】(1)解答: ;
(2)∵ , ,
∴ ,
又∵比例尺是1:1000,
∴ .
【解析】【分析】先根据相似三角形的面积的比等于相似比的平方即可求解;首先根据两个图形的面积的比即可求得乙的面积,然后根据面积的比等于相似比的平方求得实际面积.
21.【答案】(1)解:∵a2﹣4a+20=8b﹣b2,
∴(a﹣2)2+(b﹣4)2=0,
∴a=2,b=4,
∴A(0,2),B(4,0)
(2)解:∵AD=OA+OD=8,BC=2OB=8,
∴AD=BC,
在△CAB与△AMD中, ,
∴△CAB≌△AMD,
∴AC=AM,∠ACO=∠MAD,
∵∠ACO+∠CAO=90°,
∴∠MAD+∠CAO=∠MAC=90°,
∴AC=AM,AC⊥AM
(3)解:过P作PG⊥y轴于G,
在△PAG与△HND中, ,
∴△PAG≌△HND,
∴PG=HN,AG=HD,
∴AD=GH=8,
在△PQG与△NHQ中, ,
∴△PQG≌△NHQ,
∴QG=QH= GH=4,
∴S△MQH= ×4×2=4.
【解析】【分析】(1)由a2﹣4a+20=8b﹣b2,得到(a﹣2)2+(b﹣4)2=0,求得a=2,b=4,于是得到结论;(2)由已知条件得到AD=BC,推出△CAB≌△AMD,根据全等三角形的性质得到AC=AM,∠ACO=∠MAD,由于∠ACO+∠CAO=90°,得到∠MAD+∠CAO=∠MAC=90°即可得到结论;(3)过P作PG⊥y轴于G,证得△PAG≌△HND,根据全等三角形的性质得到PG=HN,AG=HD,证得△PQG≌△NHQ,得到QG=QH= GH=4即可得到结论.
22.【答案】(1)解:∵B(8,0),C(8,6),
∴BC=6,
∴S△ABC= ×6×8=24;
(2)解:∵A(0,4) B(8,0),
∴OA=4,OB=8,
∴S四边形ABOP=S△AOB+S△AOP
= ×4×8+ ×4(﹣m)=16﹣2m,
又∵S四边形ABOP=2S△ABC=48,
∴16﹣2m=48,
解得:m=﹣16,
∴P(﹣16,1)
【解析】【分析】(1)由B、C点的坐标得到BC⊥x轴和BC的值,求出△ABC的面积;(2)由A、B点的坐标得到OA、OB的值,由四边形ABOP的面积是△ABC的面积的两倍,得到四边形ABOP的面积=△AOB的面积+△AOP的面积,求出m的值,得到P点的坐标.
1 / 1
