华东师大版九年级数学上册第24章解直角三角形单元复习题(含解析)
文档属性
| 名称 | 华东师大版九年级数学上册第24章解直角三角形单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 670.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 15:09:43 | ||
图片预览




文档简介
华东师大版九年级数学上册第24章解直角三角形单元复习题
一、单选题
1.如果∠A是锐角,且sinA=cosA,那么∠A=( )
A.30° B.45° C.60° D.90°
2.如图,△ABC中,∠ACB=90°,AD=DB,CD=4,则AB等于( )
A.8 B.6 C.4 D.2
3.若一个三角形的两边长分别为3和6,则第三边长可能是( )
A.6 B.3 C.2 D.10
4.下列长度的三条线段能组成三角形的是( )
A.3cm、 3cm、6cm B.3cm、5cm、7cm
C.2cm、4cm、6cm D.2cm、9cm、6cm
5.平行四边形的对角线长为x、y,一边长为11,则x、y的值可能是( )
A.8和14 B.10和8 C.10和32 D.12和14
6.已知 与 全等,A、B、C的对应点分别为D、E、F,且E点在AE上,B、F、C、D四点共线,如图所示。若 , ,则下列叙述何者正确?( )
A. , B. ,
C. , D. ,
7.在中,.下列四个选项,正确的是( )
A. B. C. D.
8.等腰三角形的周长为20cm,腰长为x cm,底边长为y cm,则底边长与腰长之间的函数关系式为( )
A.y=20﹣x(0<x<10) B.y=20﹣x(10<x<20)
C.y=20﹣2x(10<x<20) D.y=20﹣2x(5<x<10)
9.等腰三角形两边的长分别为3和6,则这个等腰三角形的周长为( )
A.12 B.15 C.12或15 D.18
二、填空题
10.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是 .
11.已知等腰三角形的两边长分别为1和3,则周长等于 .
12.如图,正方形ABCD的边长为4cm,动点E、F分别从点A、C同时出发,以相同的速度分别沿AB、CD向终点B、D移动,当点E到达点B时,运动停止,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为 cm.
13.如图,在中,,把沿斜边折叠,得到,过点作于点,交于点,连结若,则的长为 ,的值为 .
三、计算题
14.计算: .
四、解答题
15.张家界大峡谷玻璃桥是我市又一闻名中外的五星景点.某校初三年级在一次研学活动中,数学研学小组设计以下方案测量桥的高度.如图,在桥面正下方的谷底选一观测点 ,观测到桥面 , 的仰角分别为 ,测得 长为320米,求观测点 到桥面 的距离.(结果保留整数,参考数据: )
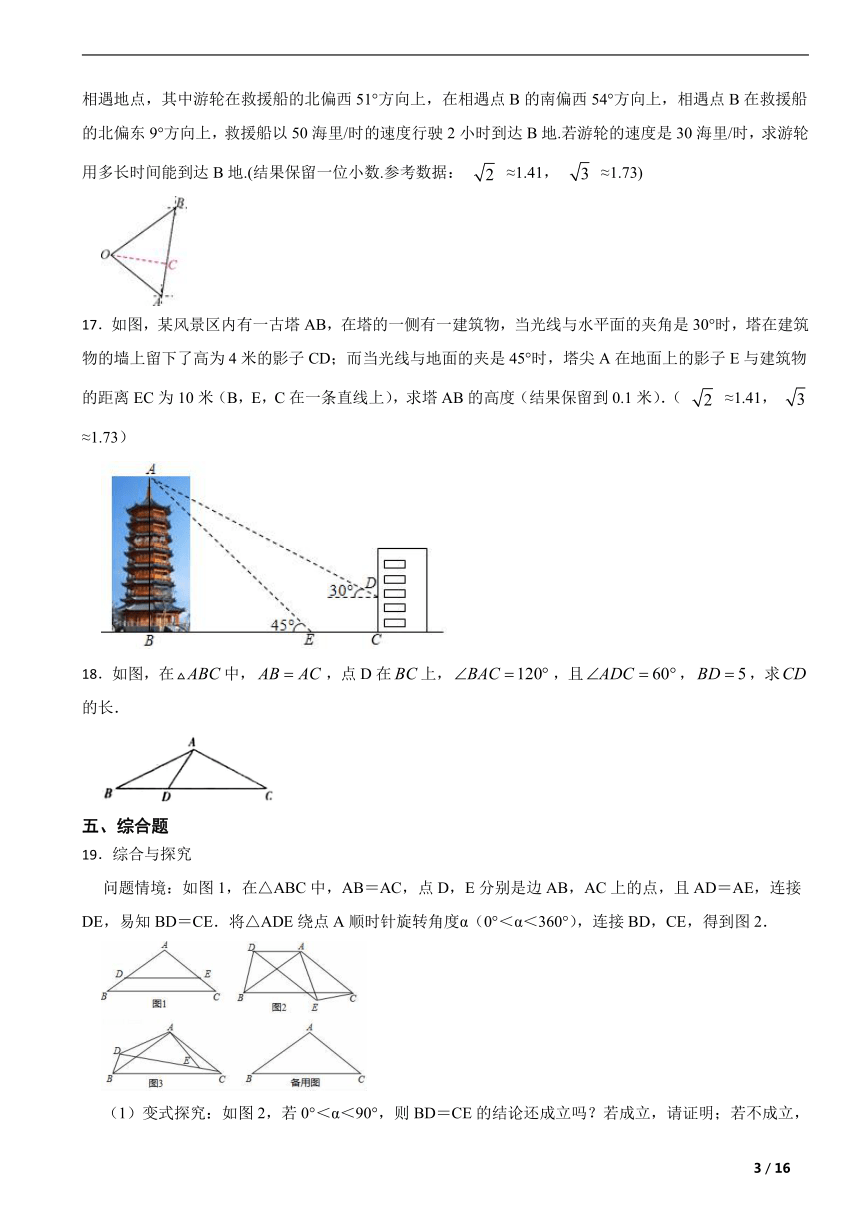
16.如图,一艘游轮在海面上点O处遇到大雾,向位于A处的救援船发出求救信号,救援船指定B地为相遇地点,其中游轮在救援船的北偏西51°方向上,在相遇点B的南偏西54°方向上,相遇点B在救援船的北偏东9°方向上,救援船以50海里/时的速度行驶2小时到达B地.若游轮的速度是30海里/时,求游轮用多长时间能到达B地.(结果保留一位小数.参考数据: ≈1.41, ≈1.73)
17.如图,某风景区内有一古塔AB,在塔的一侧有一建筑物,当光线与水平面的夹角是30°时,塔在建筑物的墙上留下了高为4米的影子CD;而当光线与地面的夹是45°时,塔尖A在地面上的影子E与建筑物的距离EC为10米(B,E,C在一条直线上),求塔AB的高度(结果保留到0.1米).( ≈1.41, ≈1.73)
18.如图,在中,,点D在上,,且,,求的长.
五、综合题
19.综合与探究
问题情境:如图1,在△ABC中,AB=AC,点D,E分别是边AB,AC上的点,且AD=AE,连接DE,易知BD=CE.将△ADE绕点A顺时针旋转角度α(0°<α<360°),连接BD,CE,得到图2.
(1)变式探究:如图2,若0°<α<90°,则BD=CE的结论还成立吗?若成立,请证明;若不成立,请说明理由;
(2)拓展延伸:若图1中的∠BAC=120°,其余条件不变,请解答下列问题:
从A,B两题中任选一题作答我选择 题
A.①在图1中,若AB=10,求BC的长;
②如图3,在△ADE绕点A顺时针旋转的过程中,当DE的延长线经过点C时,请直接写出线段AD,BD,CD之间的等量关系;
B.①在图1中,试探究BC与AB的数量关系,并说明理由;
②在△ADE绕点A顺时针旋转的过程中,当点D,E,C三点在同一条直线上时,请借助备用图探究线段AD,BD,CD之间的等量关系,并直接写出结果.
20.如图,在中,,平分交于点D,点E在线段上,点F在的延长线上,且,连接,,,.
(1)求证:四边形是菱形;
(2)若,,,求和的长.
21.如图1所示,上海中心大厦是上海市的一座超高层地标式摩天大楼,是我国最高的建筑,建筑主体共计119层.某数学小组欲测此上海中心大厦的楼高,设计出如图2所示的测量方案.具体方案如下:小组成员在地面A处通过激光测距,测得仰角 ,光路 长 ,光路 被写字楼 楼顶的一面玻璃(视为点B)反射,反射的激光束沿光路 恰好可以到达上海中心大厦 楼顶(视为点C).已知写字楼与上海中心大厦的直线距离 为 (写字楼与上海中心大厦位于同一平面),图2中的虚线为法线.(所有结果保留整数,参考数据: , , ).
(1)求写字楼 的高度.
(2)求上海中心大厦的楼高 .
22.已知:四边形 中,对角线 、 相交于点 , , .
(1)如图1,求证:四边形 为平行四边形;
(2)如图2, , , , , ,求四边形 的面积.
答案解析部分
1.【答案】B
【解析】【解答】解:∵∠A是锐角,sinA=cosA,
∴∠A=45°.
故选B.
【分析】根据题意∠A是锐角,sinA=cosA可得,∠A=45°.
2.【答案】A
【解析】【解答】解:∵∠ACB=90°,AD=BD,
∴AB=2CD=2×4=8.
故选:A.
【分析】利用直接三角形斜边上中线的性质可得AB=2CD=2×4=8。
3.【答案】A
【解析】【解答】解:设第三边为x,则3<x<9,
所以符合条件的整数为6,
故选A.
【分析】根据三角形三边关系,两边之和第三边,两边之差小于第三边即可判断.
4.【答案】B
【解析】【解答】解:∵,∴3cm、 3cm、6cm不能组成三角形,故A选项不符合题意;
∵,∴3cm、 5cm、7cm能组成三角形,故B选项符合题意;
∵,∴2cm、 4cm、6cm不能组成三角形,故C选项不符合题意;
∵,∴2cm、 9cm、6cm不能组成三角形,故D选项不符合题意.
故答案为:B.
【分析】三角形的三边关系:任意两边之和大于第三边,据此判断.
5.【答案】D
【解析】【解答】解:因为平行四边形的对角线互相平分,一边与两条对角线的一半构成三角形,所以根据三角形的三边关系进行判断:
A、根据三角形的三边关系可知:4+7=11,不能构成三角形,故此选项错误;
B、5+4<11,不能构成三角形,故此选项错误;
C、5+16>11,11+5=16,不能构成三角形,故此选项错误;
D、6+7=13>11,能构成三角形,故此选项正确.
故选:D.
【分析】根据平行四边形的性质知,平行四边形的对角线互相平分,则对角线的一半和已知的边组成三角形,再利用三角形的三边关系可逐个判断即可.
6.【答案】B
【解析】【解答】解: ≌ ,
, , ,
,
.
, ,
.
.
,
,即 .
.
, .
故答案为:B.
【分析】由 ≌ ,A、B、C的对应点分别为D、E、F,可得出 , , ,可得,由 , ,可得,由大角对大边可得 ,利用 ,可得 由此得出正确选项.
7.【答案】C
【解析】【解答】解:∵在中,,
∴,
∴,
故答案为:C.
【分析】先利用勾股定理求出BC的长,再利用锐角三角函数的定义逐项判断即可。
8.【答案】D
【解析】【解答】解:∵2x+y=20
∴y=20﹣2x,即x<10
∵两边之和大于第三边
∴x>5
故答案为:D
【分析】本题先由等腰三角形周长20=2x+y,易得y与x的函数关系式,再利用两腰之和大于底且腰、底必须是正列出x的不等式组,通过解不等式组即可确定自变量x的取值范围。
9.【答案】B
【解析】【解答】解:①当三边长为3、3、6时,
∵3+3=6,
∴不能构成三角形,
∴舍去,
②当三边长为3、6、6时,
周长为3+6+6=15;
故答案为:15.
【分析】 根据等腰三角形的性质,已知两边长,所以分两种情况讨论,即可得出答案.
10.【答案】
【解析】【解答】解:在Rt△ABC中,cosA= = ,
故答案为: .
【分析】利用锐角三角函数的定义即可求解。
11.【答案】7
【解析】【解答】若腰长为1,则1+1<3,不能组成三角形,
∴腰长只能为3,此时周长为3+3+1=7.
【分析】根据等腰三角形的性质和三边关系,判断出腰长即可求解.
12.【答案】
【解析】【解答】解:如图:
设正方形的中心为O,可证EF经过O点.
连结OB,取OB中点M,连结 MA,MG,则MA,MG为定长,
可计算得 ,
当A,M,G三点共线时,AG最小= cm,
故答案为: .
【分析】设正方形的中心为O,可证EF经过O点,连结OB,取OB中点M,连结 MA,MG,则MA,MG为定长,易得MA、MG,然后根据两点之间、线段最短的性质进行求解.
13.【答案】;
【解析】【解答】解:设 , ,
由折叠得: , , ,
,
,
,
,即 ,
,
,
,
设 ,则 , ,
由勾股定理得: ,
,
解得: ,
,
,
,
故答案为: , .
【分析】设AF=4x,BF=3x,根据折叠的性质可得∠ABC=∠ABD,BD=BC=5,DF=CF,易得cos∠ABC=cos∠ABD,根据余弦函数的概念可得BE,然后求出DE,根据勾股定理可得CE,设DF=y,则CF=y,EF= -y,根据勾股定理可得y,进而可得DF、FE,接下来根据正弦函数的概念进行计算.
14.【答案】解:原式
.
【解析】【分析】由特殊角的三角函数可得:sin45°=,tan30°=,cos30°=,cos45°=,cos60°=,从而代入特殊锐角三角函数值,再根据二次根式的混合运算法则计算即可求解.
15.【答案】解:过点 作 交 的延长线于点
由图可知: ,AM∥CD
∴∠B=∠BAM=30°,∠DCA=∠CAM=60°
∴
∴
∴
在 中,
∴ ,即
∴ (米)
答.观测点 到桥面 的距离是277米.
【解析】【分析】 过点 作 交 的延长线于点 , 根据平行线的性质得出∠B=∠BAM=30°,∠DCA=∠CAM=60°,从而求出,即得∠B=∠BAC,由等角对等边可得CA=CB=320,在中,由求出AD即可.
16.【答案】解:如图,过点O作OC⊥AB于点C.
由题意易得∠OAB=51°+9°=60°,∠OBA=54°-9°=45°.
设OC=x海里,则BC=x海里,
在Rt△OBC中,
OB= x海里,
在Rt△OAC中,
AC= = x海里.
∵AC+BC=AB,
∴ x+x=50×2,
解得x=150-50 ,
∴OB= x=(150 -50 )海里,
∴ (小时).
故游轮大约用3小时能到达B地.
【解析】【分析】过点O作OC⊥AB于点C,由题意易得∠OAB=60°,∠OBA=45°,设OC=x海里,则BC=x海里,分别在Rt△OBC、Rt△OAC中表示出OB、AC,然后根据AC+BC=AB可得x,进而求出OB,最后根据时间、速度与路程间的关系求解即可.
17.【答案】解:过点D作DF⊥AB于F,
则四边形FBCD为矩形,
∴BF=CD=4(米),
设AB=x米,则AF=(x﹣4)米,
在Rt△ABE中,∠AEB=45°,
∴BE=AB=x(米),
∴BC=(x+10)米,
在Rt△ADF中,tan∠ADF= ,即 ,
解得,x=7 +11≈23.1,
经检验,x=23.1是原方程的解,
答:塔AB的高度约为23.1米.
【解析】【分析】过点D作DF⊥AB于F,设AB=x米,则AF=(x﹣4)米,根据等腰直角三角形的形状得出BE,根据正切的定义列出方程,解方程即可得出答案。
18.【答案】解:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵∠ADC=60°,
∴∠CAD=90°,∠BAD=30°=∠B,
∴AD=BD=CD=5,
∴CD=10.
【解析】【分析】先求出∠B=∠C=30°,再利用含30°角的性质可得AD=BD=CD=5,即可得到CD=10。
19.【答案】(1)解:结论:BD=CE.
理由:如图2中,
∵∠ABC=∠DAE,
∴∠DAB=∠EAC,
∵AD=AE,AB=AC,
∴△DAB≌△EAC,
∴BD=EC.
(2)解:A:①如图1中,作AH⊥BC于H. ∵AB=AC,AH⊥BC, ∴BH=HC, ∵∠BAC=120°, ∴∠B=∠C=30°, ∴BH=AB cos30°=5 , ∴BC=10 . ②结论:CD= AD+BD. 理由:如图3中,作AH⊥CD于H. ∵△DAB≌△EAC, ∴BD=CE, 在Rt△ADH中,DH=AD cos30°= AD, ∵AD=AE,AH⊥DE, ∴DH=HE, ∵CD=DE+EC=2DH+BD= AD+BD. B:①如图1中,作AH⊥BC于H. ∵AB=AC,AH⊥BC, ∴BH=HC, ∵∠BAC=120°, ∴∠B=∠C=30°, ∴BH=AB cos30°= AB, ∴BC=2BH= AB. ②结论:CD= AD+BD. 证明方法同A②.
【解析】【分析】(1)结论:BD=CE.只要证明△DAB≌△EAC即可;(2)A:①如图1中,作AH⊥BC于H.解直角三角形即可解决问题;②结论:CD= AD+BD.如图3中,作AH⊥CD于H.由△DAB≌△EAC,推出BD=CE,在Rt△ADH中,DH=AD cos30°= AD,由AD=AE,AH⊥DE,推出DH=HE,可得CD=DE+EC=2DH+BD= AD+BD;B:①如图1中,作AH⊥BC于H.解直角三角形可得:BC=2BH= AB;
②类似A②;
20.【答案】(1)解:∵,平分,
∴,,
∵,
∴四边形是平行四边形.
∵,
∴四边形是菱形;
(2)解:∵,,,
∴在Rt△中,,
∴,
∵,
∴,
∴,
∴,
∵四边形是菱形,
∴.
【解析】【分析】(1)先证明四边形是平行四边形,再结合即可得到四边形是菱形;
(2)先求出BD的长,求出,,求出,即可得到。
21.【答案】(1)解:如图所示,过点B作BD⊥CM于点D,
∵BD⊥CM,CM⊥MN,BN⊥MN,
∴∠BDM=∠CMN=∠BNM=90°,
∴四边形BDMN是矩形,
∴BN=DM,BD=MN=576m,BD//MN,
∴∠ABD=α=37°,
由物理知识,反射角=入射角得:∠CBD=∠ABD=37°,
在Rt△ANB中, ,
m,
答:写字楼 的高度约200m.
(2)解:由(1)得 m,
在Rt△BDC中, ,
m,
∴CM=DM+CD=432+200=632m,
答:上海中心大厦的楼高CM是632m.
【解析】【分析】(1)过点B作BD⊥CM于点D, 则得出四边形BDMN是矩形,则得∠ABD=a,由反射定律得∠CBD=∠ABD=37°,最后在Rt△ANB中利用正弦函数求BN的长即可;
(2)在Rt△BDC中,由正切三角函数求出CD的长,最后根据线段间的和差关系求中心大厦的高度CM即可.
22.【答案】(1)证明:∵
∴
∵ ,
∴
∴
∴四边形 是平行四边形
(2)解:∵
∴四边形 是矩形
∴ 与 相等且互相平分
∴
∵
∴
∴ 是等边三角形
∴
∵ ,
∴
∵ ,
∴四边形 是平行四边形
作 于
∵
∴
∴
【解析】【分析】(1)根据平行线的性质可得 ,然后利用ASA即可证出 ,从而得出 OA=OC ,最后根据平行四边形的判定定理即可证出结论;(2)根据矩形的判定定理可知四边形 ABCD 是矩形,从而得出 OC=OD ,从而证出 是等边三角形,利用锐角三角函数求出CD,根据平行四边形的性质可得四边形 OCED 是平行四边形,作 于 H ,利用锐角三角函数求出DH,最后根据平行四边形的面积公式即可求出结论.
1 / 1
一、单选题
1.如果∠A是锐角,且sinA=cosA,那么∠A=( )
A.30° B.45° C.60° D.90°
2.如图,△ABC中,∠ACB=90°,AD=DB,CD=4,则AB等于( )
A.8 B.6 C.4 D.2
3.若一个三角形的两边长分别为3和6,则第三边长可能是( )
A.6 B.3 C.2 D.10
4.下列长度的三条线段能组成三角形的是( )
A.3cm、 3cm、6cm B.3cm、5cm、7cm
C.2cm、4cm、6cm D.2cm、9cm、6cm
5.平行四边形的对角线长为x、y,一边长为11,则x、y的值可能是( )
A.8和14 B.10和8 C.10和32 D.12和14
6.已知 与 全等,A、B、C的对应点分别为D、E、F,且E点在AE上,B、F、C、D四点共线,如图所示。若 , ,则下列叙述何者正确?( )
A. , B. ,
C. , D. ,
7.在中,.下列四个选项,正确的是( )
A. B. C. D.
8.等腰三角形的周长为20cm,腰长为x cm,底边长为y cm,则底边长与腰长之间的函数关系式为( )
A.y=20﹣x(0<x<10) B.y=20﹣x(10<x<20)
C.y=20﹣2x(10<x<20) D.y=20﹣2x(5<x<10)
9.等腰三角形两边的长分别为3和6,则这个等腰三角形的周长为( )
A.12 B.15 C.12或15 D.18
二、填空题
10.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是 .
11.已知等腰三角形的两边长分别为1和3,则周长等于 .
12.如图,正方形ABCD的边长为4cm,动点E、F分别从点A、C同时出发,以相同的速度分别沿AB、CD向终点B、D移动,当点E到达点B时,运动停止,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为 cm.
13.如图,在中,,把沿斜边折叠,得到,过点作于点,交于点,连结若,则的长为 ,的值为 .
三、计算题
14.计算: .
四、解答题
15.张家界大峡谷玻璃桥是我市又一闻名中外的五星景点.某校初三年级在一次研学活动中,数学研学小组设计以下方案测量桥的高度.如图,在桥面正下方的谷底选一观测点 ,观测到桥面 , 的仰角分别为 ,测得 长为320米,求观测点 到桥面 的距离.(结果保留整数,参考数据: )
16.如图,一艘游轮在海面上点O处遇到大雾,向位于A处的救援船发出求救信号,救援船指定B地为相遇地点,其中游轮在救援船的北偏西51°方向上,在相遇点B的南偏西54°方向上,相遇点B在救援船的北偏东9°方向上,救援船以50海里/时的速度行驶2小时到达B地.若游轮的速度是30海里/时,求游轮用多长时间能到达B地.(结果保留一位小数.参考数据: ≈1.41, ≈1.73)
17.如图,某风景区内有一古塔AB,在塔的一侧有一建筑物,当光线与水平面的夹角是30°时,塔在建筑物的墙上留下了高为4米的影子CD;而当光线与地面的夹是45°时,塔尖A在地面上的影子E与建筑物的距离EC为10米(B,E,C在一条直线上),求塔AB的高度(结果保留到0.1米).( ≈1.41, ≈1.73)
18.如图,在中,,点D在上,,且,,求的长.
五、综合题
19.综合与探究
问题情境:如图1,在△ABC中,AB=AC,点D,E分别是边AB,AC上的点,且AD=AE,连接DE,易知BD=CE.将△ADE绕点A顺时针旋转角度α(0°<α<360°),连接BD,CE,得到图2.
(1)变式探究:如图2,若0°<α<90°,则BD=CE的结论还成立吗?若成立,请证明;若不成立,请说明理由;
(2)拓展延伸:若图1中的∠BAC=120°,其余条件不变,请解答下列问题:
从A,B两题中任选一题作答我选择 题
A.①在图1中,若AB=10,求BC的长;
②如图3,在△ADE绕点A顺时针旋转的过程中,当DE的延长线经过点C时,请直接写出线段AD,BD,CD之间的等量关系;
B.①在图1中,试探究BC与AB的数量关系,并说明理由;
②在△ADE绕点A顺时针旋转的过程中,当点D,E,C三点在同一条直线上时,请借助备用图探究线段AD,BD,CD之间的等量关系,并直接写出结果.
20.如图,在中,,平分交于点D,点E在线段上,点F在的延长线上,且,连接,,,.
(1)求证:四边形是菱形;
(2)若,,,求和的长.
21.如图1所示,上海中心大厦是上海市的一座超高层地标式摩天大楼,是我国最高的建筑,建筑主体共计119层.某数学小组欲测此上海中心大厦的楼高,设计出如图2所示的测量方案.具体方案如下:小组成员在地面A处通过激光测距,测得仰角 ,光路 长 ,光路 被写字楼 楼顶的一面玻璃(视为点B)反射,反射的激光束沿光路 恰好可以到达上海中心大厦 楼顶(视为点C).已知写字楼与上海中心大厦的直线距离 为 (写字楼与上海中心大厦位于同一平面),图2中的虚线为法线.(所有结果保留整数,参考数据: , , ).
(1)求写字楼 的高度.
(2)求上海中心大厦的楼高 .
22.已知:四边形 中,对角线 、 相交于点 , , .
(1)如图1,求证:四边形 为平行四边形;
(2)如图2, , , , , ,求四边形 的面积.
答案解析部分
1.【答案】B
【解析】【解答】解:∵∠A是锐角,sinA=cosA,
∴∠A=45°.
故选B.
【分析】根据题意∠A是锐角,sinA=cosA可得,∠A=45°.
2.【答案】A
【解析】【解答】解:∵∠ACB=90°,AD=BD,
∴AB=2CD=2×4=8.
故选:A.
【分析】利用直接三角形斜边上中线的性质可得AB=2CD=2×4=8。
3.【答案】A
【解析】【解答】解:设第三边为x,则3<x<9,
所以符合条件的整数为6,
故选A.
【分析】根据三角形三边关系,两边之和第三边,两边之差小于第三边即可判断.
4.【答案】B
【解析】【解答】解:∵,∴3cm、 3cm、6cm不能组成三角形,故A选项不符合题意;
∵,∴3cm、 5cm、7cm能组成三角形,故B选项符合题意;
∵,∴2cm、 4cm、6cm不能组成三角形,故C选项不符合题意;
∵,∴2cm、 9cm、6cm不能组成三角形,故D选项不符合题意.
故答案为:B.
【分析】三角形的三边关系:任意两边之和大于第三边,据此判断.
5.【答案】D
【解析】【解答】解:因为平行四边形的对角线互相平分,一边与两条对角线的一半构成三角形,所以根据三角形的三边关系进行判断:
A、根据三角形的三边关系可知:4+7=11,不能构成三角形,故此选项错误;
B、5+4<11,不能构成三角形,故此选项错误;
C、5+16>11,11+5=16,不能构成三角形,故此选项错误;
D、6+7=13>11,能构成三角形,故此选项正确.
故选:D.
【分析】根据平行四边形的性质知,平行四边形的对角线互相平分,则对角线的一半和已知的边组成三角形,再利用三角形的三边关系可逐个判断即可.
6.【答案】B
【解析】【解答】解: ≌ ,
, , ,
,
.
, ,
.
.
,
,即 .
.
, .
故答案为:B.
【分析】由 ≌ ,A、B、C的对应点分别为D、E、F,可得出 , , ,可得,由 , ,可得,由大角对大边可得 ,利用 ,可得 由此得出正确选项.
7.【答案】C
【解析】【解答】解:∵在中,,
∴,
∴,
故答案为:C.
【分析】先利用勾股定理求出BC的长,再利用锐角三角函数的定义逐项判断即可。
8.【答案】D
【解析】【解答】解:∵2x+y=20
∴y=20﹣2x,即x<10
∵两边之和大于第三边
∴x>5
故答案为:D
【分析】本题先由等腰三角形周长20=2x+y,易得y与x的函数关系式,再利用两腰之和大于底且腰、底必须是正列出x的不等式组,通过解不等式组即可确定自变量x的取值范围。
9.【答案】B
【解析】【解答】解:①当三边长为3、3、6时,
∵3+3=6,
∴不能构成三角形,
∴舍去,
②当三边长为3、6、6时,
周长为3+6+6=15;
故答案为:15.
【分析】 根据等腰三角形的性质,已知两边长,所以分两种情况讨论,即可得出答案.
10.【答案】
【解析】【解答】解:在Rt△ABC中,cosA= = ,
故答案为: .
【分析】利用锐角三角函数的定义即可求解。
11.【答案】7
【解析】【解答】若腰长为1,则1+1<3,不能组成三角形,
∴腰长只能为3,此时周长为3+3+1=7.
【分析】根据等腰三角形的性质和三边关系,判断出腰长即可求解.
12.【答案】
【解析】【解答】解:如图:
设正方形的中心为O,可证EF经过O点.
连结OB,取OB中点M,连结 MA,MG,则MA,MG为定长,
可计算得 ,
当A,M,G三点共线时,AG最小= cm,
故答案为: .
【分析】设正方形的中心为O,可证EF经过O点,连结OB,取OB中点M,连结 MA,MG,则MA,MG为定长,易得MA、MG,然后根据两点之间、线段最短的性质进行求解.
13.【答案】;
【解析】【解答】解:设 , ,
由折叠得: , , ,
,
,
,
,即 ,
,
,
,
设 ,则 , ,
由勾股定理得: ,
,
解得: ,
,
,
,
故答案为: , .
【分析】设AF=4x,BF=3x,根据折叠的性质可得∠ABC=∠ABD,BD=BC=5,DF=CF,易得cos∠ABC=cos∠ABD,根据余弦函数的概念可得BE,然后求出DE,根据勾股定理可得CE,设DF=y,则CF=y,EF= -y,根据勾股定理可得y,进而可得DF、FE,接下来根据正弦函数的概念进行计算.
14.【答案】解:原式
.
【解析】【分析】由特殊角的三角函数可得:sin45°=,tan30°=,cos30°=,cos45°=,cos60°=,从而代入特殊锐角三角函数值,再根据二次根式的混合运算法则计算即可求解.
15.【答案】解:过点 作 交 的延长线于点
由图可知: ,AM∥CD
∴∠B=∠BAM=30°,∠DCA=∠CAM=60°
∴
∴
∴
在 中,
∴ ,即
∴ (米)
答.观测点 到桥面 的距离是277米.
【解析】【分析】 过点 作 交 的延长线于点 , 根据平行线的性质得出∠B=∠BAM=30°,∠DCA=∠CAM=60°,从而求出,即得∠B=∠BAC,由等角对等边可得CA=CB=320,在中,由求出AD即可.
16.【答案】解:如图,过点O作OC⊥AB于点C.
由题意易得∠OAB=51°+9°=60°,∠OBA=54°-9°=45°.
设OC=x海里,则BC=x海里,
在Rt△OBC中,
OB= x海里,
在Rt△OAC中,
AC= = x海里.
∵AC+BC=AB,
∴ x+x=50×2,
解得x=150-50 ,
∴OB= x=(150 -50 )海里,
∴ (小时).
故游轮大约用3小时能到达B地.
【解析】【分析】过点O作OC⊥AB于点C,由题意易得∠OAB=60°,∠OBA=45°,设OC=x海里,则BC=x海里,分别在Rt△OBC、Rt△OAC中表示出OB、AC,然后根据AC+BC=AB可得x,进而求出OB,最后根据时间、速度与路程间的关系求解即可.
17.【答案】解:过点D作DF⊥AB于F,
则四边形FBCD为矩形,
∴BF=CD=4(米),
设AB=x米,则AF=(x﹣4)米,
在Rt△ABE中,∠AEB=45°,
∴BE=AB=x(米),
∴BC=(x+10)米,
在Rt△ADF中,tan∠ADF= ,即 ,
解得,x=7 +11≈23.1,
经检验,x=23.1是原方程的解,
答:塔AB的高度约为23.1米.
【解析】【分析】过点D作DF⊥AB于F,设AB=x米,则AF=(x﹣4)米,根据等腰直角三角形的形状得出BE,根据正切的定义列出方程,解方程即可得出答案。
18.【答案】解:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵∠ADC=60°,
∴∠CAD=90°,∠BAD=30°=∠B,
∴AD=BD=CD=5,
∴CD=10.
【解析】【分析】先求出∠B=∠C=30°,再利用含30°角的性质可得AD=BD=CD=5,即可得到CD=10。
19.【答案】(1)解:结论:BD=CE.
理由:如图2中,
∵∠ABC=∠DAE,
∴∠DAB=∠EAC,
∵AD=AE,AB=AC,
∴△DAB≌△EAC,
∴BD=EC.
(2)解:A:①如图1中,作AH⊥BC于H. ∵AB=AC,AH⊥BC, ∴BH=HC, ∵∠BAC=120°, ∴∠B=∠C=30°, ∴BH=AB cos30°=5 , ∴BC=10 . ②结论:CD= AD+BD. 理由:如图3中,作AH⊥CD于H. ∵△DAB≌△EAC, ∴BD=CE, 在Rt△ADH中,DH=AD cos30°= AD, ∵AD=AE,AH⊥DE, ∴DH=HE, ∵CD=DE+EC=2DH+BD= AD+BD. B:①如图1中,作AH⊥BC于H. ∵AB=AC,AH⊥BC, ∴BH=HC, ∵∠BAC=120°, ∴∠B=∠C=30°, ∴BH=AB cos30°= AB, ∴BC=2BH= AB. ②结论:CD= AD+BD. 证明方法同A②.
【解析】【分析】(1)结论:BD=CE.只要证明△DAB≌△EAC即可;(2)A:①如图1中,作AH⊥BC于H.解直角三角形即可解决问题;②结论:CD= AD+BD.如图3中,作AH⊥CD于H.由△DAB≌△EAC,推出BD=CE,在Rt△ADH中,DH=AD cos30°= AD,由AD=AE,AH⊥DE,推出DH=HE,可得CD=DE+EC=2DH+BD= AD+BD;B:①如图1中,作AH⊥BC于H.解直角三角形可得:BC=2BH= AB;
②类似A②;
20.【答案】(1)解:∵,平分,
∴,,
∵,
∴四边形是平行四边形.
∵,
∴四边形是菱形;
(2)解:∵,,,
∴在Rt△中,,
∴,
∵,
∴,
∴,
∴,
∵四边形是菱形,
∴.
【解析】【分析】(1)先证明四边形是平行四边形,再结合即可得到四边形是菱形;
(2)先求出BD的长,求出,,求出,即可得到。
21.【答案】(1)解:如图所示,过点B作BD⊥CM于点D,
∵BD⊥CM,CM⊥MN,BN⊥MN,
∴∠BDM=∠CMN=∠BNM=90°,
∴四边形BDMN是矩形,
∴BN=DM,BD=MN=576m,BD//MN,
∴∠ABD=α=37°,
由物理知识,反射角=入射角得:∠CBD=∠ABD=37°,
在Rt△ANB中, ,
m,
答:写字楼 的高度约200m.
(2)解:由(1)得 m,
在Rt△BDC中, ,
m,
∴CM=DM+CD=432+200=632m,
答:上海中心大厦的楼高CM是632m.
【解析】【分析】(1)过点B作BD⊥CM于点D, 则得出四边形BDMN是矩形,则得∠ABD=a,由反射定律得∠CBD=∠ABD=37°,最后在Rt△ANB中利用正弦函数求BN的长即可;
(2)在Rt△BDC中,由正切三角函数求出CD的长,最后根据线段间的和差关系求中心大厦的高度CM即可.
22.【答案】(1)证明:∵
∴
∵ ,
∴
∴
∴四边形 是平行四边形
(2)解:∵
∴四边形 是矩形
∴ 与 相等且互相平分
∴
∵
∴
∴ 是等边三角形
∴
∵ ,
∴
∵ ,
∴四边形 是平行四边形
作 于
∵
∴
∴
【解析】【分析】(1)根据平行线的性质可得 ,然后利用ASA即可证出 ,从而得出 OA=OC ,最后根据平行四边形的判定定理即可证出结论;(2)根据矩形的判定定理可知四边形 ABCD 是矩形,从而得出 OC=OD ,从而证出 是等边三角形,利用锐角三角函数求出CD,根据平行四边形的性质可得四边形 OCED 是平行四边形,作 于 H ,利用锐角三角函数求出DH,最后根据平行四边形的面积公式即可求出结论.
1 / 1
