华东师大版九年级数学下册第27章圆单元复习题
文档属性
| 名称 | 华东师大版九年级数学下册第27章圆单元复习题 |  | |
| 格式 | docx | ||
| 文件大小 | 565.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 14:52:32 | ||
图片预览




文档简介
华东师大版九年级数学下册第27章圆单元复习题
一、单选题
1.已知⊙O的半径为5,OA=4,则点A在( )
A.⊙O内 B.⊙O上 C.⊙O外 D.无法确定
2.如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=42°,则∠ABC的度数是( )
A.21° B.24° C.42° D.48°
3.如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2 ,则∠D等于( )
A.20° B.25° C.30° D.35°
4.在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
5.如图,在⊙O中,弧AB=弧AC,∠AOB=122°,则∠AOC的度数为( )
A.122° B.120° C.61° D.58°
6.如图点A,B,C都在上,若的半径为3,,则劣弧的长是( )
A. B.π C. D.
7.如图所示的向日葵图案是用等分圆周画出的,则⊙O与半圆P的半径的比为( )
A.5﹕3 B.4﹕1 C.3﹕1 D.2﹕1
8.如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA=( )
A.30° B.45° C.60° D.67.5°
9.如图所示,圆O的弦AB垂直平分半径OC.则四边形OACB是( )
A.正方形 B.长方形
C.菱形 D.以上答案都不对
10.如图,都是的半径,交于点D.若,则的长为( ).
A.5 B.4 C.3 D.2
二、填空题
11.如图,⊙O是△ABC的外接圆,若∠AOB=100°,则∠ACB的度数是 .
12.如图,C是⊙O上一点,若,则的度数是 .
13.如图,⊙O的直径AB经过弦CD的中点H,若cos∠CDB= ,BD=5,则⊙O的半径为 .
14.如图所示,在中,是线段BC上的一个动点,以AD为直径画分别交AB,AC于E,F,连结EF,则EF的最小值为 .
三、解答题
15.如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=AB AE.
求证:DE是⊙O的切线.
16.已知:如图,BC是⊙O的弦,线段AD经过圆心O,点A在圆上,AD⊥BC,垂足为点D,若AD=8,tanA= .
(1)求弦BC的长;
(2)求⊙O半径的长.
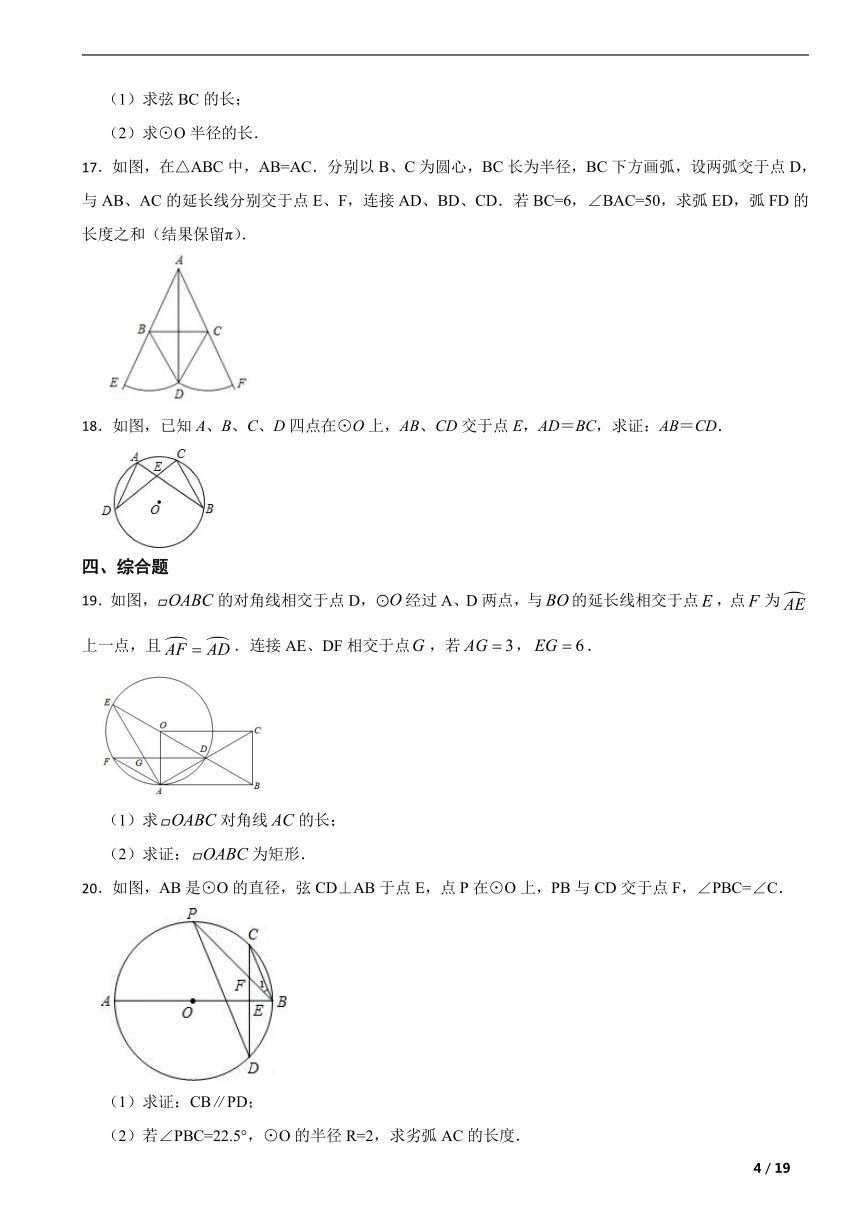
17.如图,在△ABC中,AB=AC.分别以B、C为圆心,BC长为半径,BC下方画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD、BD、CD.若BC=6,∠BAC=50,求弧ED,弧FD的长度之和(结果保留π).
18.如图,已知A、B、C、D四点在⊙O上,AB、CD交于点E,AD=BC,求证:AB=CD.
四、综合题
19.如图,的对角线相交于点D,经过A、D两点,与的延长线相交于点,点为上一点,且.连接AE、DF相交于点,若,.
(1)求对角线的长;
(2)求证:为矩形.
20.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
21.如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,且 于D,与⊙O交于点F.
(1)判断AC是否是∠DAE的平分线?并说明理由;
(2)连接OF与AC交于点G,当AG=GC=1时,求切线 的长.
22.如图,在△ABC中,AB=AC.以BC为直径画圆O分别交AB,AC于点D,E.
(1)求证:BD=CE;
(2)当△ABC中,∠B=70°且BC=12时,求 的长.
23.如图,点C是以AB为直径的半圆O上一点,且 ,AD平分 交BC于点D,CP平分 交AD于点P, , .
(1)求证:四边形CEPF为正方形;
(2)求 的最大值;
(3)求 的最小值.
答案解析部分
1.【答案】A
【解析】【解答】解:∵OA=4<5,
∴点A与⊙O的位置关系是点在圆内.
故答案为:A.
【分析】若点A到圆心的距离为d,圆的半径为r,当d>r时,点在圆外;当d=r时,点在圆上;当d2.【答案】B
【解析】【解答】解:∵直线PA与⊙O相切于点A,
∴OA⊥PA,
∴∠OAP=90°,
∴∠AOP=90°-∠P=48°,
∵∠AOP=∠B+∠OCB,
∵OB=OC,
∴∠B= ∠AOP=24°.
故答案为:B.
【分析】先利用切线的性质得到∠OAP=90°,则利用互余和计算出∠AOP=48°,再利用等腰三角形的性质和三角形外角性质可计算出∠ABC的度数.
3.【答案】C
【解析】【解答】解:如图所示:
∵AB⊥CD,CD=2 ,
∴CE= .
在Rt△OCE中,OC=OA=2,CE= ,
∴∠EOC=60°,
∴∠D=30°.
故C符合题意.
故答案为:C.
【分析】根据垂径定理求得CE的长,在Rt△OCE中,利用三角函数的定义可求得∠EOC的度数,再由圆周角定理可求出∠D的度数.
4.【答案】C
【解析】【解答】解:圆心到X轴的距离是4,到y轴的距离是3,
4=4,3<4,
∴圆与x轴相切,与y轴相交,
故选C.
【分析】首先画出图形,根据点的坐标得到圆心到X轴的距离是4,到Y轴的距离是3,根据直线与圆的位置关系即可求出答案.
5.【答案】A
【解析】【分析】由于在⊙O中,弧AB=弧AC,所以∠AOC=∠AOB=122°.
故选A.
6.【答案】C
【解析】【解答】解:如图:连接、,
,
,
∴劣弧的长.
故答案为:C.
【分析】根据圆周角与圆心角关系及扇形弧长公式得出结论。
7.【答案】D
【解析】【分析】连接OA、OP、OB;
∵向日葵图案是用等分圆周画出的,
∴此圆内接多边形是正六边形,
∴∠AOB=60°;
∵△AOB是等腰三角形,P为AB边的中点,
∴∠AOP=∠AOB=30°,△AOP是直角三角形,
∴AP=OA,即⊙O与半圆P的半径的比为2:1.
故选D.
8.【答案】D
【解析】【分析】根据等腰三角形性质和三角形外角性质求出∠COD=2∠A,求出∠D=∠COD,根据切线性质求出∠OCD=90°,即可求出答案;
【解答】∵OA=OC
∴∠A=∠ACO,
∴∠COD=∠A+∠ACO=2∠A,
∵OC=CD,
∴∠D=∠COD,
∵PD切⊙O于C,
∴∠OCD=90°,
∴∠D=∠COD=45°,
∠A=∠COD=22,.5°,
∴∠PCA=∠A+∠D=67.5°.
故选D.
【点评】本题考查了切线的性质,等腰三角形性质,三角形的外角性质的应用,熟记定理是解题的关键.
9.【答案】C
【解析】【分析】根据垂径定理和特殊四边形的判定方法求解.
【解答】由垂径定理知,OC垂直平分AB,即OC与AB互相垂直平分,所以四边形OACB是菱形.
故选C.
【点评】本题综合考查了垂径定理和菱形的判定方法.
10.【答案】B
【解析】【解答】解:∵AD=CD=8,
∴OB⊥AC.
在Rt△AOD中,
OA=,
∴OB=OA=10,
∴BD=OB-OD=10-6=4.
故答案为:B.
【分析】先根据垂径定理证明OB⊥OA;再根据勾股定理求出OA的长,因为OB=OA,所以根据BD=OB-OD即可求出BD的长.
11.【答案】50°
【解析】【解答】解:∵⊙O是△ABC的外接圆,∠AOB=100°,
∴∠ACB= ∠AOB= ×100=50°.
故答案为: 50°.
【分析】已知⊙O是△ABC的外接圆,∠AOB=100°,根据圆周角定理可求得∠ACB的度数.
12.【答案】48°
【解析】【解答】解:由圆周角定理可得,
故答案为:.
【分析】由圆周角定理可得∠AOB=2∠ACB,据此计算.
13.【答案】
【解析】【解答】解:如图,连接AC,
∵∠CDB和∠CAB所对的弧都是AC弧,
∴∠CAB=∠CDB,
∵AB为直径,H为CD的中点,
∴CH⊥AB,CB=BD=5,∠ACB=90°,
∵cos∠CDB= cos∠CDB== ,
设CA=4k,AB=5k,
∴BC==3k,
∴3k=5,即k=,
∴AB=5k=.
∴⊙O的半径为.
故答案为:.
【分析】连接AC, 根据圆周角定理求出∠CAB=∠CDB,根据垂径定理求出CH⊥AB,CB=BD=5,设CA=4k,AB=5k,根据勾股定理求出BC=3k=5,则可求出k值,从而求出AB长,即可解决问题.
14.【答案】
【解析】【解答】解:如图,连接OE、OF,过点O作OM⊥EF于点M,则EM=FM,
∵∠ACB=75°,∠ABC=45°,
∴∠BAC=60°,
∴∠EOF=120°,
∵OE=OF,
∴∠OEF=∠OFE=30°,
∴OM=OE,
∴,
当OE最小时,EF的值就最小,
∵点D是BC上的动点,AD为直径,
∴当AD⊥BC时,AD最小,即OE的值最小,
过点A作AH⊥BC于点H,
∴∠AHB=90°,
∵∠ABC=45°,
∴∠BAH=∠ABH=45°,
∴AH=BH,
∵AH2+BH2=AB2,
∴2AH2=AB2=16,
∴AH=(负值已舍),即AD的最小值为,
∴OE的最小值为,
∴EF的最小值为.
故答案为:.
【分析】连接OE、OF,过点O作OM⊥EF于点M,由垂径定理得EM=FM,由三角形的内角和定理得∠BAC=60°,由同弧所对的圆心角等于圆周角的2倍得∠EOF=120°,由等腰三角形的性质及三角形的内角和可得∠OEF=∠OFE=30°,进而根据含30°角直角三角形的性质得OM=OE,再利用勾股定理表示出,当OE最小时,EF的值就最小,又点D是BC上的动点,AD为直径,当AD⊥BC时,AD最小,即OE的值最小,过点A作AH⊥BC于点H,由等腰直角三角形的性质得AH=BH,根据勾股定理建立方程可求出AH=(负值已舍),即AD的最小值为,从而此题就不难得出答案了.
15.【答案】证明:连接DC,DO并延长交⊙O于F,连接AF.
∵P点为△ABC的内心,
∴∠BAD=∠DAE,
又∵AD2=AB AE,即 = ,
∴△BAD∽△DAE,
∴∠ADB=∠E.
又∵∠ADB=∠ACB,
∴∠ACB=∠E,BC∥DE,
∴∠CDE=∠BCD=∠BAD=∠DAC,
又∵∠CAF=∠CDF,
∴∠FDE=∠CDE+∠CDF=∠DAC+∠CAF=∠DAF=90°,
故DE是⊙O的切线.
【解析】【分析】连接DC、AF,连接DO并延长交圆O于点F,先证△BAD∽△DAE,得到∠ADB=∠E,再由平行线的性质可证∠FDE=90°可得.解答此题的关键是作出辅助线,证出△BAD∽△DAE.
16.【答案】(1)解:∵AD⊥BC, ,
∴ .
∵AD=8,∴BD=4.
又∵经过圆心O的直线AD⊥BC,
∴BC=2BD=8.
(2)解:连接OC.
设⊙O的半径为r,那么OD=8﹣r.
在△COD中,(8﹣r)2+42=r2,
∴r=5,
即⊙O的半径为5.
【解析】【分析】(1)根据题意,利用锐角三角函数的定义,在Rt△ABD中求出BD的长,再根据经过圆心O的直线AD⊥BC,就可求出BC的长。
(2)连接OC,设⊙O的半径为r,那么OD=8﹣r.利用勾股定理建立方程,求解即可求出圆的半径。
17.【答案】解:∵AB=AC,∠BAC=50°,
∴∠ABC=∠ACB=65°,
∵BD=CD=BC,
∴△BDC为等边三角形,
∴∠DBC=∠DCB=60°,
∴∠DBE=∠DCF=55°,
∵BC=6,∴BD=CD=6,
∴弧ED的长度=弧FD的长度=;
∴弧ED,弧FD的长度之和为+=.
【解析】【分析】由等腰三角形的性质得出∠ABC=∠ACB=65°,由等边三角形的性质得出∠DBC=∠DCB=60°,再由平角的定义求出∠DBE=∠DCF=55°,然后根据弧长公式求出弧ED,弧FD的长度,即可得出结果.
18.【答案】解:∵AD=BC,
∴ ,
∴ ,
即 ,
∴AB=CD.
【解析】【分析】在同圆或等圆中,两个圆心角、两条弧、两条弦中如果有一组量相等,则它们所对应的其余各组量有相等的关系.先找到弦AB与CD所对的弧,利用圆心角定理判断AB与CD所对的弧的关系即可解决.
19.【答案】(1)解:是直径,
,
,
,
又,
,
,
,
,
.
(2)证明:,
是平行四边形
,
∴AC=OB
为矩形.
【解析】【分析】(1)利用弧相等,圆周角定理可推出,可得,据此求出AD的长,由矩形的性质知AC=2AD,即得结论;
(2)根据对角线相等的平行四边形是矩形即证.
20.【答案】(1)证明:∵∠PBC=∠D,∠PBC=∠C,
∴∠C=∠D,
∴CB∥PD;
(2)解:连结OC,OD.
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴ = ,
∵∠PBC=∠C=22.5°,
∴∠BOC=∠BOD=2∠C=45°,
∴∠AOC=180°﹣∠BOC=135°,
∴劣弧AC的长为: = .
【解析】【分析】(1)根据同弧所对的圆周角相等得出 ∠PBC=∠D ,根据垂径定理得出 = ,根据等弧所对的圆周角相等得出 ∠PBC=∠C, 故 ∠C=∠D, 再根据内错角相等二直线平行得出 CB∥PD;
(2) 连结OC,OD. 根据垂径定理得出 = ,根据同弧或等弧所对的所对的圆心角等于圆周角的2倍得出 ∠BOC=∠BOD=2∠C=45°, 进而根据邻补角的定义得出∠BOC的度数,最后根据弧长计算公式l=即可算出答案。
21.【答案】(1)解:AC是∠DAE的平分线.证明:连接 .
∵DE是⊙O的切线,∴OC⊥DE,.
∵AD⊥DE,∴∠ADC=∠OCE= ,
∴AD∥OC,.
∴∠2=∠ACO,∵OA=OC,∴∠1=∠ACO,
∴∠1=∠2,∴AC是∠DAE的平分线.
(2)解:∵ =1 , ∴ ,即 .
又∠1=∠2, , ∴
又 , ∴△ 是等边三角形,
, ,.
又∠ADE= ,
∴ .
∴CE=AC=AG+CG=2
【解析】【分析】(1)先由切线性质和垂直定义得∠ADC=∠OCE,进而利用平行线的判定得∠2=∠ACO,然后利用半径相等转换为等边对等角性质,最后等量代换得角相等,即可证明AC是∠DAE的平分线.
(2)先利用等腰三角形的三线合一证明A C ⊥ O G,再由∠1=∠2根据等角的余角相等得 ∠ A F G = ∠ A O G ,从而得出△ A O F 是等边三角形,得出内角为60°后再求得 ∠ E = 30 °,然后利用直角三角形30°角的性质得出答案。
22.【答案】(1)证明:如图1,连接CD和BE,
∵BC是⊙O的直径,
∴∠BDC=∠CEB=90°,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠BCD=∠CBE,
∴ = ,
∴BD=CE.
(2)解:如图2,连接OD、OE,
∵AB=AC,∠B=70°,
∴∠ABC=∠ACB=70°,
∴∠DOC=140°,
∵OE=OC,
∴∠OEC=∠OCE=70°,
∴∠COE=40°,
∴∠DOE=100°,
∵BC=12,
∴⊙O的半径为6,
∴ 的长= = π.
【解析】【分析】(1) 连接CD和BE, 由直径所对的圆周角是直角,可得∠BDC=∠CEB=90°, 由AB=AC,可得∠ABC=∠ACB,利用三角形内角和求出∠BCD=∠CBE,从而得出 = ,继而得出BD=CE.
(2)连接OD、OE,先求出∠DOE的度数,然后利用弧长公式求解即可.
23.【答案】(1)证明:∵AB为直径,
∴ ,
∵ , ,
∴ ,
∴四边形CEPF是矩形,
∵CP平分 ,
∴ ,
∴四边形CEPF为正方形;
(2)解:过点C作CG⊥AB,如图:
由 可知,
当 最大时, 有最大值,
即 ;
由三角形的面积公式,则
,
∵ ,
∴ ,
∴ ;
∴ 的最大值是2;
(3)解:设 ,
∵ , ,
∴PE∥AC,
∴△PED∽△ACD,
∴①;
同理:PF∥BC,△PAF∽△DAC,
∴②,
由①+②,得 ,
∴ ,
即 ,
∴ ;
当x取最大值时, 有最小值;
∵AD平分 ,
∴点P为△ACB的内心,
∴PE,PF为内切圆半径;
作PH⊥AB,垂足为H,如图:
则易得AF=AH,BE=BH,
∴ ,
∴ ,
设 , , ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ 的最大值为 ;
∴ ;
∴ 的最大值为 ,
∴ ,
∴ 的最小值 ;
【解析】【分析】(1)根据圆周角定理可得∠ACB=90°,根据垂直的概念可得∠PFC=∠PEC=90°,推出四边形CEPF是矩形,根据角平分线的性质可得PF=PE,然后结合正方形的判定定理进行证明;
(2)过点C作CG⊥AB,根据△ABC的面积公式可得当CG取得最大值时,AC·BC有最大值,而CG的最大值为
AB=1,然后结合三角形的面积公式进行计算;
(3)设PE=PF=CE=CF=x,分别证明△PED∽△ACD,△PAF∽△DAC,由相似三角形的性质可得,,两式相加可得,易知点P为△ACB的内心,则PE,PF为内切圆半径,作PH⊥AB,垂足为H,则AF=AH,BE=BH,AF+BE=AB,CE=CF=
,设=acB,BC=a,AB=c=2,表示出x,由勾股定理可得a2+b2=4,则(a-b)2=a2+b2-2ab≥0,推出ab≤2,然后求出a+b的最大值,进而得到x的最大值,据此求解.
1 / 1
一、单选题
1.已知⊙O的半径为5,OA=4,则点A在( )
A.⊙O内 B.⊙O上 C.⊙O外 D.无法确定
2.如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=42°,则∠ABC的度数是( )
A.21° B.24° C.42° D.48°
3.如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2 ,则∠D等于( )
A.20° B.25° C.30° D.35°
4.在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
5.如图,在⊙O中,弧AB=弧AC,∠AOB=122°,则∠AOC的度数为( )
A.122° B.120° C.61° D.58°
6.如图点A,B,C都在上,若的半径为3,,则劣弧的长是( )
A. B.π C. D.
7.如图所示的向日葵图案是用等分圆周画出的,则⊙O与半圆P的半径的比为( )
A.5﹕3 B.4﹕1 C.3﹕1 D.2﹕1
8.如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA=( )
A.30° B.45° C.60° D.67.5°
9.如图所示,圆O的弦AB垂直平分半径OC.则四边形OACB是( )
A.正方形 B.长方形
C.菱形 D.以上答案都不对
10.如图,都是的半径,交于点D.若,则的长为( ).
A.5 B.4 C.3 D.2
二、填空题
11.如图,⊙O是△ABC的外接圆,若∠AOB=100°,则∠ACB的度数是 .
12.如图,C是⊙O上一点,若,则的度数是 .
13.如图,⊙O的直径AB经过弦CD的中点H,若cos∠CDB= ,BD=5,则⊙O的半径为 .
14.如图所示,在中,是线段BC上的一个动点,以AD为直径画分别交AB,AC于E,F,连结EF,则EF的最小值为 .
三、解答题
15.如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=AB AE.
求证:DE是⊙O的切线.
16.已知:如图,BC是⊙O的弦,线段AD经过圆心O,点A在圆上,AD⊥BC,垂足为点D,若AD=8,tanA= .
(1)求弦BC的长;
(2)求⊙O半径的长.
17.如图,在△ABC中,AB=AC.分别以B、C为圆心,BC长为半径,BC下方画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD、BD、CD.若BC=6,∠BAC=50,求弧ED,弧FD的长度之和(结果保留π).
18.如图,已知A、B、C、D四点在⊙O上,AB、CD交于点E,AD=BC,求证:AB=CD.
四、综合题
19.如图,的对角线相交于点D,经过A、D两点,与的延长线相交于点,点为上一点,且.连接AE、DF相交于点,若,.
(1)求对角线的长;
(2)求证:为矩形.
20.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
21.如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,且 于D,与⊙O交于点F.
(1)判断AC是否是∠DAE的平分线?并说明理由;
(2)连接OF与AC交于点G,当AG=GC=1时,求切线 的长.
22.如图,在△ABC中,AB=AC.以BC为直径画圆O分别交AB,AC于点D,E.
(1)求证:BD=CE;
(2)当△ABC中,∠B=70°且BC=12时,求 的长.
23.如图,点C是以AB为直径的半圆O上一点,且 ,AD平分 交BC于点D,CP平分 交AD于点P, , .
(1)求证:四边形CEPF为正方形;
(2)求 的最大值;
(3)求 的最小值.
答案解析部分
1.【答案】A
【解析】【解答】解:∵OA=4<5,
∴点A与⊙O的位置关系是点在圆内.
故答案为:A.
【分析】若点A到圆心的距离为d,圆的半径为r,当d>r时,点在圆外;当d=r时,点在圆上;当d
【解析】【解答】解:∵直线PA与⊙O相切于点A,
∴OA⊥PA,
∴∠OAP=90°,
∴∠AOP=90°-∠P=48°,
∵∠AOP=∠B+∠OCB,
∵OB=OC,
∴∠B= ∠AOP=24°.
故答案为:B.
【分析】先利用切线的性质得到∠OAP=90°,则利用互余和计算出∠AOP=48°,再利用等腰三角形的性质和三角形外角性质可计算出∠ABC的度数.
3.【答案】C
【解析】【解答】解:如图所示:
∵AB⊥CD,CD=2 ,
∴CE= .
在Rt△OCE中,OC=OA=2,CE= ,
∴∠EOC=60°,
∴∠D=30°.
故C符合题意.
故答案为:C.
【分析】根据垂径定理求得CE的长,在Rt△OCE中,利用三角函数的定义可求得∠EOC的度数,再由圆周角定理可求出∠D的度数.
4.【答案】C
【解析】【解答】解:圆心到X轴的距离是4,到y轴的距离是3,
4=4,3<4,
∴圆与x轴相切,与y轴相交,
故选C.
【分析】首先画出图形,根据点的坐标得到圆心到X轴的距离是4,到Y轴的距离是3,根据直线与圆的位置关系即可求出答案.
5.【答案】A
【解析】【分析】由于在⊙O中,弧AB=弧AC,所以∠AOC=∠AOB=122°.
故选A.
6.【答案】C
【解析】【解答】解:如图:连接、,
,
,
∴劣弧的长.
故答案为:C.
【分析】根据圆周角与圆心角关系及扇形弧长公式得出结论。
7.【答案】D
【解析】【分析】连接OA、OP、OB;
∵向日葵图案是用等分圆周画出的,
∴此圆内接多边形是正六边形,
∴∠AOB=60°;
∵△AOB是等腰三角形,P为AB边的中点,
∴∠AOP=∠AOB=30°,△AOP是直角三角形,
∴AP=OA,即⊙O与半圆P的半径的比为2:1.
故选D.
8.【答案】D
【解析】【分析】根据等腰三角形性质和三角形外角性质求出∠COD=2∠A,求出∠D=∠COD,根据切线性质求出∠OCD=90°,即可求出答案;
【解答】∵OA=OC
∴∠A=∠ACO,
∴∠COD=∠A+∠ACO=2∠A,
∵OC=CD,
∴∠D=∠COD,
∵PD切⊙O于C,
∴∠OCD=90°,
∴∠D=∠COD=45°,
∠A=∠COD=22,.5°,
∴∠PCA=∠A+∠D=67.5°.
故选D.
【点评】本题考查了切线的性质,等腰三角形性质,三角形的外角性质的应用,熟记定理是解题的关键.
9.【答案】C
【解析】【分析】根据垂径定理和特殊四边形的判定方法求解.
【解答】由垂径定理知,OC垂直平分AB,即OC与AB互相垂直平分,所以四边形OACB是菱形.
故选C.
【点评】本题综合考查了垂径定理和菱形的判定方法.
10.【答案】B
【解析】【解答】解:∵AD=CD=8,
∴OB⊥AC.
在Rt△AOD中,
OA=,
∴OB=OA=10,
∴BD=OB-OD=10-6=4.
故答案为:B.
【分析】先根据垂径定理证明OB⊥OA;再根据勾股定理求出OA的长,因为OB=OA,所以根据BD=OB-OD即可求出BD的长.
11.【答案】50°
【解析】【解答】解:∵⊙O是△ABC的外接圆,∠AOB=100°,
∴∠ACB= ∠AOB= ×100=50°.
故答案为: 50°.
【分析】已知⊙O是△ABC的外接圆,∠AOB=100°,根据圆周角定理可求得∠ACB的度数.
12.【答案】48°
【解析】【解答】解:由圆周角定理可得,
故答案为:.
【分析】由圆周角定理可得∠AOB=2∠ACB,据此计算.
13.【答案】
【解析】【解答】解:如图,连接AC,
∵∠CDB和∠CAB所对的弧都是AC弧,
∴∠CAB=∠CDB,
∵AB为直径,H为CD的中点,
∴CH⊥AB,CB=BD=5,∠ACB=90°,
∵cos∠CDB= cos∠CDB== ,
设CA=4k,AB=5k,
∴BC==3k,
∴3k=5,即k=,
∴AB=5k=.
∴⊙O的半径为.
故答案为:.
【分析】连接AC, 根据圆周角定理求出∠CAB=∠CDB,根据垂径定理求出CH⊥AB,CB=BD=5,设CA=4k,AB=5k,根据勾股定理求出BC=3k=5,则可求出k值,从而求出AB长,即可解决问题.
14.【答案】
【解析】【解答】解:如图,连接OE、OF,过点O作OM⊥EF于点M,则EM=FM,
∵∠ACB=75°,∠ABC=45°,
∴∠BAC=60°,
∴∠EOF=120°,
∵OE=OF,
∴∠OEF=∠OFE=30°,
∴OM=OE,
∴,
当OE最小时,EF的值就最小,
∵点D是BC上的动点,AD为直径,
∴当AD⊥BC时,AD最小,即OE的值最小,
过点A作AH⊥BC于点H,
∴∠AHB=90°,
∵∠ABC=45°,
∴∠BAH=∠ABH=45°,
∴AH=BH,
∵AH2+BH2=AB2,
∴2AH2=AB2=16,
∴AH=(负值已舍),即AD的最小值为,
∴OE的最小值为,
∴EF的最小值为.
故答案为:.
【分析】连接OE、OF,过点O作OM⊥EF于点M,由垂径定理得EM=FM,由三角形的内角和定理得∠BAC=60°,由同弧所对的圆心角等于圆周角的2倍得∠EOF=120°,由等腰三角形的性质及三角形的内角和可得∠OEF=∠OFE=30°,进而根据含30°角直角三角形的性质得OM=OE,再利用勾股定理表示出,当OE最小时,EF的值就最小,又点D是BC上的动点,AD为直径,当AD⊥BC时,AD最小,即OE的值最小,过点A作AH⊥BC于点H,由等腰直角三角形的性质得AH=BH,根据勾股定理建立方程可求出AH=(负值已舍),即AD的最小值为,从而此题就不难得出答案了.
15.【答案】证明:连接DC,DO并延长交⊙O于F,连接AF.
∵P点为△ABC的内心,
∴∠BAD=∠DAE,
又∵AD2=AB AE,即 = ,
∴△BAD∽△DAE,
∴∠ADB=∠E.
又∵∠ADB=∠ACB,
∴∠ACB=∠E,BC∥DE,
∴∠CDE=∠BCD=∠BAD=∠DAC,
又∵∠CAF=∠CDF,
∴∠FDE=∠CDE+∠CDF=∠DAC+∠CAF=∠DAF=90°,
故DE是⊙O的切线.
【解析】【分析】连接DC、AF,连接DO并延长交圆O于点F,先证△BAD∽△DAE,得到∠ADB=∠E,再由平行线的性质可证∠FDE=90°可得.解答此题的关键是作出辅助线,证出△BAD∽△DAE.
16.【答案】(1)解:∵AD⊥BC, ,
∴ .
∵AD=8,∴BD=4.
又∵经过圆心O的直线AD⊥BC,
∴BC=2BD=8.
(2)解:连接OC.
设⊙O的半径为r,那么OD=8﹣r.
在△COD中,(8﹣r)2+42=r2,
∴r=5,
即⊙O的半径为5.
【解析】【分析】(1)根据题意,利用锐角三角函数的定义,在Rt△ABD中求出BD的长,再根据经过圆心O的直线AD⊥BC,就可求出BC的长。
(2)连接OC,设⊙O的半径为r,那么OD=8﹣r.利用勾股定理建立方程,求解即可求出圆的半径。
17.【答案】解:∵AB=AC,∠BAC=50°,
∴∠ABC=∠ACB=65°,
∵BD=CD=BC,
∴△BDC为等边三角形,
∴∠DBC=∠DCB=60°,
∴∠DBE=∠DCF=55°,
∵BC=6,∴BD=CD=6,
∴弧ED的长度=弧FD的长度=;
∴弧ED,弧FD的长度之和为+=.
【解析】【分析】由等腰三角形的性质得出∠ABC=∠ACB=65°,由等边三角形的性质得出∠DBC=∠DCB=60°,再由平角的定义求出∠DBE=∠DCF=55°,然后根据弧长公式求出弧ED,弧FD的长度,即可得出结果.
18.【答案】解:∵AD=BC,
∴ ,
∴ ,
即 ,
∴AB=CD.
【解析】【分析】在同圆或等圆中,两个圆心角、两条弧、两条弦中如果有一组量相等,则它们所对应的其余各组量有相等的关系.先找到弦AB与CD所对的弧,利用圆心角定理判断AB与CD所对的弧的关系即可解决.
19.【答案】(1)解:是直径,
,
,
,
又,
,
,
,
,
.
(2)证明:,
是平行四边形
,
∴AC=OB
为矩形.
【解析】【分析】(1)利用弧相等,圆周角定理可推出,可得,据此求出AD的长,由矩形的性质知AC=2AD,即得结论;
(2)根据对角线相等的平行四边形是矩形即证.
20.【答案】(1)证明:∵∠PBC=∠D,∠PBC=∠C,
∴∠C=∠D,
∴CB∥PD;
(2)解:连结OC,OD.
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴ = ,
∵∠PBC=∠C=22.5°,
∴∠BOC=∠BOD=2∠C=45°,
∴∠AOC=180°﹣∠BOC=135°,
∴劣弧AC的长为: = .
【解析】【分析】(1)根据同弧所对的圆周角相等得出 ∠PBC=∠D ,根据垂径定理得出 = ,根据等弧所对的圆周角相等得出 ∠PBC=∠C, 故 ∠C=∠D, 再根据内错角相等二直线平行得出 CB∥PD;
(2) 连结OC,OD. 根据垂径定理得出 = ,根据同弧或等弧所对的所对的圆心角等于圆周角的2倍得出 ∠BOC=∠BOD=2∠C=45°, 进而根据邻补角的定义得出∠BOC的度数,最后根据弧长计算公式l=即可算出答案。
21.【答案】(1)解:AC是∠DAE的平分线.证明:连接 .
∵DE是⊙O的切线,∴OC⊥DE,.
∵AD⊥DE,∴∠ADC=∠OCE= ,
∴AD∥OC,.
∴∠2=∠ACO,∵OA=OC,∴∠1=∠ACO,
∴∠1=∠2,∴AC是∠DAE的平分线.
(2)解:∵ =1 , ∴ ,即 .
又∠1=∠2, , ∴
又 , ∴△ 是等边三角形,
, ,.
又∠ADE= ,
∴ .
∴CE=AC=AG+CG=2
【解析】【分析】(1)先由切线性质和垂直定义得∠ADC=∠OCE,进而利用平行线的判定得∠2=∠ACO,然后利用半径相等转换为等边对等角性质,最后等量代换得角相等,即可证明AC是∠DAE的平分线.
(2)先利用等腰三角形的三线合一证明A C ⊥ O G,再由∠1=∠2根据等角的余角相等得 ∠ A F G = ∠ A O G ,从而得出△ A O F 是等边三角形,得出内角为60°后再求得 ∠ E = 30 °,然后利用直角三角形30°角的性质得出答案。
22.【答案】(1)证明:如图1,连接CD和BE,
∵BC是⊙O的直径,
∴∠BDC=∠CEB=90°,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠BCD=∠CBE,
∴ = ,
∴BD=CE.
(2)解:如图2,连接OD、OE,
∵AB=AC,∠B=70°,
∴∠ABC=∠ACB=70°,
∴∠DOC=140°,
∵OE=OC,
∴∠OEC=∠OCE=70°,
∴∠COE=40°,
∴∠DOE=100°,
∵BC=12,
∴⊙O的半径为6,
∴ 的长= = π.
【解析】【分析】(1) 连接CD和BE, 由直径所对的圆周角是直角,可得∠BDC=∠CEB=90°, 由AB=AC,可得∠ABC=∠ACB,利用三角形内角和求出∠BCD=∠CBE,从而得出 = ,继而得出BD=CE.
(2)连接OD、OE,先求出∠DOE的度数,然后利用弧长公式求解即可.
23.【答案】(1)证明:∵AB为直径,
∴ ,
∵ , ,
∴ ,
∴四边形CEPF是矩形,
∵CP平分 ,
∴ ,
∴四边形CEPF为正方形;
(2)解:过点C作CG⊥AB,如图:
由 可知,
当 最大时, 有最大值,
即 ;
由三角形的面积公式,则
,
∵ ,
∴ ,
∴ ;
∴ 的最大值是2;
(3)解:设 ,
∵ , ,
∴PE∥AC,
∴△PED∽△ACD,
∴①;
同理:PF∥BC,△PAF∽△DAC,
∴②,
由①+②,得 ,
∴ ,
即 ,
∴ ;
当x取最大值时, 有最小值;
∵AD平分 ,
∴点P为△ACB的内心,
∴PE,PF为内切圆半径;
作PH⊥AB,垂足为H,如图:
则易得AF=AH,BE=BH,
∴ ,
∴ ,
设 , , ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ 的最大值为 ;
∴ ;
∴ 的最大值为 ,
∴ ,
∴ 的最小值 ;
【解析】【分析】(1)根据圆周角定理可得∠ACB=90°,根据垂直的概念可得∠PFC=∠PEC=90°,推出四边形CEPF是矩形,根据角平分线的性质可得PF=PE,然后结合正方形的判定定理进行证明;
(2)过点C作CG⊥AB,根据△ABC的面积公式可得当CG取得最大值时,AC·BC有最大值,而CG的最大值为
AB=1,然后结合三角形的面积公式进行计算;
(3)设PE=PF=CE=CF=x,分别证明△PED∽△ACD,△PAF∽△DAC,由相似三角形的性质可得,,两式相加可得,易知点P为△ACB的内心,则PE,PF为内切圆半径,作PH⊥AB,垂足为H,则AF=AH,BE=BH,AF+BE=AB,CE=CF=
,设=acB,BC=a,AB=c=2,表示出x,由勾股定理可得a2+b2=4,则(a-b)2=a2+b2-2ab≥0,推出ab≤2,然后求出a+b的最大值,进而得到x的最大值,据此求解.
1 / 1
