2023-2024学年数学七年级期末试题(青岛版)冲刺卷一含解析
文档属性
| 名称 | 2023-2024学年数学七年级期末试题(青岛版)冲刺卷一含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 727.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 12:28:00 | ||
图片预览




文档简介
绝密★启用前
2023-2024学年数学七年级期末试题(青岛版)
冲刺卷一
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
评卷人得分
一、单选题(共30分)
1.(本题3分)水星的半径用科学记数法表示大约是米,这个数据如果不用科学记数法表示应该是( )
A.24400 B.244000 C.2440000 D.24400000
2.(本题3分)已知方程,则整式的值为( )
A.a B. C. D.
3.(本题3分)中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.若零上记作,则零下可记作( )
A. B.14 C. D.
4.(本题3分)有下列生活,生产现象:
①用两个钉子就可以把木条固定在墙上:
②把弯曲的公路改直,就能缩短路程:
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④从A地到B地架设电线,总是尽可能沿着线段架设.
其中能用“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②④ D.③④
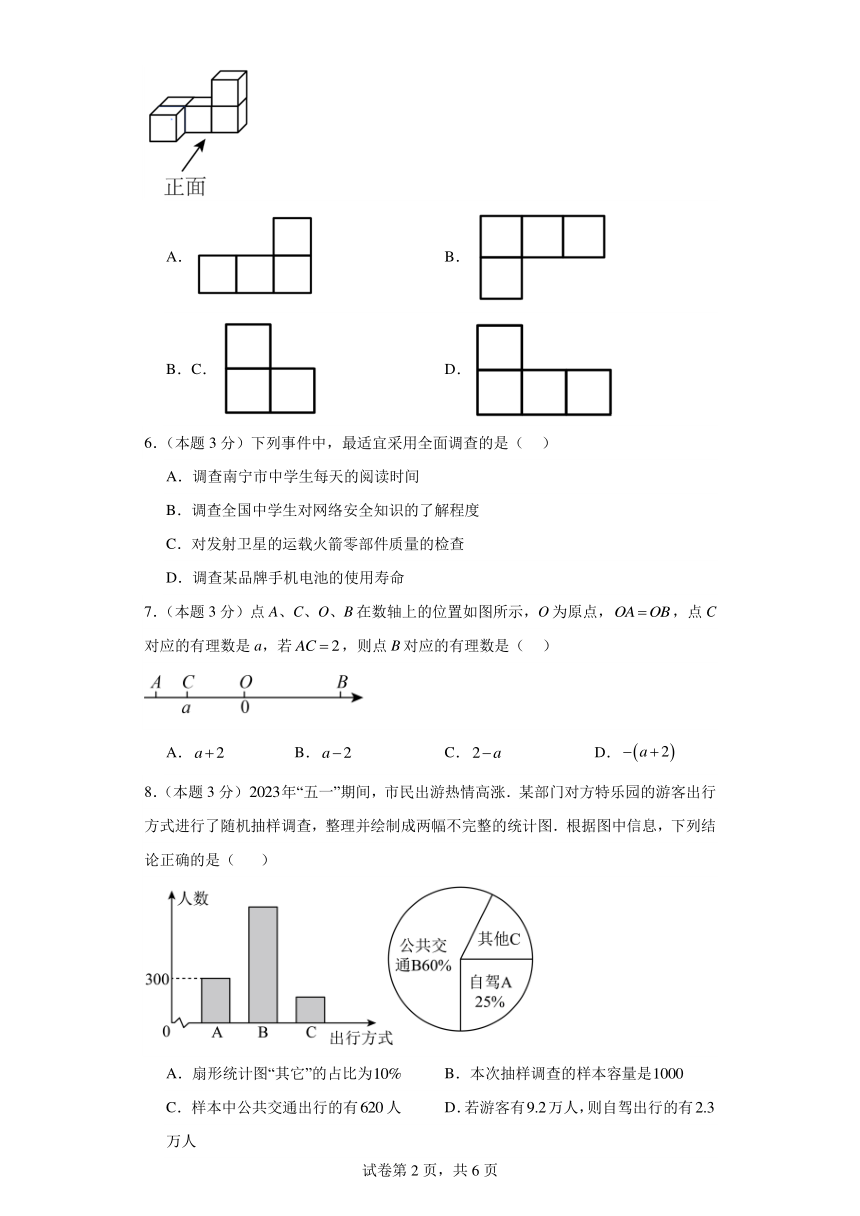
5.(本题3分)这是一个由5个相同的小立方体拼成的一个几何体.从左面看到的几何体的形状图是( )
B.
C. D.
6.(本题3分)下列事件中,最适宜采用全面调查的是( )
A.调查南宁市中学生每天的阅读时间
B.调查全国中学生对网络安全知识的了解程度
C.对发射卫星的运载火箭零部件质量的检查
D.调查某品牌手机电池的使用寿命
7.(本题3分)点A、C、O、B在数轴上的位置如图所示,O为原点,,点C对应的有理数是a,若,则点B对应的有理数是( )
A. B. C. D.
8.(本题3分)年“五一”期间,市民出游热情高涨.某部门对方特乐园的游客出行方式进行了随机抽样调查,整理并绘制成两幅不完整的统计图.根据图中信息,下列结论正确的是( )
A.扇形统计图“其它”的占比为 B.本次抽样调查的样本容量是
C.样本中公共交通出行的有人 D.若游客有万人,则自驾出行的有万人
9.(本题3分)观察如图,第1个图形中有1个正方形,第2个图形中有3个正方形,第3个图形中有6个正方形,…,依此规律,第100个图形中正方形的个数是( )个
A.5000 B.5050 C.5020 D.5100
10.(本题3分)若x,y为有理数,且,则的值为( )
A.1 B. C.2021 D.
第II卷(非选择题)
请点击修改第II卷的文字说明
评卷人得分
二、填空题(共24分)
11.(本题3分)若,互为相反数,,互为倒数,则 .
12.(本题3分)一个棱柱有10个面,则这个棱柱有 条棱.
13.(本题3分)若与是同类项,则 .
14.(本题3分)如图,在已知角的内部画射线,画1条射线,图中共有3个角;画2条射线,图中共有6个角;画3条射线,图中共有10个角;若在角的内部画2023条射线,图中共有 个角.
15.(本题3分)如图,点A、B、C是数轴上从左到右排列的三个点,分别对应的数为,b,8,某同学将刻度尺如图放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对应刻度,点C对齐刻度.则数轴上点B所对应的数b为 .
16.(本题3分)如图所示,若B,C两点把线段分成三部分,且,点P是的中点,,则的长为 .
17.(本题3分)如图是根据甲,乙两组同学最近5次体育测试的平均成绩分别绘制成的折线统计图,由统计图可知, 组同学进步更大.(选填“甲“或“乙”)
18.(本题3分)若a、b互为相反数,c、d互为倒数,数轴上表示m的点与表示的点距离5个单位长度,则 .
评卷人得分
三、解答题(共66分)
19.(本题10分)解方程:
(1); (2).
20.(本题10分)计算:
(1); (2).
21.(本题10分)作图题:如图,平面内有四个点A,B,C,D.
根据下列语句画图:
(1)画直线;
(2)画射线交直线于点E;
(3)连接并反向延长到,使得;(截取用圆规,并保留痕迹).
22.(本题10分)如图,边长为的正方形硬纸板的4个角上剪去相同的小正方形,这样可制作一个无盖的长方体纸盒,设底面边长为.
(1)这个纸盒的底面积是 ,高是 (用含a、b的代数式表示);
(2)b的部分取值及相应的纸盒容积如表所示:
1 2 3 4 5 6 7 8 9
纸盒容积 m 72 n
①请通过表格中的数据计算: , ;
②当b逐渐增大时,猜想纸盒容积的变化情况.
23.(本题12分)已知,
(1)化简:;
(2)当x为最小的正整数,y为相反数等于它本身的数时,求的值.
24.(本题14分)学生的视力状况受到社会的普遍关注.某校为了解学生的视力情况,对全校学生进行了一次视力抽样调查,小颖根据调查结果将数据整理成下表,并绘制了不完整的频数分布直方图和扇形统计图(每组包括最小值,不包括最大值).
组别 A B C D E
视力
请根据图表信息,解答下列问题:
(1)此次共调查_____了名同学;
(2)根据计算请将频数分布直方图补充完整;
(3)分别求出扇形统计图中“A组”,“C组”所在扇形对应的圆心角的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】此题主要考查科学记数法的表示方法.正确确定的值以及的值是本题的关键.科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正数;当原数的绝对值时,是负数.据此可得出结果.
【详解】解:,
故选:C
2.C
【分析】本题主要考查了等式的性质,熟知等式的性质是解题的关键:等式两边同时加上或减去同一个数或整式,等式仍然成立;等式两边同时乘以一个数或式子等式仍然成立;等式两边同时除以一个不为零的数字或式子等式仍然成立.
【详解】解:∵,
∴,
故选:C.
3.C
【分析】本题考查正数和负数,正数和负数是一组具有相反意义的量,据此即可求得答案.
【详解】解:零上记作,则零下可记作,
故选:C.
4.C
【分析】本题考查了直线和线段的知识.根据两点之间,线段最短的性质,对各个选项逐个分析,即可得到答案.
【详解】解:①用两个钉子就可以把木条固定在墙上,可用两点确定一条直线解释;
②把弯曲的公路改直,就能缩短路程,可用两点之间,线段最短解释;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,可用两点确定一条直线解释;
④从A地到地架设电线,总是尽可能沿着线段架设,可用两点之间,线段最短解释;
综上,能用“两点之间,线段最短”来解释的现象有②④.
故选:C.
5.C
【分析】本题主要考查从不同方向看几何体,从左看,注意题目和图形给定的区别.
【详解】解:从左面看到的几何体的形状图有两列,第一列有两个正方体,第二列有一个,
故选:C.
6.C
【分析】本题考查的是抽样调查和全面调查的区别,一般来说,对于具有破坏性的调查无法进行全面调查,全面调查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用全面调查.根据全面调查的特点求解即可.
【详解】解:A、调查南宁市中学生每天的阅读时间,适合用抽样调查,故选项不符合题意;
B、调查全国中学生对网络安全知识的了解程度,适合用抽样调查,故选项不符合题意;
C、对发射卫星的运载火箭零部件质量的检查,适合用全面调查,故选项符合题意;
D、调查某品牌手机电池的使用寿命,适合用抽样调查,故选项不符合题意;
故选:C.
7.C
【分析】本题主要考查在数轴上表示有理数,数轴上两点之间的距离,以及相反数的意义.由点C对应的有理数是a,,根据两点之间的距离求出点A,然后利用相反数的意义即可求解.
【详解】解:∵点C对应的有理数是a,,
∴点A对应的有理数为:,
∵,
∴A,B是一对相反数.
∴点B为,
故选:C.
8.D
【分析】选项用“”减去其它两种方式所占百分比即可判断,选项用的人数除以判断即可,选项用样本容量乘判断即可,选项用样本估计总体判断即可.
【详解】、“其它”的占比:,此选项结论错误,不符合题意,排除;
、本次抽样调查的样本容量:,此选项结论错误,不符合题意,排除;
、样本中公共交通出行的有:,此选项结论错误,不符合题意,排除;
、(万人),此选项结论正确,符合题意;
故选:.
【点睛】此题考查了条形统计图和扇形统计图,总体,个体,样本容量,样本估计总体的思想等知识,解题的关键是读懂图象信息.
9.B
【分析】本题考查了图形类规律探索,正确归纳类推出一般规律是解题关键.先根据前4个图形发现规律,再根据一般规律求解即可得.
【详解】解:由题意可知,第1个图形中正方形的个数是个,
第2个图形中正方形的个数是个,
第3个图形中正方形的个数是个,
第4个图形中正方形的个数是个,
归纳类推得:第个图形中正方形的个数是个,(为正整数),
则第100个图形中正方形的个数是个,
故选:B.
10.B
【分析】先根据绝对值和完全平方的非负性,及“两个非负数的和为0,则每一个数都为0”求出x、y的值,再代入求值即可.掌握“两个非负数的和为0,则每一个数都为0”这一性质是解题的关键.
【详解】且,,
,,,
,,
,,
.
故选:B.
11.
【分析】本题考查了相反数、倒数、代数式求值;熟练掌握“只有符号不同的两个数是互为相反数;互为倒数的两数乘积为”是解题的关键.
根据相反数的定义,倒数的定义,求出,,代入计算即可.
【详解】解:根据相反数和倒数的定义得:
∵,,
∴.
故答案为:.
12.24
【分析】本题考查了认识立体图形.先确定是几棱柱,再求解.
【详解】解:∵一个棱柱有10个面,
∴该棱柱为八棱柱,
∴这个棱柱有24条棱,
故答案为:24.
13.3
【分析】本题考查了同类项的定义,根据同类项的定义得,进而可求解,熟记:“所含字母相同,并且相同字母的指数也分别相等的项叫做同类项”是解题的关键.
【详解】解:依题意得:,
解得:,
故答案为:3.
14.2049300
【分析】本题考查了角的概念和规律探索,解题的关键在于推导得出一般性规律.根据角的个数,推导出一般性规律,进而求解即可.
【详解】解:由题意知画1条射线,图中共有个角,
画2条射线,图中共有个角,
画3条射线,图中共有个角,
由此推导出一般性规律:画条射线,图中共有个角,
∴当时,,
故答案为:2049300.
15.2
【分析】本题主要考查了数轴上两点的距离计算,先求出,再根据题意可得,则.
【详解】解:∵点A、B、C是数轴上从左到右排列的三个点,分别对应的数为,b,8,
∴,
∵刻度尺上的数字0对齐数轴上的点A,发现点B对应刻度,点C对齐刻度,
∴,
∴,
故答案为:2.
16.
【分析】根据线段比例,设设,则,列出一元一次方程求解即可.本题考查两点间的距离,弄清楚线段之间的数量关系是关键.
【详解】解:∵,
∴设,
则,
∵点P是的中点,
∴,
∴,
∵,
∴,
解得,
∴.
故答案为:.
17.甲
【分析】根据统计图中所反映的数据的变化情况进行判断.
【详解】解:甲组的成绩变化从70到90,乙组的成绩变化是从70到85,所以甲组进步更大.
故答案为:甲.
【点睛】考查折线统计图的意义和制作方法,同时注意折线统计图容易给人造成错觉的原因,要正确的识别统计图,得出客观的结论.
18.2或/或2
【分析】本题主要考查了相反数的定义,倒数的定义,数轴上两点之间的距离,解题的关键是掌握相反数相加得0,乘积为1的两个数互为倒数,以及数轴上两点之间距离的表示方法.根据题意得出,,或,将其代入求解即可.
【详解】解:∵a、b互为相反数,
∴,
∵c、d互为倒数,
∴,
∵数轴上表示m的点与表示的点距离5个单位长度,
∴或,
∴,
或,
故答案为:2或.
19.(1);
(2).
【分析】本题考查了解一元一次方程,能正确根据等式的性质进行变形是解此题的关键.
(1)移项,合并同类项,系数化成1即可;
(2)去分母,去括号,移项,合并同类项,系数化成1即可.
【详解】(1)解:,
移项,得,
合并同类项,得,
系数化成1,得;
(2)解:
去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化成1,得;
20.(1)
(2)
【分析】本题考查的是有理数的混合运算,掌握混合运算的运算顺序是解本题的关键;
(1)先化为省略加号的和的形式,再计算即可;
(2)先计算乘方运算,再计算乘除运算,最后计算加减运算即可.
【详解】(1)解:
;
(2)
;
21.(1)见解析
(2)见解析
(3)见解析
【分析】本题主要考查了线段、直线、射线的作图,
(1)根据直线的定义,作图即可;
(2)根据射线的定义,结合(1)的结论,作图即可;
(3)延长,然后以点为圆心,以长为半径,在的延长线上,截取,即.
【详解】(1)解:如图,直线为所求,
(2)如图所示,
(3)如图所示,
22.(1);
(2)①;;②当逐渐增大时,纸盒容积的变化情况:先随着的增大而增大,后随着的增大而减小,
【分析】本题主要考查了列代数式,一元一次方程的应用,代数式求值:
(1)根据正方形的面积公式结合图形进行计算即可;
(2)①利用纸盒的容积的公式求出的值,然后把,代入进行计算即可,②通过计算,2,3,4,5,6,7,8,9时,纸盒的容积即可解答;
【详解】(1)解:由题意得,这个纸盒的底面积是,高是,
故答案为:;;
(2)解:∵当时,纸盒容积为,
∴,
解得,
∴,
故答案为:;;
②当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
∴当逐渐增大时,纸盒容积的变化情况:先随着的增大而增大,后随着的增大而减小.
23.(1)
(2)
【分析】本题考查了整式的加减运算,以及化简求值,相反数的定义
(1)先把表示出来,再与进行减法运算,合并同类项,即可作答.
(2)依题意,,,代入,即可作答.
【详解】(1)解:∵,,
∴
;
(2)解:由题意知,,
原式.
24.(1);
(2)图见详解;
(3),;
【分析】本题考查求样本容量,补全直方图,求扇形同统计图的圆心角度数,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)根据的频数及占比直接求解即可得到答案;
(2)结合(1)求出和的量,补全图形即可得到答案;
(3)利用乘以占比即可得到答案.
【详解】(1)解:由图像可得,
此次共调查了:(人),
故答案为:;
(2)解:由图像及(1)得,
的人数为:(人),
的人数为:(人),
∴频数分布直方图如图所示,
;
(3)解:由图形及(2)得,
组的圆心角为:,
组的圆心角为:.
答案第1页,共2页
答案第1页,共2页
2023-2024学年数学七年级期末试题(青岛版)
冲刺卷一
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
评卷人得分
一、单选题(共30分)
1.(本题3分)水星的半径用科学记数法表示大约是米,这个数据如果不用科学记数法表示应该是( )
A.24400 B.244000 C.2440000 D.24400000
2.(本题3分)已知方程,则整式的值为( )
A.a B. C. D.
3.(本题3分)中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.若零上记作,则零下可记作( )
A. B.14 C. D.
4.(本题3分)有下列生活,生产现象:
①用两个钉子就可以把木条固定在墙上:
②把弯曲的公路改直,就能缩短路程:
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④从A地到B地架设电线,总是尽可能沿着线段架设.
其中能用“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②④ D.③④
5.(本题3分)这是一个由5个相同的小立方体拼成的一个几何体.从左面看到的几何体的形状图是( )
B.
C. D.
6.(本题3分)下列事件中,最适宜采用全面调查的是( )
A.调查南宁市中学生每天的阅读时间
B.调查全国中学生对网络安全知识的了解程度
C.对发射卫星的运载火箭零部件质量的检查
D.调查某品牌手机电池的使用寿命
7.(本题3分)点A、C、O、B在数轴上的位置如图所示,O为原点,,点C对应的有理数是a,若,则点B对应的有理数是( )
A. B. C. D.
8.(本题3分)年“五一”期间,市民出游热情高涨.某部门对方特乐园的游客出行方式进行了随机抽样调查,整理并绘制成两幅不完整的统计图.根据图中信息,下列结论正确的是( )
A.扇形统计图“其它”的占比为 B.本次抽样调查的样本容量是
C.样本中公共交通出行的有人 D.若游客有万人,则自驾出行的有万人
9.(本题3分)观察如图,第1个图形中有1个正方形,第2个图形中有3个正方形,第3个图形中有6个正方形,…,依此规律,第100个图形中正方形的个数是( )个
A.5000 B.5050 C.5020 D.5100
10.(本题3分)若x,y为有理数,且,则的值为( )
A.1 B. C.2021 D.
第II卷(非选择题)
请点击修改第II卷的文字说明
评卷人得分
二、填空题(共24分)
11.(本题3分)若,互为相反数,,互为倒数,则 .
12.(本题3分)一个棱柱有10个面,则这个棱柱有 条棱.
13.(本题3分)若与是同类项,则 .
14.(本题3分)如图,在已知角的内部画射线,画1条射线,图中共有3个角;画2条射线,图中共有6个角;画3条射线,图中共有10个角;若在角的内部画2023条射线,图中共有 个角.
15.(本题3分)如图,点A、B、C是数轴上从左到右排列的三个点,分别对应的数为,b,8,某同学将刻度尺如图放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对应刻度,点C对齐刻度.则数轴上点B所对应的数b为 .
16.(本题3分)如图所示,若B,C两点把线段分成三部分,且,点P是的中点,,则的长为 .
17.(本题3分)如图是根据甲,乙两组同学最近5次体育测试的平均成绩分别绘制成的折线统计图,由统计图可知, 组同学进步更大.(选填“甲“或“乙”)
18.(本题3分)若a、b互为相反数,c、d互为倒数,数轴上表示m的点与表示的点距离5个单位长度,则 .
评卷人得分
三、解答题(共66分)
19.(本题10分)解方程:
(1); (2).
20.(本题10分)计算:
(1); (2).
21.(本题10分)作图题:如图,平面内有四个点A,B,C,D.
根据下列语句画图:
(1)画直线;
(2)画射线交直线于点E;
(3)连接并反向延长到,使得;(截取用圆规,并保留痕迹).
22.(本题10分)如图,边长为的正方形硬纸板的4个角上剪去相同的小正方形,这样可制作一个无盖的长方体纸盒,设底面边长为.
(1)这个纸盒的底面积是 ,高是 (用含a、b的代数式表示);
(2)b的部分取值及相应的纸盒容积如表所示:
1 2 3 4 5 6 7 8 9
纸盒容积 m 72 n
①请通过表格中的数据计算: , ;
②当b逐渐增大时,猜想纸盒容积的变化情况.
23.(本题12分)已知,
(1)化简:;
(2)当x为最小的正整数,y为相反数等于它本身的数时,求的值.
24.(本题14分)学生的视力状况受到社会的普遍关注.某校为了解学生的视力情况,对全校学生进行了一次视力抽样调查,小颖根据调查结果将数据整理成下表,并绘制了不完整的频数分布直方图和扇形统计图(每组包括最小值,不包括最大值).
组别 A B C D E
视力
请根据图表信息,解答下列问题:
(1)此次共调查_____了名同学;
(2)根据计算请将频数分布直方图补充完整;
(3)分别求出扇形统计图中“A组”,“C组”所在扇形对应的圆心角的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】此题主要考查科学记数法的表示方法.正确确定的值以及的值是本题的关键.科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正数;当原数的绝对值时,是负数.据此可得出结果.
【详解】解:,
故选:C
2.C
【分析】本题主要考查了等式的性质,熟知等式的性质是解题的关键:等式两边同时加上或减去同一个数或整式,等式仍然成立;等式两边同时乘以一个数或式子等式仍然成立;等式两边同时除以一个不为零的数字或式子等式仍然成立.
【详解】解:∵,
∴,
故选:C.
3.C
【分析】本题考查正数和负数,正数和负数是一组具有相反意义的量,据此即可求得答案.
【详解】解:零上记作,则零下可记作,
故选:C.
4.C
【分析】本题考查了直线和线段的知识.根据两点之间,线段最短的性质,对各个选项逐个分析,即可得到答案.
【详解】解:①用两个钉子就可以把木条固定在墙上,可用两点确定一条直线解释;
②把弯曲的公路改直,就能缩短路程,可用两点之间,线段最短解释;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,可用两点确定一条直线解释;
④从A地到地架设电线,总是尽可能沿着线段架设,可用两点之间,线段最短解释;
综上,能用“两点之间,线段最短”来解释的现象有②④.
故选:C.
5.C
【分析】本题主要考查从不同方向看几何体,从左看,注意题目和图形给定的区别.
【详解】解:从左面看到的几何体的形状图有两列,第一列有两个正方体,第二列有一个,
故选:C.
6.C
【分析】本题考查的是抽样调查和全面调查的区别,一般来说,对于具有破坏性的调查无法进行全面调查,全面调查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用全面调查.根据全面调查的特点求解即可.
【详解】解:A、调查南宁市中学生每天的阅读时间,适合用抽样调查,故选项不符合题意;
B、调查全国中学生对网络安全知识的了解程度,适合用抽样调查,故选项不符合题意;
C、对发射卫星的运载火箭零部件质量的检查,适合用全面调查,故选项符合题意;
D、调查某品牌手机电池的使用寿命,适合用抽样调查,故选项不符合题意;
故选:C.
7.C
【分析】本题主要考查在数轴上表示有理数,数轴上两点之间的距离,以及相反数的意义.由点C对应的有理数是a,,根据两点之间的距离求出点A,然后利用相反数的意义即可求解.
【详解】解:∵点C对应的有理数是a,,
∴点A对应的有理数为:,
∵,
∴A,B是一对相反数.
∴点B为,
故选:C.
8.D
【分析】选项用“”减去其它两种方式所占百分比即可判断,选项用的人数除以判断即可,选项用样本容量乘判断即可,选项用样本估计总体判断即可.
【详解】、“其它”的占比:,此选项结论错误,不符合题意,排除;
、本次抽样调查的样本容量:,此选项结论错误,不符合题意,排除;
、样本中公共交通出行的有:,此选项结论错误,不符合题意,排除;
、(万人),此选项结论正确,符合题意;
故选:.
【点睛】此题考查了条形统计图和扇形统计图,总体,个体,样本容量,样本估计总体的思想等知识,解题的关键是读懂图象信息.
9.B
【分析】本题考查了图形类规律探索,正确归纳类推出一般规律是解题关键.先根据前4个图形发现规律,再根据一般规律求解即可得.
【详解】解:由题意可知,第1个图形中正方形的个数是个,
第2个图形中正方形的个数是个,
第3个图形中正方形的个数是个,
第4个图形中正方形的个数是个,
归纳类推得:第个图形中正方形的个数是个,(为正整数),
则第100个图形中正方形的个数是个,
故选:B.
10.B
【分析】先根据绝对值和完全平方的非负性,及“两个非负数的和为0,则每一个数都为0”求出x、y的值,再代入求值即可.掌握“两个非负数的和为0,则每一个数都为0”这一性质是解题的关键.
【详解】且,,
,,,
,,
,,
.
故选:B.
11.
【分析】本题考查了相反数、倒数、代数式求值;熟练掌握“只有符号不同的两个数是互为相反数;互为倒数的两数乘积为”是解题的关键.
根据相反数的定义,倒数的定义,求出,,代入计算即可.
【详解】解:根据相反数和倒数的定义得:
∵,,
∴.
故答案为:.
12.24
【分析】本题考查了认识立体图形.先确定是几棱柱,再求解.
【详解】解:∵一个棱柱有10个面,
∴该棱柱为八棱柱,
∴这个棱柱有24条棱,
故答案为:24.
13.3
【分析】本题考查了同类项的定义,根据同类项的定义得,进而可求解,熟记:“所含字母相同,并且相同字母的指数也分别相等的项叫做同类项”是解题的关键.
【详解】解:依题意得:,
解得:,
故答案为:3.
14.2049300
【分析】本题考查了角的概念和规律探索,解题的关键在于推导得出一般性规律.根据角的个数,推导出一般性规律,进而求解即可.
【详解】解:由题意知画1条射线,图中共有个角,
画2条射线,图中共有个角,
画3条射线,图中共有个角,
由此推导出一般性规律:画条射线,图中共有个角,
∴当时,,
故答案为:2049300.
15.2
【分析】本题主要考查了数轴上两点的距离计算,先求出,再根据题意可得,则.
【详解】解:∵点A、B、C是数轴上从左到右排列的三个点,分别对应的数为,b,8,
∴,
∵刻度尺上的数字0对齐数轴上的点A,发现点B对应刻度,点C对齐刻度,
∴,
∴,
故答案为:2.
16.
【分析】根据线段比例,设设,则,列出一元一次方程求解即可.本题考查两点间的距离,弄清楚线段之间的数量关系是关键.
【详解】解:∵,
∴设,
则,
∵点P是的中点,
∴,
∴,
∵,
∴,
解得,
∴.
故答案为:.
17.甲
【分析】根据统计图中所反映的数据的变化情况进行判断.
【详解】解:甲组的成绩变化从70到90,乙组的成绩变化是从70到85,所以甲组进步更大.
故答案为:甲.
【点睛】考查折线统计图的意义和制作方法,同时注意折线统计图容易给人造成错觉的原因,要正确的识别统计图,得出客观的结论.
18.2或/或2
【分析】本题主要考查了相反数的定义,倒数的定义,数轴上两点之间的距离,解题的关键是掌握相反数相加得0,乘积为1的两个数互为倒数,以及数轴上两点之间距离的表示方法.根据题意得出,,或,将其代入求解即可.
【详解】解:∵a、b互为相反数,
∴,
∵c、d互为倒数,
∴,
∵数轴上表示m的点与表示的点距离5个单位长度,
∴或,
∴,
或,
故答案为:2或.
19.(1);
(2).
【分析】本题考查了解一元一次方程,能正确根据等式的性质进行变形是解此题的关键.
(1)移项,合并同类项,系数化成1即可;
(2)去分母,去括号,移项,合并同类项,系数化成1即可.
【详解】(1)解:,
移项,得,
合并同类项,得,
系数化成1,得;
(2)解:
去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化成1,得;
20.(1)
(2)
【分析】本题考查的是有理数的混合运算,掌握混合运算的运算顺序是解本题的关键;
(1)先化为省略加号的和的形式,再计算即可;
(2)先计算乘方运算,再计算乘除运算,最后计算加减运算即可.
【详解】(1)解:
;
(2)
;
21.(1)见解析
(2)见解析
(3)见解析
【分析】本题主要考查了线段、直线、射线的作图,
(1)根据直线的定义,作图即可;
(2)根据射线的定义,结合(1)的结论,作图即可;
(3)延长,然后以点为圆心,以长为半径,在的延长线上,截取,即.
【详解】(1)解:如图,直线为所求,
(2)如图所示,
(3)如图所示,
22.(1);
(2)①;;②当逐渐增大时,纸盒容积的变化情况:先随着的增大而增大,后随着的增大而减小,
【分析】本题主要考查了列代数式,一元一次方程的应用,代数式求值:
(1)根据正方形的面积公式结合图形进行计算即可;
(2)①利用纸盒的容积的公式求出的值,然后把,代入进行计算即可,②通过计算,2,3,4,5,6,7,8,9时,纸盒的容积即可解答;
【详解】(1)解:由题意得,这个纸盒的底面积是,高是,
故答案为:;;
(2)解:∵当时,纸盒容积为,
∴,
解得,
∴,
故答案为:;;
②当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
当时,纸盒容积,
∴当逐渐增大时,纸盒容积的变化情况:先随着的增大而增大,后随着的增大而减小.
23.(1)
(2)
【分析】本题考查了整式的加减运算,以及化简求值,相反数的定义
(1)先把表示出来,再与进行减法运算,合并同类项,即可作答.
(2)依题意,,,代入,即可作答.
【详解】(1)解:∵,,
∴
;
(2)解:由题意知,,
原式.
24.(1);
(2)图见详解;
(3),;
【分析】本题考查求样本容量,补全直方图,求扇形同统计图的圆心角度数,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)根据的频数及占比直接求解即可得到答案;
(2)结合(1)求出和的量,补全图形即可得到答案;
(3)利用乘以占比即可得到答案.
【详解】(1)解:由图像可得,
此次共调查了:(人),
故答案为:;
(2)解:由图像及(1)得,
的人数为:(人),
的人数为:(人),
∴频数分布直方图如图所示,
;
(3)解:由图形及(2)得,
组的圆心角为:,
组的圆心角为:.
答案第1页,共2页
答案第1页,共2页
同课章节目录
