江苏省盐城市东台市2023-2024学年上学期九年级期末数学试题(含答案及评分标准)
文档属性
| 名称 | 江苏省盐城市东台市2023-2024学年上学期九年级期末数学试题(含答案及评分标准) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 00:00:00 | ||
图片预览

文档简介
2023-2024学年度第一学期期末学业水平考试
九年级数学
(试卷分值150分,考试时间120分钟)
注意事项:
1.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.
2.答题前,务必将自己的学校、班级、姓名、座位号填写在答题卡上相应位置.
一、选择题(本大题共有8小题,每小题3分,共24分、在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.一元二次方程的解为( )
A.=3 B.=4 C.=-4 D.
2.⊙O的半径为3,若点Р在⊙O外,点Р到圆心的距离为d,则d满足的条件为( )
A.d>3 B.d=3 C.03.甲、乙两地相距1600米,在地图上,用8厘米表示这两地的距离,那么这幅地图的比例尺是( )
A.1:200 B.1:20000 C.20000:1 D.1:40000
4.某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为188cm的队员换下场上身高为194cm的队员,与换人前相比,场上队员的身高( )
A.平均数变小,方差变小 B.平均数变小,方差变大
C.平均数变大,方差变小 D.平均数变大,方差变大
5.下列命题中是真命题的是( )
A.有一个角相等的直角三角形都相似 B.有一个角相等的等腰三角形都相似
C.有一个角是120°的等腰三角形都相似 D.两边成比例且有一角相等的三角形都相似
6.如图,△ABC的顶点都在正方形网格的格点上,则tan∠ACB的值为( )
A. B. C. D.
7.若关于的一元二次方程有实数根,则m的值不可能是( )
A.2 B.1 C.-1 D.-2
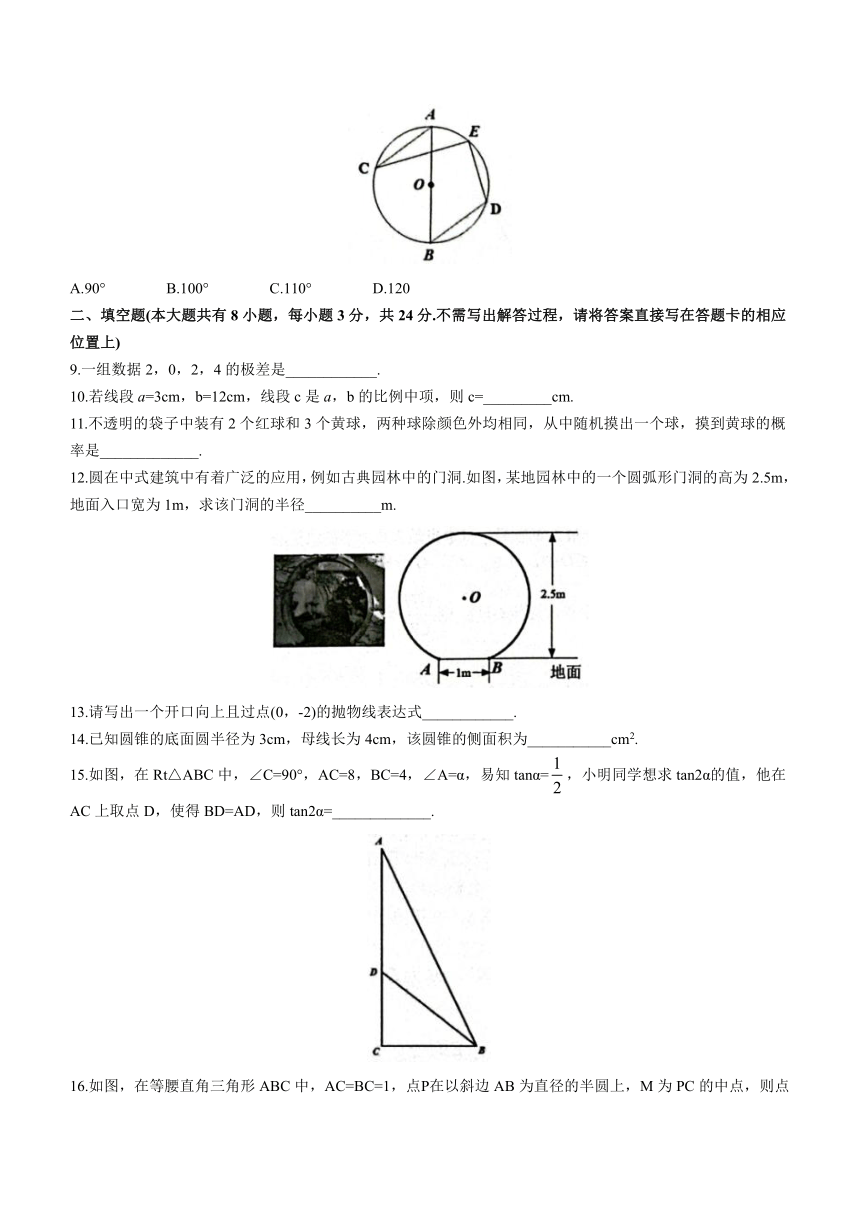
8.如图,AB是⊙O的直径,点C、D、E在⊙O上,若∠ACE=20°,则∠BDE的度数为( )
A.90° B.100° C.110° D.120
二、填空题(本大题共有8小题,每小题3分,共24分.不需写出解答过程,请将答案直接写在答题卡的相应位置上)
9.一组数据2,0,2,4的极差是____________.
10.若线段a=3cm,b=12cm,线段c是a,b的比例中项,则c=_________cm.
11.不透明的袋子中装有2个红球和3个黄球,两种球除颜色外均相同,从中随机摸出一个球,摸到黄球的概率是_____________.
12.圆在中式建筑中有着广泛的应用,例如古典园林中的门洞.如图,某地园林中的一个圆弧形门洞的高为2.5m,地面入口宽为1m,求该门洞的半径__________m.
13.请写出一个开口向上且过点(0,-2)的抛物线表达式____________.
14.已知圆锥的底面圆半径为3cm,母线长为4cm,该圆锥的侧面积为___________cm2.
15.如图,在Rt△ABC中,∠C=90°,AC=8,BC=4,∠A=α,易知tanα=,小明同学想求tan2α的值,他在AC上取点D,使得BD=AD,则tan2α=_____________.
16.如图,在等腰直角三角形ABC中,AC=BC=1,点Р在以斜边AB为直径的半圆上,M为PC的中点,则点Р沿半圆由点A运动至点B的过程中,线段BM的最小值为____________.
三、解答题(本大题共有11小题,共102分.请在答题卡指定区域内作答,解答时应写出文字说明、推理过程或演算步骤)
17.(本题满分6分)计算.
18.(本题满分6分)解方程.
19.(本题满分8分)为了解“双减”后学生每天完成课外作业所需时长的情况,某市从甲、乙两所学校各随机抽取50名学生进行调查,获取他们每天完成课外作业所需时长(单位t分钟)的数据,并对数据进行了整理、描述和分析,下面给出了部分信息.
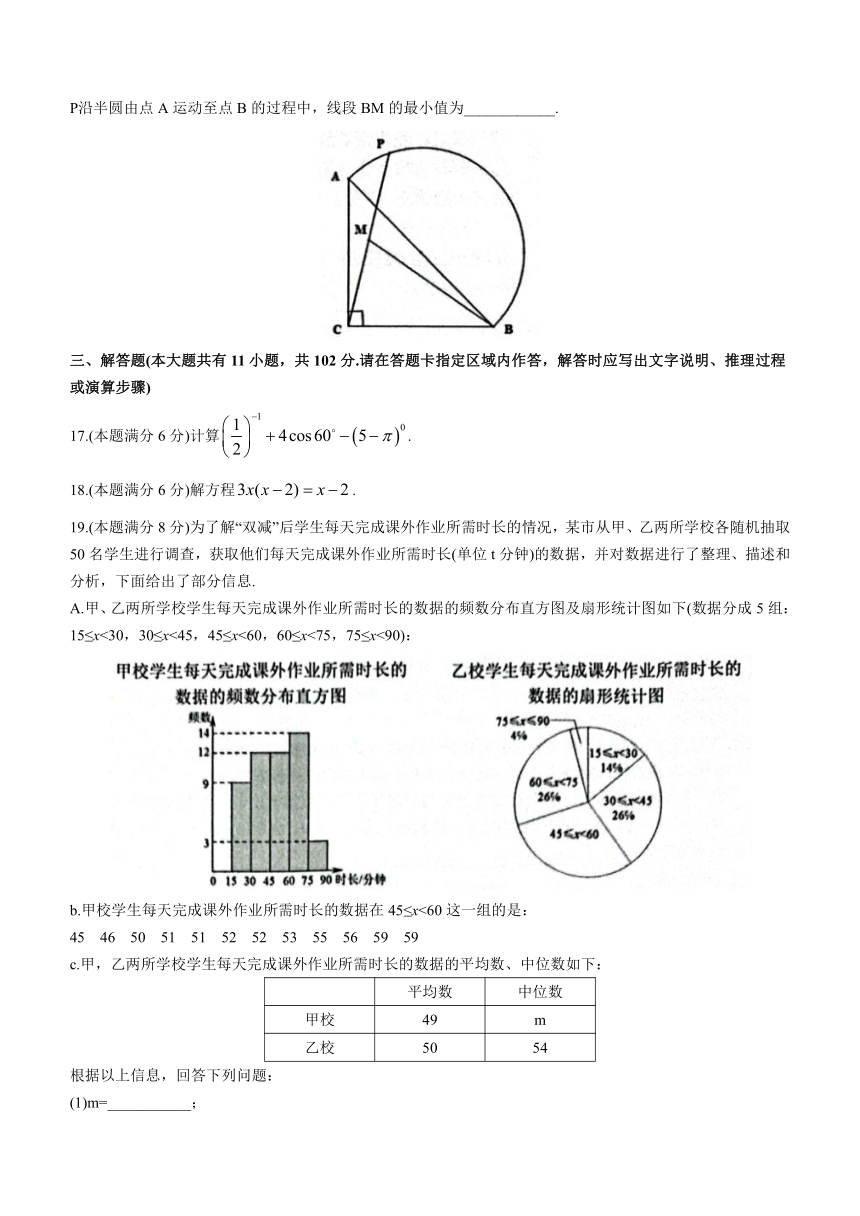
A.甲、乙两所学校学生每天完成课外作业所需时长的数据的频数分布直方图及扇形统计图如下(数据分成5组:15≤x<30,30≤x<45,45≤x<60,60≤x<75,75≤x<90):
b.甲校学生每天完成课外作业所需时长的数据在45≤x<60这一组的是:
45 46 50 51 51 52 52 53 55 56 59 59
c.甲,乙两所学校学生每天完成课外作业所需时长的数据的平均数、中位数如下:
平均数 中位数
甲校 49 m
乙校 50 54
根据以上信息,回答下列问题:
(1)m=___________;
(2)乙校学生每天完成课外作业所需时长的数据的扇形统计图中表示45≤x<60这组数据的扇形圆心角的度数是__________°;
(3)小明每天完成课外作业所需时长为53分钟,在与他同校被调查的学生中,有一半以上的学生每天完成课外作业所需时长都超过了小明,那么小明是__________校学生;
(4)如果甲,乙两所学校各有400人,估计这两所学校每天完成课外作业所需时长低于60分钟的学生共有_________人.
20.(本题满分8分)已知二次函数.
(1)求二次函数图像的顶点坐标;
(2)在平面直角坐标系xOy中,画出二次函数的图像;
(3)当121.(本题满分8分)现如今,“垃圾分类”意识已深入人心,某小区有四个不同的垃圾分类投放桶,分别写着:有害垃圾、易腐垃圾、其他垃圾、可回收垃圾,其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“可回收垃圾”的概率;
(2)求小丽投放的两袋垃圾不同类的概率(画树状图或列表求解).
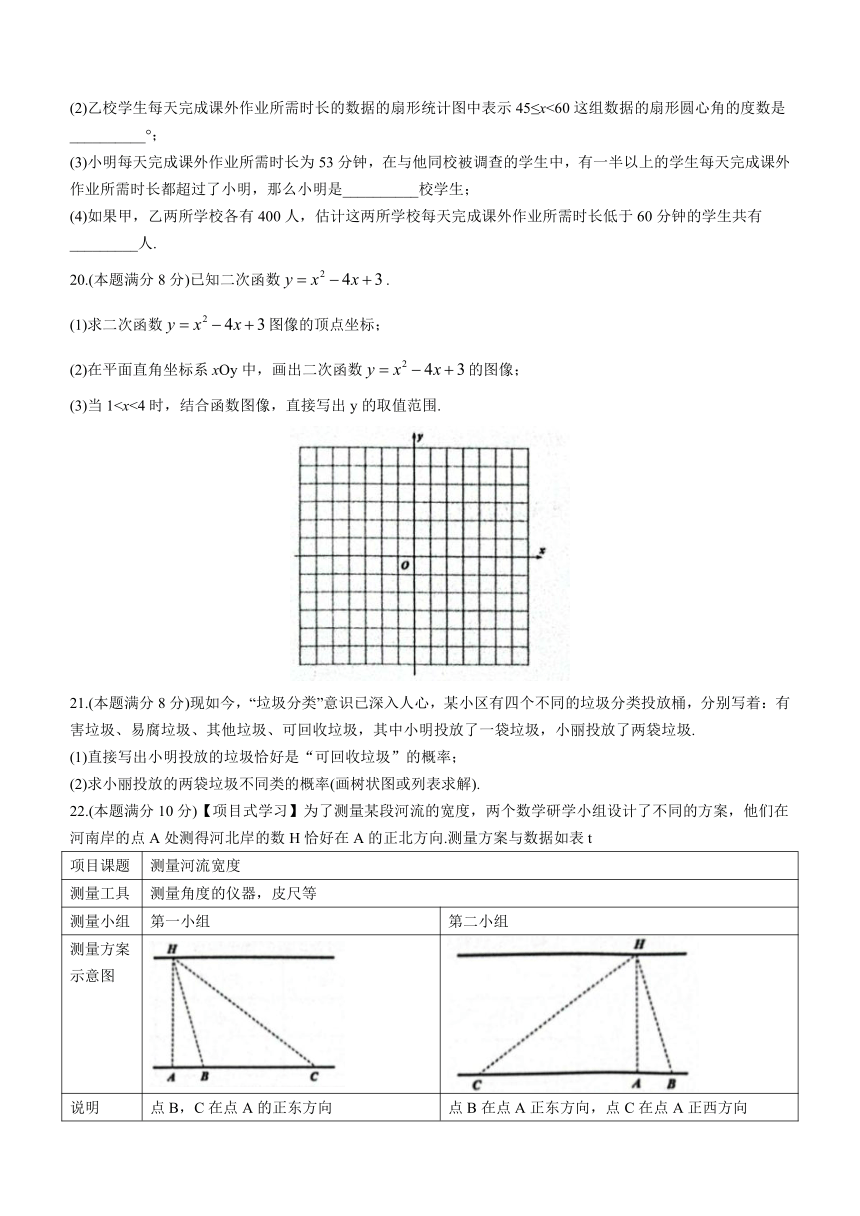
22.(本题满分10分)【项目式学习】为了测量某段河流的宽度,两个数学研学小组设计了不同的方案,他们在河南岸的点A处测得河北岸的数H恰好在A的正北方向.测量方案与数据如表t
项目课题 测量河流宽度
测量工具 测量角度的仪器,皮尺等
测量小组 第一小组 第二小组
测量方案 示意图
说明 点B,C在点A的正东方向 点B在点A正东方向,点C在点A正西方向
数据 BC=200m,∠ABH=74°,∠ACH=37° BC=311m,∠ABH=74°,∠ACH=37°
请选择其中一个方案及其数据:
(1)求么AHB的度数;
(2)求出河宽(精确到1m).
参考数据:sin74°≈0.96,sin37°≈0.60,tan74≈3.50,tan37°≈0.75
23.(本题满分10分)戴口罩能有效阻断呼吸道病毒的传播.某商家对一款成本价为每盒50元的医用口罩进行销售,如果按每盒70元销售,每天可卖出20盒;通过市场调查发现,每盒口罩售价每降低1元,则日销售量增加2盒.
(1)若每盒售价降低x元,则日销量可表示为________盒,每盒口罩的利润为_________元.
(2)若日利润保持不变,商家想尽快销售完该款口罩,每盒售价应定为多少元
(3)当每盒售价定为多少元时,商家可以获得最大日利润 并求出最大日利润.
24.(本题满分10分)如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线,与BC交于点E,与AB的延长线交于点F.
(1)求证:DF上BC;
(2)若B是OF的中点,AD=,求出图中阴影部分的面积
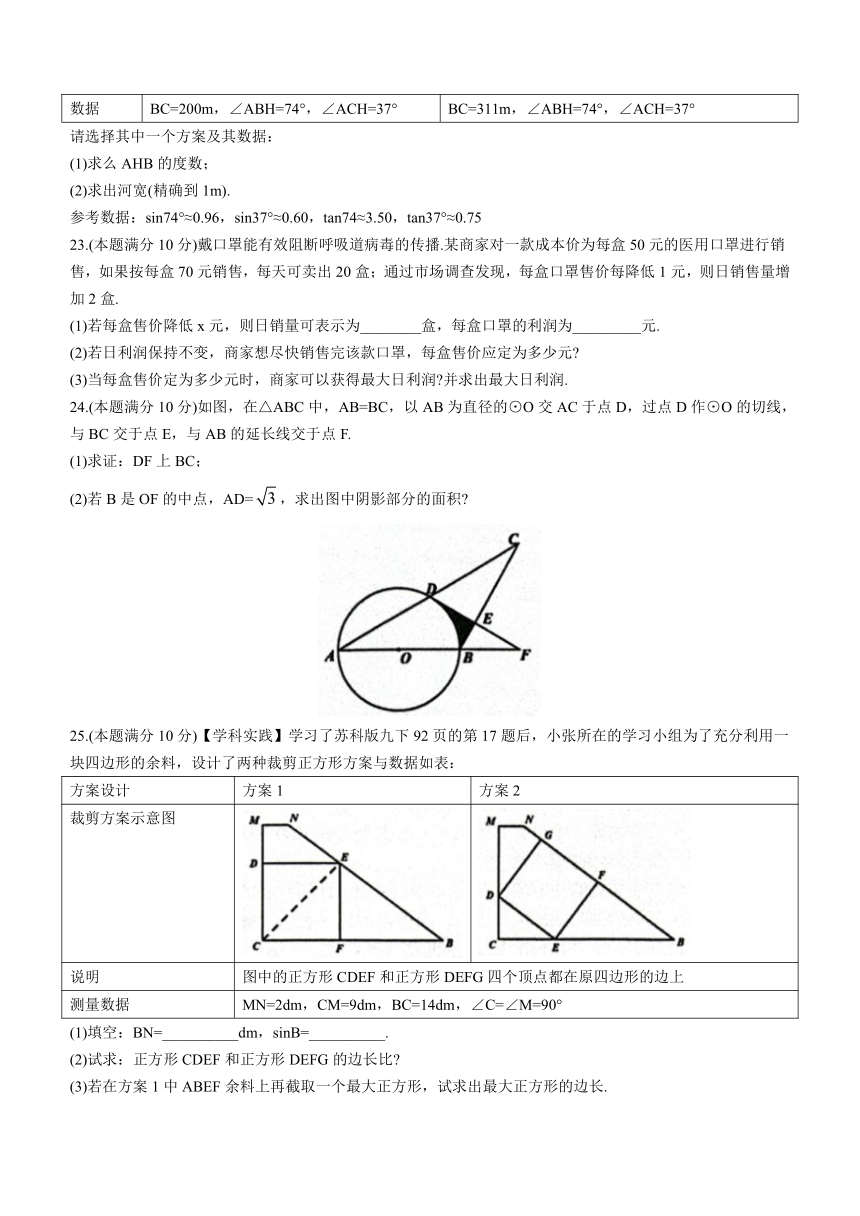
25.(本题满分10分)【学科实践】学习了苏科版九下92页的第17题后,小张所在的学习小组为了充分利用一块四边形的余料,设计了两种裁剪正方形方案与数据如表:
方案设计 方案1 方案2
裁剪方案示意图
说明 图中的正方形CDEF和正方形DEFG四个顶点都在原四边形的边上
测量数据 MN=2dm,CM=9dm,BC=14dm,∠C=∠M=90°
(1)填空:BN=__________dm,sinB=__________.
(2)试求:正方形CDEF和正方形DEFG的边长比
(3)若在方案1中ABEF余料上再截取一个最大正方形,试求出最大正方形的边长.
26.(本题满分12分)如图1,在正方形ABCD中,点E、F、G分别为边BC、AB、AD的中点,连接EF、DF,H为DF的中点,连接GH,则.
(1)将△BEF绕点B顺时针旋转90°,连接EC﹐得到图2,此时是否仍然成立 说明理由.
(2)若四边形ABCD为矩形,其他条件不变,AB=2,BC=3,则=_________;
(3)若四边形ABCD为矩形,将ABEF绕点B顺时针旋转β(0°<β<180°),其他条件不变,如图4,若AB=m,BC=n,则=___________.(用m、n表示)
(4)在图4中,当旋转角β为90°时,将ADGH沿GH翻折至如图5所示,得AKGH,若点K刚好与点F重合,则此时矩形ABCD的边长AB与BC满足什么关系 请说明理由.
27.(本题满分14分)如图1,二次函数的图像与x轴交于A、B(2,0)两点,与y轴交于点C(0,6),点P为该图像上一动点,连接AC、BC.
(1)求二次函数解析式;
(2)直接写出LACB的度数;
(3)当∠ABP=∠ACB时,求点Р坐标;
(4)如图2,在(3)的条件下,平行于BP动直线1与该图像交于D、E两点(直线l与BP不重合),连接PD、BE,直线PD与BE是否在y轴上交于同一点,请说明理由.
学生学业质量调查分析与反馈
九年级数学参考答案
一、选择题(每题3分,共24分)
题号 1 2 3 4 5 6 7 8
答案 D A B A C D A C
二、填空题(每题3分,计24分)
9.4;10.6;11.0.6(或);12.1.3;13.(符合即可);14.;15.;16.
三、解答题(本大题共11题,共102分)
17、解:原式=2+4×-1................................(2分)
=2+2-1.................................(4分)
=3.................................(6分)
18、解:.................................(2分)
,................................(4分)
,.................................(6分)
19、解:(1)51..................................(2分)
(2)108..................................(4分)
(3)乙..................................(6分)
(4)544..................................(8分)
20、(1)
顶点坐标为(2,-1)..................................(2分)
(2)函数图像如图所示:(如通过列表或计算给出了与坐标轴的交点,给1分)
..................................(5分)
(3)(如无等于号扣1分).................(8分)
21、解:(1).................(3分)
(2)解法一:画树状图设有害垃圾为A,易腐垃圾为B,其他垃圾为C,可回收垃圾为D
共有16种等可能的结果,其中小丽投放的两袋垃圾不同类的结果有12种.................(6分)
∴P(小丽投放的两袋垃圾不同类)=.................(8分)
解法二:设有害垃圾为A,易腐垃圾为B,其他垃圾为C,可回收垃圾为D列表如下:
A B C D
A A(A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中小丽投放的两袋垃圾不同类的结果有12种....................(6分)
∴P(小丽投放的两袋垃圾不同类)=....................(8分)
22、解:(1)由题意可知HA⊥AC,在Rt△ABH中,∠AHB=90°-∠ABH=16°..................(5分)
(2)如选第一组则求解如下:∵∠ABH是∠HBC的外角
∴∠ABH=∠C+∠BHC
∴∠BHC=∠ABH-∠C=37°
∴∠C=∠BHC
∴BH=CH=200
在Rt△ABH∠tan在中,
AH=200×0.96=192(m)
答:河宽为192米...........................(10分)
如选第二组则求解如下:
设AH为a,在Rt△ACH中,,,
在Rt△ABH中,,,
,(m)
答:河宽为192米............................(10分)
23、(1),............................(4分)
(2)解:设每盒售价降低x元,
解得,
∵商家想尽快销售完该口罩,即销售量要大
∴x取10,
答:每盒售价应定为60元.............................(7分)
(3)设商家可以获得日利润为y元,
...................................(9分)
由二次函数性质可知,时,y取最大值,y=450(元)
70-5=65(元)
答:当每盒售价定为65元时,商家可以获得最大日利润450元..............................................(10分)
24、(1)证明:连接OD,
∵DF为⊙O的切线
∴DF⊥OD
∵AB=AC
∴∠A=∠C
∵OA=OD
∴∠A=∠ADO
∴∠C=∠ADO
∴OD∥BC
∴DF⊥BC...................................(5分)
(2)证明:如图,连接BD,
∵B为OF的中点且∠ODF=90°,
∴BD=OB,△BOD是等边三角形
在Rt△ABD中,,
在Rt△BDE中∠BDE=90°-60°=30°
∴BE=BDsin30°=,DE=BD·cos30°=,
∴
答:图中阴影部分的面积为...........................(10分)
25、(1)BN=15,sinB=...........................(4分)
(2)设正方形CDEF和正方形DEFG的边长分别为a,b.
由(1)知sinB=,则tanB=
如方案1图,在Rt△BEF中,CF=EF=
∴
∴=6...........................(5分)
如方案2图,∵四边形DEFG是正方形
∴DE∥BN,DE=EF=b
∴∠CED=∠B
∴sin∠CED=sinB=
在Rt△CDE中
sin∠CED=,则cos∠CED=
∴CE=
在Rt△CDE中,,EF=b
.......................(6分)
∴
∴正方形CDEF和正方形DEFG的边长比........................(7分)
(3)由(2)可知,当正方形的两边在Rt△BEF的两条直角边上时正方形最大
如图,设正方形FGHK,则FK=HK
在Rt△BEF中EF=6,BF=8,tanB=
在Rt△BHK中,
∴
∴
答:在方案1中 BEF余料上再截取一个最大正方形,最大正方形的边长为dm...........................(10分)
26、(1)连接AF,在△ABF和△CBE中
∴△ABF≌△CBE(SAS)
∴AF=CE
∵G、H分别是AD、DF的中点
∴GH是△ADF的中位线
∴
∴.........................(4分)
(2).........................(6分)
(3).........................(8分)
(4)
.........................(9分)
当K与F重合时,GH⊥DF,则AF⊥DF
易得△ABF∽△FCD
∴
设AB=m,则
∴FC=2m
∴...........................(12分)
27、(1)将B(2,0),C(0,6)代入
解得
∴二次函数解析式为...........................(4分)
(2)∠ACB=45°...........................(6分)
(3)当∠ABP=∠ACB=45°时易得或
由得,(舍去)
由得,(舍去)
∴点P坐标为(-2,4)或(-4,-6)...........................(10分)
(4)设D,E,
易得直线BP解析式为,
设直线DE解析式为,
则
得
∴,
∴
∴E
易得直线PD解析式为
直线BE解析式为
∴直线PD与直线BE在y轴上交于同一点...........................(14分)
【解答题有其他思路并且正确完成的参照给分】
九年级数学
(试卷分值150分,考试时间120分钟)
注意事项:
1.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.
2.答题前,务必将自己的学校、班级、姓名、座位号填写在答题卡上相应位置.
一、选择题(本大题共有8小题,每小题3分,共24分、在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.一元二次方程的解为( )
A.=3 B.=4 C.=-4 D.
2.⊙O的半径为3,若点Р在⊙O外,点Р到圆心的距离为d,则d满足的条件为( )
A.d>3 B.d=3 C.0
A.1:200 B.1:20000 C.20000:1 D.1:40000
4.某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为188cm的队员换下场上身高为194cm的队员,与换人前相比,场上队员的身高( )
A.平均数变小,方差变小 B.平均数变小,方差变大
C.平均数变大,方差变小 D.平均数变大,方差变大
5.下列命题中是真命题的是( )
A.有一个角相等的直角三角形都相似 B.有一个角相等的等腰三角形都相似
C.有一个角是120°的等腰三角形都相似 D.两边成比例且有一角相等的三角形都相似
6.如图,△ABC的顶点都在正方形网格的格点上,则tan∠ACB的值为( )
A. B. C. D.
7.若关于的一元二次方程有实数根,则m的值不可能是( )
A.2 B.1 C.-1 D.-2
8.如图,AB是⊙O的直径,点C、D、E在⊙O上,若∠ACE=20°,则∠BDE的度数为( )
A.90° B.100° C.110° D.120
二、填空题(本大题共有8小题,每小题3分,共24分.不需写出解答过程,请将答案直接写在答题卡的相应位置上)
9.一组数据2,0,2,4的极差是____________.
10.若线段a=3cm,b=12cm,线段c是a,b的比例中项,则c=_________cm.
11.不透明的袋子中装有2个红球和3个黄球,两种球除颜色外均相同,从中随机摸出一个球,摸到黄球的概率是_____________.
12.圆在中式建筑中有着广泛的应用,例如古典园林中的门洞.如图,某地园林中的一个圆弧形门洞的高为2.5m,地面入口宽为1m,求该门洞的半径__________m.
13.请写出一个开口向上且过点(0,-2)的抛物线表达式____________.
14.已知圆锥的底面圆半径为3cm,母线长为4cm,该圆锥的侧面积为___________cm2.
15.如图,在Rt△ABC中,∠C=90°,AC=8,BC=4,∠A=α,易知tanα=,小明同学想求tan2α的值,他在AC上取点D,使得BD=AD,则tan2α=_____________.
16.如图,在等腰直角三角形ABC中,AC=BC=1,点Р在以斜边AB为直径的半圆上,M为PC的中点,则点Р沿半圆由点A运动至点B的过程中,线段BM的最小值为____________.
三、解答题(本大题共有11小题,共102分.请在答题卡指定区域内作答,解答时应写出文字说明、推理过程或演算步骤)
17.(本题满分6分)计算.
18.(本题满分6分)解方程.
19.(本题满分8分)为了解“双减”后学生每天完成课外作业所需时长的情况,某市从甲、乙两所学校各随机抽取50名学生进行调查,获取他们每天完成课外作业所需时长(单位t分钟)的数据,并对数据进行了整理、描述和分析,下面给出了部分信息.
A.甲、乙两所学校学生每天完成课外作业所需时长的数据的频数分布直方图及扇形统计图如下(数据分成5组:15≤x<30,30≤x<45,45≤x<60,60≤x<75,75≤x<90):
b.甲校学生每天完成课外作业所需时长的数据在45≤x<60这一组的是:
45 46 50 51 51 52 52 53 55 56 59 59
c.甲,乙两所学校学生每天完成课外作业所需时长的数据的平均数、中位数如下:
平均数 中位数
甲校 49 m
乙校 50 54
根据以上信息,回答下列问题:
(1)m=___________;
(2)乙校学生每天完成课外作业所需时长的数据的扇形统计图中表示45≤x<60这组数据的扇形圆心角的度数是__________°;
(3)小明每天完成课外作业所需时长为53分钟,在与他同校被调查的学生中,有一半以上的学生每天完成课外作业所需时长都超过了小明,那么小明是__________校学生;
(4)如果甲,乙两所学校各有400人,估计这两所学校每天完成课外作业所需时长低于60分钟的学生共有_________人.
20.(本题满分8分)已知二次函数.
(1)求二次函数图像的顶点坐标;
(2)在平面直角坐标系xOy中,画出二次函数的图像;
(3)当1
(1)直接写出小明投放的垃圾恰好是“可回收垃圾”的概率;
(2)求小丽投放的两袋垃圾不同类的概率(画树状图或列表求解).
22.(本题满分10分)【项目式学习】为了测量某段河流的宽度,两个数学研学小组设计了不同的方案,他们在河南岸的点A处测得河北岸的数H恰好在A的正北方向.测量方案与数据如表t
项目课题 测量河流宽度
测量工具 测量角度的仪器,皮尺等
测量小组 第一小组 第二小组
测量方案 示意图
说明 点B,C在点A的正东方向 点B在点A正东方向,点C在点A正西方向
数据 BC=200m,∠ABH=74°,∠ACH=37° BC=311m,∠ABH=74°,∠ACH=37°
请选择其中一个方案及其数据:
(1)求么AHB的度数;
(2)求出河宽(精确到1m).
参考数据:sin74°≈0.96,sin37°≈0.60,tan74≈3.50,tan37°≈0.75
23.(本题满分10分)戴口罩能有效阻断呼吸道病毒的传播.某商家对一款成本价为每盒50元的医用口罩进行销售,如果按每盒70元销售,每天可卖出20盒;通过市场调查发现,每盒口罩售价每降低1元,则日销售量增加2盒.
(1)若每盒售价降低x元,则日销量可表示为________盒,每盒口罩的利润为_________元.
(2)若日利润保持不变,商家想尽快销售完该款口罩,每盒售价应定为多少元
(3)当每盒售价定为多少元时,商家可以获得最大日利润 并求出最大日利润.
24.(本题满分10分)如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线,与BC交于点E,与AB的延长线交于点F.
(1)求证:DF上BC;
(2)若B是OF的中点,AD=,求出图中阴影部分的面积
25.(本题满分10分)【学科实践】学习了苏科版九下92页的第17题后,小张所在的学习小组为了充分利用一块四边形的余料,设计了两种裁剪正方形方案与数据如表:
方案设计 方案1 方案2
裁剪方案示意图
说明 图中的正方形CDEF和正方形DEFG四个顶点都在原四边形的边上
测量数据 MN=2dm,CM=9dm,BC=14dm,∠C=∠M=90°
(1)填空:BN=__________dm,sinB=__________.
(2)试求:正方形CDEF和正方形DEFG的边长比
(3)若在方案1中ABEF余料上再截取一个最大正方形,试求出最大正方形的边长.
26.(本题满分12分)如图1,在正方形ABCD中,点E、F、G分别为边BC、AB、AD的中点,连接EF、DF,H为DF的中点,连接GH,则.
(1)将△BEF绕点B顺时针旋转90°,连接EC﹐得到图2,此时是否仍然成立 说明理由.
(2)若四边形ABCD为矩形,其他条件不变,AB=2,BC=3,则=_________;
(3)若四边形ABCD为矩形,将ABEF绕点B顺时针旋转β(0°<β<180°),其他条件不变,如图4,若AB=m,BC=n,则=___________.(用m、n表示)
(4)在图4中,当旋转角β为90°时,将ADGH沿GH翻折至如图5所示,得AKGH,若点K刚好与点F重合,则此时矩形ABCD的边长AB与BC满足什么关系 请说明理由.
27.(本题满分14分)如图1,二次函数的图像与x轴交于A、B(2,0)两点,与y轴交于点C(0,6),点P为该图像上一动点,连接AC、BC.
(1)求二次函数解析式;
(2)直接写出LACB的度数;
(3)当∠ABP=∠ACB时,求点Р坐标;
(4)如图2,在(3)的条件下,平行于BP动直线1与该图像交于D、E两点(直线l与BP不重合),连接PD、BE,直线PD与BE是否在y轴上交于同一点,请说明理由.
学生学业质量调查分析与反馈
九年级数学参考答案
一、选择题(每题3分,共24分)
题号 1 2 3 4 5 6 7 8
答案 D A B A C D A C
二、填空题(每题3分,计24分)
9.4;10.6;11.0.6(或);12.1.3;13.(符合即可);14.;15.;16.
三、解答题(本大题共11题,共102分)
17、解:原式=2+4×-1................................(2分)
=2+2-1.................................(4分)
=3.................................(6分)
18、解:.................................(2分)
,................................(4分)
,.................................(6分)
19、解:(1)51..................................(2分)
(2)108..................................(4分)
(3)乙..................................(6分)
(4)544..................................(8分)
20、(1)
顶点坐标为(2,-1)..................................(2分)
(2)函数图像如图所示:(如通过列表或计算给出了与坐标轴的交点,给1分)
..................................(5分)
(3)(如无等于号扣1分).................(8分)
21、解:(1).................(3分)
(2)解法一:画树状图设有害垃圾为A,易腐垃圾为B,其他垃圾为C,可回收垃圾为D
共有16种等可能的结果,其中小丽投放的两袋垃圾不同类的结果有12种.................(6分)
∴P(小丽投放的两袋垃圾不同类)=.................(8分)
解法二:设有害垃圾为A,易腐垃圾为B,其他垃圾为C,可回收垃圾为D列表如下:
A B C D
A A(A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中小丽投放的两袋垃圾不同类的结果有12种....................(6分)
∴P(小丽投放的两袋垃圾不同类)=....................(8分)
22、解:(1)由题意可知HA⊥AC,在Rt△ABH中,∠AHB=90°-∠ABH=16°..................(5分)
(2)如选第一组则求解如下:∵∠ABH是∠HBC的外角
∴∠ABH=∠C+∠BHC
∴∠BHC=∠ABH-∠C=37°
∴∠C=∠BHC
∴BH=CH=200
在Rt△ABH∠tan在中,
AH=200×0.96=192(m)
答:河宽为192米...........................(10分)
如选第二组则求解如下:
设AH为a,在Rt△ACH中,,,
在Rt△ABH中,,,
,(m)
答:河宽为192米............................(10分)
23、(1),............................(4分)
(2)解:设每盒售价降低x元,
解得,
∵商家想尽快销售完该口罩,即销售量要大
∴x取10,
答:每盒售价应定为60元.............................(7分)
(3)设商家可以获得日利润为y元,
...................................(9分)
由二次函数性质可知,时,y取最大值,y=450(元)
70-5=65(元)
答:当每盒售价定为65元时,商家可以获得最大日利润450元..............................................(10分)
24、(1)证明:连接OD,
∵DF为⊙O的切线
∴DF⊥OD
∵AB=AC
∴∠A=∠C
∵OA=OD
∴∠A=∠ADO
∴∠C=∠ADO
∴OD∥BC
∴DF⊥BC...................................(5分)
(2)证明:如图,连接BD,
∵B为OF的中点且∠ODF=90°,
∴BD=OB,△BOD是等边三角形
在Rt△ABD中,,
在Rt△BDE中∠BDE=90°-60°=30°
∴BE=BDsin30°=,DE=BD·cos30°=,
∴
答:图中阴影部分的面积为...........................(10分)
25、(1)BN=15,sinB=...........................(4分)
(2)设正方形CDEF和正方形DEFG的边长分别为a,b.
由(1)知sinB=,则tanB=
如方案1图,在Rt△BEF中,CF=EF=
∴
∴=6...........................(5分)
如方案2图,∵四边形DEFG是正方形
∴DE∥BN,DE=EF=b
∴∠CED=∠B
∴sin∠CED=sinB=
在Rt△CDE中
sin∠CED=,则cos∠CED=
∴CE=
在Rt△CDE中,,EF=b
.......................(6分)
∴
∴正方形CDEF和正方形DEFG的边长比........................(7分)
(3)由(2)可知,当正方形的两边在Rt△BEF的两条直角边上时正方形最大
如图,设正方形FGHK,则FK=HK
在Rt△BEF中EF=6,BF=8,tanB=
在Rt△BHK中,
∴
∴
答:在方案1中 BEF余料上再截取一个最大正方形,最大正方形的边长为dm...........................(10分)
26、(1)连接AF,在△ABF和△CBE中
∴△ABF≌△CBE(SAS)
∴AF=CE
∵G、H分别是AD、DF的中点
∴GH是△ADF的中位线
∴
∴.........................(4分)
(2).........................(6分)
(3).........................(8分)
(4)
.........................(9分)
当K与F重合时,GH⊥DF,则AF⊥DF
易得△ABF∽△FCD
∴
设AB=m,则
∴FC=2m
∴...........................(12分)
27、(1)将B(2,0),C(0,6)代入
解得
∴二次函数解析式为...........................(4分)
(2)∠ACB=45°...........................(6分)
(3)当∠ABP=∠ACB=45°时易得或
由得,(舍去)
由得,(舍去)
∴点P坐标为(-2,4)或(-4,-6)...........................(10分)
(4)设D,E,
易得直线BP解析式为,
设直线DE解析式为,
则
得
∴,
∴
∴E
易得直线PD解析式为
直线BE解析式为
∴直线PD与直线BE在y轴上交于同一点...........................(14分)
【解答题有其他思路并且正确完成的参照给分】
同课章节目录
