第25章相似形单元复习题 (含解析)冀教版九年级数学上册
文档属性
| 名称 | 第25章相似形单元复习题 (含解析)冀教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 491.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 16:25:41 | ||
图片预览




文档简介
冀教版九年级数学上册第25章相似形单元复习题
一、单选题
1.如图,矩形ABCD中,点E为AB边中点,连接AC、DE交于点F,若的面积为4,则的面积为( )
A.3 B.4 C.6 D.8
2.一种数学课本的宽与长之比为黄金比,已知它的长是26cm,那么它的宽是( )cm。
A.+26 B.-26 C.+14 D.-13
3.下列命题中的真命题是( )
A.两个直角三角形都相似
B.若一个直角三角形的两条边和另一个直角三角形的两条边成比例,则这两个直角三角形相似
C.两个等腰三角形都相似
D.两个等腰直角三角形都相似
4.已知 ,则 的值为( )
A. B. C. D.
5.如图,l1 l2 l3,直线a,b与l1,l2,l3分别相交于A,B,C和D,E,F.若 ,DE=4,则EF的长为( )
A.10 B. C.12 D.14
6.已知 ,那么下列等式一定成立的是( )
A.x=2,y=3 B. C. D.
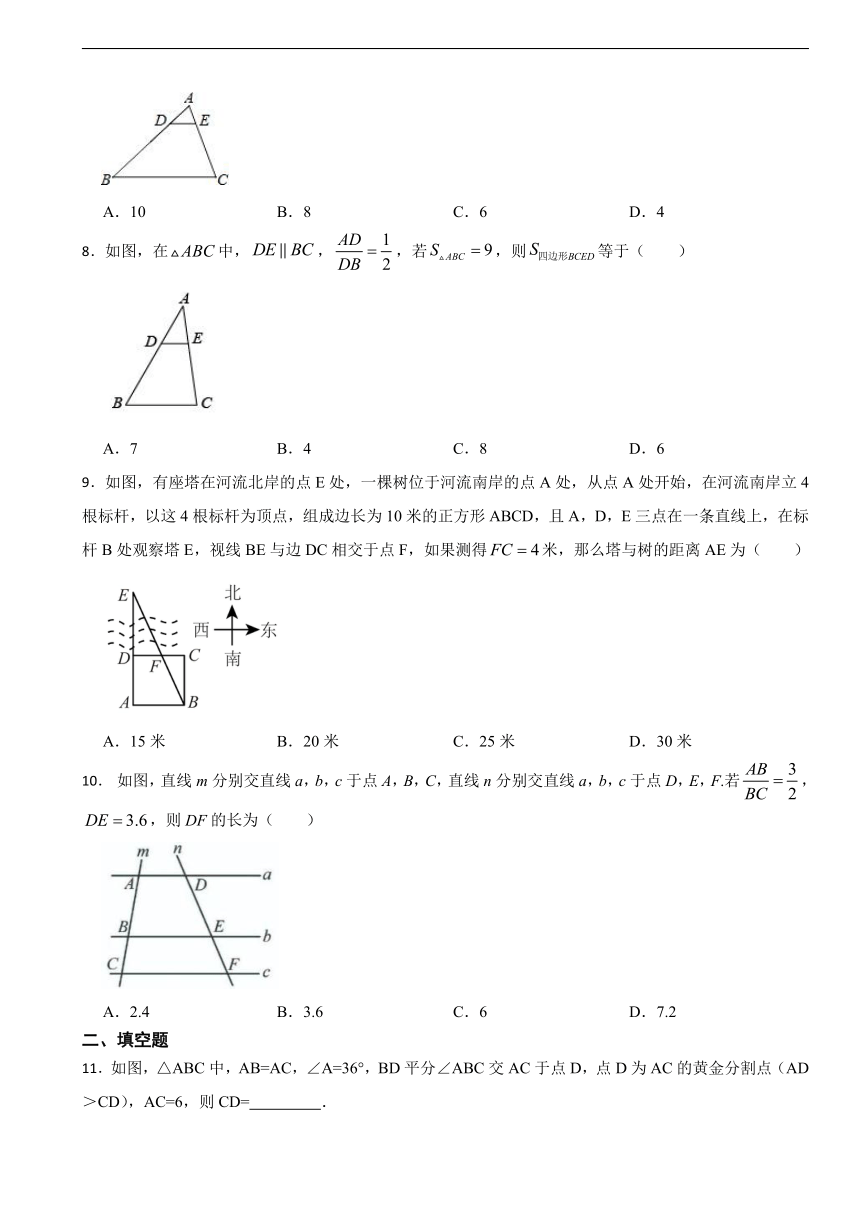
7.如图,D,E为△ABC的边AB,AC上的点,DE∥BC,若AD:DB=1:3,AE=2,则AC的长是( )
A.10 B.8 C.6 D.4
8.如图,在中,,,若,则等于( )
A.7 B.4 C.8 D.6
9.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形ABCD,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线BE与边DC相交于点F,如果测得米,那么塔与树的距离AE为( )
A.15米 B.20米 C.25米 D.30米
10. 如图,直线m分别交直线a,b,c于点A,B,C,直线n分别交直线a,b,c于点D,E,F.若,,则DF的长为( )
A.2.4 B.3.6 C.6 D.7.2
二、填空题
11.如图,△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,点D为AC的黄金分割点(AD>CD),AC=6,则CD= .
12.如图,EF为△ABC的中位线,△ABC的周长为12cm,则△AEF的周长为 cm.
13.如图,正方形纸片 的边长为12, 是边 上一点,连接 .折叠该纸片,使点 落在 上的 点,并使折痕经过点 ,得到折痕 ,点 在 上.若 ,则 的长为 .
14.如图,在矩形ABCD和矩形AEGH中,AD∶AB=AH∶AE=1∶2.则DH∶CG∶BE= .
三、解答题
15.如图,△ABC中,A、B两点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,求点B的横坐标.
16.如图,已知D为 内一点,E为 外一点,且 , .求证: .
17.在直角坐标系中,已知点A(﹣2,0),B(0,4),C(0,3),过点C作直线交x轴于点D,使得以D,O,C为顶点的三角形与△AOB相似,求点D的坐标.
18.如图,中有内接正方形DEFG,DE在BC边上,顶点G、F分别在AB、AC边上,,垂足为H,交GF于I.求证:.
四、综合题
19.已知,四边形 的两条对角相交于点 , .
(1)求证: .
(2)若 , ,求 的长.
20.在△ 中,已知 是 边的中点, 是△ 的重心,过 点的直线分别交 、 于点 、 .
(1)如图1,当 ∥ 时,求证: ;
(2)如图2,当 和 不平行,且点 、 分别在线段 、 上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
(3)如图3,当点 在 的延长线上或点 在 的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
21.如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.
22.已知:在Rt△ABC中,∠B=90°,BC=4cm,AB=8cm,D、E、F分别为AB、AC、BC边上的中点.若P为AB边上的一个动点,PQ∥BC,且交AC于点Q,以PQ为一边,在点A的异侧作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.
(1)如图,当AP=3cm时,求y的值;
(2)设AP=xcm,试用含x的代数式表示y(cm2);
(3)当y=2cm2时,试确定点P的位置.
23.已知平行四边形ABCD中,N是边BC上一点,延长DN、AB交于点Q,过A作AM⊥DN于点M,连接AN,则AD⊥AN.
(1)如图①,若tan∠ADM= ,MN=3,求BC的长;
(2)如图②,过点B作BH∥DQ交AN于点H,若AM=CN,求证:DM=BH+NH.
答案解析部分
1.【答案】A
【解析】【解答】解:∵四边形ABCD是矩形,
∴ABCD,AB=CD,
∴△AEF∽△CDF,
∵点E是AB中点,
∴CD=AB=2AE,
∴,
∵的面积为4,
∴△AEF的面积为1,
∴△ADF的面积为2,
∴的面积为3,
故答案为:A.
【分析】先证明△AEF∽△CDF,可得,再结合的面积为4,可得△AEF的面积为1,最后求出的面积为3即可。
2.【答案】D
【解析】【解答】解: ∵书的宽与长之比为黄金比,长为26cm,
∴它的宽=.
故答案为:D.
【分析】 根据黄金分割的定义得到书的宽与长之比为,得出它的宽为,即可得出答案.
3.【答案】D
【解析】【解答】解:A. 两个直角三角形不一定都相似,故A不符合题意;
B. 若一个直角三角形的两条边和另一个直角三角形的两条边成比例,则这两个直角三角形不一定相似,故B不符合题意;
C. 两个等腰三角形不一定都相似,故C不符合题意;
D.两个等腰直角三角形都相似,故D符合题意.
故答案为:D.
【分析】本题考查相似三角形的判定,根据相似三角形的判定方法逐项进行判断,即可求解.
4.【答案】A
【解析】【解答】∵ ,
设 ,则 ,
∴ ,
故答案为:A.
【分析】根据比例的性质,设 ,则 ,代入计算即可.
5.【答案】A
【解析】【解答】解:∵ ,
∴ ,
∵DE=4,
∴EF=10.
故答案为:A.
【分析】根据平行线分线段成比例的性质,列出等式计算即可.
6.【答案】A
【解析】解答:A、x=2,y=3时, ,故A正确;
C、当y=0时, 无意义,故C错误;
故选:A.
分析:根据比例的性质,代数式求值,可得答案.
7.【答案】B
【解析】【解答】解:∵DE∥BC,
∴ = .
∵AE=2,
∴AC=8
故选B
【分析】根据平行线分线段成比例定理可得 ,然后求解即可.
8.【答案】C
【解析】【解答】解:∵,
∴,
∴,
∴
,
∵,
∴,
∴,
故答案为:C.
【分析】根据平行线的性质可得∠ADE=∠B,∠AED=∠C,证明△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方可得S△ADE的值,然后根据S四边形BCED=S△ABC-S△ADE进行计算.
9.【答案】C
【解析】【解答】解:∵四边形ABCD为正方形,边长为10米,
∴AD=CD=BC=10,FD=CD-CF=6,
∵,
∴,
∴,
∴,
即:,解得AE=25,
故答案为:C.
【分析】利用相似三角形的性质测高。
10.【答案】C
【解析】【解答】∵a//b//c,
∴,
∵,DE=3.6,
∴,
∴EF=3.6÷=2.4,
∴DF=DE+EF=3.6+2.4=6,
故答案为:C.
【分析】利用平行线分线段成比例的性质可得,再结合,DE=3.6,求出EF的长,最后利用线段的和差求出DF的长即可.
11.【答案】9﹣3
【解析】【解答】解:∵点D为AC的黄金分割点(AD>CD),
∴AD= AC═ ×6=3 ﹣3,
∴CD=AC﹣AD=6﹣(3 ﹣3)=9﹣3 .
故答案为9﹣3 .
【分析】根据黄金分割的定义得到AD= AC=3 ﹣3,然后利用CD=AC﹣AD进行计算即可.
12.【答案】6
【解析】【解答】解:∵DE是△ABC的中位线,
∴EF∥BC,
∴△ADE∽△ABC,相似比为 ,
∴△ADE的周长是△ABC的周长的一半,
即 ×12=6cm.
故答案为:6.
【分析】根据三角形中位线得出EF∥BC,从而得出△ADE∽△ABC及其相似比 ,从而得出△ADE的周长是△ABC的周长的一半,从而得出答案.
13.【答案】
【解析】【解答】解:在正方形 中,∠BAD=∠D = 90° ,
∴∠BAM+∠FAM= 90°
在Rt 中,
∵由折叠的性质可得
∴AB=BG,∠FBA=∠FBG
∴BF垂直平分AG,
∴AM=MG,∠AMB= 90°
∴∠BAM+∠ABM= 90°
∴∠ABM=∠FAM
∴
∴ ,∴
∴AM= , ∴AG=
∴GE=5-
故答案为:.
【分析】先根据勾股定理得出AE的长,然后根据折叠的性质可得BF垂直平分AG,再根据 ,求出AM 的长,从而得出AG,继而得出GE的长
14.【答案】
【解析】【解答】解:连接AC,AG,
∵在矩形ABCD和矩形AEGH中,
∴∠DAH+∠HAB=90°,∠BAE+∠HAB=90°,HG=AE,
∴∠DAH=∠BAE,
∵AD∶AB=AH∶AE=1∶2,
∴△ADH∽△ABE,
∴DH:BE=AD:AB=1:2,
在Rt△AHG中,HG=2AH,
∴,
∴AH:AG:AE=1::2,
当AH与DA重合时,将矩形AHGE绕着点A旋转至矩形AHGE,
∴△ACG∽△ABE∽△ADH,
∴
∴DH:CG:BE=1::2.
故答案为:1::2
【分析】连接AC,AG,利用矩形的性质和余角的性质可证得HG=AE,∠DAH=∠BAE,利用有两组对应边成比例且夹角相等的两三角形相似,可证得△ADH∽△ABE,利用相似三角形的对应边成比例,可得到DH:BE的比值,利用勾股定理可表示出AG的长,可得到AH:AG:AE的比值;再证明△ACG∽△ABE∽△ADH,利用相似三角形的对应边成比例,可求出DH:CG:BE的坐标.
15.【答案】解:过点B、B'分别作BD⊥x轴于D,B'E⊥x轴于E,
∴∠BDC=∠B'EC=90°.
∵△ABC的位似图形是△A'B'C,
∴点B、C、B'在一条直线上,
∴∠BCD=∠B'CE,
∴△BCD∽△B'CE.
∴,
又∵,
∴,
又∵点B'的横坐标是2,点C的坐标是(﹣1,0),
∴CE=3,
∴.
∴,
∴点B的横坐标为- .
【解析】【分析】过B和B′向x轴引垂线,构造相似比为1:2的相似三角形,那么利用相似比和所给B′的横坐标即可求得点B的横坐标.
16.【答案】证明:∵∠1=∠2,∠3=∠4,
∴△ABD∽△CBE,
∴
∴
∵∠1=∠2,
∴∠1+∠DBC=∠2+∠DBC,
∴∠ABC=∠DBE,
∴△ABC∽△DBE,
【解析】【分析】求出△ABD∽△CBE,得出 ,即 ,再求出∠ABC=∠DBE,即可证△ABC∽△DBE.
17.【答案】解:过C点作AB的平行线,交x轴于D1点,
则△DOC∽△AOB, ,
即 ,解得OD= ,
∴D1(﹣ ,0),根据对称得D2( ,0);
由△COD∽△AOB,得D3(﹣6,0),根据对称得D4(6,0).
【解析】【分析】过C点作AB的平行线,交x轴于D1点,由平行得相似可知D1点符合题意,根据对称得D2点;改变相似三角形的对应关系得D3点,利用对称得D4点,都满足题意.
18.【答案】证明:∵四边形DEFG是正方形
∴,
∴
∴
∴
∴
∵
∴
【解析】【分析】利用相似三角形的判定与性质证明求解即可。
19.【答案】(1)证明: ,且 ,
(2)解:由(1)得: ,
,且 ,
,
又∵ , , ,
,
解得 .
【解析】【分析】(1)图形中隐含对顶角相等,利用有两组对应角相等的两三角形相似可证得结论。
(2)利用有两边对应成比例且夹角相等的两三角形相似,可证得△DCP∽△ABP,利用相似三角形的对应边成比例,建立关于AB的方程,解方程求出AB的值。
20.【答案】(1)证明: 是△ 重心
,
又 ∥ ,
, ,
则
(2)解:(1)中结论成立,理由如下:
如图,过点 作 ∥ 交 的延长线于点 , 、 的延长线相交于点 ,
则 ,
又
而 是 的中点,即
又
结论成立
(3)解:(1)中结论不成立,理由如下:
当 点与 点重合时, 为 中点, ,
点 在 的延长线上时, ,
,则 ,
同理:当点 在 的延长线上时, ,
结论不成立.
【解析】【分析】(1)重心:三条中线的交点,其到顶点的距离是到对边中点距离的两倍。根据已知条件,判定△AEF∽△ABC,对应边成比例,分析即可证明 。
(2)结论仍成立。同(1), 过点 作 ∥ 交 的延长线于点 , 、 的延长线相交于点 ,判定三角形相似,然后对应边成比例。根据重心的性质,等式替换,分析即可证明结论。
(3)当 点与 点重合时, 为 中点, 。 点 在 的延长线上时 ,>1, 则 ,结论不成立。同理E在AB延长线时, 也不符合结论。
21.【答案】(1)解:结论:CF=2DG.理由:∵四边形ABCD是正方形,∴AD=BC=CD=AB,∠ADC=∠C=90°∵DE=AE,
∴AD=CD=2DE,
∵EG⊥DF,∴∠DHG=90°,∴∠CDF+∠DGE=90°,∠DGE+∠DEG=90°,∴∠CDF=∠DEG,
∴△DEG∽△CDF,
∴CF=2DG
(2)解:作点C关于NM的对称点K,连接DK交MN于点P,连接PC,
此时△PDC的周长最短.周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK.
【解析】【分析】(1)根据正方形的性质及中点的定义,可证得AD=CD=2DE,再证明△DEG∽△CDF,得出对应边成比例,就可证得结论。
(2)作点C关于NM的对称点K,连接DK交MN于点P,连接PC,此时△PDC的周长最短.周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK,根据相似三角形的判断和性质,可求出DH、HM的长,再利用勾股定理求出DM、DK的长,然后求出CD与DK之和即可。
22.【答案】(1)解:∵在Rt△ABC中,∠B=90°,BC=4cm,AB=8cm, ∴tanA= = ,
∵D是AB中点,
∴DE是△ABC的中位线,
∴AD=BD=4cm,DE=2cm,
∴Rt△APQ中,AP=3cm,
∴PQ=AP tanA=3× =1.5cm,
∴DN=AN﹣AD=AP+PN﹣AD=3+1.5﹣4=0.5,
∴重合部分的面积应该是y=DN×MN=1.5×0.5=0.75cm2
(2)解:当0<x≤ ,y=0;
当 <x≤4,y= ,
当4<x≤ ,y=x;
当 <x<8,y=16﹣2x;
(3)解:当 <x≤4时,如果y=2,2= ,解得x= 或x= (舍去);
当4<x≤ 时,如果y=2,x=2,也错误,
当 <x<8时,如果y=2,2=16﹣2x,解得x=7,因此当AP=7cm时,y=2cm2.
∴当x=7cm或x= cm时,y=2cm2.
【解析】【分析】(1)先根据AP的长,求出PQ的值,然后看看正方形与矩形是否重合,若重合求出重合部分的线段的长,然后根据矩形的面积计算公式进行求解即可.(2)要分四种情况进行讨论:①当N在D点或D点左侧时,当正方形PQMN的边MN与矩形EDBF的边ED重合时,利用相似三角形的性质可得出x= ,即0<x≤ 时,此时正方形与矩形没有重合,因此y=0;②当N在D点右侧,而P点在D点左侧或与D点重合时,即 <x≤4,此时正方形与矩形重合的面积应该是以DN为长,NM为宽的矩形,DN=PN﹣PD=PN﹣(AD﹣AP)=x﹣(4﹣ x)= x﹣4.而NM=PQ= x,因此重合部分的面积应该是y=( x﹣4)× x= x2﹣2x;③当P在D点右侧,而N点在B点左侧或与B点重合时,即4<x≤ 时,此时正方形重合部分的面积应该是以正方形边长为长,DE为宽的矩形的面积,PN= x,DE=2,因此此时重合部分的面积是y= x×2=x;④当P在B左侧时,而N点在AB延长线上时,即 <x<8时,此时重合部分的面积应该是以DE长为宽,PA长为长的矩形的面积.BP=AB﹣AP=8﹣x,BF=DE=2,因此此时重合部分的面积应该是y=(8﹣x)×2=16﹣2x.(3)将y=2代入(2)的式子中,看看求出的x哪个符合条件即可.
23.【答案】(1)解:如图①中,
∵AM⊥DN,
∴∠AMD=90°,
∵tan∠ADM= = ,
∴可以假设AM=3k,DM=4k,则AD=5k,
∵AD⊥AN,
∴∠DAN=90°=∠AMD,
∵∠ADM=∠ADN,
∴△ADM∽△NDA,
∴AD2=DM AN,
∴(5k)2=4k(4k+3),
解得k= ,
∴AD= ,
∵四边形ABCD是平行四边形,
∴BC=AD= .
(2)证明:如图②中,连接CH,在DM上取一点K,使得DK=BH.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADK=∠BNQ,
∵BH∥DQ,
∴∠CBH=∠BNQ,
∴∠ADK=∠CBH,
∵DK=BH,DA=BC,
∴△ADK≌△CBH(SAS),
∴AK=CH,
∵AM⊥DQ,AN⊥AD,AD∥BC,
∴AN⊥BC,
∴∠AMK=∠CNH=90°,
∵AM=CN,
∴Rt△AMK≌Rt△CNH(HL),
∴MK=NH,
∴DM=DK+MK=BH+HN.
【解析】【分析】(1)如图①中,设AM=3k,DM=4k,则AD=5k,由△ADM∽△NDA,可得AD2=DM AN,由此构建方程即可解决问题.(2)如图②中,连接CH,在DM上取一点K,使得DK=BH.证明△ADK≌△CBH(SAS),推出AK=CH,再证明Rt△AMK≌Rt△CNH(HL),推出MK=HN即可解决问题.
一、单选题
1.如图,矩形ABCD中,点E为AB边中点,连接AC、DE交于点F,若的面积为4,则的面积为( )
A.3 B.4 C.6 D.8
2.一种数学课本的宽与长之比为黄金比,已知它的长是26cm,那么它的宽是( )cm。
A.+26 B.-26 C.+14 D.-13
3.下列命题中的真命题是( )
A.两个直角三角形都相似
B.若一个直角三角形的两条边和另一个直角三角形的两条边成比例,则这两个直角三角形相似
C.两个等腰三角形都相似
D.两个等腰直角三角形都相似
4.已知 ,则 的值为( )
A. B. C. D.
5.如图,l1 l2 l3,直线a,b与l1,l2,l3分别相交于A,B,C和D,E,F.若 ,DE=4,则EF的长为( )
A.10 B. C.12 D.14
6.已知 ,那么下列等式一定成立的是( )
A.x=2,y=3 B. C. D.
7.如图,D,E为△ABC的边AB,AC上的点,DE∥BC,若AD:DB=1:3,AE=2,则AC的长是( )
A.10 B.8 C.6 D.4
8.如图,在中,,,若,则等于( )
A.7 B.4 C.8 D.6
9.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形ABCD,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线BE与边DC相交于点F,如果测得米,那么塔与树的距离AE为( )
A.15米 B.20米 C.25米 D.30米
10. 如图,直线m分别交直线a,b,c于点A,B,C,直线n分别交直线a,b,c于点D,E,F.若,,则DF的长为( )
A.2.4 B.3.6 C.6 D.7.2
二、填空题
11.如图,△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,点D为AC的黄金分割点(AD>CD),AC=6,则CD= .
12.如图,EF为△ABC的中位线,△ABC的周长为12cm,则△AEF的周长为 cm.
13.如图,正方形纸片 的边长为12, 是边 上一点,连接 .折叠该纸片,使点 落在 上的 点,并使折痕经过点 ,得到折痕 ,点 在 上.若 ,则 的长为 .
14.如图,在矩形ABCD和矩形AEGH中,AD∶AB=AH∶AE=1∶2.则DH∶CG∶BE= .
三、解答题
15.如图,△ABC中,A、B两点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,求点B的横坐标.
16.如图,已知D为 内一点,E为 外一点,且 , .求证: .
17.在直角坐标系中,已知点A(﹣2,0),B(0,4),C(0,3),过点C作直线交x轴于点D,使得以D,O,C为顶点的三角形与△AOB相似,求点D的坐标.
18.如图,中有内接正方形DEFG,DE在BC边上,顶点G、F分别在AB、AC边上,,垂足为H,交GF于I.求证:.
四、综合题
19.已知,四边形 的两条对角相交于点 , .
(1)求证: .
(2)若 , ,求 的长.
20.在△ 中,已知 是 边的中点, 是△ 的重心,过 点的直线分别交 、 于点 、 .
(1)如图1,当 ∥ 时,求证: ;
(2)如图2,当 和 不平行,且点 、 分别在线段 、 上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
(3)如图3,当点 在 的延长线上或点 在 的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
21.如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.
22.已知:在Rt△ABC中,∠B=90°,BC=4cm,AB=8cm,D、E、F分别为AB、AC、BC边上的中点.若P为AB边上的一个动点,PQ∥BC,且交AC于点Q,以PQ为一边,在点A的异侧作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.
(1)如图,当AP=3cm时,求y的值;
(2)设AP=xcm,试用含x的代数式表示y(cm2);
(3)当y=2cm2时,试确定点P的位置.
23.已知平行四边形ABCD中,N是边BC上一点,延长DN、AB交于点Q,过A作AM⊥DN于点M,连接AN,则AD⊥AN.
(1)如图①,若tan∠ADM= ,MN=3,求BC的长;
(2)如图②,过点B作BH∥DQ交AN于点H,若AM=CN,求证:DM=BH+NH.
答案解析部分
1.【答案】A
【解析】【解答】解:∵四边形ABCD是矩形,
∴ABCD,AB=CD,
∴△AEF∽△CDF,
∵点E是AB中点,
∴CD=AB=2AE,
∴,
∵的面积为4,
∴△AEF的面积为1,
∴△ADF的面积为2,
∴的面积为3,
故答案为:A.
【分析】先证明△AEF∽△CDF,可得,再结合的面积为4,可得△AEF的面积为1,最后求出的面积为3即可。
2.【答案】D
【解析】【解答】解: ∵书的宽与长之比为黄金比,长为26cm,
∴它的宽=.
故答案为:D.
【分析】 根据黄金分割的定义得到书的宽与长之比为,得出它的宽为,即可得出答案.
3.【答案】D
【解析】【解答】解:A. 两个直角三角形不一定都相似,故A不符合题意;
B. 若一个直角三角形的两条边和另一个直角三角形的两条边成比例,则这两个直角三角形不一定相似,故B不符合题意;
C. 两个等腰三角形不一定都相似,故C不符合题意;
D.两个等腰直角三角形都相似,故D符合题意.
故答案为:D.
【分析】本题考查相似三角形的判定,根据相似三角形的判定方法逐项进行判断,即可求解.
4.【答案】A
【解析】【解答】∵ ,
设 ,则 ,
∴ ,
故答案为:A.
【分析】根据比例的性质,设 ,则 ,代入计算即可.
5.【答案】A
【解析】【解答】解:∵ ,
∴ ,
∵DE=4,
∴EF=10.
故答案为:A.
【分析】根据平行线分线段成比例的性质,列出等式计算即可.
6.【答案】A
【解析】解答:A、x=2,y=3时, ,故A正确;
C、当y=0时, 无意义,故C错误;
故选:A.
分析:根据比例的性质,代数式求值,可得答案.
7.【答案】B
【解析】【解答】解:∵DE∥BC,
∴ = .
∵AE=2,
∴AC=8
故选B
【分析】根据平行线分线段成比例定理可得 ,然后求解即可.
8.【答案】C
【解析】【解答】解:∵,
∴,
∴,
∴
,
∵,
∴,
∴,
故答案为:C.
【分析】根据平行线的性质可得∠ADE=∠B,∠AED=∠C,证明△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方可得S△ADE的值,然后根据S四边形BCED=S△ABC-S△ADE进行计算.
9.【答案】C
【解析】【解答】解:∵四边形ABCD为正方形,边长为10米,
∴AD=CD=BC=10,FD=CD-CF=6,
∵,
∴,
∴,
∴,
即:,解得AE=25,
故答案为:C.
【分析】利用相似三角形的性质测高。
10.【答案】C
【解析】【解答】∵a//b//c,
∴,
∵,DE=3.6,
∴,
∴EF=3.6÷=2.4,
∴DF=DE+EF=3.6+2.4=6,
故答案为:C.
【分析】利用平行线分线段成比例的性质可得,再结合,DE=3.6,求出EF的长,最后利用线段的和差求出DF的长即可.
11.【答案】9﹣3
【解析】【解答】解:∵点D为AC的黄金分割点(AD>CD),
∴AD= AC═ ×6=3 ﹣3,
∴CD=AC﹣AD=6﹣(3 ﹣3)=9﹣3 .
故答案为9﹣3 .
【分析】根据黄金分割的定义得到AD= AC=3 ﹣3,然后利用CD=AC﹣AD进行计算即可.
12.【答案】6
【解析】【解答】解:∵DE是△ABC的中位线,
∴EF∥BC,
∴△ADE∽△ABC,相似比为 ,
∴△ADE的周长是△ABC的周长的一半,
即 ×12=6cm.
故答案为:6.
【分析】根据三角形中位线得出EF∥BC,从而得出△ADE∽△ABC及其相似比 ,从而得出△ADE的周长是△ABC的周长的一半,从而得出答案.
13.【答案】
【解析】【解答】解:在正方形 中,∠BAD=∠D = 90° ,
∴∠BAM+∠FAM= 90°
在Rt 中,
∵由折叠的性质可得
∴AB=BG,∠FBA=∠FBG
∴BF垂直平分AG,
∴AM=MG,∠AMB= 90°
∴∠BAM+∠ABM= 90°
∴∠ABM=∠FAM
∴
∴ ,∴
∴AM= , ∴AG=
∴GE=5-
故答案为:.
【分析】先根据勾股定理得出AE的长,然后根据折叠的性质可得BF垂直平分AG,再根据 ,求出AM 的长,从而得出AG,继而得出GE的长
14.【答案】
【解析】【解答】解:连接AC,AG,
∵在矩形ABCD和矩形AEGH中,
∴∠DAH+∠HAB=90°,∠BAE+∠HAB=90°,HG=AE,
∴∠DAH=∠BAE,
∵AD∶AB=AH∶AE=1∶2,
∴△ADH∽△ABE,
∴DH:BE=AD:AB=1:2,
在Rt△AHG中,HG=2AH,
∴,
∴AH:AG:AE=1::2,
当AH与DA重合时,将矩形AHGE绕着点A旋转至矩形AHGE,
∴△ACG∽△ABE∽△ADH,
∴
∴DH:CG:BE=1::2.
故答案为:1::2
【分析】连接AC,AG,利用矩形的性质和余角的性质可证得HG=AE,∠DAH=∠BAE,利用有两组对应边成比例且夹角相等的两三角形相似,可证得△ADH∽△ABE,利用相似三角形的对应边成比例,可得到DH:BE的比值,利用勾股定理可表示出AG的长,可得到AH:AG:AE的比值;再证明△ACG∽△ABE∽△ADH,利用相似三角形的对应边成比例,可求出DH:CG:BE的坐标.
15.【答案】解:过点B、B'分别作BD⊥x轴于D,B'E⊥x轴于E,
∴∠BDC=∠B'EC=90°.
∵△ABC的位似图形是△A'B'C,
∴点B、C、B'在一条直线上,
∴∠BCD=∠B'CE,
∴△BCD∽△B'CE.
∴,
又∵,
∴,
又∵点B'的横坐标是2,点C的坐标是(﹣1,0),
∴CE=3,
∴.
∴,
∴点B的横坐标为- .
【解析】【分析】过B和B′向x轴引垂线,构造相似比为1:2的相似三角形,那么利用相似比和所给B′的横坐标即可求得点B的横坐标.
16.【答案】证明:∵∠1=∠2,∠3=∠4,
∴△ABD∽△CBE,
∴
∴
∵∠1=∠2,
∴∠1+∠DBC=∠2+∠DBC,
∴∠ABC=∠DBE,
∴△ABC∽△DBE,
【解析】【分析】求出△ABD∽△CBE,得出 ,即 ,再求出∠ABC=∠DBE,即可证△ABC∽△DBE.
17.【答案】解:过C点作AB的平行线,交x轴于D1点,
则△DOC∽△AOB, ,
即 ,解得OD= ,
∴D1(﹣ ,0),根据对称得D2( ,0);
由△COD∽△AOB,得D3(﹣6,0),根据对称得D4(6,0).
【解析】【分析】过C点作AB的平行线,交x轴于D1点,由平行得相似可知D1点符合题意,根据对称得D2点;改变相似三角形的对应关系得D3点,利用对称得D4点,都满足题意.
18.【答案】证明:∵四边形DEFG是正方形
∴,
∴
∴
∴
∴
∵
∴
【解析】【分析】利用相似三角形的判定与性质证明求解即可。
19.【答案】(1)证明: ,且 ,
(2)解:由(1)得: ,
,且 ,
,
又∵ , , ,
,
解得 .
【解析】【分析】(1)图形中隐含对顶角相等,利用有两组对应角相等的两三角形相似可证得结论。
(2)利用有两边对应成比例且夹角相等的两三角形相似,可证得△DCP∽△ABP,利用相似三角形的对应边成比例,建立关于AB的方程,解方程求出AB的值。
20.【答案】(1)证明: 是△ 重心
,
又 ∥ ,
, ,
则
(2)解:(1)中结论成立,理由如下:
如图,过点 作 ∥ 交 的延长线于点 , 、 的延长线相交于点 ,
则 ,
又
而 是 的中点,即
又
结论成立
(3)解:(1)中结论不成立,理由如下:
当 点与 点重合时, 为 中点, ,
点 在 的延长线上时, ,
,则 ,
同理:当点 在 的延长线上时, ,
结论不成立.
【解析】【分析】(1)重心:三条中线的交点,其到顶点的距离是到对边中点距离的两倍。根据已知条件,判定△AEF∽△ABC,对应边成比例,分析即可证明 。
(2)结论仍成立。同(1), 过点 作 ∥ 交 的延长线于点 , 、 的延长线相交于点 ,判定三角形相似,然后对应边成比例。根据重心的性质,等式替换,分析即可证明结论。
(3)当 点与 点重合时, 为 中点, 。 点 在 的延长线上时 ,>1, 则 ,结论不成立。同理E在AB延长线时, 也不符合结论。
21.【答案】(1)解:结论:CF=2DG.理由:∵四边形ABCD是正方形,∴AD=BC=CD=AB,∠ADC=∠C=90°∵DE=AE,
∴AD=CD=2DE,
∵EG⊥DF,∴∠DHG=90°,∴∠CDF+∠DGE=90°,∠DGE+∠DEG=90°,∴∠CDF=∠DEG,
∴△DEG∽△CDF,
∴CF=2DG
(2)解:作点C关于NM的对称点K,连接DK交MN于点P,连接PC,
此时△PDC的周长最短.周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK.
【解析】【分析】(1)根据正方形的性质及中点的定义,可证得AD=CD=2DE,再证明△DEG∽△CDF,得出对应边成比例,就可证得结论。
(2)作点C关于NM的对称点K,连接DK交MN于点P,连接PC,此时△PDC的周长最短.周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK,根据相似三角形的判断和性质,可求出DH、HM的长,再利用勾股定理求出DM、DK的长,然后求出CD与DK之和即可。
22.【答案】(1)解:∵在Rt△ABC中,∠B=90°,BC=4cm,AB=8cm, ∴tanA= = ,
∵D是AB中点,
∴DE是△ABC的中位线,
∴AD=BD=4cm,DE=2cm,
∴Rt△APQ中,AP=3cm,
∴PQ=AP tanA=3× =1.5cm,
∴DN=AN﹣AD=AP+PN﹣AD=3+1.5﹣4=0.5,
∴重合部分的面积应该是y=DN×MN=1.5×0.5=0.75cm2
(2)解:当0<x≤ ,y=0;
当 <x≤4,y= ,
当4<x≤ ,y=x;
当 <x<8,y=16﹣2x;
(3)解:当 <x≤4时,如果y=2,2= ,解得x= 或x= (舍去);
当4<x≤ 时,如果y=2,x=2,也错误,
当 <x<8时,如果y=2,2=16﹣2x,解得x=7,因此当AP=7cm时,y=2cm2.
∴当x=7cm或x= cm时,y=2cm2.
【解析】【分析】(1)先根据AP的长,求出PQ的值,然后看看正方形与矩形是否重合,若重合求出重合部分的线段的长,然后根据矩形的面积计算公式进行求解即可.(2)要分四种情况进行讨论:①当N在D点或D点左侧时,当正方形PQMN的边MN与矩形EDBF的边ED重合时,利用相似三角形的性质可得出x= ,即0<x≤ 时,此时正方形与矩形没有重合,因此y=0;②当N在D点右侧,而P点在D点左侧或与D点重合时,即 <x≤4,此时正方形与矩形重合的面积应该是以DN为长,NM为宽的矩形,DN=PN﹣PD=PN﹣(AD﹣AP)=x﹣(4﹣ x)= x﹣4.而NM=PQ= x,因此重合部分的面积应该是y=( x﹣4)× x= x2﹣2x;③当P在D点右侧,而N点在B点左侧或与B点重合时,即4<x≤ 时,此时正方形重合部分的面积应该是以正方形边长为长,DE为宽的矩形的面积,PN= x,DE=2,因此此时重合部分的面积是y= x×2=x;④当P在B左侧时,而N点在AB延长线上时,即 <x<8时,此时重合部分的面积应该是以DE长为宽,PA长为长的矩形的面积.BP=AB﹣AP=8﹣x,BF=DE=2,因此此时重合部分的面积应该是y=(8﹣x)×2=16﹣2x.(3)将y=2代入(2)的式子中,看看求出的x哪个符合条件即可.
23.【答案】(1)解:如图①中,
∵AM⊥DN,
∴∠AMD=90°,
∵tan∠ADM= = ,
∴可以假设AM=3k,DM=4k,则AD=5k,
∵AD⊥AN,
∴∠DAN=90°=∠AMD,
∵∠ADM=∠ADN,
∴△ADM∽△NDA,
∴AD2=DM AN,
∴(5k)2=4k(4k+3),
解得k= ,
∴AD= ,
∵四边形ABCD是平行四边形,
∴BC=AD= .
(2)证明:如图②中,连接CH,在DM上取一点K,使得DK=BH.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADK=∠BNQ,
∵BH∥DQ,
∴∠CBH=∠BNQ,
∴∠ADK=∠CBH,
∵DK=BH,DA=BC,
∴△ADK≌△CBH(SAS),
∴AK=CH,
∵AM⊥DQ,AN⊥AD,AD∥BC,
∴AN⊥BC,
∴∠AMK=∠CNH=90°,
∵AM=CN,
∴Rt△AMK≌Rt△CNH(HL),
∴MK=NH,
∴DM=DK+MK=BH+HN.
【解析】【分析】(1)如图①中,设AM=3k,DM=4k,则AD=5k,由△ADM∽△NDA,可得AD2=DM AN,由此构建方程即可解决问题.(2)如图②中,连接CH,在DM上取一点K,使得DK=BH.证明△ADK≌△CBH(SAS),推出AK=CH,再证明Rt△AMK≌Rt△CNH(HL),推出MK=HN即可解决问题.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
