北师大版九年级数学高频考点培优讲义(1)(动点最值问题专题)(无答案)
文档属性
| 名称 | 北师大版九年级数学高频考点培优讲义(1)(动点最值问题专题)(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 665.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 00:00:00 | ||
图片预览

文档简介
北师大版九年级数学高频考点培优讲义(1)(动点最值问题专题)
选择题。
1.如图,在△ABC中,AB的垂直平分线DE交BC于点D,垂足为E,M为DE上任意一点,BA=3,AC=4,BC=6,则△AMC周长的最小值为( )
A.7 B.6 C.9 D.10
2.如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )
A.0 B.4 C.6 D.8
3.如图,点D是等边△ABC内一点,AD=3,BD=3,CD=,△ACE是由△ABD绕点A逆时针旋转得到的,则∠ADC的度数是( )
A.40° B.45° C.105° D.55°
4.如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为( )
A.3+2 B.4+3 C.2+2 D.10
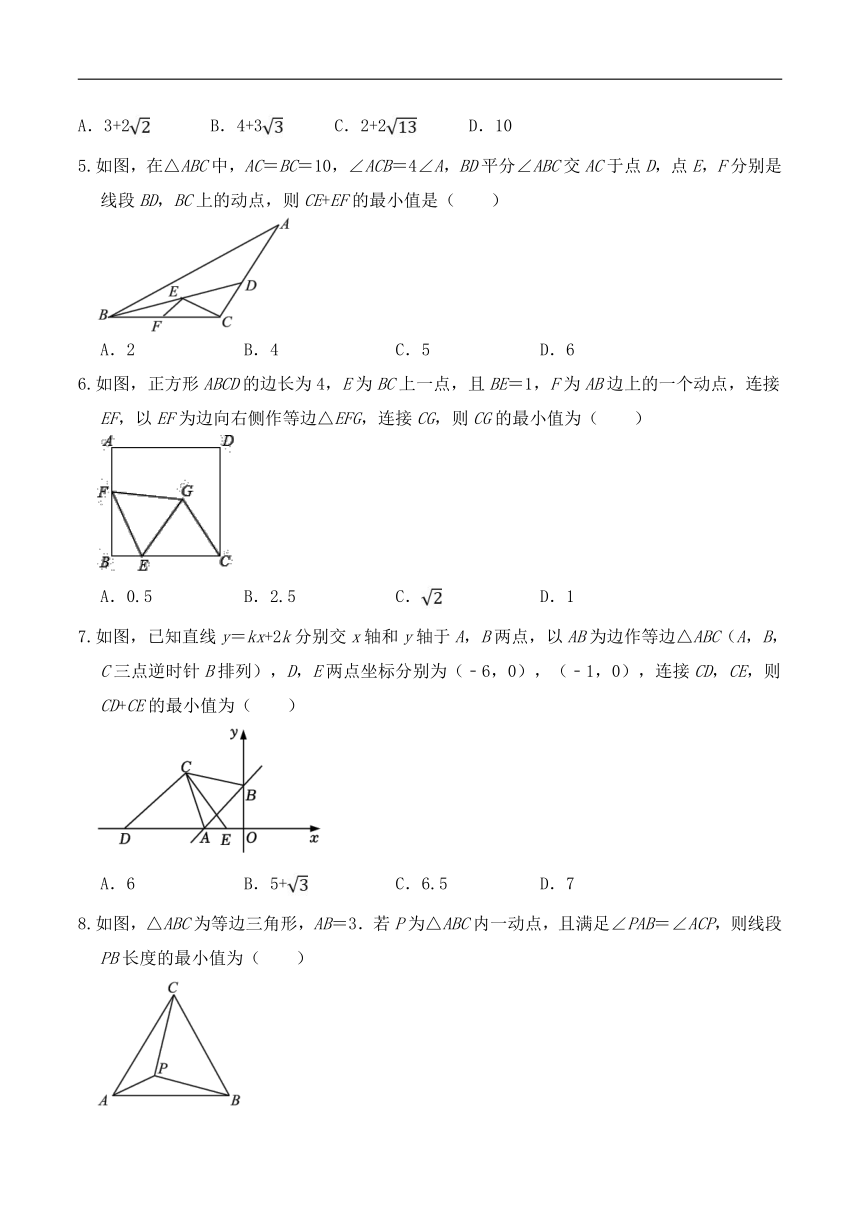
5.如图,在△ABC中,AC=BC=10,∠ACB=4∠A,BD平分∠ABC交AC于点D,点E,F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A.2 B.4 C.5 D.6
6.如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为( )
A.0.5 B.2.5 C. D.1
7.如图,已知直线y=kx+2k分别交x轴和y轴于A,B两点,以AB为边作等边△ABC(A,B,C三点逆时针B排列),D,E两点坐标分别为(﹣6,0),(﹣1,0),连接CD,CE,则CD+CE的最小值为( )
A.6 B.5+ C.6.5 D.7
8.如图,△ABC为等边三角形,AB=3.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为( )
A.1.5 B. C. D.2
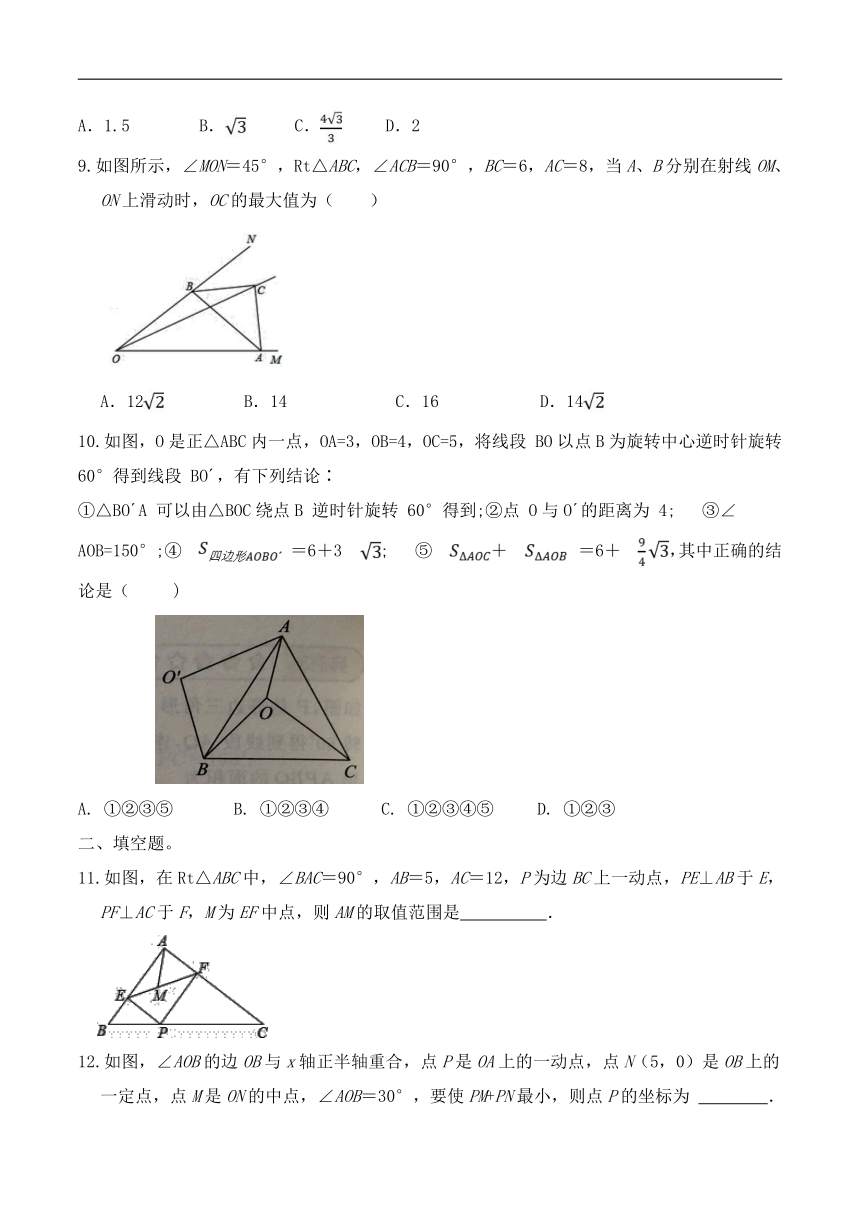
9.如图所示,∠MON=45°,Rt△ABC,∠ACB=90°,BC=6,AC=8,当A、B分别在射线OM、ON上滑动时,OC的最大值为( )
A.12 B.14 C.16 D.14
10.如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段 BO以点B为旋转中心逆时针旋转 60°得到线段 BO ,有下列结论∶
①△BO A 可以由△BOC绕点B 逆时针旋转 60°得到;②点 O与O 的距离为 4; ③∠AOB=150°;④ =6+3; ⑤+ =6+,其中正确的结论是( )
A. ①②③⑤ B. ①②③④ C. ①②③④⑤ D. ①②③
填空题。
11.如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是 .
12.如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(5,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为 .
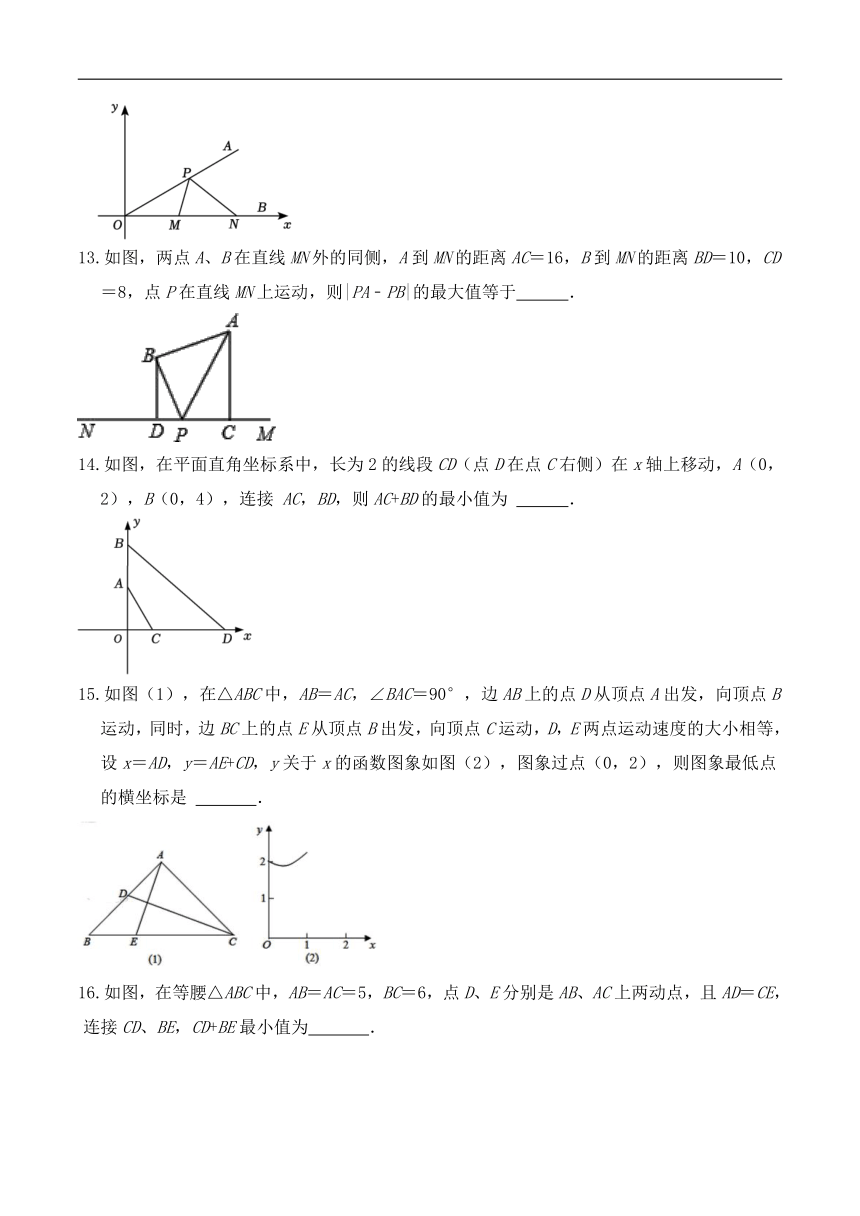
13.如图,两点A、B在直线MN外的同侧,A到MN的距离AC=16,B到MN的距离BD=10,CD=8,点P在直线MN上运动,则|PA﹣PB|的最大值等于 .
14.如图,在平面直角坐标系中,长为2的线段CD(点D在点C右侧)在x轴上移动,A(0,2),B(0,4),连接 AC,BD,则AC+BD的最小值为 .
15.如图(1),在△ABC中,AB=AC,∠BAC=90°,边AB上的点D从顶点A出发,向顶点B运动,同时,边BC上的点E从顶点B出发,向顶点C运动,D,E两点运动速度的大小相等,设x=AD,y=AE+CD,y关于x的函数图象如图(2),图象过点(0,2),则图象最低点的横坐标是 .
16.如图,在等腰△ABC中,AB=AC=5,BC=6,点D、E分别是AB、AC上两动点,且AD=CE,连接CD、BE,CD+BE最小值为 .
17.如图,在Rt△ABC中,∠C=90°,AC=BC=8,点P为AB的中点,E为BC上一动点,过C、E、P三点⊙O交AC于F点,连接EF,则EF的最小值为 .
18.在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于点A(﹣3,0)、B(1,0),点M(﹣1,4)为抛物线的顶点,AM中点D坐标为(﹣2,2);如图,Q点为y轴上一动点,直接写出DQ+OQ的最小值为 .
解答题。
19.如图,四边形ABCD是菱形,AB=4,且∠ABC=60°,M为对角线BD(不含B点)上任意一点.
(1)求AM+BM+CM的最小值;
(2)求AM+BM的最小值.
20.(1)如图1,OC平分∠AOB,点D是射线OA边上一点,点P、Q分别在射线OC、OB上运动,已知OD=10,∠AOC=30°,则DP+PQ的最小值是 ;
(2)如图2,在菱形ABCD中,AB=8,∠DAB=60°,点E是AB边上的动点,点F是对角线AC上的动点,求EF+BF的最小值;
(3)如图3,在矩形ABCD中,AB=8,AD=4,点M是AB上一动点,点N是对角线AC上一动点,请直接写出MN+BN的最小值.
21.如图1,在平面直角坐标系中将y=2x+1向下平移3个单位长度得到直线l1,直线l1与x轴交于点C;直线l2:y=x+2与x轴、y轴交于A、B两点,且与直线l1交于点D.
(1)填空:点A的坐标为 ,点B的坐标为 ;
(2)直线l1的表达式为 ;
(3)在直线l1上是否存在点E,使S△AOE=2S△ABO?若存在,则求出点E的坐标;若不存在,请说明理由.
(4)如图2,点P为线段AD上一点(不含端点),连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
22.阅读下面材料:
小明遇到这样一个问题:如图1,在等边三角形ABC内有一点P,且PA=3,PB=4,PC=5,求∠APB度数.
小明发现,利用旋转和全等的知识构造△AP′C,连接PP′,得到两个特殊的三角形,从而将问题解决(如图2).
请回答:图1中∠APB的度数等于 ,图2中∠PP′C的度数等于 .
参考小明思考问题的方法,解决问题:
如图3,在平面直角坐标系xOy中,点A坐标为(,1),连接AO.如果点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x之间的函数表达式.
23.如图所示,抛物线y=x2﹣2x﹣3与x轴相交于A、B两点,与y轴相交于点C点M为抛物线的顶点.
(1)求点C及顶点M的坐标;
(2)在抛物线的对称轴上找一点P,使得△ACP的周长最小,请求出点P的坐标;
(3)若点N是第四象限内抛物线上的一个动点,连接BN、CN,求△BCN面积的最大值及此时点N的坐标.
24. 如图,抛物线y=﹣x2+bx+c与直线AB交于A(﹣4,﹣4),B(0,4)两点,直线AC:y=﹣x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=﹣x2+bx+c的表达式;
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求AM+CM它的最小值.
选择题。
1.如图,在△ABC中,AB的垂直平分线DE交BC于点D,垂足为E,M为DE上任意一点,BA=3,AC=4,BC=6,则△AMC周长的最小值为( )
A.7 B.6 C.9 D.10
2.如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )
A.0 B.4 C.6 D.8
3.如图,点D是等边△ABC内一点,AD=3,BD=3,CD=,△ACE是由△ABD绕点A逆时针旋转得到的,则∠ADC的度数是( )
A.40° B.45° C.105° D.55°
4.如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为( )
A.3+2 B.4+3 C.2+2 D.10
5.如图,在△ABC中,AC=BC=10,∠ACB=4∠A,BD平分∠ABC交AC于点D,点E,F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A.2 B.4 C.5 D.6
6.如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为( )
A.0.5 B.2.5 C. D.1
7.如图,已知直线y=kx+2k分别交x轴和y轴于A,B两点,以AB为边作等边△ABC(A,B,C三点逆时针B排列),D,E两点坐标分别为(﹣6,0),(﹣1,0),连接CD,CE,则CD+CE的最小值为( )
A.6 B.5+ C.6.5 D.7
8.如图,△ABC为等边三角形,AB=3.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为( )
A.1.5 B. C. D.2
9.如图所示,∠MON=45°,Rt△ABC,∠ACB=90°,BC=6,AC=8,当A、B分别在射线OM、ON上滑动时,OC的最大值为( )
A.12 B.14 C.16 D.14
10.如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段 BO以点B为旋转中心逆时针旋转 60°得到线段 BO ,有下列结论∶
①△BO A 可以由△BOC绕点B 逆时针旋转 60°得到;②点 O与O 的距离为 4; ③∠AOB=150°;④ =6+3; ⑤+ =6+,其中正确的结论是( )
A. ①②③⑤ B. ①②③④ C. ①②③④⑤ D. ①②③
填空题。
11.如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是 .
12.如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(5,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为 .
13.如图,两点A、B在直线MN外的同侧,A到MN的距离AC=16,B到MN的距离BD=10,CD=8,点P在直线MN上运动,则|PA﹣PB|的最大值等于 .
14.如图,在平面直角坐标系中,长为2的线段CD(点D在点C右侧)在x轴上移动,A(0,2),B(0,4),连接 AC,BD,则AC+BD的最小值为 .
15.如图(1),在△ABC中,AB=AC,∠BAC=90°,边AB上的点D从顶点A出发,向顶点B运动,同时,边BC上的点E从顶点B出发,向顶点C运动,D,E两点运动速度的大小相等,设x=AD,y=AE+CD,y关于x的函数图象如图(2),图象过点(0,2),则图象最低点的横坐标是 .
16.如图,在等腰△ABC中,AB=AC=5,BC=6,点D、E分别是AB、AC上两动点,且AD=CE,连接CD、BE,CD+BE最小值为 .
17.如图,在Rt△ABC中,∠C=90°,AC=BC=8,点P为AB的中点,E为BC上一动点,过C、E、P三点⊙O交AC于F点,连接EF,则EF的最小值为 .
18.在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于点A(﹣3,0)、B(1,0),点M(﹣1,4)为抛物线的顶点,AM中点D坐标为(﹣2,2);如图,Q点为y轴上一动点,直接写出DQ+OQ的最小值为 .
解答题。
19.如图,四边形ABCD是菱形,AB=4,且∠ABC=60°,M为对角线BD(不含B点)上任意一点.
(1)求AM+BM+CM的最小值;
(2)求AM+BM的最小值.
20.(1)如图1,OC平分∠AOB,点D是射线OA边上一点,点P、Q分别在射线OC、OB上运动,已知OD=10,∠AOC=30°,则DP+PQ的最小值是 ;
(2)如图2,在菱形ABCD中,AB=8,∠DAB=60°,点E是AB边上的动点,点F是对角线AC上的动点,求EF+BF的最小值;
(3)如图3,在矩形ABCD中,AB=8,AD=4,点M是AB上一动点,点N是对角线AC上一动点,请直接写出MN+BN的最小值.
21.如图1,在平面直角坐标系中将y=2x+1向下平移3个单位长度得到直线l1,直线l1与x轴交于点C;直线l2:y=x+2与x轴、y轴交于A、B两点,且与直线l1交于点D.
(1)填空:点A的坐标为 ,点B的坐标为 ;
(2)直线l1的表达式为 ;
(3)在直线l1上是否存在点E,使S△AOE=2S△ABO?若存在,则求出点E的坐标;若不存在,请说明理由.
(4)如图2,点P为线段AD上一点(不含端点),连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
22.阅读下面材料:
小明遇到这样一个问题:如图1,在等边三角形ABC内有一点P,且PA=3,PB=4,PC=5,求∠APB度数.
小明发现,利用旋转和全等的知识构造△AP′C,连接PP′,得到两个特殊的三角形,从而将问题解决(如图2).
请回答:图1中∠APB的度数等于 ,图2中∠PP′C的度数等于 .
参考小明思考问题的方法,解决问题:
如图3,在平面直角坐标系xOy中,点A坐标为(,1),连接AO.如果点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x之间的函数表达式.
23.如图所示,抛物线y=x2﹣2x﹣3与x轴相交于A、B两点,与y轴相交于点C点M为抛物线的顶点.
(1)求点C及顶点M的坐标;
(2)在抛物线的对称轴上找一点P,使得△ACP的周长最小,请求出点P的坐标;
(3)若点N是第四象限内抛物线上的一个动点,连接BN、CN,求△BCN面积的最大值及此时点N的坐标.
24. 如图,抛物线y=﹣x2+bx+c与直线AB交于A(﹣4,﹣4),B(0,4)两点,直线AC:y=﹣x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=﹣x2+bx+c的表达式;
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求AM+CM它的最小值.
同课章节目录
