苏科版七年级数学下册第七章平面图形的认识二:平行线中的常见模型(含答案)
文档属性
| 名称 | 苏科版七年级数学下册第七章平面图形的认识二:平行线中的常见模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 672.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 16:49:42 | ||
图片预览


文档简介
七年级下册
平面图形的认识(二):
专题:
平行线中的常见四大模型
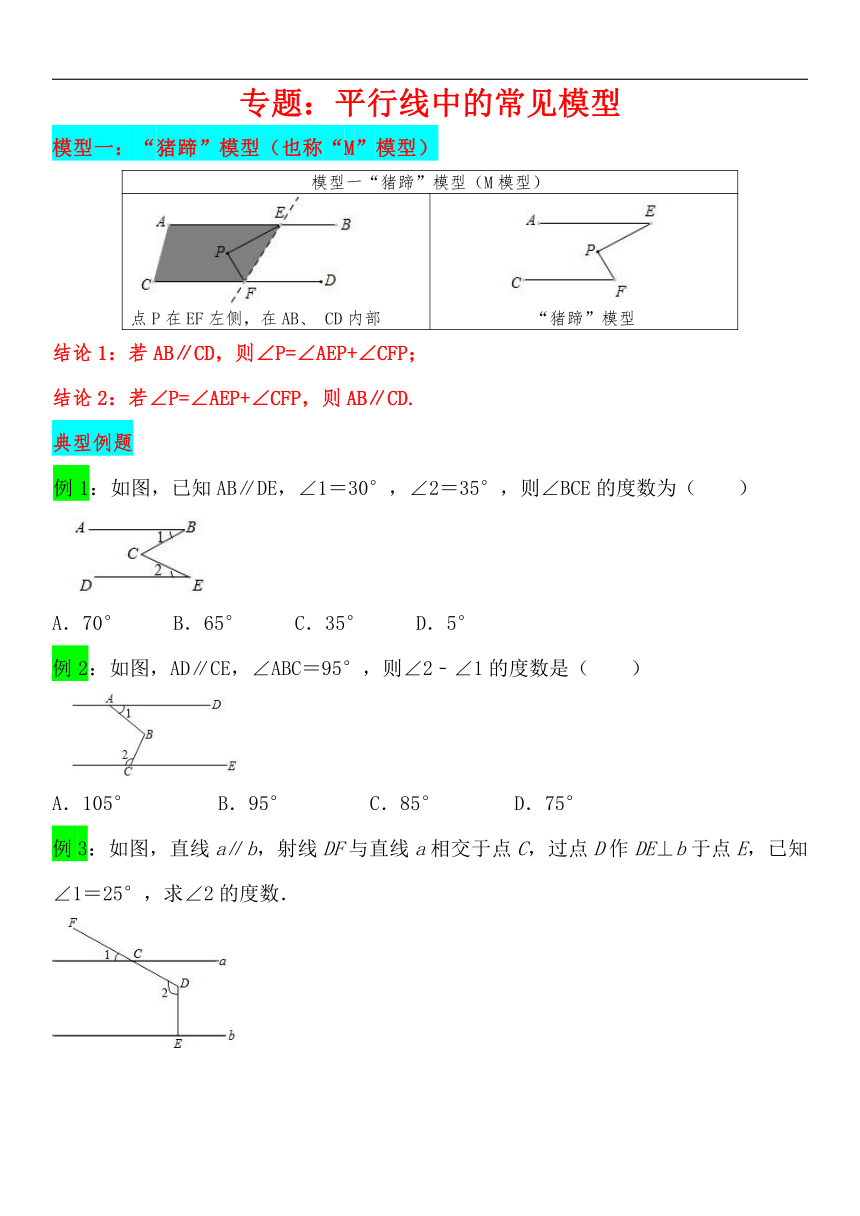
专题:平行线中的常见模型
模型一:“猪蹄”模型(也称“M”模型)
模型一“猪蹄”模型(M模型)
点P在EF左侧,在AB、 CD内部 “猪蹄”模型
结论1:若AB∥CD,则∠P=∠AEP+∠CFP;
结论2:若∠P=∠AEP+∠CFP,则AB∥CD.
典型例题
例1:如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为( )
A.70° B.65° C.35° D.5°
例2:如图,AD∥CE,∠ABC=95°,则∠2﹣∠1的度数是( )
A.105° B.95° C.85° D.75°
例3:如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,求∠2的度数.
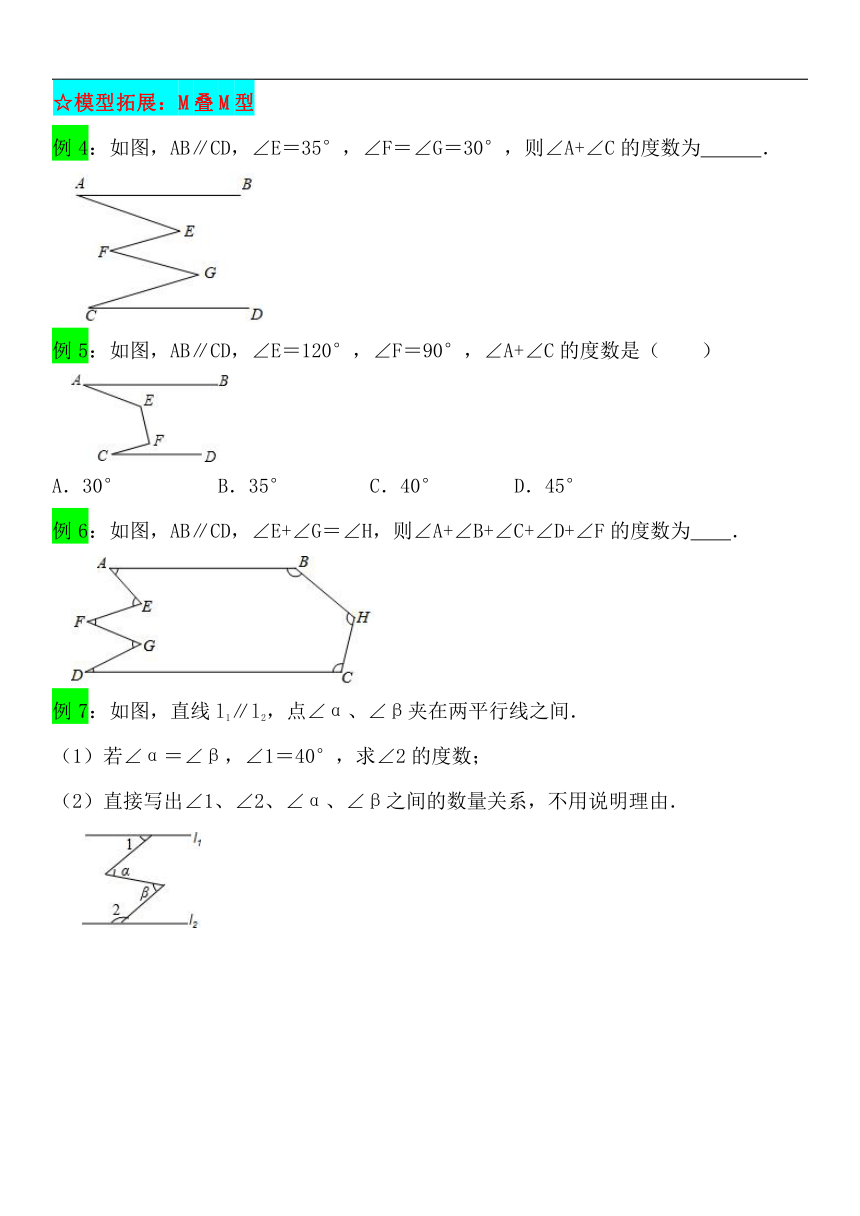
☆模型拓展:M叠M型
例4:如图,AB∥CD,∠E=35°,∠F=∠G=30°,则∠A+∠C的度数为 .
例5:如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )
A.30° B.35° C.40° D.45°
例6:如图,AB∥CD,∠E+∠G=∠H,则∠A+∠B+∠C+∠D+∠F的度数为 .
例7:如图,直线l1∥l2,点∠α、∠β夹在两平行线之间.
(1)若∠α=∠β,∠1=40°,求∠2的度数;
(2)直接写出∠1、∠2、∠α、∠β之间的数量关系,不用说明理由.
☆模型拓展:M套M型
例8:(1)如图1,已知AB∥CD,若∠EAF=∠EAB,∠ECF=∠ECD,
求证:∠AFC=∠AEC;
(2)如图2,若AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD,求证:∠AFC=∠AEC;
(3)若AB∥CD,∠EAF=∠EAB,∠ECF∠ECD,则∠AFC与∠AEC的数量关系是
(用含有n的代数式表示,不证明).
例9:如图①,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第1次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第2次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第3次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE1C=∠BEC;
(3)从图①开始进行上述的n次操作,若∠BEnC=α°,求∠BEC的大小(直接写出结论).
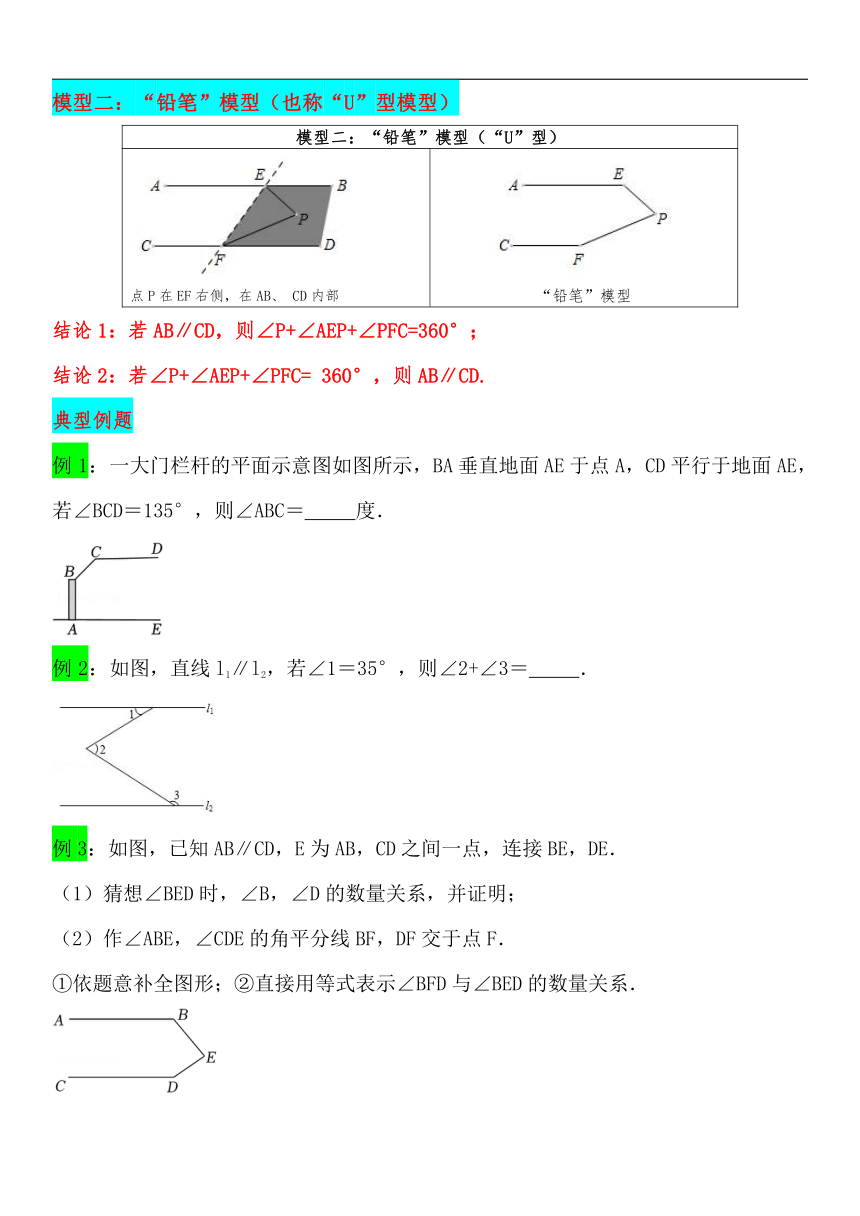
模型二:“铅笔”模型(也称“U”型模型)
模型二:“铅笔”模型(“U”型)
点P在EF右侧,在AB、 CD内部 “铅笔”模型
结论1:若AB∥CD,则∠P+∠AEP+∠PFC=360°;
结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD.
典型例题
例1:一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=135°,则∠ABC= 度.
例2:如图,直线l1∥l2,若∠1=35°,则∠2+∠3= .
例3:如图,已知AB∥CD,E为AB,CD之间一点,连接BE,DE.
(1)猜想∠BED时,∠B,∠D的数量关系,并证明;
(2)作∠ABE,∠CDE的角平分线BF,DF交于点F.
①依题意补全图形;②直接用等式表示∠BFD与∠BED的数量关系.
例4:如图,已知AB∥CD,∠ABE与∠CDE的平分线相交于点F.
(1)如图1,若∠E=70°,求∠BFD的度数;
(2)如图2,若∠ABM=∠ABF,∠CDM=∠CDF,写出∠M和∠E之间的数量关系,并证明你的结论.
例5:实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射的光线为n.
(1)当m∥n时,若∠1=50°,则∠2= ,∠3= ;
(2)当m∥n时,若∠1=x°(0<x<90),则∠3= ;
(3)根据(1)(2)结果,反过来猜想:当两平面镜a,b的夹角∠3为多少度时,m∥n.请说明理由(可以在图中添加适当的角度标记进行说明)
例6:如图,AB∥CD,点E为两直线之间的一点.
(1)如图1,若∠BAE=35°,∠DCE=20°,则∠AEC= ;
(2)如图2,试说明,∠BAE+∠AEC+∠ECD=360°;
(3)①如图3,若∠BAE的平分线与∠DCE的平分线相交于点F,判断∠AEC与∠AFC的数量关系,并说明理由;
②如图4,若设∠E=m,∠BAF=∠FAE,∠DCF=∠FCE,请直接用含m、n的代数式表示∠F的度数.
模型三:“抬头”模型(也称“靴子”或称“臭脚”模型)
模型三“抬头”模型(“靴子”模型)
点P在EF右侧,在AB、 CD外部 “靴子”模型
结论1:若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;
结论2:若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD.
典型例题
例1:如图,AB//CD,∠P=40°,∠D=100°,则∠ABP的度数是 .
例2:已知,AB∥CD.
(1)如图1,求证:∠A-∠C=∠E;
(2)如图2,EF平分∠AEC,CF平分∠ECD,∠F=105°,求∠A的度数.
例3:已知直线∥,点A,B在直线上(B在A左侧),点C在直线b上,E点在直线b下方,连接 AE 交直线b于点D.
(1)如图1,若∠BAD=110°,∠DCE=45°,求∠DEC的度数;
(2)如图2,∠BAD 的邻补角的角平分线与∠DEC 的角平分线所在的直线交于点M,试探究∠AME与∠ECD之间的数量关系,并说明理由.
例4:已知AB∥CD.
(1)如图1,求证:∠EAB=∠C+∠E;
(2)如图2,点F在∠AEC内且在AB、CD之间,EF平分∠AEC,CF平分∠ECD,请猜想∠F与∠EAB的数量关系并证明;
(3)如图3,点M在AB上,点N在CD上,点E是AB上方一点,点G在AB、CD之间,连接EM、EN,GM的延长线MF平分∠AME,NE平分∠CNG,若2∠MEN+∠MGN=105°,求∠AME的度数.:
模型四:“骨折”模型(也称“X射线”模型)
模型四“骨折”模型
点P在EF左侧,在AB、 CD外部 “骨折”模型
结论1:若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;
结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.
例1:如图,AB∥CD,∠E=40°,∠A=110°,则∠C的度数为 .
例2:如图,AB∥CD,∠ABE=125°,∠C=30°,则∠α=( )
A.70° B.75° C.80° D.85°
例3:已知:如图,AB∥CD.
(1)若∠1=∠2,试判断∠E与∠F的大小关系,并说明你的理由.
(2)猜想∠1、∠2、∠E、∠F之间存在怎样的数量关系?并说明理由.
例4:(1)(问题)如图1,若AB∥CD,∠AEP=40°,∠PFD=130°.求∠EPF的度数;
(2)(问题迁移)如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;
(3)(联想拓展)如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.
例5:已知AB∥MN.
(1)如图1,求证:∠N+∠E=∠B;
(2)若F为直线MN、AB之间的一点,∠E=∠EFB,BG平分∠ABF交MN于点G,EF交MN于点C.
①如图2,若∠N=57°,且BG∥EN,求∠E的度数;
②如图3,若点K在射线BG上,且满足∠KNM=∠ENM,若∠NKB=∠EFB,∠E=∠FBD,直接写出∠E的度数.
参考答案
专题四:平行线中的常见模型
模型一:“猪蹄”模型(也称“M”模型)
模型一“猪蹄”模型(M模型)
点P在EF左侧,在AB、 CD内部 “猪蹄”模型
结论1:若AB∥CD,则∠P=∠AEP+∠CFP;
结论2:若∠P=∠AEP+∠CFP,则AB∥CD.
典型例题
例1:如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为(B)
A.70° B.65° C.35° D.5°
解析:作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴AB∥DE∥CF,
∴∠1=∠BCF,∠FCE=∠2,
∵∠1=30°,∠2=35°,
∴∠BCF=30°,∠FCE=35°,
∴∠BCE=65°,故选:B.
例2:如图,AD∥CE,∠ABC=95°,则∠2﹣∠1的度数是(C)
A.105° B.95° C.85° D.75°
解析:如图,作BF∥AD,
∵AD∥CE,
∴AD∥BF∥EC,
∴∠1=∠3,∠4+∠2=180°,∠3+∠4=95°,
∴∠1+∠4=95°,∠2+∠4=180°,
∴∠2﹣∠1=85°.故选:C.
例3:如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,求∠2的度数.
解析:过点D作DG∥b,
∵a∥b,且DE⊥b,
∴DG∥a,
∴∠1=∠CDG=25°,∠GDE=∠3=90°
∴∠2=∠CDG+∠GDE=25°+90°=115°.
☆模型拓展:M叠M型
例4:如图,AB∥CD,∠E=35°,∠F=∠G=30°,则∠A+∠C的度数为35°.
解析:如图所示,延长AE,CG,交于点H,过H作HP∥AB,
∵AB∥CD,
∴PH∥CD,
∴∠A=∠AHP,∠C=∠CHP,
∴∠A+∠C=∠AHC,
∵∠F=∠CGF=30°,
∴EF∥CH,
∴∠AHC=∠AEF=35°,
∴∠A+∠C=35°,
故答案为:35°.
例5:如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )
A.30° B.35° C.40° D.45°
解析:分别过E,F作GE∥AB,FH∥AB,
∵AB∥CD,
∴AB∥GE∥FH∥CD,
∴∠1=∠A,∠2=∠C,∠GEF+∠HFE=180°,
∵∠E=120°,∠F=90°,
∴∠1+∠GEF+∠HFE+∠2=210°,
∴∠1+∠2=210°﹣180°=30°,
即∠A+∠C=30°,故选:A.
例6:如图,AB∥CD,∠E+∠G=∠H,则∠A+∠B+∠C+∠D+∠F的度数为360°.
解析:如图所示,延长AE,DG交于点Q,
由题可得,∠A+∠D=∠Q,∠B+∠H+∠C=360°,
又∵∠Q=∠AEF+∠DGF﹣∠F,
∴∠A+∠D=∠AEF+∠DGF﹣∠F,
即∠F=∠AEF+∠DGF﹣(∠A+∠D),
又∵∠AEF+∠DGF=∠H,
∴∠A+∠B+∠C+∠D+∠F=∠A+∠B+∠C+∠D+∠AEF+∠DGF﹣(∠A+∠D)
=∠B+∠C+∠H
=360°,故答案为:360°.
例7:如图,直线l1∥l2,点∠α、∠β夹在两平行线之间.
(1)若∠α=∠β,∠1=40°,求∠2的度数;
(2)直接写出∠1、∠2、∠α、∠β之间的数量关系,不用说明理由.
解析:(1)如图,延长AE交直线l2于点E,
∵l1∥l2,
∴∠3=∠1=40°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°﹣∠3=180°﹣40°=140°.
(2)∠1+∠2+∠β﹣○α=180°.
理由:∵l1∥l2,
∴∠3=∠1.
∵∠BED=180°﹣∠α,
∴∠3+∠2+∠β+180°﹣α=360°,即∠1+∠2+∠β﹣∠α=180°.
☆模型拓展:M套M型
例8:(1)如图1,已知AB∥CD,若∠EAF=∠EAB,∠ECF=∠ECD,
求证:∠AFC=∠AEC;
(2)如图2,若AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD,求证:∠AFC=∠AEC;
(3)若AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD,则∠AFC与∠AEC的数量关系是
(用含有n的代数式表示,不证明).
解:(1)如图1,连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=2x°,∠ECD=2y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+2x°+∠ACE+2y°=180°,
∴∠CAE+∠ACE=180°﹣(2x°+2y°),∠FAC+∠FCA=180°﹣(x°+y°),
∴∠AEC=180°﹣(∠CAE+∠ACE)
=180°﹣[180°﹣(2x°+2y°)]
=2x°+2y°,
=2(x°+y°),
∠AFC=180°﹣(∠FAC+∠FCA)
=180°﹣[180°﹣(x°+y°)]
=x°+y°,
∴∠AFC=∠AEC;
(2)如图2,连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=3x°,∠ECD=3y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+3x°+∠ACE+3y°=180°,
∴∠CAE+∠ACE=180°﹣(3x°+3y°),∠FAC+∠FCA=180°﹣(2x°+2y°),
∴∠AEC=180°﹣(∠CAE+∠ACE)
=180°﹣[180°﹣(3x°+3y°)]
=3x°+3y°
=3(x°+y°),
∠AFC=180°﹣(∠FAC+∠FCA)
=180°﹣[180°﹣(2x°+2y°)]
=2x°+2y°
=2(x°+y°),
∴∠AFC=∠AEC;
(3)若∠AFC=∠EAB,∠ECF=∠ECD,则∠AFC与∠AEC的数量关系是:∠AFC=∠AEC.
故答案为:∠AFC=∠AEC.
例9:如图①,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第1次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第2次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第3次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE1C=∠BEC;
(3)从图①开始进行上述的n次操作,若∠BEnC=α°,求∠BEC的大小(直接写出结论).
【解答】解:(1)如图①,过E作EF∥AB.
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2.
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
(2)如图2.∵∠ABE和∠DCE的平分线交点为E1,
∴由(1)可得,∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BEC;
(3)如图2.∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC;…
以此类推,∠En=∠BEC,
∴当∠En=α度时,∠BEC=2nα°
模型二:“铅笔”模型(也称“U”型模型)
模型二:“铅笔”模型(“U”型)
点P在EF右侧,在AB、 CD内部 “铅笔”模型
结论1:若AB∥CD,则∠P+∠AEP+∠PFC=360°;
结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD.
典型例题
例1:一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=135°,则∠ABC=135度.
【解析】解:如图,过点B作BF∥CD,
∵CD∥AE,
∴CD∥BF∥AE,
∴∠1+∠BCD=180°,∠2+∠BAE=180°,
∵∠BCD=135°,∠BAE=90°,
∴∠1=45°,∠2=90°,
∴∠ABC=∠1+∠2=135°.
故答案为:135.
例2:如图,直线l1∥l2,若∠1=35°,则∠2+∠3=215°.
【解析】解:过点E作EF∥11,
∵11∥12,EF∥11,
∴EF∥11∥12,
∴∠1=∠AEF=35°,∠FEC+∠3=180°,
∴∠2+∠3=∠AEF+∠FEC+∠3=35°+180°=215°.
故答案为:215°.
例3:如图,已知AB∥CD,E为AB,CD之间一点,连接BE,DE.
(1)猜想∠BED时,∠B,∠D的数量关系,并证明;
(2)作∠ABE,∠CDE的角平分线BF,DF交于点F.
①依题意补全图形;②直接用等式表示∠BFD与∠BED的数量关系.
【解析】(1)∠B+∠BED+∠D=360°.
证明:过点E作EG∥AB.
∴∠B+∠BEG=180°.
∵AB∥CD,EG∥AB,
∴EG∥CD,
∴∠DEG+∠D=180°,
∴∠B+∠BEG+∠DEG+∠D=180°+180°.
即∠B+∠BED+∠D=360°;
(2)解:①如图所示:
②由(1)得∠ABC+∠BED+∠CDE=360°,
∵∠ABE,∠CDE的角平分线BF,DF交于点F,
∴∠ABC=2∠FBE,∠CDE=2∠FDE,
∴2∠FBE+∠BED+2∠CDE=360°,即∠FBE+∠BED+∠CDE=180°,
∵∠BFD+∠FBE+∠BED+∠CDE=360°,
∴∠BFD=180°-∠BED
例4:如图,已知AB∥CD,∠ABE与∠CDE的平分线相交于点F.
(1)如图1,若∠E=70°,求∠BFD的度数;
(2)如图2,若∠ABM=∠ABF,∠CDM=∠CDF,写出∠M和∠E之间的数量关系,并证明你的结论.
【解析】解:(1)如图1,过点E作EN∥AB,
∵EN∥AB,
∴∠ABE+∠BEN=180°,
∵AB∥CD,AB∥NE,
∴NE∥CD,
∴∠CDE+∠NED=180°,
∴∠ABE+∠E+∠CDE=360°,
∵∠E=70°,
∴∠ABE+∠CDE=290°,
∵∠ABE与∠CDE的平分线相交于点F,
∴∠ABF+∠CDF=(∠ABE+∠CDE)=145°,
过点F作FG∥AB,
∵FG∥AB,
∴∠ABF=∠BFG,
∵AB∥CD,FG∥AB,
∴FG∥CD,
∴∠CDF=∠GFD,
∴∠BFD=∠ABF+∠CDF=145°;
(2)结论:∠E+6∠M=360°,
证明:∵设∠ABM=x,∠CDM=y,则∠FBM=2x,∠EBF=3x,∠FDM=2y,∠EDF=3y,
由(1)得:∠ABE+∠E+∠CDE=360°,
∴6x+6y+∠E=360°,
∵∠M+∠EBM+∠E+∠EDM=360°,
∴6x+6y+∠E=∠M+5x+5y+∠E,
∴∠M=x+y,
∴∠E+6∠M=360°.
例5:实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射的光线为n.
(1)当m∥n时,若∠1=50°,则∠2=100°,∠3= 90°;
(2)当m∥n时,若∠1=x°(0<x<90),则∠3= 90°;
(3)根据(1)(2)结果,反过来猜想:当两平面镜a,b的夹角∠3为多少度时,m∥n.请说明理由(可以在图中添加适当的角度标记进行说明)
【解析】解:(1)∵m∥n,
∴∠4+∠2=180°,
∵∠5=∠1=50°,
∴∠4=80°,
∴∠2=100°,
∴∠6=∠7=40°,
∴∠3=180°﹣∠5﹣∠6=90°,
故答案为:100°;90°;
(2)∵m∥n,
∴∠4+∠2=180°,
∵∠5=∠1=x°,
∴∠4=180°﹣2x°,
∴∠2=2x°,
∴∠6=∠7=90°﹣x°,
∴∠3=180°﹣∠5﹣∠6=180°﹣x°﹣90°+x°=90°,
故答案为:90°;
(3)根据(1)、(2)猜想:当两平面镜a、b的夹角∠3是90°时,总有m∥n,
证明:∵∠3=90°,
∴∠5+∠6=90°,
∴∠1+∠7=90°,
∴∠1+∠5+∠6+∠7=180°,
又∵∠1+∠4+∠5+∠2+∠6+∠7=360°,
∴∠4+∠2=180°,
∴m∥n.
例6:如图,AB∥CD,点E为两直线之间的一点.
(1)如图1,若∠BAE=35°,∠DCE=20°,则∠AEC=55°;
(2)如图2,试说明,∠BAE+∠AEC+∠ECD=360°;
(3)①如图3,若∠BAE的平分线与∠DCE的平分线相交于点F,判断∠AEC与∠AFC的数量关系,并说明理由;
②如图4,若设∠E=m,∠BAF=∠FAE,∠DCF=∠FCE,请直接用含m、n的代数式表示∠F的度数.
【解析】解:如图所示,过点E作EF∥AB,
∵AB∥CD∴AB∥CD∥EF,
∴∠BAE=∠1,∠ECD=∠2,
∴∠AEC=∠1+∠2=∠BAE+∠ECD=35°+20°=55°,
故答案为55°.
(2)如图所示,过点E作EG∥AB,
∵AB∥CD∴AB∥CD∥EG,
∴∠A+∠1=180°,∠C+∠2=180°,
∴∠A+∠1+∠2+∠C=360°,
即∠BAE+∠AEC+∠ECD=360°.
(3)①2∠AFC+∠AEC=360°,理由如下:
由(1)可得,∠AFC=∠BAF+∠DCF,
∵AF平分∠BAE,CF平分∠DCE,
∴∠BAE=2∠BAF,∠DCE=2∠DCF,
∴∠BAE+∠DCE=2∠AFC,
由(2)可知,∠BAE+∠AEC+∠DCE=360°,
∴2∠AFC+∠AEC=360°.
②由①知∠F+∠FAE+∠E+∠FCE=360°,
∵∠BAF=∠FAE,∠DCF=∠FCE,∠BAF+∠DCF=∠F,
∴∠F=(∠FAE+∠FCE),
∴∠FAE+∠FCE=n∠F,
∴∠F+∠E+n∠F=360°,
∴(n+1)∠F=360°﹣∠E=360°﹣m,
∴∠F=.
模型三:“抬头”模型(也称“靴子”或称“臭脚”模型)
模型三“抬头”模型(“靴子”模型)
点P在EF右侧,在AB、 CD外部 “靴子”模型
结论1:若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;
结论2:若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD.
典型例题
例1:如图,AB//CD,∠P=40°,∠D=100°,则∠ABP的度数是140°.
【解析】过点P作PM∥AB,
∵AB∥CD,
∴PM∥AB∥CD,
∴∠MPB=∠ABP,∠D=∠DPM=100°,
∴∠MPB=∠BPD+∠DPM=40°+100°=140°,
∴∠ABP=∠MPB=140°.
例2:已知,AB∥CD.
(1)如图1,求证:∠A-∠C=∠E;
(2)如图2,EF平分∠AEC,CF平分∠ECD,∠F=105°,求∠A的度数.
【解析】(1)证明: 过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠FEA=∠EAB,∠FEC=∠C,
∴∠AEC=∠FEA-∠FEC=∠EAB-∠C,即∠A-∠C=∠E.
(2)解:过点E作EG∥FC,
∵EF平分∠AEC,CF平分∠ECD,设∠AEF=∠CEF=,∠ECF=∠FCD=,
∵EG∥FC,
∴∠CEG=∠ECF=, ∠FEG+∠F=180°.
∵∠F=105°,
∴∠FEG=180°-∠F=75°,
∴∠CEG+∠CEF=75°,即 +=75°,
∴2x+2y=150°.
由(1)知,∠A=∠AEC+∠ECD=2x+2y=150°.
例3:已知直线∥,点A,B在直线上(B在A左侧),点C在直线b上,E点在直线b下方,连接 AE 交直线b于点D.
(1)如图1,若∠BAD=110°,∠DCE=45°,求∠DEC的度数;
(2)如图2,∠BAD 的邻补角的角平分线与∠DEC 的角平分线所在的直线交于点M,试探究∠AME与∠ECD之间的数量关系,并说明理由.
例4:已知AB∥CD.
(1)如图1,求证:∠EAB=∠C+∠E;
(2)如图2,点F在∠AEC内且在AB、CD之间,EF平分∠AEC,CF平分∠ECD,请猜想∠F与∠EAB的数量关系并证明;
(3)如图3,点M在AB上,点N在CD上,点E是AB上方一点,点G在AB、CD之间,连接EM、EN,GM的延长线MF平分∠AME,NE平分∠CNG,若2∠MEN+∠MGN=105°,求∠AME的度数.:
【解析】(1)过点E作EF∥DC,
∵BA∥DC,
∴EF∥DC∥AB,
∴∠AEF=∠BAE=110°,∠CEF=∠DCE=45°.
∴∠DEC=∠AEF-∠CEF=110°-45°=65°.
(2)过点M作MF∥BA,过点E作EG∥CD,设∠BAE=,∠ECD=,
∵BA∥CD,
∴MF∥AB∥CD∥EG.
∴∠BAE=∠AEG=,∠DCE=∠CEG=,
∴∠DEC=-.
∵EM平分∠DEC,AM平分∠BAD的邻补角,
∴∠MEC=,∠1==,
∵MF∥AB,
∴∠AMF=∠1=,∠MEG=∠CEG+∠MEC=,
∵MF∥EG,
∴∠FME=∠MEG=,
∴∠AME=∠AMF+∠FME=,
∴∠AME=.
模型四:“骨折”模型(也称“X射线”模型)
模型四“骨折”模型
点P在EF左侧,在AB、 CD外部 “骨折”模型
结论1:若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;
结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.
例1:如图,AB∥CD,∠E=40°,∠A=110°,则∠C的度数为70°.
解析:∵AB∥CD,
∴∠A+∠AFD=180°,
∵∠A=110°,
∴∠AFD=70°,
∴∠CFE=∠AFD=70°,
∵∠E=40°,∠C+∠E+∠CFE=180°,
∴∠C=180°﹣∠E﹣∠CFE=180°﹣40°﹣70°=70°,
故答案为:70°.
例2:如图,AB∥CD,∠ABE=125°,∠C=30°,则∠α=(D)
A.70° B.75° C.80° D.85°
【解析】解:如图,作EF∥AB,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠B+∠BEF=180°,∠C=∠CEF,
∵∠ABE=125°,∠C=30°,
∴∠BEF=55°,∠CEF=30°,
∴∠BEC=55°+30°=85°.故选:D.
例3:已知:如图,AB∥CD.
(1)若∠1=∠2,试判断∠E与∠F的大小关系,并说明你的理由.
(2)猜想∠1、∠2、∠E、∠F之间存在怎样的数量关系?并说明理由.
【解答】解:(1)∠E=∠F,理由如下:
∵AB∥CD,
∴∠ABC=∠BCD,
∵∠1=∠2,
∴∠EBC=∠FCB,
∴BE∥CF,
∴∠E=∠F;
(2)∠1+∠F=∠BEF+∠2,理由如下:
如图,延长BE交DC的延长线于点M,
在四边形EMCF中,∠FEM+∠EMC+∠MCF+∠F=360°,
∵∠FEM=180°﹣∠BEF,∠MCF=180°﹣∠2,
∴∠180°﹣∠BEF+∠EMC+180°﹣∠2+∠F=360°,
∵AB∥CD,
∴∠1=∠EMC,
∴∠180°﹣∠BEF+∠1+180°﹣∠2+∠F=360°,
∴∠1+∠F=∠BEF+∠2
例4:(1)(问题)如图1,若AB∥CD,∠AEP=40°,∠PFD=130°.求∠EPF的度数;
(2)(问题迁移)如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;
(3)(联想拓展)如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.
【解答】解:(1)如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°.(两直线平行,内错角相等)
∵AB∥CD,(已知)
∴PM∥CD,(平行于同一条直线的两直线平行)
∴∠2+∠PFD=180°. (两直线平行,同旁内角互补)
∵∠PFD=130°,
∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
(2)∠PFC=∠PEA+∠P.
理由:如图2,过P点作PN∥AB,则PN∥CD,
∴∠PEA=∠NPE,
∵∠FPN=∠NPE+∠FPE,
∴∠FPN=∠PEA+∠FPE,
∵PN∥CD,
∴∠FPN=∠PFC,
∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;
(3)如图,过点G作AB的平行线GH.
∵GH∥AB,AB∥CD,
∴GH∥AB∥CD,
∴∠HGE=∠AEG,∠HGF=∠CFG,
又∵∠PEA的平分线和∠PFC的平分线交于点G,
∴∠HGE=∠AEG=,∠HGF=∠CFG=,
由(1)可知,∠CFP=∠P+∠AEP,
∴∠HGF=(∠P+∠AEP)=(α+∠AEP),
∴∠EGF=∠HGF﹣∠HGE=(α+∠AEP)=+∠AEP﹣∠HGE=
例5:已知AB∥MN.
(1)如图1,求证:∠N+∠E=∠B;
(2)若F为直线MN、AB之间的一点,∠E=∠EFB,BG平分∠ABF交MN于点G,EF交MN于点C.
①如图2,若∠N=57°,且BG∥EN,求∠E的度数;
②如图3,若点K在射线BG上,且满足∠KNM=∠ENM,若∠NKB=∠EFB,∠E=∠FBD,直接写出∠E的度数.
【解答】解:(1)如图,
过E作EH∥MN,
∴∠N=∠HEN,
又∵MN∥AB,
∴EH∥AB∥MN,
∴∠B=∠HEB,
即∠B=∠HEN+∠NEB=∠N+∠BEN;
(2)①如图,
过F作FP∥EN,交MN于H点,则BG∥EN∥FP,
∵∠N=57°,
∴∠CHF=∠CGB=∠ABG=57°,
∵BG平分∠ABF,
∴∠ABF=2∠ABG=114°,
∵EN∥PF,
∴∠E=∠EFP,
∵∠E=∠EFB,
∴114°+∠E=4∠E,
∴∠E=38°;
②如图,过点F作FP∥AD,
设∠E=a=∠FBD,则∠PFB=α,∠EFP=3α,
∴∠ENM=2a,∠KNM=,
当K在BG上,∠NKB=∠EFB=4a,
∴∠NGB==∠ABG=∠GBF,
∴,
∴a=22.5°;
当K在BG延长线上时,∠NGB=,∠ABG=,
∴,
∴a=18°,
综上所述,∠E=22.5°或18°.
平面图形的认识(二):
专题:
平行线中的常见四大模型
专题:平行线中的常见模型
模型一:“猪蹄”模型(也称“M”模型)
模型一“猪蹄”模型(M模型)
点P在EF左侧,在AB、 CD内部 “猪蹄”模型
结论1:若AB∥CD,则∠P=∠AEP+∠CFP;
结论2:若∠P=∠AEP+∠CFP,则AB∥CD.
典型例题
例1:如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为( )
A.70° B.65° C.35° D.5°
例2:如图,AD∥CE,∠ABC=95°,则∠2﹣∠1的度数是( )
A.105° B.95° C.85° D.75°
例3:如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,求∠2的度数.
☆模型拓展:M叠M型
例4:如图,AB∥CD,∠E=35°,∠F=∠G=30°,则∠A+∠C的度数为 .
例5:如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )
A.30° B.35° C.40° D.45°
例6:如图,AB∥CD,∠E+∠G=∠H,则∠A+∠B+∠C+∠D+∠F的度数为 .
例7:如图,直线l1∥l2,点∠α、∠β夹在两平行线之间.
(1)若∠α=∠β,∠1=40°,求∠2的度数;
(2)直接写出∠1、∠2、∠α、∠β之间的数量关系,不用说明理由.
☆模型拓展:M套M型
例8:(1)如图1,已知AB∥CD,若∠EAF=∠EAB,∠ECF=∠ECD,
求证:∠AFC=∠AEC;
(2)如图2,若AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD,求证:∠AFC=∠AEC;
(3)若AB∥CD,∠EAF=∠EAB,∠ECF∠ECD,则∠AFC与∠AEC的数量关系是
(用含有n的代数式表示,不证明).
例9:如图①,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第1次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第2次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第3次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE1C=∠BEC;
(3)从图①开始进行上述的n次操作,若∠BEnC=α°,求∠BEC的大小(直接写出结论).
模型二:“铅笔”模型(也称“U”型模型)
模型二:“铅笔”模型(“U”型)
点P在EF右侧,在AB、 CD内部 “铅笔”模型
结论1:若AB∥CD,则∠P+∠AEP+∠PFC=360°;
结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD.
典型例题
例1:一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=135°,则∠ABC= 度.
例2:如图,直线l1∥l2,若∠1=35°,则∠2+∠3= .
例3:如图,已知AB∥CD,E为AB,CD之间一点,连接BE,DE.
(1)猜想∠BED时,∠B,∠D的数量关系,并证明;
(2)作∠ABE,∠CDE的角平分线BF,DF交于点F.
①依题意补全图形;②直接用等式表示∠BFD与∠BED的数量关系.
例4:如图,已知AB∥CD,∠ABE与∠CDE的平分线相交于点F.
(1)如图1,若∠E=70°,求∠BFD的度数;
(2)如图2,若∠ABM=∠ABF,∠CDM=∠CDF,写出∠M和∠E之间的数量关系,并证明你的结论.
例5:实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射的光线为n.
(1)当m∥n时,若∠1=50°,则∠2= ,∠3= ;
(2)当m∥n时,若∠1=x°(0<x<90),则∠3= ;
(3)根据(1)(2)结果,反过来猜想:当两平面镜a,b的夹角∠3为多少度时,m∥n.请说明理由(可以在图中添加适当的角度标记进行说明)
例6:如图,AB∥CD,点E为两直线之间的一点.
(1)如图1,若∠BAE=35°,∠DCE=20°,则∠AEC= ;
(2)如图2,试说明,∠BAE+∠AEC+∠ECD=360°;
(3)①如图3,若∠BAE的平分线与∠DCE的平分线相交于点F,判断∠AEC与∠AFC的数量关系,并说明理由;
②如图4,若设∠E=m,∠BAF=∠FAE,∠DCF=∠FCE,请直接用含m、n的代数式表示∠F的度数.
模型三:“抬头”模型(也称“靴子”或称“臭脚”模型)
模型三“抬头”模型(“靴子”模型)
点P在EF右侧,在AB、 CD外部 “靴子”模型
结论1:若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;
结论2:若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD.
典型例题
例1:如图,AB//CD,∠P=40°,∠D=100°,则∠ABP的度数是 .
例2:已知,AB∥CD.
(1)如图1,求证:∠A-∠C=∠E;
(2)如图2,EF平分∠AEC,CF平分∠ECD,∠F=105°,求∠A的度数.
例3:已知直线∥,点A,B在直线上(B在A左侧),点C在直线b上,E点在直线b下方,连接 AE 交直线b于点D.
(1)如图1,若∠BAD=110°,∠DCE=45°,求∠DEC的度数;
(2)如图2,∠BAD 的邻补角的角平分线与∠DEC 的角平分线所在的直线交于点M,试探究∠AME与∠ECD之间的数量关系,并说明理由.
例4:已知AB∥CD.
(1)如图1,求证:∠EAB=∠C+∠E;
(2)如图2,点F在∠AEC内且在AB、CD之间,EF平分∠AEC,CF平分∠ECD,请猜想∠F与∠EAB的数量关系并证明;
(3)如图3,点M在AB上,点N在CD上,点E是AB上方一点,点G在AB、CD之间,连接EM、EN,GM的延长线MF平分∠AME,NE平分∠CNG,若2∠MEN+∠MGN=105°,求∠AME的度数.:
模型四:“骨折”模型(也称“X射线”模型)
模型四“骨折”模型
点P在EF左侧,在AB、 CD外部 “骨折”模型
结论1:若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;
结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.
例1:如图,AB∥CD,∠E=40°,∠A=110°,则∠C的度数为 .
例2:如图,AB∥CD,∠ABE=125°,∠C=30°,则∠α=( )
A.70° B.75° C.80° D.85°
例3:已知:如图,AB∥CD.
(1)若∠1=∠2,试判断∠E与∠F的大小关系,并说明你的理由.
(2)猜想∠1、∠2、∠E、∠F之间存在怎样的数量关系?并说明理由.
例4:(1)(问题)如图1,若AB∥CD,∠AEP=40°,∠PFD=130°.求∠EPF的度数;
(2)(问题迁移)如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;
(3)(联想拓展)如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.
例5:已知AB∥MN.
(1)如图1,求证:∠N+∠E=∠B;
(2)若F为直线MN、AB之间的一点,∠E=∠EFB,BG平分∠ABF交MN于点G,EF交MN于点C.
①如图2,若∠N=57°,且BG∥EN,求∠E的度数;
②如图3,若点K在射线BG上,且满足∠KNM=∠ENM,若∠NKB=∠EFB,∠E=∠FBD,直接写出∠E的度数.
参考答案
专题四:平行线中的常见模型
模型一:“猪蹄”模型(也称“M”模型)
模型一“猪蹄”模型(M模型)
点P在EF左侧,在AB、 CD内部 “猪蹄”模型
结论1:若AB∥CD,则∠P=∠AEP+∠CFP;
结论2:若∠P=∠AEP+∠CFP,则AB∥CD.
典型例题
例1:如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为(B)
A.70° B.65° C.35° D.5°
解析:作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴AB∥DE∥CF,
∴∠1=∠BCF,∠FCE=∠2,
∵∠1=30°,∠2=35°,
∴∠BCF=30°,∠FCE=35°,
∴∠BCE=65°,故选:B.
例2:如图,AD∥CE,∠ABC=95°,则∠2﹣∠1的度数是(C)
A.105° B.95° C.85° D.75°
解析:如图,作BF∥AD,
∵AD∥CE,
∴AD∥BF∥EC,
∴∠1=∠3,∠4+∠2=180°,∠3+∠4=95°,
∴∠1+∠4=95°,∠2+∠4=180°,
∴∠2﹣∠1=85°.故选:C.
例3:如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,求∠2的度数.
解析:过点D作DG∥b,
∵a∥b,且DE⊥b,
∴DG∥a,
∴∠1=∠CDG=25°,∠GDE=∠3=90°
∴∠2=∠CDG+∠GDE=25°+90°=115°.
☆模型拓展:M叠M型
例4:如图,AB∥CD,∠E=35°,∠F=∠G=30°,则∠A+∠C的度数为35°.
解析:如图所示,延长AE,CG,交于点H,过H作HP∥AB,
∵AB∥CD,
∴PH∥CD,
∴∠A=∠AHP,∠C=∠CHP,
∴∠A+∠C=∠AHC,
∵∠F=∠CGF=30°,
∴EF∥CH,
∴∠AHC=∠AEF=35°,
∴∠A+∠C=35°,
故答案为:35°.
例5:如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )
A.30° B.35° C.40° D.45°
解析:分别过E,F作GE∥AB,FH∥AB,
∵AB∥CD,
∴AB∥GE∥FH∥CD,
∴∠1=∠A,∠2=∠C,∠GEF+∠HFE=180°,
∵∠E=120°,∠F=90°,
∴∠1+∠GEF+∠HFE+∠2=210°,
∴∠1+∠2=210°﹣180°=30°,
即∠A+∠C=30°,故选:A.
例6:如图,AB∥CD,∠E+∠G=∠H,则∠A+∠B+∠C+∠D+∠F的度数为360°.
解析:如图所示,延长AE,DG交于点Q,
由题可得,∠A+∠D=∠Q,∠B+∠H+∠C=360°,
又∵∠Q=∠AEF+∠DGF﹣∠F,
∴∠A+∠D=∠AEF+∠DGF﹣∠F,
即∠F=∠AEF+∠DGF﹣(∠A+∠D),
又∵∠AEF+∠DGF=∠H,
∴∠A+∠B+∠C+∠D+∠F=∠A+∠B+∠C+∠D+∠AEF+∠DGF﹣(∠A+∠D)
=∠B+∠C+∠H
=360°,故答案为:360°.
例7:如图,直线l1∥l2,点∠α、∠β夹在两平行线之间.
(1)若∠α=∠β,∠1=40°,求∠2的度数;
(2)直接写出∠1、∠2、∠α、∠β之间的数量关系,不用说明理由.
解析:(1)如图,延长AE交直线l2于点E,
∵l1∥l2,
∴∠3=∠1=40°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°﹣∠3=180°﹣40°=140°.
(2)∠1+∠2+∠β﹣○α=180°.
理由:∵l1∥l2,
∴∠3=∠1.
∵∠BED=180°﹣∠α,
∴∠3+∠2+∠β+180°﹣α=360°,即∠1+∠2+∠β﹣∠α=180°.
☆模型拓展:M套M型
例8:(1)如图1,已知AB∥CD,若∠EAF=∠EAB,∠ECF=∠ECD,
求证:∠AFC=∠AEC;
(2)如图2,若AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD,求证:∠AFC=∠AEC;
(3)若AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD,则∠AFC与∠AEC的数量关系是
(用含有n的代数式表示,不证明).
解:(1)如图1,连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=2x°,∠ECD=2y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+2x°+∠ACE+2y°=180°,
∴∠CAE+∠ACE=180°﹣(2x°+2y°),∠FAC+∠FCA=180°﹣(x°+y°),
∴∠AEC=180°﹣(∠CAE+∠ACE)
=180°﹣[180°﹣(2x°+2y°)]
=2x°+2y°,
=2(x°+y°),
∠AFC=180°﹣(∠FAC+∠FCA)
=180°﹣[180°﹣(x°+y°)]
=x°+y°,
∴∠AFC=∠AEC;
(2)如图2,连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=3x°,∠ECD=3y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+3x°+∠ACE+3y°=180°,
∴∠CAE+∠ACE=180°﹣(3x°+3y°),∠FAC+∠FCA=180°﹣(2x°+2y°),
∴∠AEC=180°﹣(∠CAE+∠ACE)
=180°﹣[180°﹣(3x°+3y°)]
=3x°+3y°
=3(x°+y°),
∠AFC=180°﹣(∠FAC+∠FCA)
=180°﹣[180°﹣(2x°+2y°)]
=2x°+2y°
=2(x°+y°),
∴∠AFC=∠AEC;
(3)若∠AFC=∠EAB,∠ECF=∠ECD,则∠AFC与∠AEC的数量关系是:∠AFC=∠AEC.
故答案为:∠AFC=∠AEC.
例9:如图①,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第1次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第2次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第3次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE1C=∠BEC;
(3)从图①开始进行上述的n次操作,若∠BEnC=α°,求∠BEC的大小(直接写出结论).
【解答】解:(1)如图①,过E作EF∥AB.
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2.
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
(2)如图2.∵∠ABE和∠DCE的平分线交点为E1,
∴由(1)可得,∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BEC;
(3)如图2.∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC;…
以此类推,∠En=∠BEC,
∴当∠En=α度时,∠BEC=2nα°
模型二:“铅笔”模型(也称“U”型模型)
模型二:“铅笔”模型(“U”型)
点P在EF右侧,在AB、 CD内部 “铅笔”模型
结论1:若AB∥CD,则∠P+∠AEP+∠PFC=360°;
结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD.
典型例题
例1:一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=135°,则∠ABC=135度.
【解析】解:如图,过点B作BF∥CD,
∵CD∥AE,
∴CD∥BF∥AE,
∴∠1+∠BCD=180°,∠2+∠BAE=180°,
∵∠BCD=135°,∠BAE=90°,
∴∠1=45°,∠2=90°,
∴∠ABC=∠1+∠2=135°.
故答案为:135.
例2:如图,直线l1∥l2,若∠1=35°,则∠2+∠3=215°.
【解析】解:过点E作EF∥11,
∵11∥12,EF∥11,
∴EF∥11∥12,
∴∠1=∠AEF=35°,∠FEC+∠3=180°,
∴∠2+∠3=∠AEF+∠FEC+∠3=35°+180°=215°.
故答案为:215°.
例3:如图,已知AB∥CD,E为AB,CD之间一点,连接BE,DE.
(1)猜想∠BED时,∠B,∠D的数量关系,并证明;
(2)作∠ABE,∠CDE的角平分线BF,DF交于点F.
①依题意补全图形;②直接用等式表示∠BFD与∠BED的数量关系.
【解析】(1)∠B+∠BED+∠D=360°.
证明:过点E作EG∥AB.
∴∠B+∠BEG=180°.
∵AB∥CD,EG∥AB,
∴EG∥CD,
∴∠DEG+∠D=180°,
∴∠B+∠BEG+∠DEG+∠D=180°+180°.
即∠B+∠BED+∠D=360°;
(2)解:①如图所示:
②由(1)得∠ABC+∠BED+∠CDE=360°,
∵∠ABE,∠CDE的角平分线BF,DF交于点F,
∴∠ABC=2∠FBE,∠CDE=2∠FDE,
∴2∠FBE+∠BED+2∠CDE=360°,即∠FBE+∠BED+∠CDE=180°,
∵∠BFD+∠FBE+∠BED+∠CDE=360°,
∴∠BFD=180°-∠BED
例4:如图,已知AB∥CD,∠ABE与∠CDE的平分线相交于点F.
(1)如图1,若∠E=70°,求∠BFD的度数;
(2)如图2,若∠ABM=∠ABF,∠CDM=∠CDF,写出∠M和∠E之间的数量关系,并证明你的结论.
【解析】解:(1)如图1,过点E作EN∥AB,
∵EN∥AB,
∴∠ABE+∠BEN=180°,
∵AB∥CD,AB∥NE,
∴NE∥CD,
∴∠CDE+∠NED=180°,
∴∠ABE+∠E+∠CDE=360°,
∵∠E=70°,
∴∠ABE+∠CDE=290°,
∵∠ABE与∠CDE的平分线相交于点F,
∴∠ABF+∠CDF=(∠ABE+∠CDE)=145°,
过点F作FG∥AB,
∵FG∥AB,
∴∠ABF=∠BFG,
∵AB∥CD,FG∥AB,
∴FG∥CD,
∴∠CDF=∠GFD,
∴∠BFD=∠ABF+∠CDF=145°;
(2)结论:∠E+6∠M=360°,
证明:∵设∠ABM=x,∠CDM=y,则∠FBM=2x,∠EBF=3x,∠FDM=2y,∠EDF=3y,
由(1)得:∠ABE+∠E+∠CDE=360°,
∴6x+6y+∠E=360°,
∵∠M+∠EBM+∠E+∠EDM=360°,
∴6x+6y+∠E=∠M+5x+5y+∠E,
∴∠M=x+y,
∴∠E+6∠M=360°.
例5:实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射的光线为n.
(1)当m∥n时,若∠1=50°,则∠2=100°,∠3= 90°;
(2)当m∥n时,若∠1=x°(0<x<90),则∠3= 90°;
(3)根据(1)(2)结果,反过来猜想:当两平面镜a,b的夹角∠3为多少度时,m∥n.请说明理由(可以在图中添加适当的角度标记进行说明)
【解析】解:(1)∵m∥n,
∴∠4+∠2=180°,
∵∠5=∠1=50°,
∴∠4=80°,
∴∠2=100°,
∴∠6=∠7=40°,
∴∠3=180°﹣∠5﹣∠6=90°,
故答案为:100°;90°;
(2)∵m∥n,
∴∠4+∠2=180°,
∵∠5=∠1=x°,
∴∠4=180°﹣2x°,
∴∠2=2x°,
∴∠6=∠7=90°﹣x°,
∴∠3=180°﹣∠5﹣∠6=180°﹣x°﹣90°+x°=90°,
故答案为:90°;
(3)根据(1)、(2)猜想:当两平面镜a、b的夹角∠3是90°时,总有m∥n,
证明:∵∠3=90°,
∴∠5+∠6=90°,
∴∠1+∠7=90°,
∴∠1+∠5+∠6+∠7=180°,
又∵∠1+∠4+∠5+∠2+∠6+∠7=360°,
∴∠4+∠2=180°,
∴m∥n.
例6:如图,AB∥CD,点E为两直线之间的一点.
(1)如图1,若∠BAE=35°,∠DCE=20°,则∠AEC=55°;
(2)如图2,试说明,∠BAE+∠AEC+∠ECD=360°;
(3)①如图3,若∠BAE的平分线与∠DCE的平分线相交于点F,判断∠AEC与∠AFC的数量关系,并说明理由;
②如图4,若设∠E=m,∠BAF=∠FAE,∠DCF=∠FCE,请直接用含m、n的代数式表示∠F的度数.
【解析】解:如图所示,过点E作EF∥AB,
∵AB∥CD∴AB∥CD∥EF,
∴∠BAE=∠1,∠ECD=∠2,
∴∠AEC=∠1+∠2=∠BAE+∠ECD=35°+20°=55°,
故答案为55°.
(2)如图所示,过点E作EG∥AB,
∵AB∥CD∴AB∥CD∥EG,
∴∠A+∠1=180°,∠C+∠2=180°,
∴∠A+∠1+∠2+∠C=360°,
即∠BAE+∠AEC+∠ECD=360°.
(3)①2∠AFC+∠AEC=360°,理由如下:
由(1)可得,∠AFC=∠BAF+∠DCF,
∵AF平分∠BAE,CF平分∠DCE,
∴∠BAE=2∠BAF,∠DCE=2∠DCF,
∴∠BAE+∠DCE=2∠AFC,
由(2)可知,∠BAE+∠AEC+∠DCE=360°,
∴2∠AFC+∠AEC=360°.
②由①知∠F+∠FAE+∠E+∠FCE=360°,
∵∠BAF=∠FAE,∠DCF=∠FCE,∠BAF+∠DCF=∠F,
∴∠F=(∠FAE+∠FCE),
∴∠FAE+∠FCE=n∠F,
∴∠F+∠E+n∠F=360°,
∴(n+1)∠F=360°﹣∠E=360°﹣m,
∴∠F=.
模型三:“抬头”模型(也称“靴子”或称“臭脚”模型)
模型三“抬头”模型(“靴子”模型)
点P在EF右侧,在AB、 CD外部 “靴子”模型
结论1:若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;
结论2:若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD.
典型例题
例1:如图,AB//CD,∠P=40°,∠D=100°,则∠ABP的度数是140°.
【解析】过点P作PM∥AB,
∵AB∥CD,
∴PM∥AB∥CD,
∴∠MPB=∠ABP,∠D=∠DPM=100°,
∴∠MPB=∠BPD+∠DPM=40°+100°=140°,
∴∠ABP=∠MPB=140°.
例2:已知,AB∥CD.
(1)如图1,求证:∠A-∠C=∠E;
(2)如图2,EF平分∠AEC,CF平分∠ECD,∠F=105°,求∠A的度数.
【解析】(1)证明: 过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠FEA=∠EAB,∠FEC=∠C,
∴∠AEC=∠FEA-∠FEC=∠EAB-∠C,即∠A-∠C=∠E.
(2)解:过点E作EG∥FC,
∵EF平分∠AEC,CF平分∠ECD,设∠AEF=∠CEF=,∠ECF=∠FCD=,
∵EG∥FC,
∴∠CEG=∠ECF=, ∠FEG+∠F=180°.
∵∠F=105°,
∴∠FEG=180°-∠F=75°,
∴∠CEG+∠CEF=75°,即 +=75°,
∴2x+2y=150°.
由(1)知,∠A=∠AEC+∠ECD=2x+2y=150°.
例3:已知直线∥,点A,B在直线上(B在A左侧),点C在直线b上,E点在直线b下方,连接 AE 交直线b于点D.
(1)如图1,若∠BAD=110°,∠DCE=45°,求∠DEC的度数;
(2)如图2,∠BAD 的邻补角的角平分线与∠DEC 的角平分线所在的直线交于点M,试探究∠AME与∠ECD之间的数量关系,并说明理由.
例4:已知AB∥CD.
(1)如图1,求证:∠EAB=∠C+∠E;
(2)如图2,点F在∠AEC内且在AB、CD之间,EF平分∠AEC,CF平分∠ECD,请猜想∠F与∠EAB的数量关系并证明;
(3)如图3,点M在AB上,点N在CD上,点E是AB上方一点,点G在AB、CD之间,连接EM、EN,GM的延长线MF平分∠AME,NE平分∠CNG,若2∠MEN+∠MGN=105°,求∠AME的度数.:
【解析】(1)过点E作EF∥DC,
∵BA∥DC,
∴EF∥DC∥AB,
∴∠AEF=∠BAE=110°,∠CEF=∠DCE=45°.
∴∠DEC=∠AEF-∠CEF=110°-45°=65°.
(2)过点M作MF∥BA,过点E作EG∥CD,设∠BAE=,∠ECD=,
∵BA∥CD,
∴MF∥AB∥CD∥EG.
∴∠BAE=∠AEG=,∠DCE=∠CEG=,
∴∠DEC=-.
∵EM平分∠DEC,AM平分∠BAD的邻补角,
∴∠MEC=,∠1==,
∵MF∥AB,
∴∠AMF=∠1=,∠MEG=∠CEG+∠MEC=,
∵MF∥EG,
∴∠FME=∠MEG=,
∴∠AME=∠AMF+∠FME=,
∴∠AME=.
模型四:“骨折”模型(也称“X射线”模型)
模型四“骨折”模型
点P在EF左侧,在AB、 CD外部 “骨折”模型
结论1:若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;
结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.
例1:如图,AB∥CD,∠E=40°,∠A=110°,则∠C的度数为70°.
解析:∵AB∥CD,
∴∠A+∠AFD=180°,
∵∠A=110°,
∴∠AFD=70°,
∴∠CFE=∠AFD=70°,
∵∠E=40°,∠C+∠E+∠CFE=180°,
∴∠C=180°﹣∠E﹣∠CFE=180°﹣40°﹣70°=70°,
故答案为:70°.
例2:如图,AB∥CD,∠ABE=125°,∠C=30°,则∠α=(D)
A.70° B.75° C.80° D.85°
【解析】解:如图,作EF∥AB,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠B+∠BEF=180°,∠C=∠CEF,
∵∠ABE=125°,∠C=30°,
∴∠BEF=55°,∠CEF=30°,
∴∠BEC=55°+30°=85°.故选:D.
例3:已知:如图,AB∥CD.
(1)若∠1=∠2,试判断∠E与∠F的大小关系,并说明你的理由.
(2)猜想∠1、∠2、∠E、∠F之间存在怎样的数量关系?并说明理由.
【解答】解:(1)∠E=∠F,理由如下:
∵AB∥CD,
∴∠ABC=∠BCD,
∵∠1=∠2,
∴∠EBC=∠FCB,
∴BE∥CF,
∴∠E=∠F;
(2)∠1+∠F=∠BEF+∠2,理由如下:
如图,延长BE交DC的延长线于点M,
在四边形EMCF中,∠FEM+∠EMC+∠MCF+∠F=360°,
∵∠FEM=180°﹣∠BEF,∠MCF=180°﹣∠2,
∴∠180°﹣∠BEF+∠EMC+180°﹣∠2+∠F=360°,
∵AB∥CD,
∴∠1=∠EMC,
∴∠180°﹣∠BEF+∠1+180°﹣∠2+∠F=360°,
∴∠1+∠F=∠BEF+∠2
例4:(1)(问题)如图1,若AB∥CD,∠AEP=40°,∠PFD=130°.求∠EPF的度数;
(2)(问题迁移)如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;
(3)(联想拓展)如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.
【解答】解:(1)如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°.(两直线平行,内错角相等)
∵AB∥CD,(已知)
∴PM∥CD,(平行于同一条直线的两直线平行)
∴∠2+∠PFD=180°. (两直线平行,同旁内角互补)
∵∠PFD=130°,
∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
(2)∠PFC=∠PEA+∠P.
理由:如图2,过P点作PN∥AB,则PN∥CD,
∴∠PEA=∠NPE,
∵∠FPN=∠NPE+∠FPE,
∴∠FPN=∠PEA+∠FPE,
∵PN∥CD,
∴∠FPN=∠PFC,
∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;
(3)如图,过点G作AB的平行线GH.
∵GH∥AB,AB∥CD,
∴GH∥AB∥CD,
∴∠HGE=∠AEG,∠HGF=∠CFG,
又∵∠PEA的平分线和∠PFC的平分线交于点G,
∴∠HGE=∠AEG=,∠HGF=∠CFG=,
由(1)可知,∠CFP=∠P+∠AEP,
∴∠HGF=(∠P+∠AEP)=(α+∠AEP),
∴∠EGF=∠HGF﹣∠HGE=(α+∠AEP)=+∠AEP﹣∠HGE=
例5:已知AB∥MN.
(1)如图1,求证:∠N+∠E=∠B;
(2)若F为直线MN、AB之间的一点,∠E=∠EFB,BG平分∠ABF交MN于点G,EF交MN于点C.
①如图2,若∠N=57°,且BG∥EN,求∠E的度数;
②如图3,若点K在射线BG上,且满足∠KNM=∠ENM,若∠NKB=∠EFB,∠E=∠FBD,直接写出∠E的度数.
【解答】解:(1)如图,
过E作EH∥MN,
∴∠N=∠HEN,
又∵MN∥AB,
∴EH∥AB∥MN,
∴∠B=∠HEB,
即∠B=∠HEN+∠NEB=∠N+∠BEN;
(2)①如图,
过F作FP∥EN,交MN于H点,则BG∥EN∥FP,
∵∠N=57°,
∴∠CHF=∠CGB=∠ABG=57°,
∵BG平分∠ABF,
∴∠ABF=2∠ABG=114°,
∵EN∥PF,
∴∠E=∠EFP,
∵∠E=∠EFB,
∴114°+∠E=4∠E,
∴∠E=38°;
②如图,过点F作FP∥AD,
设∠E=a=∠FBD,则∠PFB=α,∠EFP=3α,
∴∠ENM=2a,∠KNM=,
当K在BG上,∠NKB=∠EFB=4a,
∴∠NGB==∠ABG=∠GBF,
∴,
∴a=22.5°;
当K在BG延长线上时,∠NGB=,∠ABG=,
∴,
∴a=18°,
综上所述,∠E=22.5°或18°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
