湖南省娄底市2014-2015学年八年级下学期期末考试数学试题
文档属性
| 名称 | 湖南省娄底市2014-2015学年八年级下学期期末考试数学试题 | 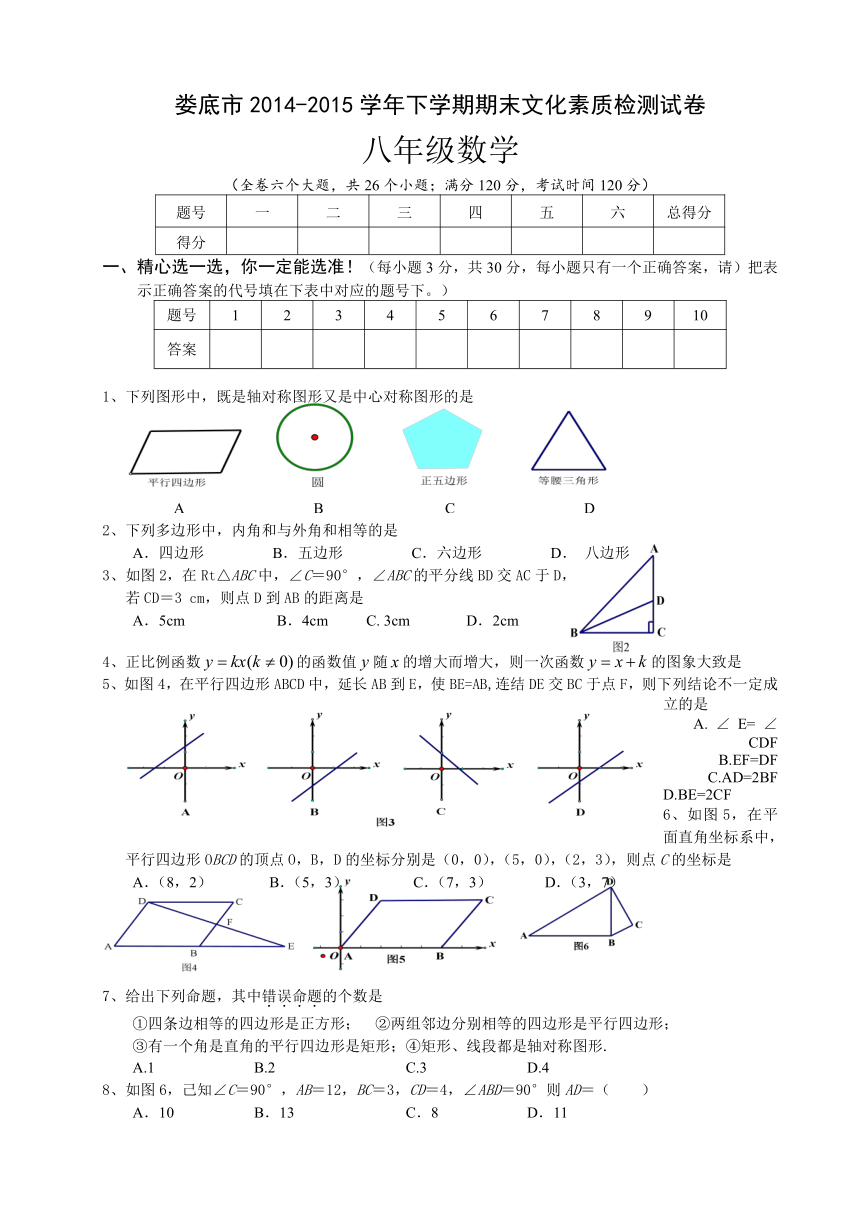 | |
| 格式 | zip | ||
| 文件大小 | 345.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-06 09:44:27 | ||
图片预览

文档简介
娄底市2014-2015学年下学期期末文化素质检测试卷
八年级数学
(全卷六个大题,共26个小题;满分120分,考试时间120分)
题号 一 二 三 四 五 六 总得分
得分
一、精心选一选,你一定能选准!(每小题3分,共30分,每小题只有一个正确答案,请)把表示正确答案的代号填在下表中对应的题号下。)
题号 1 2 3 4 5 6 7 8 9 10
答案
1、下列图形中,既是轴对称图形又是中心对称图形的是
2、下列多边形中,内角和与外角和相等的是
A.四边形 B.五边形 C.六边形 D. 八边形
如图2,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,
若CD=3 cm,则点D到AB的距离是
A.5cm B.4cm C. 3cm D.2cm
4、正比例函数的函数值随的增大而增大,则一次函数的图象大致是
5、如图4,在平行四边形ABCD中,延长AB到E,使BE=AB,连结DE交BC于点F,则下列结论不一定成立的是
A.∠E=∠CDF B.EF=DF C.AD=2BF D.BE=2CF
6、如图5,在平面直角坐标系中,平行四边形OBCD的顶点O,B,D的坐标分别是(0,0),(5,0),(2,3),则点C的坐标是
A.(8,2) B.(5,3) C.(7,3) D.(3,7)
7、给出下列命题,其中错误命题的个数是
①四条边相等的四边形是正方形; ②两组邻边分别相等的四边形是平行四边形;
③有一个角是直角的平行四边形是矩形;④矩形、线段都是轴对称图形.
A.1 B.2 C.3 D.4
8、如图6,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°则AD=( )
A.10 B.13 C.8 D.11
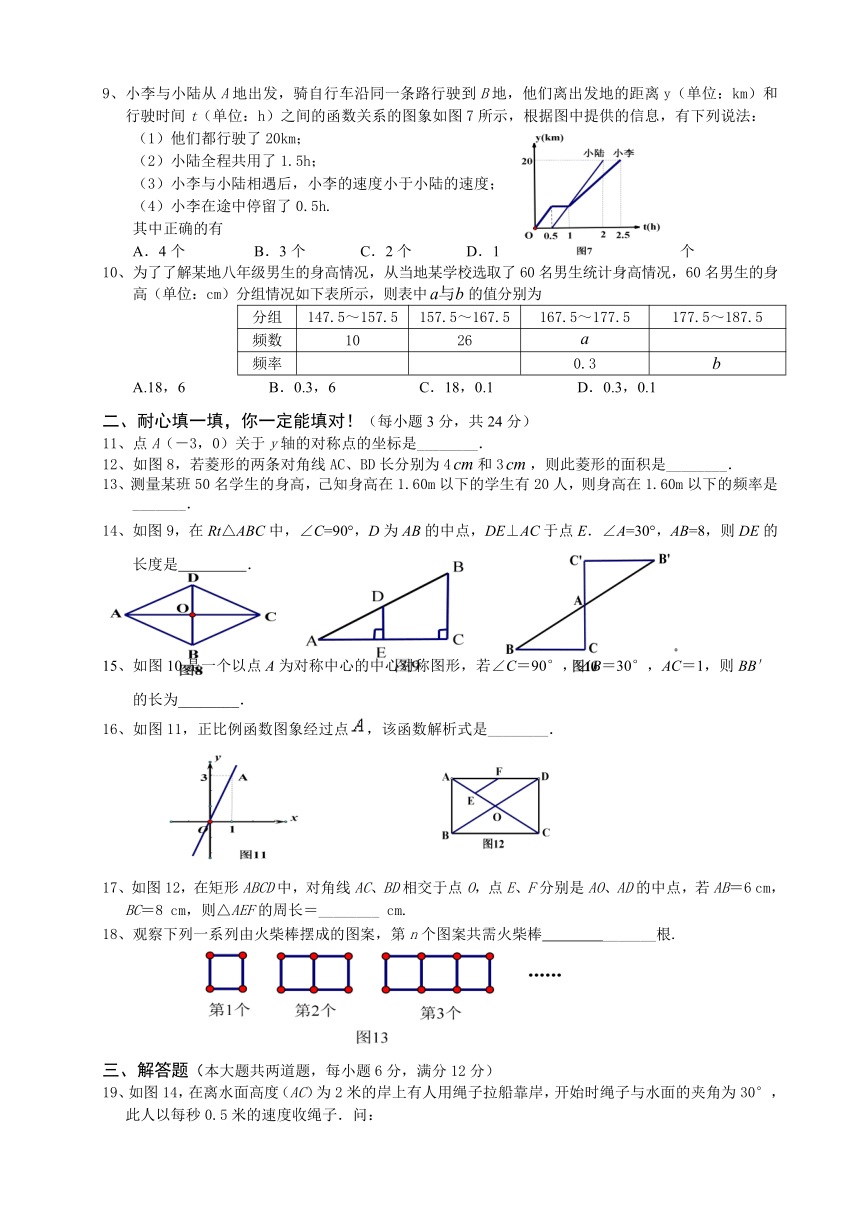
9、小李与小陆从A地出发,骑自行车沿同一 ( http: / / www.21cnjy.com )条路行驶到B地,他们离出发地的距离y(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图7所示,根据图中提供的信息,有下列说法:
(1)他们都行驶了20km;
(2)小陆全程共用了1.5h;
(3)小李与小陆相遇后,小李的速度小于小陆的速度;
(4)小李在途中停留了0.5h.
其中正确的有
A.4个 B.3个 C.2个 D.1个
10、为了了解某地八年级男生的身高情况,从当地某学校选取了60名男生统计身高情况,60名男生的身高(单位:cm)分组情况如下表所示,则表中的值分别为
分组 147.5~157.5 157.5~167.5 167.5~177.5 177.5~187.5
频数 10 26
频率 0.3
A.18,6 B.0.3,6 C.18,0.1 D.0.3,0.1
二、耐心填一填,你一定能填对!(每小题3分,共24分)
11、点A(-3,0)关于y轴的对称点的坐标是________.
12、如图8,若菱形的两条对角线AC、BD长分别为4和3,则此菱形的面积是________.
13、测量某班50名学生的身高,己知身高在1.60m以下的学生有20人,则身高在1.60m以下的频率是_______.
14、如图9,在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AC于点E.∠A=30°,AB=8,则DE的长度是 .
15、如图10是一个以点A为对称中心的中心对称图形,若∠C=90°,∠B=30°,AC=1,则BB′的长为________.
16、如图11,正比例函数图象经过点,该函数解析式是________.
17、如图12,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6 cm,BC=8 cm,则△AEF的周长=________ cm.
18、观察下列一系列由火柴棒摆成的图案,第n个图案共需火柴棒 _______根.
三、解答题(本大题共两道题,每小题6分,满分12分)
19、如图14,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米的速度收绳子.问:
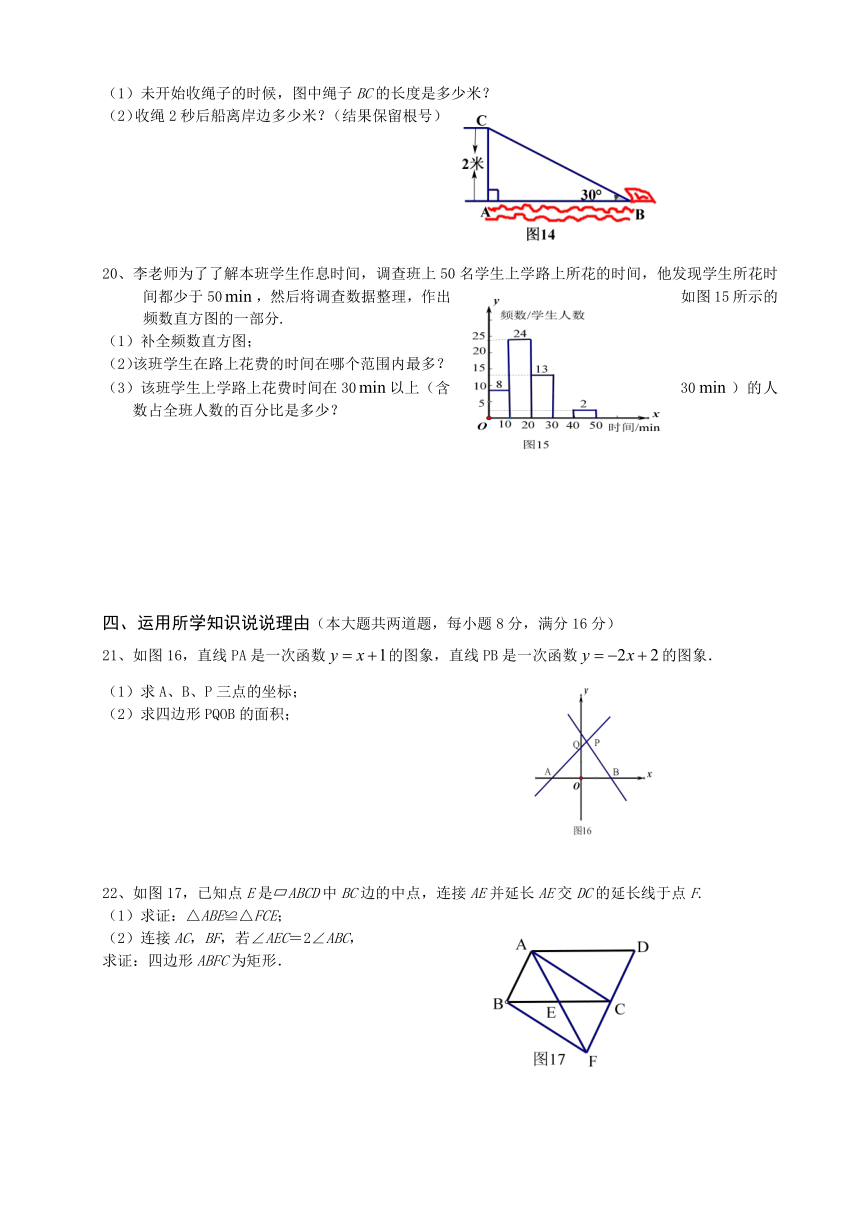
(1)未开始收绳子的时候,图中绳子BC的长度是多少米?
(2)收绳2秒后船离岸边多少米?(结果保留根号)
20、李老师为了了解本班学生作息时间,调查班上50名学生上学路上所花的时间,他发现学生所花时间都少于50,然后将调查数据整理,作出如图15所示的频数直方图的一部分.
(1)补全频数直方图;
(2)该班学生在路上花费的时间在哪个范围内最多?
(3)该班学生上学路上花费时间在30以上(含30)的人数占全班人数的百分比是多少?
四、运用所学知识说说理由(本大题共两道题,每小题8分,满分16分)
21、如图16,直线PA是一次函数的图象,直线PB是一次函数的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
22、如图17,已知点E是 ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)连接AC,BF,若∠AEC=2∠ABC,
求证:四边形ABFC为矩形.
五、学以致用(本大题共两道题,每小题9分,满分18分)
23、如图19,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上
(1)求线段AB所在直线的函数解析式;
(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有 个,在图上标出P点的位置.
24、某通讯公司推出(1)、(2)两种通讯 ( http: / / www.21cnjy.com )收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图18所示.
(Ⅰ)有月租费的收费方式是____(填(1)或(2)),月租费是________元;
(Ⅱ)分别求出(1)、(2)两种收费方式中y与自变量x之间的函数关系式;
(Ⅲ)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
六、操作与探究(本大题共两道题,每小题10,满分20分)
25、操作:准备一张长方形纸,按下图操作:
把矩形ABCD对折,得折痕MN.
(2)把A折向MN,得Rt△AEB
(3)沿线段EA折叠,得到另一条折痕EF,展开后可得到△EBF探究:△EBF的形状,
并说明理由.
26、已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,则CF,BC,CD三条线段之间有什么关系?并说明理由.
八年级下期未测试数学答案
1.B 2.A 3.C 4.A 5.D 6.C 7.B 8.B 9.B 10.C
11.(3,0) 12. 13.0.4 14.2 15.4 16.
17.9 18.
19.解:(1)如图,在Rt△ABC中,
∵∠CBA=30°,AC=2米
∴BC=2AC=2×2=4(米).……3分 第19题答图
(2)收绳2秒后,绳子BC缩短了1米,此时绳子只有3米,
即CD=3米,……4分
在Rt△ACD中,根据勾股定理得船到河岸的距离AD===(米),即收绳2秒后船离岸边 米. ……6分
20.解:(1)花费时间在范围内的频数为3,
在直方图上表示:略 ……2分
(2)花费时间在范围内的人数最多……4分
(3)10% ……6分
21.解:点A是直线AP与x轴的交点,所以A(-1,0……1分
Q点是直线AP与y轴的交点所以Q(0,1)……2分
又点B是直线BP与x轴的交点。所以B(1,0) ……3分
解方程组得所以点P……4分
因为A(-1,0),B(1,0)所以AB=2,
所以 ……8分
22.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,即AB∥CF.
∴∠BAE=∠CFE,∠ABE=∠FCE.
∵E是BC的中点,
∴BE=CE.
∴△ABE≌△FCE. ……4分
(2)∵△ABE≌△FCE,
∴AE=FE,BE=EC.
∴四边形ABCD是平行四边形.
∵∠AEC=∠ABC+∠BAE,
又∵∠AEC=2∠ABC,
∴∠ABE=∠BAE,
∴AE=BE,
即AF=BC.
∴四边形ABFC为矩形.……8分
23.解:(1)设直线AB的函数 解析式为y=kx+b(k、b为常数且k≠0)
依题意,得A(1,0),B(0,2)
,解得k=-2,b=2,
∴直线AB的函数解析式为y=-2x+2 ……6分
(2)如图,点P共有4个;……9分
24.解:(ⅰ)(1);30;……2分
(ⅱ)设y1=k1x+30,y2=k2x, ( http: / / www.21cnjy.com )由题意,将(500,80),(500,100)分别代入可得500k1+30=80,∴k1=0.1.
500k2=100,∴k2=0.2.
故所求的解析式为y1=0.1x+30,y2=0.2x. ……5分
(ⅲ)由y1=y2,得0.2x=0.1x+30,解得x=300.
当x=300时,y=60.
故由图可知当通话时间在300分钟内时,选择通话方式②实惠;
当通话时间超过300分钟时,选择通话方式①实惠;
当通话时间在300分钟时,
选择通话方式①、②一样实惠.……9分
25.△EBF是等边三角形 ……1分
理由:由操作(1)得M、N分别是AB、DC的中点
∴在Rt△ABE中,P为BE的中点,AP是斜边上的中线 ……3分
∴AP=BP=BE,即BE=2AP ……5分
在△EBF中,A是EF的中点,
∴AP=BF即BF=2AP ……7分
∴BE=BF
∴ ……8分
又,而 ……9分
∴
∴
∴△BEF为等边三角形 ……10分
26.解:(1)证明:∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°
∴AB=AC ……2分
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°.
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC
∴∠BAD=∠CAF
∵在△BA ( http: / / www.21cnjy.com )D和△CAF中,AB=AC,∠BAD=∠CAF,AD=AF,
∴△BAD≌△CAF(SAS)。∴BD=CF ……4分
∵BD+CD=BC,∴CF+CD=BC ……5分
(2) CF=BC+CD
理由:∵∠BAD=90o+∠CAD
∠CAF=90o+∠CAD
∴∠BAD=∠CAF
又∵AB=AC AD=AF
∴△BAD≌△CAF(SAS)
∴BD=CF 而BD=BC+CD
∴CF=BC+CD
A B C D
1
八年级数学
(全卷六个大题,共26个小题;满分120分,考试时间120分)
题号 一 二 三 四 五 六 总得分
得分
一、精心选一选,你一定能选准!(每小题3分,共30分,每小题只有一个正确答案,请)把表示正确答案的代号填在下表中对应的题号下。)
题号 1 2 3 4 5 6 7 8 9 10
答案
1、下列图形中,既是轴对称图形又是中心对称图形的是
2、下列多边形中,内角和与外角和相等的是
A.四边形 B.五边形 C.六边形 D. 八边形
如图2,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,
若CD=3 cm,则点D到AB的距离是
A.5cm B.4cm C. 3cm D.2cm
4、正比例函数的函数值随的增大而增大,则一次函数的图象大致是
5、如图4,在平行四边形ABCD中,延长AB到E,使BE=AB,连结DE交BC于点F,则下列结论不一定成立的是
A.∠E=∠CDF B.EF=DF C.AD=2BF D.BE=2CF
6、如图5,在平面直角坐标系中,平行四边形OBCD的顶点O,B,D的坐标分别是(0,0),(5,0),(2,3),则点C的坐标是
A.(8,2) B.(5,3) C.(7,3) D.(3,7)
7、给出下列命题,其中错误命题的个数是
①四条边相等的四边形是正方形; ②两组邻边分别相等的四边形是平行四边形;
③有一个角是直角的平行四边形是矩形;④矩形、线段都是轴对称图形.
A.1 B.2 C.3 D.4
8、如图6,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°则AD=( )
A.10 B.13 C.8 D.11
9、小李与小陆从A地出发,骑自行车沿同一 ( http: / / www.21cnjy.com )条路行驶到B地,他们离出发地的距离y(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图7所示,根据图中提供的信息,有下列说法:
(1)他们都行驶了20km;
(2)小陆全程共用了1.5h;
(3)小李与小陆相遇后,小李的速度小于小陆的速度;
(4)小李在途中停留了0.5h.
其中正确的有
A.4个 B.3个 C.2个 D.1个
10、为了了解某地八年级男生的身高情况,从当地某学校选取了60名男生统计身高情况,60名男生的身高(单位:cm)分组情况如下表所示,则表中的值分别为
分组 147.5~157.5 157.5~167.5 167.5~177.5 177.5~187.5
频数 10 26
频率 0.3
A.18,6 B.0.3,6 C.18,0.1 D.0.3,0.1
二、耐心填一填,你一定能填对!(每小题3分,共24分)
11、点A(-3,0)关于y轴的对称点的坐标是________.
12、如图8,若菱形的两条对角线AC、BD长分别为4和3,则此菱形的面积是________.
13、测量某班50名学生的身高,己知身高在1.60m以下的学生有20人,则身高在1.60m以下的频率是_______.
14、如图9,在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AC于点E.∠A=30°,AB=8,则DE的长度是 .
15、如图10是一个以点A为对称中心的中心对称图形,若∠C=90°,∠B=30°,AC=1,则BB′的长为________.
16、如图11,正比例函数图象经过点,该函数解析式是________.
17、如图12,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6 cm,BC=8 cm,则△AEF的周长=________ cm.
18、观察下列一系列由火柴棒摆成的图案,第n个图案共需火柴棒 _______根.
三、解答题(本大题共两道题,每小题6分,满分12分)
19、如图14,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米的速度收绳子.问:
(1)未开始收绳子的时候,图中绳子BC的长度是多少米?
(2)收绳2秒后船离岸边多少米?(结果保留根号)
20、李老师为了了解本班学生作息时间,调查班上50名学生上学路上所花的时间,他发现学生所花时间都少于50,然后将调查数据整理,作出如图15所示的频数直方图的一部分.
(1)补全频数直方图;
(2)该班学生在路上花费的时间在哪个范围内最多?
(3)该班学生上学路上花费时间在30以上(含30)的人数占全班人数的百分比是多少?
四、运用所学知识说说理由(本大题共两道题,每小题8分,满分16分)
21、如图16,直线PA是一次函数的图象,直线PB是一次函数的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
22、如图17,已知点E是 ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)连接AC,BF,若∠AEC=2∠ABC,
求证:四边形ABFC为矩形.
五、学以致用(本大题共两道题,每小题9分,满分18分)
23、如图19,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上
(1)求线段AB所在直线的函数解析式;
(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有 个,在图上标出P点的位置.
24、某通讯公司推出(1)、(2)两种通讯 ( http: / / www.21cnjy.com )收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图18所示.
(Ⅰ)有月租费的收费方式是____(填(1)或(2)),月租费是________元;
(Ⅱ)分别求出(1)、(2)两种收费方式中y与自变量x之间的函数关系式;
(Ⅲ)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
六、操作与探究(本大题共两道题,每小题10,满分20分)
25、操作:准备一张长方形纸,按下图操作:
把矩形ABCD对折,得折痕MN.
(2)把A折向MN,得Rt△AEB
(3)沿线段EA折叠,得到另一条折痕EF,展开后可得到△EBF探究:△EBF的形状,
并说明理由.
26、已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,则CF,BC,CD三条线段之间有什么关系?并说明理由.
八年级下期未测试数学答案
1.B 2.A 3.C 4.A 5.D 6.C 7.B 8.B 9.B 10.C
11.(3,0) 12. 13.0.4 14.2 15.4 16.
17.9 18.
19.解:(1)如图,在Rt△ABC中,
∵∠CBA=30°,AC=2米
∴BC=2AC=2×2=4(米).……3分 第19题答图
(2)收绳2秒后,绳子BC缩短了1米,此时绳子只有3米,
即CD=3米,……4分
在Rt△ACD中,根据勾股定理得船到河岸的距离AD===(米),即收绳2秒后船离岸边 米. ……6分
20.解:(1)花费时间在范围内的频数为3,
在直方图上表示:略 ……2分
(2)花费时间在范围内的人数最多……4分
(3)10% ……6分
21.解:点A是直线AP与x轴的交点,所以A(-1,0……1分
Q点是直线AP与y轴的交点所以Q(0,1)……2分
又点B是直线BP与x轴的交点。所以B(1,0) ……3分
解方程组得所以点P……4分
因为A(-1,0),B(1,0)所以AB=2,
所以 ……8分
22.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,即AB∥CF.
∴∠BAE=∠CFE,∠ABE=∠FCE.
∵E是BC的中点,
∴BE=CE.
∴△ABE≌△FCE. ……4分
(2)∵△ABE≌△FCE,
∴AE=FE,BE=EC.
∴四边形ABCD是平行四边形.
∵∠AEC=∠ABC+∠BAE,
又∵∠AEC=2∠ABC,
∴∠ABE=∠BAE,
∴AE=BE,
即AF=BC.
∴四边形ABFC为矩形.……8分
23.解:(1)设直线AB的函数 解析式为y=kx+b(k、b为常数且k≠0)
依题意,得A(1,0),B(0,2)
,解得k=-2,b=2,
∴直线AB的函数解析式为y=-2x+2 ……6分
(2)如图,点P共有4个;……9分
24.解:(ⅰ)(1);30;……2分
(ⅱ)设y1=k1x+30,y2=k2x, ( http: / / www.21cnjy.com )由题意,将(500,80),(500,100)分别代入可得500k1+30=80,∴k1=0.1.
500k2=100,∴k2=0.2.
故所求的解析式为y1=0.1x+30,y2=0.2x. ……5分
(ⅲ)由y1=y2,得0.2x=0.1x+30,解得x=300.
当x=300时,y=60.
故由图可知当通话时间在300分钟内时,选择通话方式②实惠;
当通话时间超过300分钟时,选择通话方式①实惠;
当通话时间在300分钟时,
选择通话方式①、②一样实惠.……9分
25.△EBF是等边三角形 ……1分
理由:由操作(1)得M、N分别是AB、DC的中点
∴在Rt△ABE中,P为BE的中点,AP是斜边上的中线 ……3分
∴AP=BP=BE,即BE=2AP ……5分
在△EBF中,A是EF的中点,
∴AP=BF即BF=2AP ……7分
∴BE=BF
∴ ……8分
又,而 ……9分
∴
∴
∴△BEF为等边三角形 ……10分
26.解:(1)证明:∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°
∴AB=AC ……2分
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°.
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC
∴∠BAD=∠CAF
∵在△BA ( http: / / www.21cnjy.com )D和△CAF中,AB=AC,∠BAD=∠CAF,AD=AF,
∴△BAD≌△CAF(SAS)。∴BD=CF ……4分
∵BD+CD=BC,∴CF+CD=BC ……5分
(2) CF=BC+CD
理由:∵∠BAD=90o+∠CAD
∠CAF=90o+∠CAD
∴∠BAD=∠CAF
又∵AB=AC AD=AF
∴△BAD≌△CAF(SAS)
∴BD=CF 而BD=BC+CD
∴CF=BC+CD
A B C D
1
同课章节目录
