寒假预习-3.2.1 圆锥的认识 人教版数学 六年级下册(含解析)
文档属性
| 名称 | 寒假预习-3.2.1 圆锥的认识 人教版数学 六年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 217.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 00:00:00 | ||
图片预览




文档简介
寒假预习-3.2.1 圆锥的认识
人教版数学 六年级下册
一、选择题
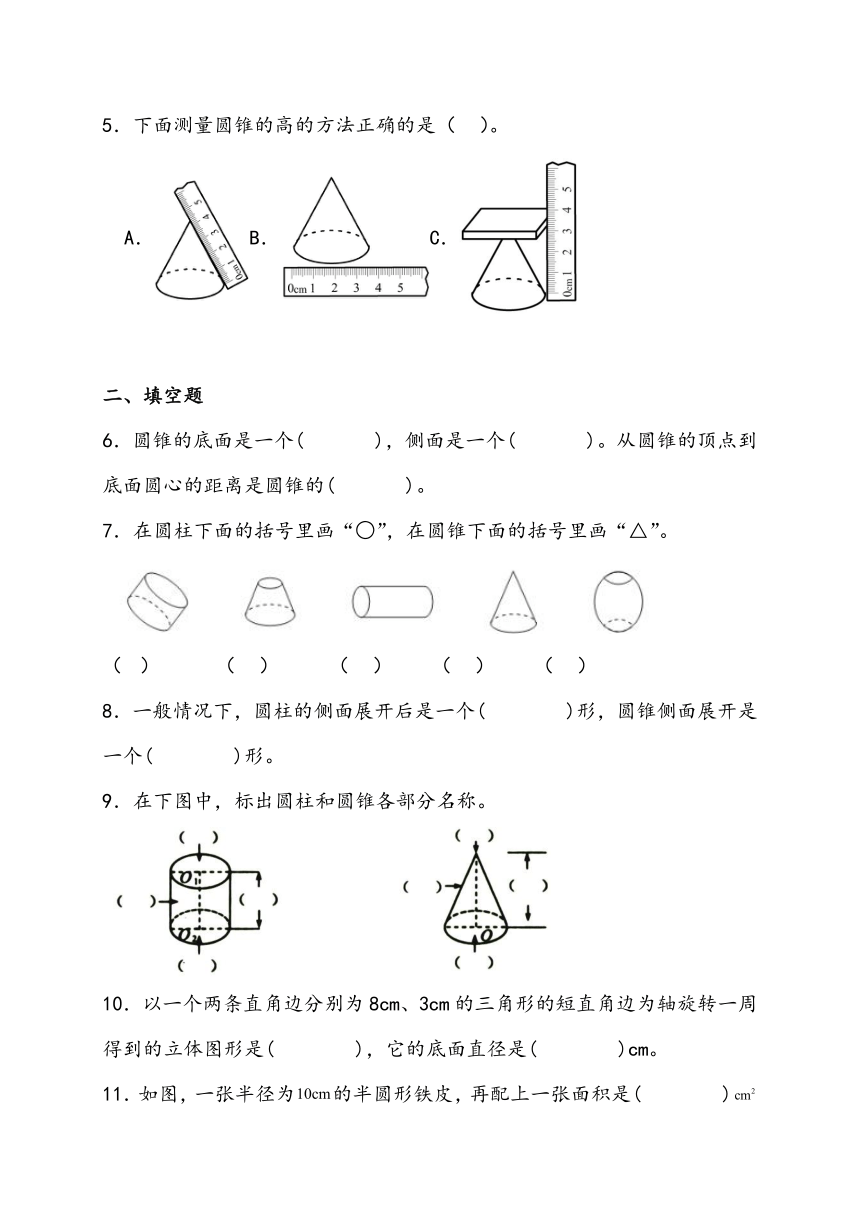
1.圆锥的侧面展开是一个( )。
A.长方形 B.正方形 C.扇形
2.下面选项中以虚线为轴旋转一周,( )能得到。
A. B. C.
3.下面图形以直线l为轴旋转一周形成的图形是( )。
A. B. C.
4.直角三角形ABC(如下图),以直角边AB为轴旋转360°后得到的是( )。
A.底面半径是8cm,高是6cm的圆锥
B.底面半径是6cm,高是8cm的圆锥
C.底面直径是6cm,高是8cm的圆锥
5.下面测量圆锥的高的方法正确的是( )。
A.B.C.
二、填空题
6.圆锥的底面是一个( ),侧面是一个( )。从圆锥的顶点到底面圆心的距离是圆锥的( )。
7.在圆柱下面的括号里画“○”,在圆锥下面的括号里画“△”。
( ) ( ) ( ) ( ) ( )
8.一般情况下,圆柱的侧面展开后是一个( )形,圆锥侧面展开是一个( )形。
9.在下图中,标出圆柱和圆锥各部分名称。
10.以一个两条直角边分别为8cm、3cm的三角形的短直角边为轴旋转一周得到的立体图形是( ),它的底面直径是( )cm。
11.如图,一张半径为的半圆形铁皮,再配上一张面积是( )的圆形铁皮刚好可以制成一个圆锥。(不考虑损耗)
12.一个圆锥的底面直径是4厘米,高是6厘米,沿底面直径将它切成完全相同的两部分,表面积增加( )平方厘米。
13.如下图,将直角三角形ABC的直角边AB所在直线为轴旋转一周,所得到立体图形是( ),底面积为( )cm2。
三、判断题
14.圆锥和圆柱一样,有无数条高。( )
15.图旋转一周可以得到。( )
16.从圆锥的顶点向底面作垂直切割,得到的截面是等腰三角形。 ( )
17.圆锥的侧面展开后是三角形。( )
18.锐角三角形绕一条边旋转一周,就会得到一个圆锥体。( )
四、解答题
19.把一个正方体木块加工成最大的圆锥体,它的底面半径是5厘米,这个正方体的体积是多少立方厘米?
20.以下图直角三角形的一条直角边所在直线为轴旋转一周,可以得到一个什么图形?所得的图形的底面直径和高各是多少厘米?
21.一个圆锥的底面半径2厘米,高是7厘米,沿着高并垂直于底面将圆锥切成完全相同的两块,每个切面的面积是多少平方厘米?
参考答案:
1.C
【分析】根据圆锥的特征,直接选出圆锥的侧面展开图即可。
【详解】圆锥的侧面展开是一个扇形。
故答案为:C
【点睛】本题考查了圆锥,圆锥的底面是圆,侧面是曲面,展开为扇形。
2.C
【分析】根据面动成体判断出各选项中的图形旋转得到的立体图形即可得解。
【详解】A.以虚线为轴旋转一周,则得到一个椭球,此选项不符合;
B.以虚线为轴旋转一周,则得到一个圆锥和一个圆柱的组合体,此选项不符合;
C.以虚线为轴旋转一周,则得到一个圆锥,此选项符合。
故答案为:C
【点睛】本题考查了点、线、面、体,熟悉并判断出旋转后的立体图形是解题的关键。
3.B
【分析】从已知的平面图形中可以看出,上面是长方形,下面是梯形;图形以直线l为轴旋转一周,形成立体图形,上面是圆柱,下面是圆台。
【详解】图形以直线l为轴旋转一周形成的图形是。
故答案为:B
【点睛】掌握平面图形旋转形成立体图形的方法是解题的关键。
4.B
【分析】根据题意,以一个直角三角形的直角边AB为轴旋转360°后得到的是圆锥,那么这条直角边AB是圆锥的高,另一条直角边BC是圆锥的底面半径。
【详解】以直角边AB为轴旋转360°后得到的是底面半径是6cm,高是8cm的圆锥。
故答案为:B
【点睛】掌握圆锥的特征以及应用是解题的关键。
5.C
【分析】圆锥的高指的是顶点高底面的距离,也就是顶点与底面圆圆心的连线,据此做出选择。
【详解】A.测量的是圆锥的母线长度,测量错误;
B.测量的是圆锥的底面直径,测量错误;
C.测量的是圆锥的高,测量正确;
故答案为:C
【点睛】平面几何中,高指的是点到线的距离,或线与线之间的距离;立体几何中,高指的是点到面的距离,或面与面之间的距离。
6. 圆 曲面 高
【详解】圆锥的底面是一个圆,侧面是一个曲面。从圆锥的顶点到底面圆心的距离是圆锥的高。
7.
【分析】根据圆柱的特征:圆柱的上、下底面是相等的圆,侧面是一个曲面,侧面展开的是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高;圆锥的特征,圆锥的底面是一个圆,侧面是一个曲面,圆锥的侧面展开图是一个扇形;据此判断即可。
【详解】由分析可知:第一个和第三个是圆柱,第四个是圆锥。
【点睛】本题考查的目的是理解掌握圆柱、圆锥的特征。
8. 长方 扇
【分析】根据圆柱的特征,它的上、下是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高;如果圆柱体的底面周长和高相等时,侧面展开是正方形,据此解答。
【详解】由分析可得:一般情况下,圆柱的侧面展开后是一个长方形,圆锥侧面展开是一个扇形。
【点睛】此题主要考查圆柱与圆锥的特征和它的侧面展开图的形状。
9.圆柱:底面 侧面 高 底面
圆锥:顶点 侧面 高 底面
【详解】圆柱和圆锥的特点,主要是从其形状、组成、面等方面来观察和研究的.圆柱的上下两个面是两个完全相同的圆,叫做底面.有一个面是曲面,叫做侧面,圆柱两底面之间的距离叫做圆柱的高。圆锥有一个顶点和两个面(一个底面是圆,一个曲面是侧面),从圆锥的顶点到底面圆心的距离叫做圆锥的高。
10. 圆锥 16
【分析】以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。较长的一条直角边是底面半径,进而确定底面直径。
【详解】8×2=16(cm)
以一个两条直角边分别为8cm、3cm的三角形的短直角边为轴旋转一周得到的立体图形是圆锥,它的底面直径是16cm。
【点睛】关键是熟悉圆锥的特征,圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高。
11.78.5
【分析】根据题意可知,圆周长的一半即为圆锥底面的周长,再根据“r=c÷π÷2”求出底面的半径,进而求出面积即可。
【详解】3.14×(2×10)÷2÷3.14÷2
=31.4÷3.14÷2
=5(厘米)
3.14×5 =78.5(平方厘米)
【点睛】明确圆周长的一半即为圆锥底面的周长是解答本题的关键。
12.24
【分析】沿圆锥底面直径将它切成完全相同的两部分,增加了两个等腰三角形,三角形的底=底面直径,三角形的高=圆锥的高,根据三角形面积=底×高÷2,求出一个切面面积,再乘2即可。
【详解】4×6÷2×2=24(平方厘米)
【点睛】关键是熟悉圆锥特征,掌握三角形面积公式。
13. 圆锥 28.26
【分析】如果以三角形直角边AB所在直线为轴旋转一周,其旋转所形成图形是一个圆锥体,圆锥体底面半径为3cm的圆,根据圆的面积公式:S=πr2,代入数据进行解答即可。
【详解】3.14×32
=3.14×9
=28.26(cm2)
所得到立体图形是圆锥,底面积为28.26cm2。
【点睛】此题主要考查了学生对圆锥底面积的计算。
14.×
【分析】根据圆柱的高和圆锥高的含义:圆柱的两个底面之间的距离,叫做圆柱的高,圆柱有无数条高;从圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥的高有1条;进行解答即可。
【详解】由分析可知:
圆柱有无数条高,圆锥只有1条高。所以原题干说法错误。
故答案为:×
【点睛】明确圆柱的特征和圆柱、圆锥高的含义,是解答此题的关键。
15.×
【分析】根据“点动成线,线动成面,面动成体”,图左边直线为轴旋转一周,可得到上面是球,下面是圆锥的立体图形。
【详解】图旋转一周可以得到。
原题说法错误。
故答案为:×
【点睛】此题考查了学生的空间想象能力。
16.√
【详解】从圆锥的顶点向底面作垂直切割后得到的三角形因为腰相等,故得到等腰三角形结论是正确的。
故答案为:√
17.×
【分析】圆锥是由一个圆形的底面和一个侧面组成的图形,侧面展开后是一个扇形。据此解答。
【详解】根据圆锥的特征可知:圆锥的侧面展开后是一个扇形;
故答案为:×。
【点睛】此题主要考查的是圆锥的特征,属于基础知识,要牢牢掌握。
18.×
【分析】锐角三角形绕一条边旋转一周,能得到两个圆锥体,这两个圆锥体共用一个底面积。
【详解】锐角三角形绕一条边旋转一周,就会得到两个圆锥体。原题错误。
故答案为:×
【点睛】本题考查圆锥,解答本题的关键是掌握以一个直角三角形的一条直角边为轴,另一条直角边为底面半径进行旋转一周,可得到圆锥。
19.1000立方厘米
【分析】由题干可知,把一个正方体木块加工成最大的圆锥体,圆锥体的底面直径等于正方体的棱长,再根据正方体的体积=棱长×棱长×棱长,即可解答。
【详解】由分析得,
5×2=10(厘米)
10×10×10
=100×10
=1000(立方厘米)
答:这个正方体的体积是1000立方厘米。
【点睛】此题考查的是立体图形的体积计算,解答此题要注意它们之间的内在联系。
20.圆锥;底面直径为16cm,高为6cm或 底面直径为12cm,高为8cm
【分析】直角三角形绕着一条直角边旋转一周可以得到一个圆锥,绕着旋转的直角边是圆锥的高,另一条直角边是底面半径,据此解答。
【详解】以直角三角形的一条直角边所在直线为轴旋转一周,可以得到一个圆锥。
(1)以6cm长的边所在直线为轴旋转
8×2=16(厘米)
底面直径是16厘米,高是6厘米。
(2)以8cm长的边所在直线为轴旋转
6×2=12(厘米)
底面直径是12厘米,高是8厘米。
答:以6cm长的边所在直线为轴旋转时,得到一个底面直径是16厘米,高是6厘米的圆锥,以8cm长的边所在直线为轴旋转时,得到一个底面直径是12厘米,高是8厘米的圆锥。
【点睛】以直角边所在的直线为轴旋转时该直角边就是圆锥的高,另一条直角边就是圆锥的底面半径。
21.14平方厘米
【分析】沿着高并垂直于底面将圆锥切成完全相同的两块,每一块的切面都是一个等腰三角形,而且这个三角形的底是圆锥底面直径,高是圆锥的高,也就是说底是4厘米,高是7厘米,所以每个切面的面积是14平方厘米。
【详解】2×2×7÷2=14(平方厘米)
答:每个切面的面积是14平方厘米。
【点睛】关键是熟悉圆锥特征,确定切面图形的形状。
人教版数学 六年级下册
一、选择题
1.圆锥的侧面展开是一个( )。
A.长方形 B.正方形 C.扇形
2.下面选项中以虚线为轴旋转一周,( )能得到。
A. B. C.
3.下面图形以直线l为轴旋转一周形成的图形是( )。
A. B. C.
4.直角三角形ABC(如下图),以直角边AB为轴旋转360°后得到的是( )。
A.底面半径是8cm,高是6cm的圆锥
B.底面半径是6cm,高是8cm的圆锥
C.底面直径是6cm,高是8cm的圆锥
5.下面测量圆锥的高的方法正确的是( )。
A.B.C.
二、填空题
6.圆锥的底面是一个( ),侧面是一个( )。从圆锥的顶点到底面圆心的距离是圆锥的( )。
7.在圆柱下面的括号里画“○”,在圆锥下面的括号里画“△”。
( ) ( ) ( ) ( ) ( )
8.一般情况下,圆柱的侧面展开后是一个( )形,圆锥侧面展开是一个( )形。
9.在下图中,标出圆柱和圆锥各部分名称。
10.以一个两条直角边分别为8cm、3cm的三角形的短直角边为轴旋转一周得到的立体图形是( ),它的底面直径是( )cm。
11.如图,一张半径为的半圆形铁皮,再配上一张面积是( )的圆形铁皮刚好可以制成一个圆锥。(不考虑损耗)
12.一个圆锥的底面直径是4厘米,高是6厘米,沿底面直径将它切成完全相同的两部分,表面积增加( )平方厘米。
13.如下图,将直角三角形ABC的直角边AB所在直线为轴旋转一周,所得到立体图形是( ),底面积为( )cm2。
三、判断题
14.圆锥和圆柱一样,有无数条高。( )
15.图旋转一周可以得到。( )
16.从圆锥的顶点向底面作垂直切割,得到的截面是等腰三角形。 ( )
17.圆锥的侧面展开后是三角形。( )
18.锐角三角形绕一条边旋转一周,就会得到一个圆锥体。( )
四、解答题
19.把一个正方体木块加工成最大的圆锥体,它的底面半径是5厘米,这个正方体的体积是多少立方厘米?
20.以下图直角三角形的一条直角边所在直线为轴旋转一周,可以得到一个什么图形?所得的图形的底面直径和高各是多少厘米?
21.一个圆锥的底面半径2厘米,高是7厘米,沿着高并垂直于底面将圆锥切成完全相同的两块,每个切面的面积是多少平方厘米?
参考答案:
1.C
【分析】根据圆锥的特征,直接选出圆锥的侧面展开图即可。
【详解】圆锥的侧面展开是一个扇形。
故答案为:C
【点睛】本题考查了圆锥,圆锥的底面是圆,侧面是曲面,展开为扇形。
2.C
【分析】根据面动成体判断出各选项中的图形旋转得到的立体图形即可得解。
【详解】A.以虚线为轴旋转一周,则得到一个椭球,此选项不符合;
B.以虚线为轴旋转一周,则得到一个圆锥和一个圆柱的组合体,此选项不符合;
C.以虚线为轴旋转一周,则得到一个圆锥,此选项符合。
故答案为:C
【点睛】本题考查了点、线、面、体,熟悉并判断出旋转后的立体图形是解题的关键。
3.B
【分析】从已知的平面图形中可以看出,上面是长方形,下面是梯形;图形以直线l为轴旋转一周,形成立体图形,上面是圆柱,下面是圆台。
【详解】图形以直线l为轴旋转一周形成的图形是。
故答案为:B
【点睛】掌握平面图形旋转形成立体图形的方法是解题的关键。
4.B
【分析】根据题意,以一个直角三角形的直角边AB为轴旋转360°后得到的是圆锥,那么这条直角边AB是圆锥的高,另一条直角边BC是圆锥的底面半径。
【详解】以直角边AB为轴旋转360°后得到的是底面半径是6cm,高是8cm的圆锥。
故答案为:B
【点睛】掌握圆锥的特征以及应用是解题的关键。
5.C
【分析】圆锥的高指的是顶点高底面的距离,也就是顶点与底面圆圆心的连线,据此做出选择。
【详解】A.测量的是圆锥的母线长度,测量错误;
B.测量的是圆锥的底面直径,测量错误;
C.测量的是圆锥的高,测量正确;
故答案为:C
【点睛】平面几何中,高指的是点到线的距离,或线与线之间的距离;立体几何中,高指的是点到面的距离,或面与面之间的距离。
6. 圆 曲面 高
【详解】圆锥的底面是一个圆,侧面是一个曲面。从圆锥的顶点到底面圆心的距离是圆锥的高。
7.
【分析】根据圆柱的特征:圆柱的上、下底面是相等的圆,侧面是一个曲面,侧面展开的是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高;圆锥的特征,圆锥的底面是一个圆,侧面是一个曲面,圆锥的侧面展开图是一个扇形;据此判断即可。
【详解】由分析可知:第一个和第三个是圆柱,第四个是圆锥。
【点睛】本题考查的目的是理解掌握圆柱、圆锥的特征。
8. 长方 扇
【分析】根据圆柱的特征,它的上、下是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高;如果圆柱体的底面周长和高相等时,侧面展开是正方形,据此解答。
【详解】由分析可得:一般情况下,圆柱的侧面展开后是一个长方形,圆锥侧面展开是一个扇形。
【点睛】此题主要考查圆柱与圆锥的特征和它的侧面展开图的形状。
9.圆柱:底面 侧面 高 底面
圆锥:顶点 侧面 高 底面
【详解】圆柱和圆锥的特点,主要是从其形状、组成、面等方面来观察和研究的.圆柱的上下两个面是两个完全相同的圆,叫做底面.有一个面是曲面,叫做侧面,圆柱两底面之间的距离叫做圆柱的高。圆锥有一个顶点和两个面(一个底面是圆,一个曲面是侧面),从圆锥的顶点到底面圆心的距离叫做圆锥的高。
10. 圆锥 16
【分析】以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。较长的一条直角边是底面半径,进而确定底面直径。
【详解】8×2=16(cm)
以一个两条直角边分别为8cm、3cm的三角形的短直角边为轴旋转一周得到的立体图形是圆锥,它的底面直径是16cm。
【点睛】关键是熟悉圆锥的特征,圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高。
11.78.5
【分析】根据题意可知,圆周长的一半即为圆锥底面的周长,再根据“r=c÷π÷2”求出底面的半径,进而求出面积即可。
【详解】3.14×(2×10)÷2÷3.14÷2
=31.4÷3.14÷2
=5(厘米)
3.14×5 =78.5(平方厘米)
【点睛】明确圆周长的一半即为圆锥底面的周长是解答本题的关键。
12.24
【分析】沿圆锥底面直径将它切成完全相同的两部分,增加了两个等腰三角形,三角形的底=底面直径,三角形的高=圆锥的高,根据三角形面积=底×高÷2,求出一个切面面积,再乘2即可。
【详解】4×6÷2×2=24(平方厘米)
【点睛】关键是熟悉圆锥特征,掌握三角形面积公式。
13. 圆锥 28.26
【分析】如果以三角形直角边AB所在直线为轴旋转一周,其旋转所形成图形是一个圆锥体,圆锥体底面半径为3cm的圆,根据圆的面积公式:S=πr2,代入数据进行解答即可。
【详解】3.14×32
=3.14×9
=28.26(cm2)
所得到立体图形是圆锥,底面积为28.26cm2。
【点睛】此题主要考查了学生对圆锥底面积的计算。
14.×
【分析】根据圆柱的高和圆锥高的含义:圆柱的两个底面之间的距离,叫做圆柱的高,圆柱有无数条高;从圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥的高有1条;进行解答即可。
【详解】由分析可知:
圆柱有无数条高,圆锥只有1条高。所以原题干说法错误。
故答案为:×
【点睛】明确圆柱的特征和圆柱、圆锥高的含义,是解答此题的关键。
15.×
【分析】根据“点动成线,线动成面,面动成体”,图左边直线为轴旋转一周,可得到上面是球,下面是圆锥的立体图形。
【详解】图旋转一周可以得到。
原题说法错误。
故答案为:×
【点睛】此题考查了学生的空间想象能力。
16.√
【详解】从圆锥的顶点向底面作垂直切割后得到的三角形因为腰相等,故得到等腰三角形结论是正确的。
故答案为:√
17.×
【分析】圆锥是由一个圆形的底面和一个侧面组成的图形,侧面展开后是一个扇形。据此解答。
【详解】根据圆锥的特征可知:圆锥的侧面展开后是一个扇形;
故答案为:×。
【点睛】此题主要考查的是圆锥的特征,属于基础知识,要牢牢掌握。
18.×
【分析】锐角三角形绕一条边旋转一周,能得到两个圆锥体,这两个圆锥体共用一个底面积。
【详解】锐角三角形绕一条边旋转一周,就会得到两个圆锥体。原题错误。
故答案为:×
【点睛】本题考查圆锥,解答本题的关键是掌握以一个直角三角形的一条直角边为轴,另一条直角边为底面半径进行旋转一周,可得到圆锥。
19.1000立方厘米
【分析】由题干可知,把一个正方体木块加工成最大的圆锥体,圆锥体的底面直径等于正方体的棱长,再根据正方体的体积=棱长×棱长×棱长,即可解答。
【详解】由分析得,
5×2=10(厘米)
10×10×10
=100×10
=1000(立方厘米)
答:这个正方体的体积是1000立方厘米。
【点睛】此题考查的是立体图形的体积计算,解答此题要注意它们之间的内在联系。
20.圆锥;底面直径为16cm,高为6cm或 底面直径为12cm,高为8cm
【分析】直角三角形绕着一条直角边旋转一周可以得到一个圆锥,绕着旋转的直角边是圆锥的高,另一条直角边是底面半径,据此解答。
【详解】以直角三角形的一条直角边所在直线为轴旋转一周,可以得到一个圆锥。
(1)以6cm长的边所在直线为轴旋转
8×2=16(厘米)
底面直径是16厘米,高是6厘米。
(2)以8cm长的边所在直线为轴旋转
6×2=12(厘米)
底面直径是12厘米,高是8厘米。
答:以6cm长的边所在直线为轴旋转时,得到一个底面直径是16厘米,高是6厘米的圆锥,以8cm长的边所在直线为轴旋转时,得到一个底面直径是12厘米,高是8厘米的圆锥。
【点睛】以直角边所在的直线为轴旋转时该直角边就是圆锥的高,另一条直角边就是圆锥的底面半径。
21.14平方厘米
【分析】沿着高并垂直于底面将圆锥切成完全相同的两块,每一块的切面都是一个等腰三角形,而且这个三角形的底是圆锥底面直径,高是圆锥的高,也就是说底是4厘米,高是7厘米,所以每个切面的面积是14平方厘米。
【详解】2×2×7÷2=14(平方厘米)
答:每个切面的面积是14平方厘米。
【点睛】关键是熟悉圆锥特征,确定切面图形的形状。
