5.3 平行线的性质 同步练习(含解析)
文档属性
| 名称 | 5.3 平行线的性质 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 301.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 13:25:14 | ||
图片预览


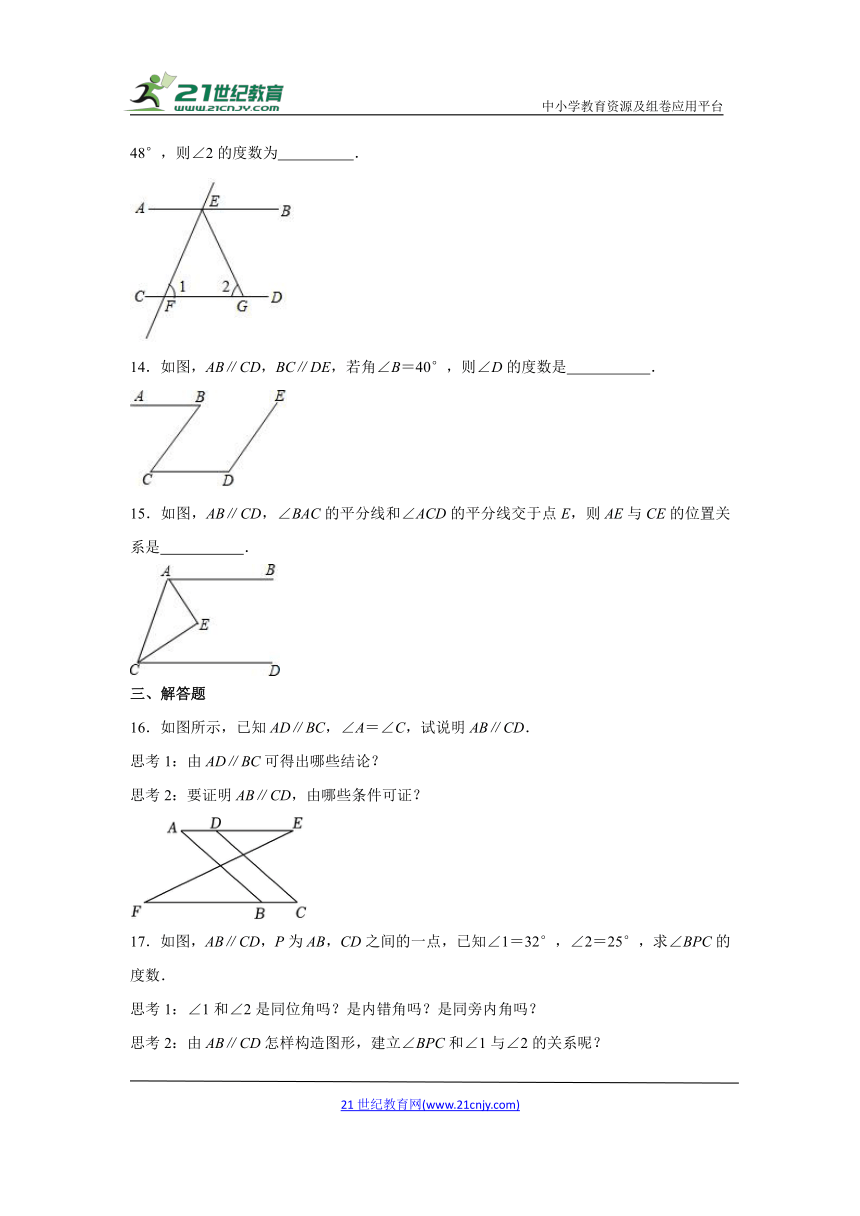
文档简介
中小学教育资源及组卷应用平台
人教新版七年级下册《5.3 平行线的性质》同步练习
一、选择题
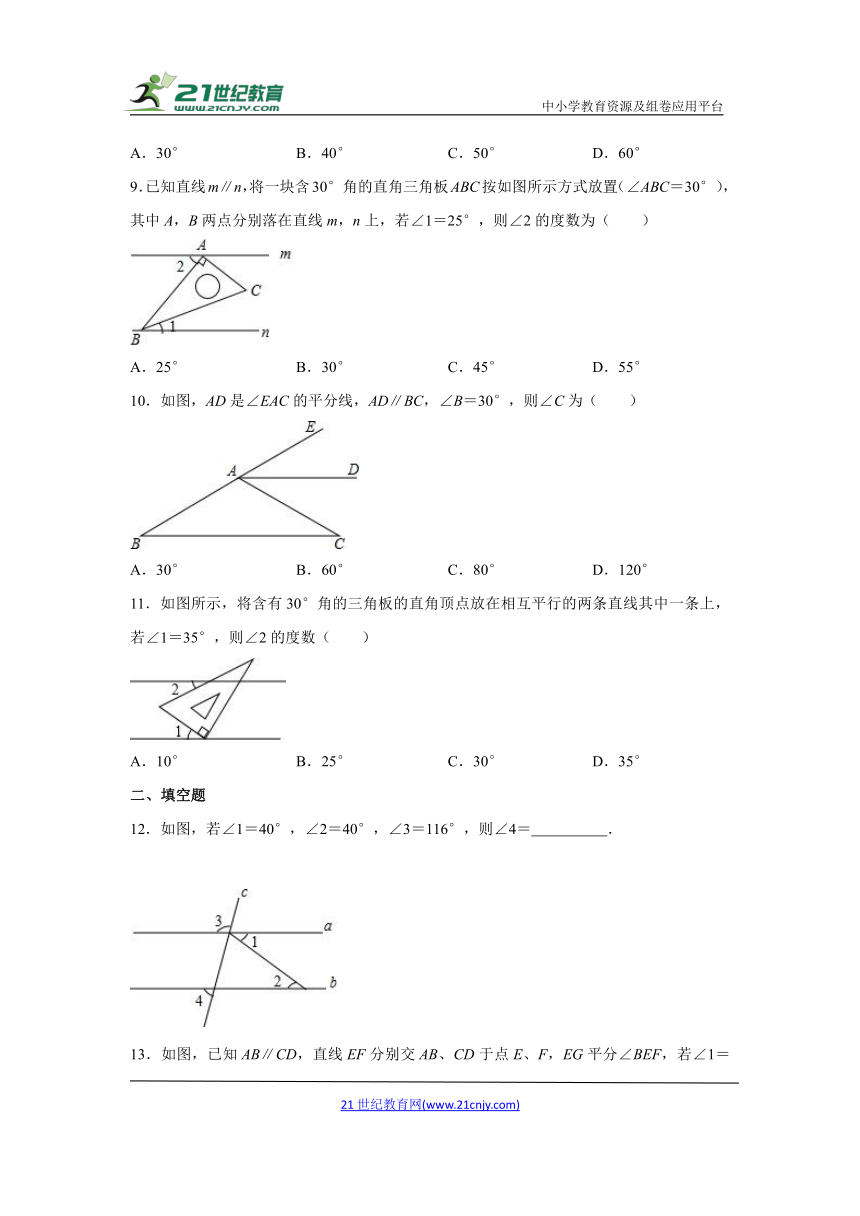
1.如图,AB∥CD,∠1=50°,∠2的度数是( )
A.50° B.100° C.130° D.140°
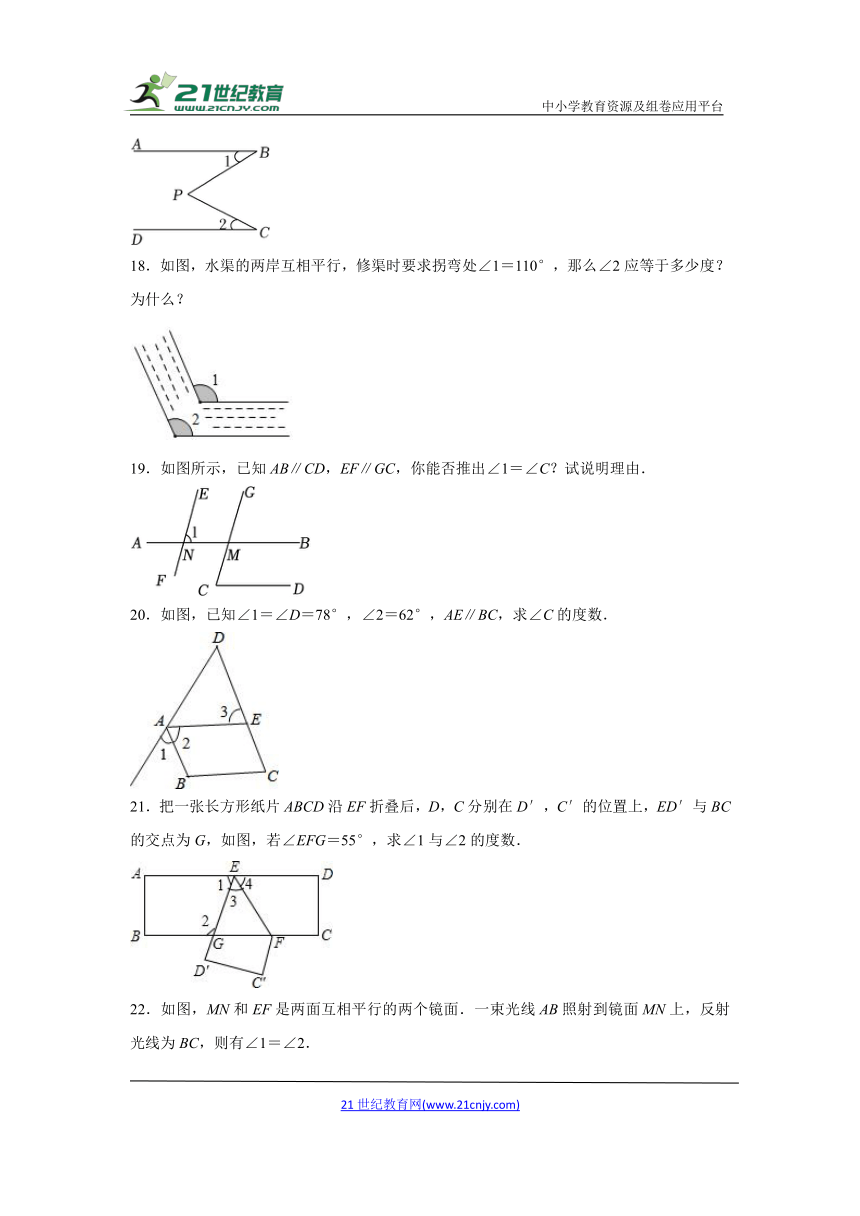
2.如图所示,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
3.如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
A.110° B.115° C.120° D.125°
4.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=50°,那么∠2的度数是( )
A.20° B.30° C.40° D.50°
5.如图,直线a∥b,直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=55°,则∠2的度数是( )
A.50° B.70° C.80° D.110°
6.如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )
A.30° B.32° C.42° D.58°
7.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是( )
A.90° B.110° C.120° D.150°
8.如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是( )
A.30° B.40° C.50° D.60°
9.已知直线m∥n,将一块含30°角的直角三角板ABC按如图所示方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=25°,则∠2的度数为( )
A.25° B.30° C.45° D.55°
10.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B.60° C.80° D.120°
11.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数( )
A.10° B.25° C.30° D.35°
二、填空题
12.如图,若∠1=40°,∠2=40°,∠3=116°,则∠4= .
13.如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=48°,则∠2的度数为 .
14.如图,AB∥CD,BC∥DE,若角∠B=40°,则∠D的度数是 .
15.如图,AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则AE与CE的位置关系是 .
三、解答题
16.如图所示,已知AD∥BC,∠A=∠C,试说明AB∥CD.
思考1:由AD∥BC可得出哪些结论?
思考2:要证明AB∥CD,由哪些条件可证?
17.如图,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,求∠BPC的度数.
思考1:∠1和∠2是同位角吗?是内错角吗?是同旁内角吗?
思考2:由AB∥CD怎样构造图形,建立∠BPC和∠1与∠2的关系呢?
18.如图,水渠的两岸互相平行,修渠时要求拐弯处∠1=110°,那么∠2应等于多少度?为什么?
19.如图所示,已知AB∥CD,EF∥GC,你能否推出∠1=∠C?试说明理由.
20.如图,已知∠1=∠D=78°,∠2=62°,AE∥BC,求∠C的度数.
21.把一张长方形纸片ABCD沿EF折叠后,D,C分别在D′,C′的位置上,ED′与BC的交点为G,如图,若∠EFG=55°,求∠1与∠2的度数.
22.如图,MN和EF是两面互相平行的两个镜面.一束光线AB照射到镜面MN上,反射光线为BC,则有∠1=∠2.
(1)画出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
人教新版七年级下册《5.3 平行线的性质》2024年同步练习卷(5)
参考答案与试题解析
一、选择题
1.如图,AB∥CD,∠1=50°,∠2的度数是( )
A.50° B.100° C.130° D.140°
【解答】解:∵AB∥CD,
∴∠3=∠1=50°,
∴∠2=180°﹣∠3=130°.
故选:C.
2.如图所示,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
【解答】解:∵∠1+∠5=180°,∠1+∠2=180°,
∴∠2=∠5,
∴a∥b,
∴∠3=∠6=100°,
∴∠4=100°.
故选:D.
3.如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
A.110° B.115° C.120° D.125°
【解答】解:∵∠1=∠2,
∴l1∥l2,
∴∠4=∠2+∠3,
∵∠2=∠3=55°,
∴∠4=110°,
故选:A.
4.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=50°,那么∠2的度数是( )
A.20° B.30° C.40° D.50°
【解答】解:∵AB⊥BC,
∴∠ABC=90°,
∴∠3=180°﹣90°﹣∠1=40°,
∵a∥b,
∴∠2=∠3=40°.
故选:C.
5.如图,直线a∥b,直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=55°,则∠2的度数是( )
A.50° B.70° C.80° D.110°
【解答】解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵a∥b,∠1=55°,
∴∠BAD=∠CAD=55°,
∴∠2=180°﹣55°﹣55°=70°.
故选:B.
6.如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )
A.30° B.32° C.42° D.58°
【解答】解:如图,
过点A作AB∥b,
∴∠3=∠1=58°,
∵∠3+∠4=90°,
∴∠4=90°﹣∠3=32°,
∵a∥b,AB∥b,
∴AB∥a,
∴∠2=∠4=32°,
故选:B.
7.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是( )
A.90° B.110° C.120° D.150°
【解答】解:延长FE交DC于点N,
∵直线AB∥EF,
∴∠BCD=∠DNF=95°,
∵∠CDE=25°,
∴∠DEF=95°+25°=120°.
故选:C.
8.如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是( )
A.30° B.40° C.50° D.60°
【解答】解:∵AB∥EF,
∴∠A=∠2=50°,
∵AC∥DF,
∴∠1=∠A=50°.
故选:C.
9.已知直线m∥n,将一块含30°角的直角三角板ABC按如图所示方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=25°,则∠2的度数为( )
A.25° B.30° C.45° D.55°
【解答】解:∵∠ABC=30°,∠1=25°,
∴∠ABD=∠1+∠ABC=55°,
∵直线m∥n,
∴∠2=∠ABD=55°,
故选:D.
10.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B.60° C.80° D.120°
【解答】解:∵AD∥BC,∠B=30°,
∴∠EAD=∠B=30°,
∵AD是∠EAC的平分线,
∴∠EAC=2∠EAD=2×30°=60°,
∴∠C=∠EAC﹣∠B=60°﹣30°=30°.
故选:A.
11.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数( )
A.10° B.25° C.30° D.35°
【解答】解:如图,延长AB交CF于E,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵∠1=35°,
∴∠AEC=∠ABC﹣∠1=25°,
∵GH∥EF,
∴∠2=∠AEC=25°,
故选:B.
二、填空题
12.如图,若∠1=40°,∠2=40°,∠3=116°,则∠4= 64° .
【解答】解:∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴a∥b,
∴∠5=∠3=116°,
∴∠4=180°﹣∠3=64°
故答案为:64°.
13.如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=48°,则∠2的度数为 66° .
【解答】解:∵AB∥CD,
∴∠BEF+∠1=180°,∠BEG=∠2,
∵∠1=48°,
∴∠BEF=132°,
∵EG平分∠BEF,
∴∠BEG=66°,
∴∠2=66°,
故答案为:66°.
14.如图,AB∥CD,BC∥DE,若角∠B=40°,则∠D的度数是 140° .
【解答】解:∵AB∥CD,∠B=40°,
∴∠C=∠B=40°,
∵BC∥DE,
∴∠C+∠D=180°,
∴∠D=140°.
故答案为140°.
15.如图,AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则AE与CE的位置关系是 互相垂直 .
【解答】解:∵AB∥CD,
∴∠BAC+∠ACD=180°.
∵∠BAC的平分线和∠ACD的平分线交于点E,
∴∠EAC+∠ACE=(∠BAC+∠ACD)=90°,
∴∠AEC=180°﹣90°=90°,
∴AE与CE互相垂直.
故答案为:互相垂直.
三、解答题
16.如图所示,已知AD∥BC,∠A=∠C,试说明AB∥CD.
思考1:由AD∥BC可得出哪些结论?
思考2:要证明AB∥CD,由哪些条件可证?
【解答】解:思考1:由AD∥BC可得出∠A=∠ABF,∠A+∠ABC=180°,∠EDC=∠C,∠E=∠F,∠ADC+∠C=180°;
思考2:要证明AB∥CD,需证明∠ABF=∠C,∠A=∠CDE,∠A+∠ADC=180°,∠C+∠ABC=180°.
17.如图,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,求∠BPC的度数.
思考1:∠1和∠2是同位角吗?是内错角吗?是同旁内角吗?
思考2:由AB∥CD怎样构造图形,建立∠BPC和∠1与∠2的关系呢?
【解答】解:思考1:根据同位角、内错角、同旁内角的定义,∠1和∠2不是由两条直线被第三条直线所截形成的角,故∠1和∠2不是同位角,不是内错角,不是同旁内角;
思考2:过点P作PN∥AB,
∵AB∥CD,
∴PN∥CD,
∴∠1=∠3=32°,∠2=∠4=25°,
∴∠BPC=∠3+∠4=∠1+∠2=32°+25°=57°.
18.如图,水渠的两岸互相平行,修渠时要求拐弯处∠1=110°,那么∠2应等于多少度?为什么?
【解答】解:∠2=110°,理由如下:
如图,过点A、D作射线AH,
∵AB∥DM,AC∥DN,
∴∠BAH=∠MDH,∠CAH=∠NDH,
∴∠BAH+∠CAH=∠MDH+∠NDH,
即∠2=∠1,
∵∠1=110°,
∴∠2=110°.
19.如图所示,已知AB∥CD,EF∥GC,你能否推出∠1=∠C?试说明理由.
【解答】解:能推出∠1=∠C;
理由如下:∵AB∥CD,
∴∠C=∠CMB,
∵EF∥GC,
∴∠1=∠CMB,
∴∠1=∠C.
20.如图,已知∠1=∠D=78°,∠2=62°,AE∥BC,求∠C的度数.
【解答】解:∵∠1=∠D=78°,
∴AB∥CD,
∵∠2=62°,
∴∠3=∠2=62°,
∵AE∥BC,
∴∠C=∠3=62°
21.把一张长方形纸片ABCD沿EF折叠后,D,C分别在D′,C′的位置上,ED′与BC的交点为G,如图,若∠EFG=55°,求∠1与∠2的度数.
【解答】解:
由题意可知∠3=∠4=55°,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠2=∠3+∠4=110°,
∠1+∠2=180°,
∴∠1=70°,∠2=110°.
22.如图,MN和EF是两面互相平行的两个镜面.一束光线AB照射到镜面MN上,反射光线为BC,则有∠1=∠2.
(1)画出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
【解答】解:(1)如图,∠3=∠4,CD为所求;
(2)AB与CD的平行.理由如下:
∵∠1=∠2,
∴∠ABC=180°﹣2∠2,
∵光线BC经镜面EF反射后的反射光线CD,
∴∠3=∠4,
∴∠BCE=∠DCF,
∴∠BCD=180°﹣2∠BCE,
∵MN∥EF,
∴∠2=∠BCE,
∴∠ABC=∠BCD,
∴AB∥CD.
21世纪教育网(www.21cnjy.com)
人教新版七年级下册《5.3 平行线的性质》同步练习
一、选择题
1.如图,AB∥CD,∠1=50°,∠2的度数是( )
A.50° B.100° C.130° D.140°
2.如图所示,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
3.如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
A.110° B.115° C.120° D.125°
4.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=50°,那么∠2的度数是( )
A.20° B.30° C.40° D.50°
5.如图,直线a∥b,直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=55°,则∠2的度数是( )
A.50° B.70° C.80° D.110°
6.如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )
A.30° B.32° C.42° D.58°
7.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是( )
A.90° B.110° C.120° D.150°
8.如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是( )
A.30° B.40° C.50° D.60°
9.已知直线m∥n,将一块含30°角的直角三角板ABC按如图所示方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=25°,则∠2的度数为( )
A.25° B.30° C.45° D.55°
10.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B.60° C.80° D.120°
11.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数( )
A.10° B.25° C.30° D.35°
二、填空题
12.如图,若∠1=40°,∠2=40°,∠3=116°,则∠4= .
13.如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=48°,则∠2的度数为 .
14.如图,AB∥CD,BC∥DE,若角∠B=40°,则∠D的度数是 .
15.如图,AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则AE与CE的位置关系是 .
三、解答题
16.如图所示,已知AD∥BC,∠A=∠C,试说明AB∥CD.
思考1:由AD∥BC可得出哪些结论?
思考2:要证明AB∥CD,由哪些条件可证?
17.如图,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,求∠BPC的度数.
思考1:∠1和∠2是同位角吗?是内错角吗?是同旁内角吗?
思考2:由AB∥CD怎样构造图形,建立∠BPC和∠1与∠2的关系呢?
18.如图,水渠的两岸互相平行,修渠时要求拐弯处∠1=110°,那么∠2应等于多少度?为什么?
19.如图所示,已知AB∥CD,EF∥GC,你能否推出∠1=∠C?试说明理由.
20.如图,已知∠1=∠D=78°,∠2=62°,AE∥BC,求∠C的度数.
21.把一张长方形纸片ABCD沿EF折叠后,D,C分别在D′,C′的位置上,ED′与BC的交点为G,如图,若∠EFG=55°,求∠1与∠2的度数.
22.如图,MN和EF是两面互相平行的两个镜面.一束光线AB照射到镜面MN上,反射光线为BC,则有∠1=∠2.
(1)画出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
人教新版七年级下册《5.3 平行线的性质》2024年同步练习卷(5)
参考答案与试题解析
一、选择题
1.如图,AB∥CD,∠1=50°,∠2的度数是( )
A.50° B.100° C.130° D.140°
【解答】解:∵AB∥CD,
∴∠3=∠1=50°,
∴∠2=180°﹣∠3=130°.
故选:C.
2.如图所示,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
【解答】解:∵∠1+∠5=180°,∠1+∠2=180°,
∴∠2=∠5,
∴a∥b,
∴∠3=∠6=100°,
∴∠4=100°.
故选:D.
3.如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
A.110° B.115° C.120° D.125°
【解答】解:∵∠1=∠2,
∴l1∥l2,
∴∠4=∠2+∠3,
∵∠2=∠3=55°,
∴∠4=110°,
故选:A.
4.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=50°,那么∠2的度数是( )
A.20° B.30° C.40° D.50°
【解答】解:∵AB⊥BC,
∴∠ABC=90°,
∴∠3=180°﹣90°﹣∠1=40°,
∵a∥b,
∴∠2=∠3=40°.
故选:C.
5.如图,直线a∥b,直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=55°,则∠2的度数是( )
A.50° B.70° C.80° D.110°
【解答】解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵a∥b,∠1=55°,
∴∠BAD=∠CAD=55°,
∴∠2=180°﹣55°﹣55°=70°.
故选:B.
6.如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )
A.30° B.32° C.42° D.58°
【解答】解:如图,
过点A作AB∥b,
∴∠3=∠1=58°,
∵∠3+∠4=90°,
∴∠4=90°﹣∠3=32°,
∵a∥b,AB∥b,
∴AB∥a,
∴∠2=∠4=32°,
故选:B.
7.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是( )
A.90° B.110° C.120° D.150°
【解答】解:延长FE交DC于点N,
∵直线AB∥EF,
∴∠BCD=∠DNF=95°,
∵∠CDE=25°,
∴∠DEF=95°+25°=120°.
故选:C.
8.如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是( )
A.30° B.40° C.50° D.60°
【解答】解:∵AB∥EF,
∴∠A=∠2=50°,
∵AC∥DF,
∴∠1=∠A=50°.
故选:C.
9.已知直线m∥n,将一块含30°角的直角三角板ABC按如图所示方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=25°,则∠2的度数为( )
A.25° B.30° C.45° D.55°
【解答】解:∵∠ABC=30°,∠1=25°,
∴∠ABD=∠1+∠ABC=55°,
∵直线m∥n,
∴∠2=∠ABD=55°,
故选:D.
10.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B.60° C.80° D.120°
【解答】解:∵AD∥BC,∠B=30°,
∴∠EAD=∠B=30°,
∵AD是∠EAC的平分线,
∴∠EAC=2∠EAD=2×30°=60°,
∴∠C=∠EAC﹣∠B=60°﹣30°=30°.
故选:A.
11.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数( )
A.10° B.25° C.30° D.35°
【解答】解:如图,延长AB交CF于E,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵∠1=35°,
∴∠AEC=∠ABC﹣∠1=25°,
∵GH∥EF,
∴∠2=∠AEC=25°,
故选:B.
二、填空题
12.如图,若∠1=40°,∠2=40°,∠3=116°,则∠4= 64° .
【解答】解:∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴a∥b,
∴∠5=∠3=116°,
∴∠4=180°﹣∠3=64°
故答案为:64°.
13.如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=48°,则∠2的度数为 66° .
【解答】解:∵AB∥CD,
∴∠BEF+∠1=180°,∠BEG=∠2,
∵∠1=48°,
∴∠BEF=132°,
∵EG平分∠BEF,
∴∠BEG=66°,
∴∠2=66°,
故答案为:66°.
14.如图,AB∥CD,BC∥DE,若角∠B=40°,则∠D的度数是 140° .
【解答】解:∵AB∥CD,∠B=40°,
∴∠C=∠B=40°,
∵BC∥DE,
∴∠C+∠D=180°,
∴∠D=140°.
故答案为140°.
15.如图,AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则AE与CE的位置关系是 互相垂直 .
【解答】解:∵AB∥CD,
∴∠BAC+∠ACD=180°.
∵∠BAC的平分线和∠ACD的平分线交于点E,
∴∠EAC+∠ACE=(∠BAC+∠ACD)=90°,
∴∠AEC=180°﹣90°=90°,
∴AE与CE互相垂直.
故答案为:互相垂直.
三、解答题
16.如图所示,已知AD∥BC,∠A=∠C,试说明AB∥CD.
思考1:由AD∥BC可得出哪些结论?
思考2:要证明AB∥CD,由哪些条件可证?
【解答】解:思考1:由AD∥BC可得出∠A=∠ABF,∠A+∠ABC=180°,∠EDC=∠C,∠E=∠F,∠ADC+∠C=180°;
思考2:要证明AB∥CD,需证明∠ABF=∠C,∠A=∠CDE,∠A+∠ADC=180°,∠C+∠ABC=180°.
17.如图,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,求∠BPC的度数.
思考1:∠1和∠2是同位角吗?是内错角吗?是同旁内角吗?
思考2:由AB∥CD怎样构造图形,建立∠BPC和∠1与∠2的关系呢?
【解答】解:思考1:根据同位角、内错角、同旁内角的定义,∠1和∠2不是由两条直线被第三条直线所截形成的角,故∠1和∠2不是同位角,不是内错角,不是同旁内角;
思考2:过点P作PN∥AB,
∵AB∥CD,
∴PN∥CD,
∴∠1=∠3=32°,∠2=∠4=25°,
∴∠BPC=∠3+∠4=∠1+∠2=32°+25°=57°.
18.如图,水渠的两岸互相平行,修渠时要求拐弯处∠1=110°,那么∠2应等于多少度?为什么?
【解答】解:∠2=110°,理由如下:
如图,过点A、D作射线AH,
∵AB∥DM,AC∥DN,
∴∠BAH=∠MDH,∠CAH=∠NDH,
∴∠BAH+∠CAH=∠MDH+∠NDH,
即∠2=∠1,
∵∠1=110°,
∴∠2=110°.
19.如图所示,已知AB∥CD,EF∥GC,你能否推出∠1=∠C?试说明理由.
【解答】解:能推出∠1=∠C;
理由如下:∵AB∥CD,
∴∠C=∠CMB,
∵EF∥GC,
∴∠1=∠CMB,
∴∠1=∠C.
20.如图,已知∠1=∠D=78°,∠2=62°,AE∥BC,求∠C的度数.
【解答】解:∵∠1=∠D=78°,
∴AB∥CD,
∵∠2=62°,
∴∠3=∠2=62°,
∵AE∥BC,
∴∠C=∠3=62°
21.把一张长方形纸片ABCD沿EF折叠后,D,C分别在D′,C′的位置上,ED′与BC的交点为G,如图,若∠EFG=55°,求∠1与∠2的度数.
【解答】解:
由题意可知∠3=∠4=55°,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠2=∠3+∠4=110°,
∠1+∠2=180°,
∴∠1=70°,∠2=110°.
22.如图,MN和EF是两面互相平行的两个镜面.一束光线AB照射到镜面MN上,反射光线为BC,则有∠1=∠2.
(1)画出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
【解答】解:(1)如图,∠3=∠4,CD为所求;
(2)AB与CD的平行.理由如下:
∵∠1=∠2,
∴∠ABC=180°﹣2∠2,
∵光线BC经镜面EF反射后的反射光线CD,
∴∠3=∠4,
∴∠BCE=∠DCF,
∴∠BCD=180°﹣2∠BCE,
∵MN∥EF,
∴∠2=∠BCE,
∴∠ABC=∠BCD,
∴AB∥CD.
21世纪教育网(www.21cnjy.com)
