湖南省湘潭市高中新课程展示课:必修1—函数的单调性(湘锰中学 李会生)
文档属性
| 名称 | 湖南省湘潭市高中新课程展示课:必修1—函数的单调性(湘锰中学 李会生) |

|
|
| 格式 | rar | ||
| 文件大小 | 807.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-27 00:00:00 | ||
图片预览




文档简介
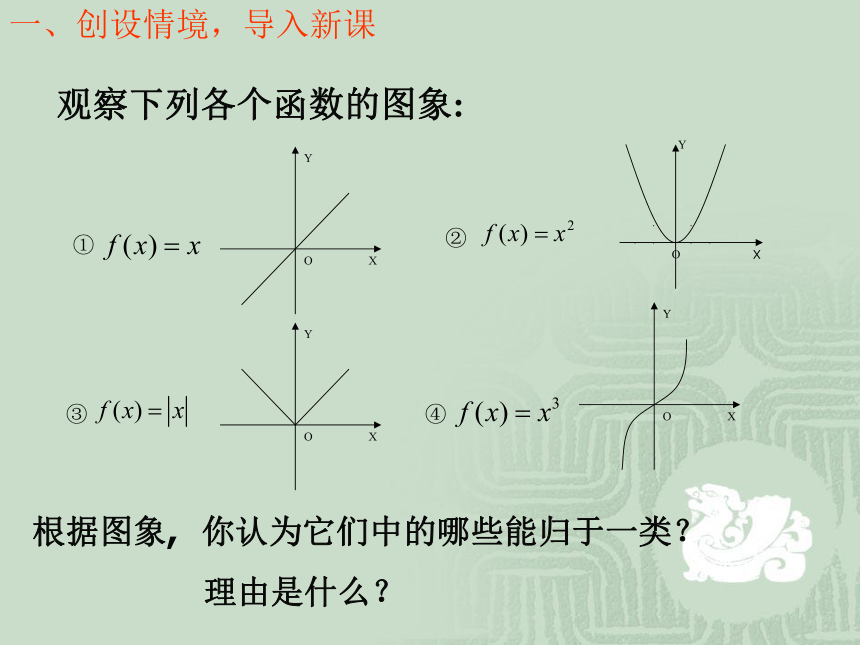
课件20张PPT。高中数学必修1 观察下列各个函数的图象:根据图象, 你认为它们中的哪些能归于一类?
理由是什么?一、创设情境,导入新课函数的单调性高中数学必修1
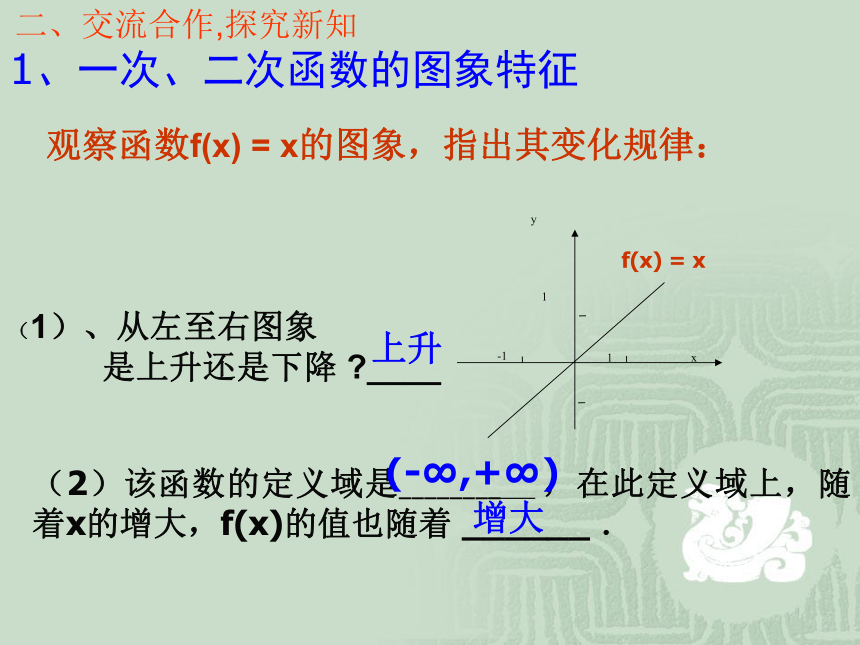
(2)该函数的定义域是________ ,在此定义域上,随着x的增大,f(x)的值也随着 ______ . (-∞,+∞)增大上升二、交流合作,探究新知1、一次、二次函数的图象特征(1)、从左至右图象
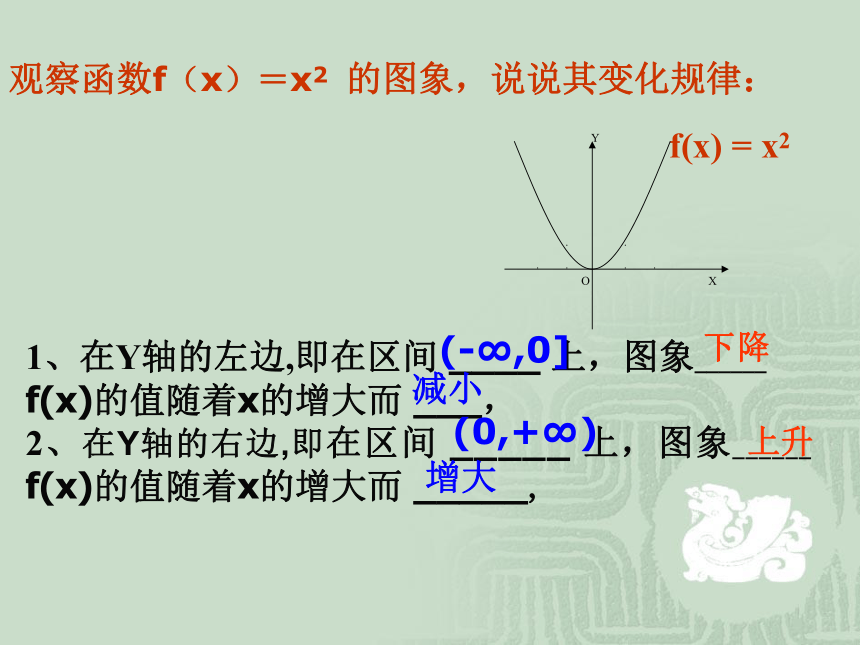
是上升还是下降 ?____ 1、在Y轴的左边,即在区间 ____ 上,图象______
f(x)的值随着x的增大而 ___,
2、在Y轴的右边,即在区间 _____ 上,图象______ f(x)的值随着x的增大而 _____, (-∞,0](0,+∞)增大减小下降上升综合上述两种情况,对于某种函数我们不能笼统地说
函数值y随着x的增大而增大,或函数值y随着x的增大而减小。这说明函数的这一增减特征是函数的 性质。 “局部”还是“整体” ?局部2、函数单调性定义的探究【问题】 .比较下列各组数的大小。
(1) 22, 32, 42
(2)(-4)2,(-3)2,(-2)2
【联想】对函数f(x) = x2
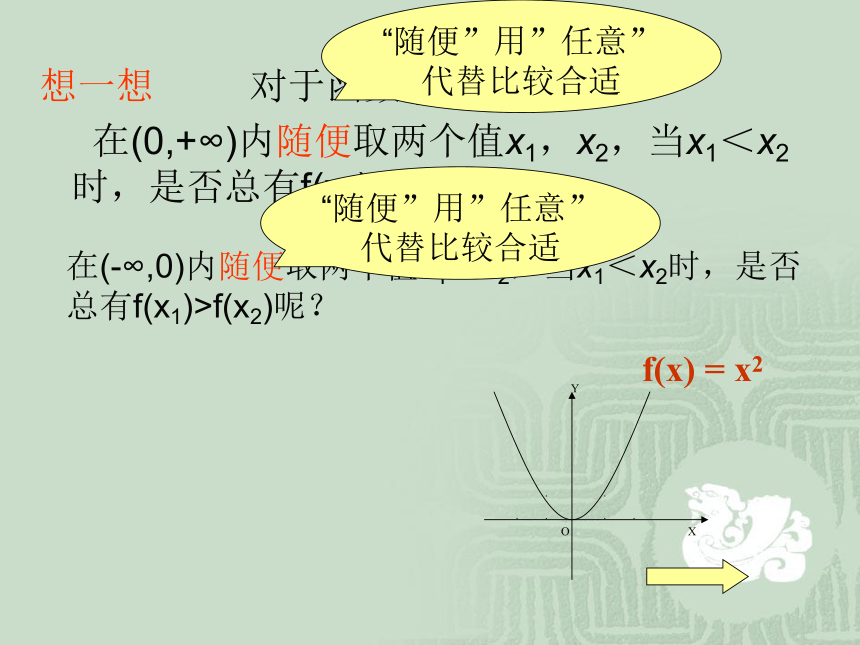
当0<x1<x2<x3时,有想一想 对于函数f(x) = x2:
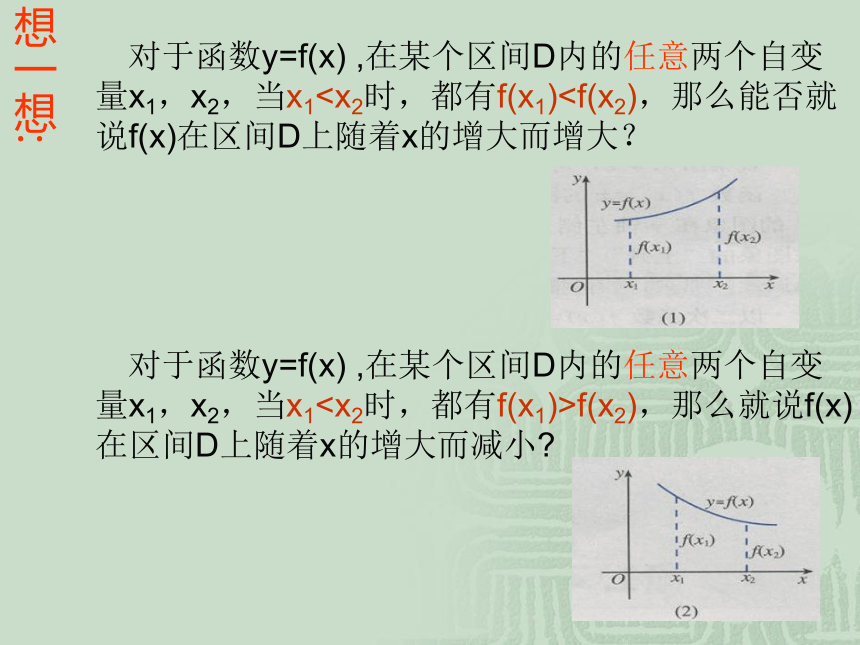
在(0,+∞)内随便取两个值x1,x2,当x1<x2时,是否总有f(x1) f(x) = x2在(-∞,0)内随便取两个值x1,x2,当x1<x2时,是否总有f(x1)>f(x2)呢? 对于函数y=f(x) ,在某个区间D内的任意两个自变量x1,x2,当x1 对于函数y=f(x) ,在某个区间D内的任意两个自变量x1,x2,当x1f(x2),那么就说f(x)在区间D上随着x的增大而减小?想一想:3、增函数、减函数的定义 那么就说f(x)在区间D上是增函数. 增函数一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量
量x1,x2,当x1f(x2),那么就说f(x)在区间D上是减函数 .减函数 如果函数y=f(x)在某个区间上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,
区间D叫做y=f(x)的单调区间. 4、.函数的单调性
1、函数的单调性是在定义域内的某个
区间上的性质,是函数的局部性质;注意! 2 、必须是对于区间D内的任意两个自变量 x1,x2;当x1f(x2) 才能称之在区间D内是增函数或减函数.例1、下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?解:函数y=f(x)的单调区间有 [-5,-2),[-2,1),[1,3),[3,5] 其中y=f(x)在区间[-5,-2), [1,3)是减函数,
在区间[-2,1), [3,5] 上是增函数。三、知识迁移,应用提高思考:能否写成
[-5,-2) ∪[1,3)?例2、证明:函数f(x)=1/x 在(0,+∞)上是减函数。证明:设x1,x2是(0,+∞)上任意两个实数,且x1变形结论1 任取x1,x2∈D,且x12 作差f(x1)-f(x2);
3 变形(通常是因式分解和配方);
4 定号(即判断差f(x1)-f(x2)的正负);
5 下结论(即指出函数f(x)在给定的区间D上的单调性). 利用定义判断或证明函数f(x)在给定的区间D上的单调性的一般步骤:证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V10, V2- V1 >0取值定号结论DCB当堂检测反馈:小结 取 值 → 作 差 → 变 形 → 定 号 → 下结论 四、总结提炼,拓展延伸1、增函数、减函数的定义 2、单调性、单调区间的概义3、单调性的证明拓展: 设f(x)是定义在R上的增函数,且f(xy)=f(x)+f(y),
(1)求f(0)、f(1)的值;
(2)若f(3)=1,求不等式f(x)+f(x-2)>1的解集.谢谢再见
理由是什么?一、创设情境,导入新课函数的单调性高中数学必修1
(2)该函数的定义域是________ ,在此定义域上,随着x的增大,f(x)的值也随着 ______ . (-∞,+∞)增大上升二、交流合作,探究新知1、一次、二次函数的图象特征(1)、从左至右图象
是上升还是下降 ?____ 1、在Y轴的左边,即在区间 ____ 上,图象______
f(x)的值随着x的增大而 ___,
2、在Y轴的右边,即在区间 _____ 上,图象______ f(x)的值随着x的增大而 _____, (-∞,0](0,+∞)增大减小下降上升综合上述两种情况,对于某种函数我们不能笼统地说
函数值y随着x的增大而增大,或函数值y随着x的增大而减小。这说明函数的这一增减特征是函数的 性质。 “局部”还是“整体” ?局部2、函数单调性定义的探究【问题】 .比较下列各组数的大小。
(1) 22, 32, 42
(2)(-4)2,(-3)2,(-2)2
【联想】对函数f(x) = x2
当0<x1<x2<x3时,有想一想 对于函数f(x) = x2:
在(0,+∞)内随便取两个值x1,x2,当x1<x2时,是否总有f(x1)
量x1,x2,当x1
区间D叫做y=f(x)的单调区间. 4、.函数的单调性
1、函数的单调性是在定义域内的某个
区间上的性质,是函数的局部性质;注意! 2 、必须是对于区间D内的任意两个自变量 x1,x2;当x1
在区间[-2,1), [3,5] 上是增函数。三、知识迁移,应用提高思考:能否写成
[-5,-2) ∪[1,3)?例2、证明:函数f(x)=1/x 在(0,+∞)上是减函数。证明:设x1,x2是(0,+∞)上任意两个实数,且x1
3 变形(通常是因式分解和配方);
4 定号(即判断差f(x1)-f(x2)的正负);
5 下结论(即指出函数f(x)在给定的区间D上的单调性). 利用定义判断或证明函数f(x)在给定的区间D上的单调性的一般步骤:证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1
(1)求f(0)、f(1)的值;
(2)若f(3)=1,求不等式f(x)+f(x-2)>1的解集.谢谢再见
