2008年市说课比赛之----图形的全等
文档属性
| 名称 | 2008年市说课比赛之----图形的全等 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-02 22:04:00 | ||
图片预览








文档简介
(共21张PPT)
一、教材分析
二、教法分析
四、教学分析
五、教学评价
说课流程
三、学法分析
<<图形的全等>>
翻折
平移
旋转
三角形的全等
图形的全等
(一) 教 学 内 容 的 地 位 和 作 用
一、教材分析
1、知识目标
3 、情感目标
2、技能目标
(二)教学目标
依据《新课标》要求,本阶段的学生应初步会运用数学的思维方式去观察、分析现实生活中的实际问题,体会数学与生活的联系。
培养学生观察能力,
应用能力。
培养学生的审美情趣,体会数学与生活的联系。
理解图形全等的概念,
掌握全等图形的特征,能识
别出全等的图形。
(三)教学重点、教学难点
依据《新课标》的有关要求,强调获得知识的过程远比知识本身更有价值,还强调要让学生经历知识的形成与应用过程,发展学生的应用意识和能力。结合学生的实际情
况我确定了:
教学重点:全等图形的相关概念,全等图形的特征,如何识别两个图形全等 。
教学难点:如何运用全等的知识解决实际问题。
二、教法分析
由于本节是在学习了图形变换后而
引入的, 因此知识切入点比较低,又初中
学生具有较强的好奇心,对新事物比较敏
感,就此我采用以“探究式”为主,讲授
法、启发式,多媒体辅助教学等多种
方法相结合。
三、学法分析
“探究式”和“有意义的接受式”是学生学习的重要方式。因此,本课我采用两者相结合。引导学生观察实验、自主探索,在合作交流中发现新知和发展能力,从而来体现“数学学习主要是数学活动的学习”的理念。
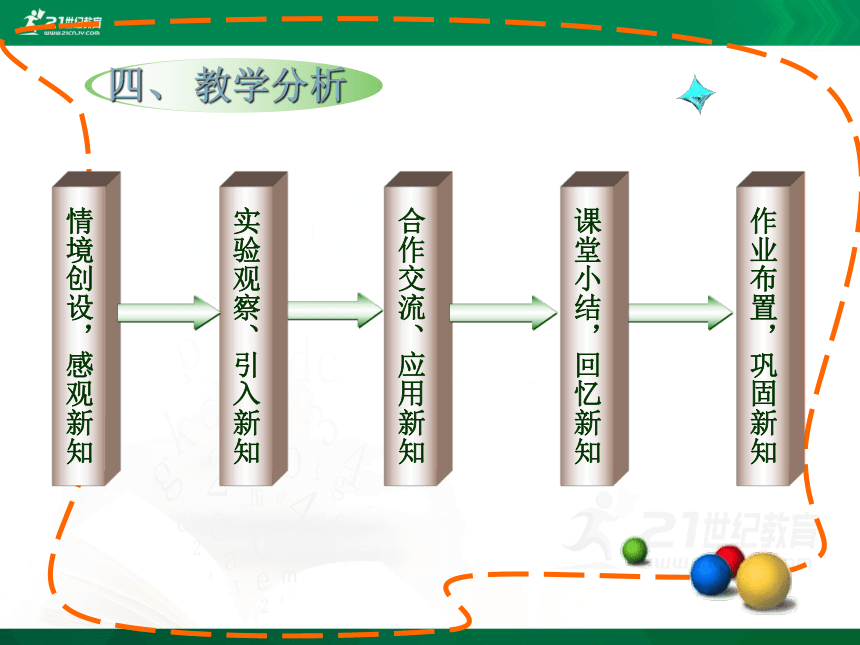
四、 教学分析
合作交流、应用新知
作业布置,巩固新知
情境创设,感观新知
实验观察、引入新知
课堂小结,回忆新知
活动一:下列同一类的图形经过变换后有什么特点?
特点:同一类图形经过平移、旋转、翻折运动后都能完全重合,说明同一类图形的形状、大小都相同。
(一)创设情景、感观新知
(1)
活动二:观察下面几何图形,从中找出能够完全重合的图形,与同学交流。
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(二)观察实验、引入新知
上图中(3)和(8)、(4)和(7)是否也是全等
图形?
(3)和(8), (4)和(7)两对图形都不能完全重合,因
此它们不是全等图形。
(3)
(4)
(7)
(8)
我们把能够完全重合的两个图形叫做
全等图形(congruent figures)。
活动三: 观察下图,两个四边形是全等图形,其中一个图形经过变换是否会和另一个图形重合?与同学交流一下。
左边两个多边形是全等图形,也称为全等多边形。两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角。
如图中的两个五边形是全等的,如何表示?
怎样找对应?
记作:五边形ABCDE ≌五边形A′B′C′D′E′(这
里,符号“≌”表示全等,读作“全等于”).点A与
A′、点B与B′、点C与C′、点D与D′、点E与E′分别
是对应顶点.
通过上面的演示,要求学生小组讨论并总结图形全等有何特征?
全等多边形
性质 全等多边形的对应边相等、 对应角相等
判定 边、 角分别对应相等的两个多边形全等
全等三角形
全等三角形的对应边相等、 对应角相等
边、角分别对应相等的两个三角形全等
活动四:分发纸片,让学生合作交流、动手操作。
1.沿图1中的虚线,把该图划分为两个全等图形.
2. 图2是一块等边三角形土地,为了绿化美观,你能
把它分成两个全等的三角形吗?分成三个、四个全等
的三角形吗?
图1
图2
(三)合作交流、实践应用
2.下图是一块等边三角形土地,为了绿化美观,你能把它分成两个全等的三角形吗?分成三个、四个全等的三角形吗?
(四)课堂小结,回忆新知:
(1)什么是图形的全等
(三角形) ?
(2)全等图形(三角形)
有何特征?
(3)如何识别两个图形
(三角形)全等?
(五)作业布置,巩固新知:
A组题(必做题)
1、(课本P87的习题)
2、在作业纸上画出两个全等的三角形,它们
可以拼凑出多少个不同四边形,画图说明。
B组题(选做题)
在作业纸上画出一个正方形,按下列要求作答:
(1)、你如何把它分解成两个全等的三角形,
画出图形说明;
(2)、你如何把它分解成四个全等的三角形,
画出图形说明;
(3)、你如何把它分解成两个全等的四边形,
画出图形说明;
B
A
C
D
五、教学评价
(一)重视知识的产生过程。本节课的教学是借助多媒体辅助教学,以生活图片激发学生的学习兴趣,通过实验观察、交流合作,让学生脑、嘴、手并动,从而得出全等图形的概念、特征,并学会自己分割图形,由此积累他们对全等图形的体验。体现了“数学教学主要是数学活动的教学” 的教育理念。
(二)关注人性的发展。考虑到学生的个性,对于课堂的素材和课外练习的选取,我忠实于教材,但不迷信于教材。对于教学环节的设计和课外作业的安排上,我都注意到个体间的差异,注意分层教学,“关注人性的发展,让不同的人在数学上能得到不同的发展”,体现了课改的理念。
谢谢指导!
一、教材分析
二、教法分析
四、教学分析
五、教学评价
说课流程
三、学法分析
<<图形的全等>>
翻折
平移
旋转
三角形的全等
图形的全等
(一) 教 学 内 容 的 地 位 和 作 用
一、教材分析
1、知识目标
3 、情感目标
2、技能目标
(二)教学目标
依据《新课标》要求,本阶段的学生应初步会运用数学的思维方式去观察、分析现实生活中的实际问题,体会数学与生活的联系。
培养学生观察能力,
应用能力。
培养学生的审美情趣,体会数学与生活的联系。
理解图形全等的概念,
掌握全等图形的特征,能识
别出全等的图形。
(三)教学重点、教学难点
依据《新课标》的有关要求,强调获得知识的过程远比知识本身更有价值,还强调要让学生经历知识的形成与应用过程,发展学生的应用意识和能力。结合学生的实际情
况我确定了:
教学重点:全等图形的相关概念,全等图形的特征,如何识别两个图形全等 。
教学难点:如何运用全等的知识解决实际问题。
二、教法分析
由于本节是在学习了图形变换后而
引入的, 因此知识切入点比较低,又初中
学生具有较强的好奇心,对新事物比较敏
感,就此我采用以“探究式”为主,讲授
法、启发式,多媒体辅助教学等多种
方法相结合。
三、学法分析
“探究式”和“有意义的接受式”是学生学习的重要方式。因此,本课我采用两者相结合。引导学生观察实验、自主探索,在合作交流中发现新知和发展能力,从而来体现“数学学习主要是数学活动的学习”的理念。
四、 教学分析
合作交流、应用新知
作业布置,巩固新知
情境创设,感观新知
实验观察、引入新知
课堂小结,回忆新知
活动一:下列同一类的图形经过变换后有什么特点?
特点:同一类图形经过平移、旋转、翻折运动后都能完全重合,说明同一类图形的形状、大小都相同。
(一)创设情景、感观新知
(1)
活动二:观察下面几何图形,从中找出能够完全重合的图形,与同学交流。
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(二)观察实验、引入新知
上图中(3)和(8)、(4)和(7)是否也是全等
图形?
(3)和(8), (4)和(7)两对图形都不能完全重合,因
此它们不是全等图形。
(3)
(4)
(7)
(8)
我们把能够完全重合的两个图形叫做
全等图形(congruent figures)。
活动三: 观察下图,两个四边形是全等图形,其中一个图形经过变换是否会和另一个图形重合?与同学交流一下。
左边两个多边形是全等图形,也称为全等多边形。两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角。
如图中的两个五边形是全等的,如何表示?
怎样找对应?
记作:五边形ABCDE ≌五边形A′B′C′D′E′(这
里,符号“≌”表示全等,读作“全等于”).点A与
A′、点B与B′、点C与C′、点D与D′、点E与E′分别
是对应顶点.
通过上面的演示,要求学生小组讨论并总结图形全等有何特征?
全等多边形
性质 全等多边形的对应边相等、 对应角相等
判定 边、 角分别对应相等的两个多边形全等
全等三角形
全等三角形的对应边相等、 对应角相等
边、角分别对应相等的两个三角形全等
活动四:分发纸片,让学生合作交流、动手操作。
1.沿图1中的虚线,把该图划分为两个全等图形.
2. 图2是一块等边三角形土地,为了绿化美观,你能
把它分成两个全等的三角形吗?分成三个、四个全等
的三角形吗?
图1
图2
(三)合作交流、实践应用
2.下图是一块等边三角形土地,为了绿化美观,你能把它分成两个全等的三角形吗?分成三个、四个全等的三角形吗?
(四)课堂小结,回忆新知:
(1)什么是图形的全等
(三角形) ?
(2)全等图形(三角形)
有何特征?
(3)如何识别两个图形
(三角形)全等?
(五)作业布置,巩固新知:
A组题(必做题)
1、(课本P87的习题)
2、在作业纸上画出两个全等的三角形,它们
可以拼凑出多少个不同四边形,画图说明。
B组题(选做题)
在作业纸上画出一个正方形,按下列要求作答:
(1)、你如何把它分解成两个全等的三角形,
画出图形说明;
(2)、你如何把它分解成四个全等的三角形,
画出图形说明;
(3)、你如何把它分解成两个全等的四边形,
画出图形说明;
B
A
C
D
五、教学评价
(一)重视知识的产生过程。本节课的教学是借助多媒体辅助教学,以生活图片激发学生的学习兴趣,通过实验观察、交流合作,让学生脑、嘴、手并动,从而得出全等图形的概念、特征,并学会自己分割图形,由此积累他们对全等图形的体验。体现了“数学教学主要是数学活动的教学” 的教育理念。
(二)关注人性的发展。考虑到学生的个性,对于课堂的素材和课外练习的选取,我忠实于教材,但不迷信于教材。对于教学环节的设计和课外作业的安排上,我都注意到个体间的差异,注意分层教学,“关注人性的发展,让不同的人在数学上能得到不同的发展”,体现了课改的理念。
谢谢指导!
