2008年市说课比赛之----有理数的乘方
文档属性
| 名称 | 2008年市说课比赛之----有理数的乘方 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-01 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
有理数的乘方(说课)
一、教材分析
二、教学方法
三、教学过程设计
四、教学设计说明与教后反思
1、知识技能目标:在现实背景中,理解有理数乘方的意义,掌握有理数的乘方运算。
2、过程与方法目标:培养学生观察、分析、比较、归纳、概括的能力,渗透转化思想。
3、情感态度价值观目标:培养学生勤思,认真,勇于探索的精神,并联系实际,加强理解,体会数学给我们的生活带来的便利。.
2、难点:对有理数乘方的意义的深入理解
并能运用乘方解决实际问题。
有理数的乘方是初一年级上学期第二章第十一节的教学内容,是有理数的一种基本运算。是在学生学习了有理数的加、减、乘、除运算的基础上来学习的,它既是有理数乘法的推广和延续,又是后继学习有理数的混合运算、科学记数法和开方的基础,起到承前启后、铺路架桥的作用。在这一课的教学过程中,可以培养学生观察问题、分析问题和解决问题的能力,以及转化的数学思想,通过这一课的学习,对培养学生的这些能力和转化的数学思想,渗透国情教育等起到很重要的作用。
一、教 材 分 析
1.地位和作用
2.教学目标
3.教材的重点和难点
1、重点:正确理解乘方的意义,掌握乘方
运算法则,能进行有理数的乘方运算。
一、教材分析
二、教学方法
三、教学过程设计
四、教学设计说明与教后反思
1. 教学方法
二、教学方法
启发诱导式、实践探究式。教学过程中渗透类比的数学思想,形成新的知识结构体系;设置探究式教学,让学生经历知识的形成,从而达到对知识的深刻理解与灵活应用 。
3.教学手段
根据初一学生好动、好问、好奇的心理特征,课堂上采取由浅入深的启发诱导,随着教学内容的深入,让学生一步一步的跟着动脑、动手、动口,在合作交流中培养学生学习的积极性和主动性,使学习方式由“学会”变为“会学”。
2. 学法引导
利用多媒体教学,目的之一是使课堂生动、形象又直观,能激发学生的学习兴趣,目的之二是增大教学容量,增强教学效果。
一、教材分析
二、教学方法
三、教学过程设计
四、教学设计说明与教后反思
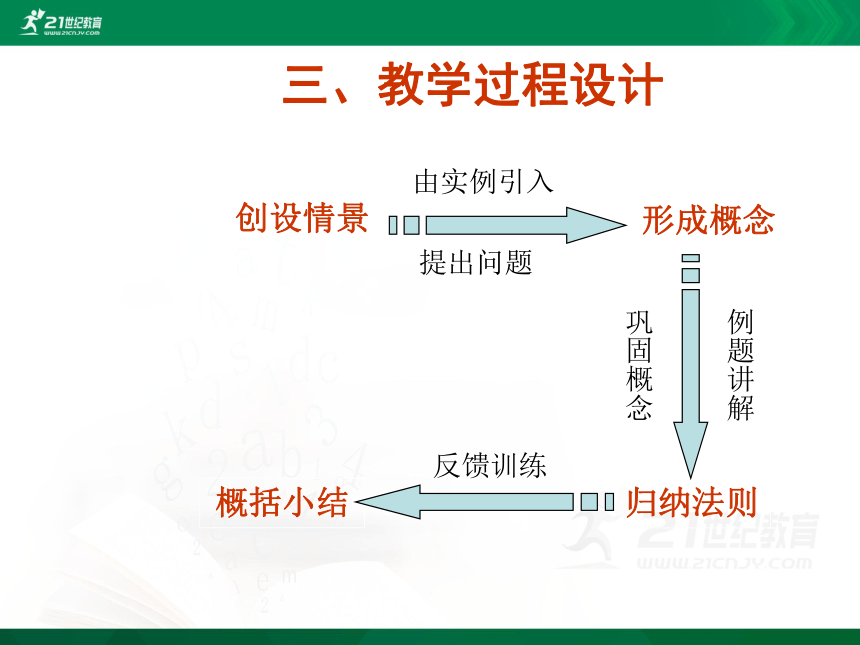
创设情景
形成概念
归纳法则
概括小结
三、教学过程设计
由实例引入
巩固概念
例题讲解
反馈训练
提出问题
大家知道2008年北京的奥运圣火将上珠穆朗玛峰,每一个中国人都将引以为豪,那么众所周珠穆朗玛峰是世界的最高峰,它的海拔高度是8848.43米
你相信吗?
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度可以超过珠穆朗玛峰。你相信吗?
(5)对折二十次有几层?
探究过程要求:把一张纸进行对折、再对折……并作记录(同桌合作:操作者,记录者)
动手
问题:(1)对折一次有几层?
(2)对折二次有几层?
(3)对折三次有几层?
(4)对折四次有几层?
…… ……
(6)对折三十次呢?
…… ……
20个
(1)对折一次有几层?
2
(3)对折三次有几层?
2×2
(2)对折二次有几层?
(4)对折四次有几层?
(5)对折二十次有几层?
2×2 ×2
2×2 ×2 ×2
2×2 ×2 …… 2×2 ×2
它能不能用一个简单的式子表示呢 那么这样的式子读作什么呢?
(6)对折三十次有几层?
…… ……
2×2 ×2 …… 2×2 ×2
30个
2×2
2×2×2
2×2×2×2
……
2×2×2×……×2
20个2
=22
=24
=220
=23
2个
3个
4个
30个
n个
2×2×2×……×2
30个2
=230
an
乘方的结果叫做幂。
读做“ 的 次方”,或读做“ 的 次幂”。
幂
指数
(因数的个数)
底数
(相同因数)
这种求几个相同因数的积的运算叫做乘方,
a×a ×… ×a ×a
n个a
记做
an
请同学们读一下:(1)(-7 ) 、(2)(-2 )
3
2
(1 ) 读作: -7的2次方或-7的2次幂
通常读作:
(2 ) 读作: -2的3次方或-2的3次幂
通常读作:
-7的平方
-2的立方
底数是:__;指数是:__.
-7
2
其中-2叫做_____;3叫做_____;
底数
指数
7
7
7
底数
指数
-3
10
-3
-3
10
(3) 5的底数是____,指数是_____。
5
1
一个数可以看做这个数本身的一次方,1通常省略不写
例
计算
温馨提示
发现什么,得出什么结论
100
1000
10000
100000
100
-1000
10000
-100000
0.01
0.001
0.0001
0.00001
0.01
-0.001
0.0001
-0.00001
想一想:观察上述计算结果,你发现了什么规律?
(1)10的几次方,1后面就有几个0。
(2)0.1的几次方,1前面就有几个0。
(3)正数的任何次幂,还是正数。
(4)负数的奇数次幂是负数,偶数次幂是正数。
(三)探索法则
看谁算得又对又快。
(四)课堂练习
课本63页练习 1.2.
课堂练习
看谁算得又快又准
(1)如果底数是带分数,应如何进行乘方运算?
(2) 与 的意义是否相同?运算结果是否相等? 与 呢?
(3)在计算 时, 前面的负号能不能与括号内的负号相乘?
(4) 与 一样吗? 与 呢?
1048576×0.1=104857.6(毫米)
104.8576 ÷ 3≈ 35(层)
连续对折20次,纸片变为1048576层,若对折的纸厚度为0.1毫米,会有多厚?它相当于大概多少层楼高?(若每层楼为3米)
解:
104857.6毫米=104.8576米
若连续对折30次,它有多厚呢 ×0.1=1073741824(毫米)
1073741824毫米=107374.1824米
107374÷8848≈12(层)
12个珠穆朗玛峰高
通过这节课的学习,你有什么收获?你还有什么疑惑?
强调重难点
1.有理数的乘方的意义和相关概念。幂的底数是分数或负数时,底数应该添上括号.
2.乘方的有关运算。
3.体会特殊到一般,具体到抽象的数学方法。
★(六)布置课外作业.
选做题.4. 补充:
(五) 归纳小结
★课本63页习题2.11 必做题 1.2.3.
5.截止到1999年底,我国人口约13亿,如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少。(结果精确到亿位;可用计算器)
一、教材分析
二、教学方法
三、教学过程设计
四、教学设计说明与教后反思
教学设计说明
2.教学方法与设置:
教学开始,结合国际热点提出问题,借助多媒体手段,引发学生积极思考,并归结出答案,由答案的表现形式再给学生提出问题,激发学生的求知欲望,在教师的启发诱导下自然过度到新的学习,接着层层设问,引出乘方以及与乘方有关的概念。
在探索法则的教学环节中,用比一比的形式来激发学生的学习兴趣,教师放手学生操作把课堂还给学生,真正体现学生的主体地位,教师起到一个合作者、组织者、引导者的作用,学生在合作交流与自主探索的过程中归纳出有理数乘方的符号法则。
教学设计说明
3.教学反馈与评价:
为了使学生真正掌握重难点,熟练的进行有理数的乘方运算,设计了能力训练环节,在生生互动、师生互动的教学过程中,教学难点得以突破,学生的能力得到提高,同时培养了学生集体合作的意识。
整节课中,学生全面参与,全员参与,全程参与,充分发挥了学生在学习过程中自觉性,活动性和创造性,寓教育于教学之中。
板 书 设 计
有理数的乘方
一、有理数的乘方概念 例:…………
二、结论 练习栏...
(1)10的几次方,1后面就有几个0。
(2)0.1的几次方,1前面就有几个0。
(3)正数的任何次幂,还是正数。
(4)负数的奇数次幂是负数,偶数次幂是正数。
谢 谢
再 见
有理数的乘方(说课)
一、教材分析
二、教学方法
三、教学过程设计
四、教学设计说明与教后反思
1、知识技能目标:在现实背景中,理解有理数乘方的意义,掌握有理数的乘方运算。
2、过程与方法目标:培养学生观察、分析、比较、归纳、概括的能力,渗透转化思想。
3、情感态度价值观目标:培养学生勤思,认真,勇于探索的精神,并联系实际,加强理解,体会数学给我们的生活带来的便利。.
2、难点:对有理数乘方的意义的深入理解
并能运用乘方解决实际问题。
有理数的乘方是初一年级上学期第二章第十一节的教学内容,是有理数的一种基本运算。是在学生学习了有理数的加、减、乘、除运算的基础上来学习的,它既是有理数乘法的推广和延续,又是后继学习有理数的混合运算、科学记数法和开方的基础,起到承前启后、铺路架桥的作用。在这一课的教学过程中,可以培养学生观察问题、分析问题和解决问题的能力,以及转化的数学思想,通过这一课的学习,对培养学生的这些能力和转化的数学思想,渗透国情教育等起到很重要的作用。
一、教 材 分 析
1.地位和作用
2.教学目标
3.教材的重点和难点
1、重点:正确理解乘方的意义,掌握乘方
运算法则,能进行有理数的乘方运算。
一、教材分析
二、教学方法
三、教学过程设计
四、教学设计说明与教后反思
1. 教学方法
二、教学方法
启发诱导式、实践探究式。教学过程中渗透类比的数学思想,形成新的知识结构体系;设置探究式教学,让学生经历知识的形成,从而达到对知识的深刻理解与灵活应用 。
3.教学手段
根据初一学生好动、好问、好奇的心理特征,课堂上采取由浅入深的启发诱导,随着教学内容的深入,让学生一步一步的跟着动脑、动手、动口,在合作交流中培养学生学习的积极性和主动性,使学习方式由“学会”变为“会学”。
2. 学法引导
利用多媒体教学,目的之一是使课堂生动、形象又直观,能激发学生的学习兴趣,目的之二是增大教学容量,增强教学效果。
一、教材分析
二、教学方法
三、教学过程设计
四、教学设计说明与教后反思
创设情景
形成概念
归纳法则
概括小结
三、教学过程设计
由实例引入
巩固概念
例题讲解
反馈训练
提出问题
大家知道2008年北京的奥运圣火将上珠穆朗玛峰,每一个中国人都将引以为豪,那么众所周珠穆朗玛峰是世界的最高峰,它的海拔高度是8848.43米
你相信吗?
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度可以超过珠穆朗玛峰。你相信吗?
(5)对折二十次有几层?
探究过程要求:把一张纸进行对折、再对折……并作记录(同桌合作:操作者,记录者)
动手
问题:(1)对折一次有几层?
(2)对折二次有几层?
(3)对折三次有几层?
(4)对折四次有几层?
…… ……
(6)对折三十次呢?
…… ……
20个
(1)对折一次有几层?
2
(3)对折三次有几层?
2×2
(2)对折二次有几层?
(4)对折四次有几层?
(5)对折二十次有几层?
2×2 ×2
2×2 ×2 ×2
2×2 ×2 …… 2×2 ×2
它能不能用一个简单的式子表示呢 那么这样的式子读作什么呢?
(6)对折三十次有几层?
…… ……
2×2 ×2 …… 2×2 ×2
30个
2×2
2×2×2
2×2×2×2
……
2×2×2×……×2
20个2
=22
=24
=220
=23
2个
3个
4个
30个
n个
2×2×2×……×2
30个2
=230
an
乘方的结果叫做幂。
读做“ 的 次方”,或读做“ 的 次幂”。
幂
指数
(因数的个数)
底数
(相同因数)
这种求几个相同因数的积的运算叫做乘方,
a×a ×… ×a ×a
n个a
记做
an
请同学们读一下:(1)(-7 ) 、(2)(-2 )
3
2
(1 ) 读作: -7的2次方或-7的2次幂
通常读作:
(2 ) 读作: -2的3次方或-2的3次幂
通常读作:
-7的平方
-2的立方
底数是:__;指数是:__.
-7
2
其中-2叫做_____;3叫做_____;
底数
指数
7
7
7
底数
指数
-3
10
-3
-3
10
(3) 5的底数是____,指数是_____。
5
1
一个数可以看做这个数本身的一次方,1通常省略不写
例
计算
温馨提示
发现什么,得出什么结论
100
1000
10000
100000
100
-1000
10000
-100000
0.01
0.001
0.0001
0.00001
0.01
-0.001
0.0001
-0.00001
想一想:观察上述计算结果,你发现了什么规律?
(1)10的几次方,1后面就有几个0。
(2)0.1的几次方,1前面就有几个0。
(3)正数的任何次幂,还是正数。
(4)负数的奇数次幂是负数,偶数次幂是正数。
(三)探索法则
看谁算得又对又快。
(四)课堂练习
课本63页练习 1.2.
课堂练习
看谁算得又快又准
(1)如果底数是带分数,应如何进行乘方运算?
(2) 与 的意义是否相同?运算结果是否相等? 与 呢?
(3)在计算 时, 前面的负号能不能与括号内的负号相乘?
(4) 与 一样吗? 与 呢?
1048576×0.1=104857.6(毫米)
104.8576 ÷ 3≈ 35(层)
连续对折20次,纸片变为1048576层,若对折的纸厚度为0.1毫米,会有多厚?它相当于大概多少层楼高?(若每层楼为3米)
解:
104857.6毫米=104.8576米
若连续对折30次,它有多厚呢 ×0.1=1073741824(毫米)
1073741824毫米=107374.1824米
107374÷8848≈12(层)
12个珠穆朗玛峰高
通过这节课的学习,你有什么收获?你还有什么疑惑?
强调重难点
1.有理数的乘方的意义和相关概念。幂的底数是分数或负数时,底数应该添上括号.
2.乘方的有关运算。
3.体会特殊到一般,具体到抽象的数学方法。
★(六)布置课外作业.
选做题.4. 补充:
(五) 归纳小结
★课本63页习题2.11 必做题 1.2.3.
5.截止到1999年底,我国人口约13亿,如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少。(结果精确到亿位;可用计算器)
一、教材分析
二、教学方法
三、教学过程设计
四、教学设计说明与教后反思
教学设计说明
2.教学方法与设置:
教学开始,结合国际热点提出问题,借助多媒体手段,引发学生积极思考,并归结出答案,由答案的表现形式再给学生提出问题,激发学生的求知欲望,在教师的启发诱导下自然过度到新的学习,接着层层设问,引出乘方以及与乘方有关的概念。
在探索法则的教学环节中,用比一比的形式来激发学生的学习兴趣,教师放手学生操作把课堂还给学生,真正体现学生的主体地位,教师起到一个合作者、组织者、引导者的作用,学生在合作交流与自主探索的过程中归纳出有理数乘方的符号法则。
教学设计说明
3.教学反馈与评价:
为了使学生真正掌握重难点,熟练的进行有理数的乘方运算,设计了能力训练环节,在生生互动、师生互动的教学过程中,教学难点得以突破,学生的能力得到提高,同时培养了学生集体合作的意识。
整节课中,学生全面参与,全员参与,全程参与,充分发挥了学生在学习过程中自觉性,活动性和创造性,寓教育于教学之中。
板 书 设 计
有理数的乘方
一、有理数的乘方概念 例:…………
二、结论 练习栏...
(1)10的几次方,1后面就有几个0。
(2)0.1的几次方,1前面就有几个0。
(3)正数的任何次幂,还是正数。
(4)负数的奇数次幂是负数,偶数次幂是正数。
谢 谢
再 见
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
