人教版数学六年级下册寒假预习-4.3.2 图形的放大与缩小(含解析)
文档属性
| 名称 | 人教版数学六年级下册寒假预习-4.3.2 图形的放大与缩小(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 187.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-22 20:05:29 | ||
图片预览



文档简介
寒假预习-4.3.2 图形的放大与缩小
人教版数学 六年级下册
一、填空题
1.人们喜欢的照相就是把物体( )的现象。照相所得图像与原图比较,( )变化了,( )没变。
2.一个正方形的边长为,如果把它按缩小,那么边长变为( );如果把它按放大,那么边长变为( )。
3.一个正方形边长5cm,按4∶1扩大后的正方形的周长是( )厘米,面积是( )平方厘米。
4.一个长方形长9cm,宽6cm,按1∶3缩小后的长方形周长是( )cm,面积是( )cm2。
5.根据图形A按2∶1放大后得到的图形是( )。
6.两位同学分别对同一个零件按照20∶1和25∶1的比例尺放大,结果图纸上两个零件的长度差6.5厘米,那么这个零件的实际长度是( )厘米。
7.如图,两个三角形均为等边三角形,并且小三角形的边长是大三角形边长的一半,那么小三角形的面积与中间空白部分面积的比是( )。
8.把一个长方形缩小到原来的,它的周长缩小到原来的( ),面积缩小到原来的( )。
二、判断题
9.一个长5m、宽3m的长方形按2∶1放大后,得到图形的面积是60m2。( )
10.一个40°的角在5倍的放大镜下观察,角度是200°。( )
11.把一个图形按1∶3缩小后,图形各边的长度都缩小到原来的。( )
12.一个正方形的边长是100cm,把它按1∶10缩小。缩小后的面积是1dm2。( )
13.把一个长方形按3∶1进行放大,就是把长方形的长扩大到原来的3倍,宽不变。( )
三、选择题
14.把一个边长2cm的正方形按4∶1放大后,面积是( )cm2。
A.8 B.32 C.64
15.把一个长4厘米,宽2厘米的长方形按4∶1放大,所得到的图形的面积是( )平方厘米。
A.32 B.72 C.128
16.将一个周长12厘米的正方形变换成面积为36平方厘米的正方形,是按( )的比放大的.
A.2:1 B.3:1 C.4:1
17.一个三角形的三个内角的度数比是2∶3∶4,把这个三角形按1∶2的比例缩小后,最大的角是( )。
A.40° B.80° C.160°
18.将一个图形按1∶3缩小,缩小后的图形的( )变为原来的。
A.内角的度数 B.面积 C.周长
四、作图题
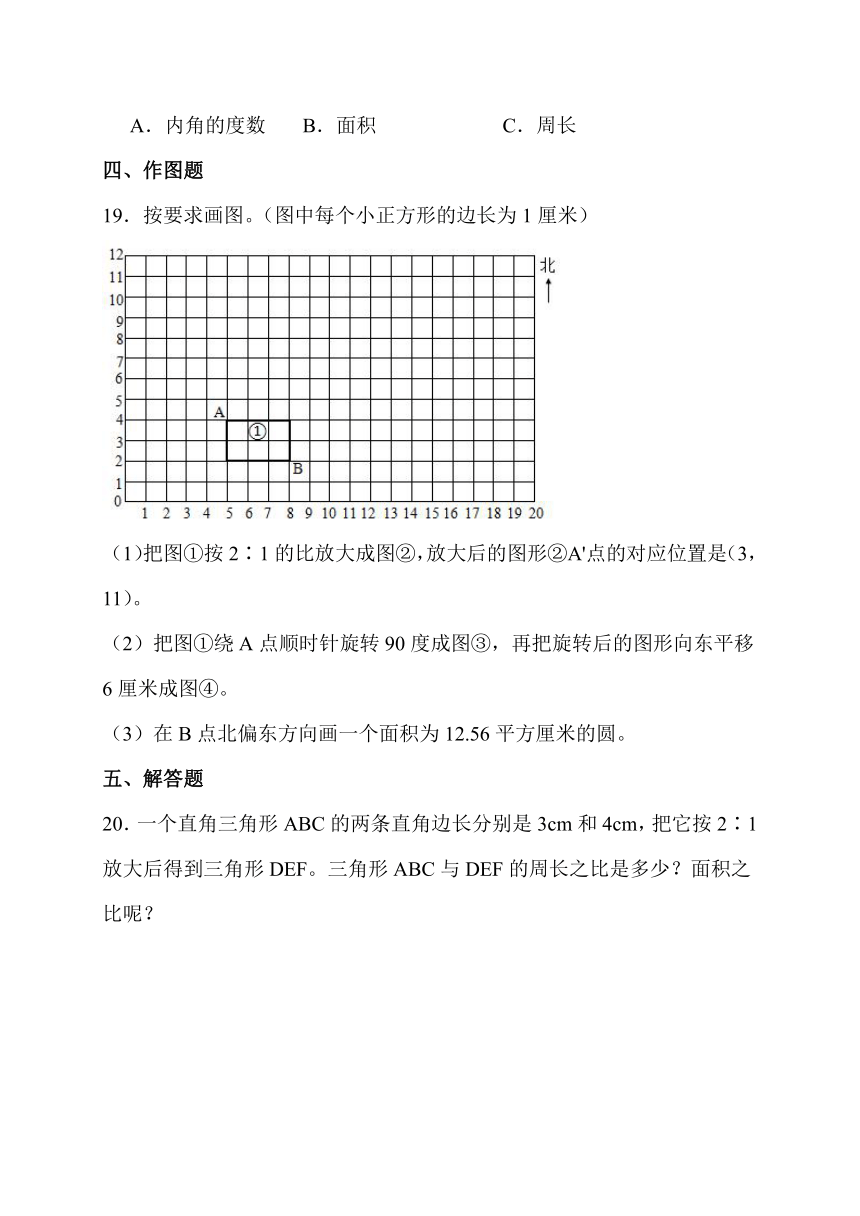
19.按要求画图。(图中每个小正方形的边长为1厘米)
(1)把图①按2∶1的比放大成图②,放大后的图形②A'点的对应位置是(3,11)。
(2)把图①绕A点顺时针旋转90度成图③,再把旋转后的图形向东平移6厘米成图④。
(3)在B点北偏东方向画一个面积为12.56平方厘米的圆。
五、解答题
20.一个直角三角形ABC的两条直角边长分别是3cm和4cm,把它按2∶1放大后得到三角形DEF。三角形ABC与DEF的周长之比是多少?面积之比呢?
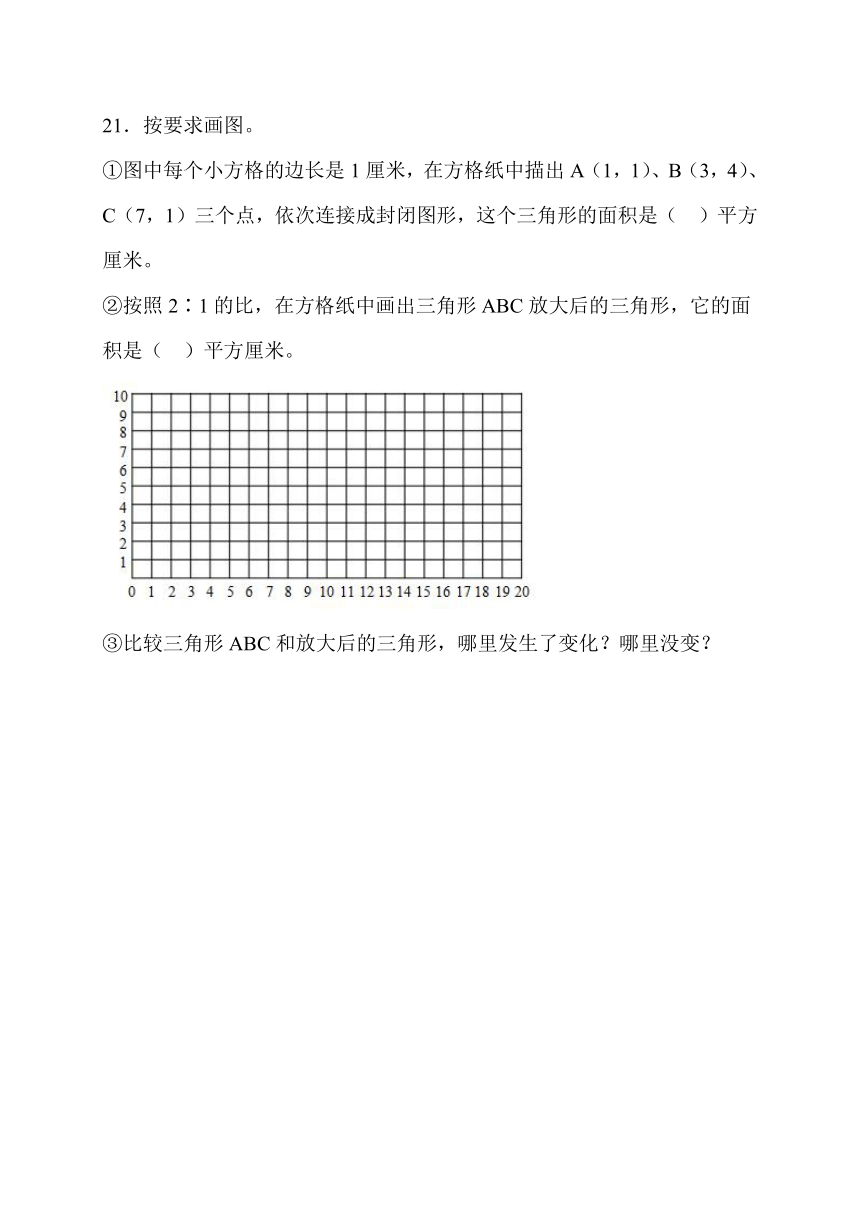
21.按要求画图。
①图中每个小方格的边长是1厘米,在方格纸中描出A(1,1)、B(3,4)、C(7,1)三个点,依次连接成封闭图形,这个三角形的面积是( )平方厘米。
②按照2∶1的比,在方格纸中画出三角形ABC放大后的三角形,它的面积是( )平方厘米。
③比较三角形ABC和放大后的三角形,哪里发生了变化?哪里没变?
参考答案:
1. 放大或缩小 大小 形状
【详解】根据实际生活经验及图形方法或缩小的相关知识可知:人们喜欢的照相就是把物体放大或缩小的现象。照相所得图像与原图比较,大小变化了,形状没变。
2.
【分析】一个正方形的边长为,如果把它按缩小,即把这个正方形的边长缩小到原来的,根据分数乘法的意义,。如果把它按放大,即边长放大到原来的5倍,根据整数乘法的意义,。
【详解】
即一个正方形的边长为,如果把它按缩小,那么边长变为;如果把它按放大,那么边长变为。
【点睛】一个图形放大或缩小的倍数是指对应边放大或缩小的倍数(对应角大小不变)。用比表示一个图形放大或缩小的倍数时,前项表示放大或缩小后图形的边长,后项表示原图形对应边的长度。
3. 80 400
【分析】正方形按4∶1扩大后,边长变为20厘米,再根据正方形的周长和面积公式计算即可。
【详解】按4∶1扩大后,正方形的边长为5×4=20(厘米);
周长:20×4=80(厘米);
面积:20×20=400(平方厘米)
【点睛】明确按一定的比例扩大后,正方形的边长是多少是解答本题的关键。
4. 10 6
【分析】1∶3=,长9m,宽6cm的长方形按1∶3的比缩小,即长和宽缩小到原来的,用乘法计算得缩小后的图形的长和宽,再利用长方形的周长公式和长方形的面积公式,求出缩小后的图形周长和面积。据此解答。
【详解】9×=3(cm)
6×=2(cm)
(3+2)×2
=5×2
=10(cm)
3×2=6(cm2)
即按1∶3缩小后的长方形周长是10cm,面积是6cm2。
【点睛】本题是考查图形的放大与缩小以及长方形周长、面积的计算。
5.③
【分析】把一个图形按照2∶1放大,就是把这个图形的各条边长按照2∶1进行放大,一般只要确定这个图形的长与高的长度比即可。观察图形,先找出另外三个图形的长与高的长度,再求出它们与原图形对对应边的比,即可判断选择。
【详解】由分析可知:
根据图形A按2∶1放大后得到的图形是③。
【点睛】本题主要考查图形的放大与缩小的意义:注意放大或缩小后的图形的边长:原图的对应边长=放大或缩小的比。
6.1.3
【分析】根据题意,同一个零件按照20∶1和25∶1的比例尺放大,即前一个放大到实际长度的20倍,后一个放大到实际长度的25倍,那么后一个比前一个多放大了实际长度的(25-20)倍,用图纸上两个零件的长度差除以多放大的倍数,即可求出这个零件的实际长度。
【详解】6.5÷(25-20)
=6.5÷5
=1.3(厘米)
这个零件的实际长度是1.3厘米。
【点睛】本题考查图形的放大比例尺的意义及应用,找出长度差6.5厘米对应的倍数差是解题的关键。
7.1∶3
【分析】大等边三角形的边长是小等边三角形的2倍,那么大等边三角形的面积是小等边三角形的4倍,那么空白部分面积是小三角形的面积的3倍。
【详解】大三角形与小三角形的边长比,2∶1;
大三角形与小三角形的面积比,4∶1;
4-1=3
所以小三角形的面积与中间空白部分面积比,1∶3。
【点睛】当图形按比例进行放缩时,边长扩大n倍,面积扩大n2倍。
8.
【分析】“把一个长方形缩小到原来的”是把长方形的长和宽分别缩小到原来的。如果原来长方形的长用a表示,宽用b表示,那么现在长方形的长为a,宽为b。再根据长方形周长和面积公式,把原来长方形的周长和面积、现在长方形的周长和面积分别用含有a,b的式子表示。最后比较现在长方形的周长与原来长方形的周长的关系,现在长方形的面积与原来长方形的面积的关系。
【详解】原来长方形的周长:2(a+b)
现在长方形的周长:2(a+b)=2×(a+b)=×2(a+b)
所以它的周长缩小到原来的。
原来长方形的面积:ab
现在长方形的面积:a×b=ab
所以它的面积缩小到原来的。
【点睛】把一个图形按指定的比放大或缩小,它的周长就按指定的比扩大或缩小,它的面积就按指定比的平方扩大或缩小。
9.√
【分析】将长方形按2∶1放大,则放大后的长和宽都是原来的2倍,用长方形的长和宽分别乘2求出放大后的长和宽,用放大后的长乘宽即可求出得到图形的面积。
【详解】5×2=10(m)
3×2=6(m)
10×6=60(m2)
故答案为:√
【点睛】明确按2∶1放大后,得到的图形的长和宽分别为多少是解答本题的关键。
10.×
【分析】从一点引出两条射线所形成的图形叫做角。角的大小与两边的长短无关,只与两边叉开的大小有关。用放大镜看角,只是角的边长增长,两边叉开的角度并没有变化,据此判断。
【详解】一个40°的角在5倍的放大镜下观察,角度仍是40°。原题说法错误。
故答案为:×
【点睛】掌握角的大小与两边的关系,以及放大镜放大角的特点是解题的关键。
11.√
【分析】依据比例尺的意义,即“图上距离与实际距离的比即为比例尺”,一个图形按1∶3缩小,就是把这个图形的边长按照1∶3缩小,缩小后的图形与原图形相比大小变了,形状没变。
【详解】把一个图形按1∶3缩小后,图形各边的长度都缩小到原来的。原题说法正确。
故答案:√。
【点睛】此题考查图形放大与缩小的方法。
12.√
【分析】先求出正方形按1∶10缩小后的边长;再根据“正方形的面积=边长×边长”求出缩小后的正方形的面积。
【详解】100×=10(cm)
10×10=100(cm2)
100cm2=1dm2
所以缩小后的面积是1dm2。原题说法正确。
故答案为:√
【点睛】把一个平面图形按一定的比放大或缩小,它的面积就按这个比的平方扩大或缩小。
13.×
【分析】图形的放大或缩小是指围成图形的每条线段按比例放大或缩小。图形放大与缩小的特点:形状相同,大小不同;据此判断。
【详解】根据图形放大与缩小的意义可知,把长方形按3∶1进行放大,就是把长方形的长和宽分别扩大到原来的3倍。
原题说法错误。
故答案为:×
【点睛】掌握图形放大与缩小的特点是解题的关键,明确放大或缩小图形,只改变图形的大小,不改变图形的形状。
14.C
【分析】把一个边长是2cm的正方形按4∶1放大后,也就是把这个正方形的边长扩大到原来的4倍,即边长乘4,我们知道正方形面积是边长×边长,即可求出放大后的正方形的面积。
【详解】(2×4)×(2×4)
=8×8
=64(cm2)
故答案为:C
【点睛】本题的解题关键是掌握图形放大与缩小后面积的计算方法。
15.C
【分析】长方形按4∶1放大,则这个长方形的长和宽都放大4倍,据此先求出放大后的长方形的长和宽,再利用长方形的面积公式求出它的面积即可。
【详解】4×4×(2×4)
=16×8
=128(平方厘米)
故答案为:C
【点睛】本题考查了图形的放大,图形按一定的比例放大,图形的每条边都放大相应的倍数。
16.A
【分析】求出原来正方形的边长与扩大后正方形的边长,按新图形:原图形计算.
【详解】原边长:12÷4=3(厘米),新边长是6厘米,6:3=2:1.
17.B
【分析】一个三角形的三个内角度数的比是2∶3∶4,把这个三角形按1∶2的比例缩小后,最大角的度数不变,依据三角形的内角和定理,利用按比例分配的方法,即可求出最大角的度数。
【详解】180°÷(2+3+4)×4
=180°÷9×4
=20°×4
=80°
所以最大的角是80°。
故答案为:B
【点睛】解答本题关键是明确:把一个图形放大或缩小后所得到的图形与原图形相比,形状相同,大小不同。
18.C
【分析】图形的放大或缩小是指围成图形的每条线段按比例放大或缩小。图形的放大与缩小的特点:形状相同,大小不同;据此解答。
【详解】根据图形缩小的特点,将一个图形按1∶3缩小,图形的形状不变,所以缩小后图形的内角的度数不变,缩小后的图形的边长、周长变为原来的,面积变为原来的。
故答案为:C
【点睛】本题考查图形放大或缩小的意义及特点,明确图形放大或缩小后对应边、对应角以及对应周长、面积的变化规律。
19.
【分析】(1)把图①的长和宽扩大到原来的2倍是图②,再按照放大后的图形②A'点的对应位置是(3,11),找到图形②的位置;
(2)把图①连接点A的长和宽绕A点顺时针旋转90度,找到旋转后的顶点,再连接画出图③,再把图③的各个顶点向东平移6厘米,连接各顶点,画出图④;
(3)先根据圆的面积公式求出圆的半径,再画出圆即可。(答案不唯一)
【详解】(1)如图所示:
(2)如图所示:
(3)12.56(厘米)
(厘米)
画出的圆如图所示:
【点睛】本题考查平移、旋转、图形的放大与缩小,解答本题的关键是掌握平移、旋转、图形的放大与缩小的概念。
20.2∶1;4∶1
【分析】根据图形放大或缩小的特征可知:放大后的三角形周长之比为边长之比,面积之比为边长之比的平方的比,据此解答。
【详解】把三角形ABC按2∶1放大后得到三角形DEF。
周长之比是2∶1;面积之比是22∶12=4∶1。
答:三角形ABC与DEF的周长之比是2∶1,面积之比是4∶1。
【点睛】根据图形放大或缩小的特征,熟练掌握放大或缩小后的图形周长之比、面积之比与边长之比的关系是解决本题的关键。
21.①见详解;9
②见详解;36
③见详解
【分析】①用数对表示位置,数对的第一个数表示列,第二个数表示行;在方格纸中描出A(1,1)、B(3,4)、C(7,1)三个点,依次连接成封闭图形;再根据三角形的面积=底×高÷2,求出这个三角形的面积。
②把三角形ABC的各边按2∶1的比放大,再根据三角形的面积公式求出放大后的三角形的面积。
③图形的放大与缩小的特点:形状相同,大小不同;据此解答。
【详解】①三角形ABC的底是6厘米,高是3厘米;
三角形ABC的面积是:
6×3÷2
=18÷2
=9(平方厘米)
②放大后的三角形的底是:6×2=12(厘米)
放大后的三角形的高是:3×2=6(厘米)
放大后三角形的面积是:
12×6÷2
=72÷2
=36(平方厘米)
如图:
③比较三角形ABC和放大后的三角形,大小发生了变化,形状没变。
【点睛】掌握根据数对找位置、三角形的面积的计算、作放大后的图形以及图形放大的特点是解题的关键。
人教版数学 六年级下册
一、填空题
1.人们喜欢的照相就是把物体( )的现象。照相所得图像与原图比较,( )变化了,( )没变。
2.一个正方形的边长为,如果把它按缩小,那么边长变为( );如果把它按放大,那么边长变为( )。
3.一个正方形边长5cm,按4∶1扩大后的正方形的周长是( )厘米,面积是( )平方厘米。
4.一个长方形长9cm,宽6cm,按1∶3缩小后的长方形周长是( )cm,面积是( )cm2。
5.根据图形A按2∶1放大后得到的图形是( )。
6.两位同学分别对同一个零件按照20∶1和25∶1的比例尺放大,结果图纸上两个零件的长度差6.5厘米,那么这个零件的实际长度是( )厘米。
7.如图,两个三角形均为等边三角形,并且小三角形的边长是大三角形边长的一半,那么小三角形的面积与中间空白部分面积的比是( )。
8.把一个长方形缩小到原来的,它的周长缩小到原来的( ),面积缩小到原来的( )。
二、判断题
9.一个长5m、宽3m的长方形按2∶1放大后,得到图形的面积是60m2。( )
10.一个40°的角在5倍的放大镜下观察,角度是200°。( )
11.把一个图形按1∶3缩小后,图形各边的长度都缩小到原来的。( )
12.一个正方形的边长是100cm,把它按1∶10缩小。缩小后的面积是1dm2。( )
13.把一个长方形按3∶1进行放大,就是把长方形的长扩大到原来的3倍,宽不变。( )
三、选择题
14.把一个边长2cm的正方形按4∶1放大后,面积是( )cm2。
A.8 B.32 C.64
15.把一个长4厘米,宽2厘米的长方形按4∶1放大,所得到的图形的面积是( )平方厘米。
A.32 B.72 C.128
16.将一个周长12厘米的正方形变换成面积为36平方厘米的正方形,是按( )的比放大的.
A.2:1 B.3:1 C.4:1
17.一个三角形的三个内角的度数比是2∶3∶4,把这个三角形按1∶2的比例缩小后,最大的角是( )。
A.40° B.80° C.160°
18.将一个图形按1∶3缩小,缩小后的图形的( )变为原来的。
A.内角的度数 B.面积 C.周长
四、作图题
19.按要求画图。(图中每个小正方形的边长为1厘米)
(1)把图①按2∶1的比放大成图②,放大后的图形②A'点的对应位置是(3,11)。
(2)把图①绕A点顺时针旋转90度成图③,再把旋转后的图形向东平移6厘米成图④。
(3)在B点北偏东方向画一个面积为12.56平方厘米的圆。
五、解答题
20.一个直角三角形ABC的两条直角边长分别是3cm和4cm,把它按2∶1放大后得到三角形DEF。三角形ABC与DEF的周长之比是多少?面积之比呢?
21.按要求画图。
①图中每个小方格的边长是1厘米,在方格纸中描出A(1,1)、B(3,4)、C(7,1)三个点,依次连接成封闭图形,这个三角形的面积是( )平方厘米。
②按照2∶1的比,在方格纸中画出三角形ABC放大后的三角形,它的面积是( )平方厘米。
③比较三角形ABC和放大后的三角形,哪里发生了变化?哪里没变?
参考答案:
1. 放大或缩小 大小 形状
【详解】根据实际生活经验及图形方法或缩小的相关知识可知:人们喜欢的照相就是把物体放大或缩小的现象。照相所得图像与原图比较,大小变化了,形状没变。
2.
【分析】一个正方形的边长为,如果把它按缩小,即把这个正方形的边长缩小到原来的,根据分数乘法的意义,。如果把它按放大,即边长放大到原来的5倍,根据整数乘法的意义,。
【详解】
即一个正方形的边长为,如果把它按缩小,那么边长变为;如果把它按放大,那么边长变为。
【点睛】一个图形放大或缩小的倍数是指对应边放大或缩小的倍数(对应角大小不变)。用比表示一个图形放大或缩小的倍数时,前项表示放大或缩小后图形的边长,后项表示原图形对应边的长度。
3. 80 400
【分析】正方形按4∶1扩大后,边长变为20厘米,再根据正方形的周长和面积公式计算即可。
【详解】按4∶1扩大后,正方形的边长为5×4=20(厘米);
周长:20×4=80(厘米);
面积:20×20=400(平方厘米)
【点睛】明确按一定的比例扩大后,正方形的边长是多少是解答本题的关键。
4. 10 6
【分析】1∶3=,长9m,宽6cm的长方形按1∶3的比缩小,即长和宽缩小到原来的,用乘法计算得缩小后的图形的长和宽,再利用长方形的周长公式和长方形的面积公式,求出缩小后的图形周长和面积。据此解答。
【详解】9×=3(cm)
6×=2(cm)
(3+2)×2
=5×2
=10(cm)
3×2=6(cm2)
即按1∶3缩小后的长方形周长是10cm,面积是6cm2。
【点睛】本题是考查图形的放大与缩小以及长方形周长、面积的计算。
5.③
【分析】把一个图形按照2∶1放大,就是把这个图形的各条边长按照2∶1进行放大,一般只要确定这个图形的长与高的长度比即可。观察图形,先找出另外三个图形的长与高的长度,再求出它们与原图形对对应边的比,即可判断选择。
【详解】由分析可知:
根据图形A按2∶1放大后得到的图形是③。
【点睛】本题主要考查图形的放大与缩小的意义:注意放大或缩小后的图形的边长:原图的对应边长=放大或缩小的比。
6.1.3
【分析】根据题意,同一个零件按照20∶1和25∶1的比例尺放大,即前一个放大到实际长度的20倍,后一个放大到实际长度的25倍,那么后一个比前一个多放大了实际长度的(25-20)倍,用图纸上两个零件的长度差除以多放大的倍数,即可求出这个零件的实际长度。
【详解】6.5÷(25-20)
=6.5÷5
=1.3(厘米)
这个零件的实际长度是1.3厘米。
【点睛】本题考查图形的放大比例尺的意义及应用,找出长度差6.5厘米对应的倍数差是解题的关键。
7.1∶3
【分析】大等边三角形的边长是小等边三角形的2倍,那么大等边三角形的面积是小等边三角形的4倍,那么空白部分面积是小三角形的面积的3倍。
【详解】大三角形与小三角形的边长比,2∶1;
大三角形与小三角形的面积比,4∶1;
4-1=3
所以小三角形的面积与中间空白部分面积比,1∶3。
【点睛】当图形按比例进行放缩时,边长扩大n倍,面积扩大n2倍。
8.
【分析】“把一个长方形缩小到原来的”是把长方形的长和宽分别缩小到原来的。如果原来长方形的长用a表示,宽用b表示,那么现在长方形的长为a,宽为b。再根据长方形周长和面积公式,把原来长方形的周长和面积、现在长方形的周长和面积分别用含有a,b的式子表示。最后比较现在长方形的周长与原来长方形的周长的关系,现在长方形的面积与原来长方形的面积的关系。
【详解】原来长方形的周长:2(a+b)
现在长方形的周长:2(a+b)=2×(a+b)=×2(a+b)
所以它的周长缩小到原来的。
原来长方形的面积:ab
现在长方形的面积:a×b=ab
所以它的面积缩小到原来的。
【点睛】把一个图形按指定的比放大或缩小,它的周长就按指定的比扩大或缩小,它的面积就按指定比的平方扩大或缩小。
9.√
【分析】将长方形按2∶1放大,则放大后的长和宽都是原来的2倍,用长方形的长和宽分别乘2求出放大后的长和宽,用放大后的长乘宽即可求出得到图形的面积。
【详解】5×2=10(m)
3×2=6(m)
10×6=60(m2)
故答案为:√
【点睛】明确按2∶1放大后,得到的图形的长和宽分别为多少是解答本题的关键。
10.×
【分析】从一点引出两条射线所形成的图形叫做角。角的大小与两边的长短无关,只与两边叉开的大小有关。用放大镜看角,只是角的边长增长,两边叉开的角度并没有变化,据此判断。
【详解】一个40°的角在5倍的放大镜下观察,角度仍是40°。原题说法错误。
故答案为:×
【点睛】掌握角的大小与两边的关系,以及放大镜放大角的特点是解题的关键。
11.√
【分析】依据比例尺的意义,即“图上距离与实际距离的比即为比例尺”,一个图形按1∶3缩小,就是把这个图形的边长按照1∶3缩小,缩小后的图形与原图形相比大小变了,形状没变。
【详解】把一个图形按1∶3缩小后,图形各边的长度都缩小到原来的。原题说法正确。
故答案:√。
【点睛】此题考查图形放大与缩小的方法。
12.√
【分析】先求出正方形按1∶10缩小后的边长;再根据“正方形的面积=边长×边长”求出缩小后的正方形的面积。
【详解】100×=10(cm)
10×10=100(cm2)
100cm2=1dm2
所以缩小后的面积是1dm2。原题说法正确。
故答案为:√
【点睛】把一个平面图形按一定的比放大或缩小,它的面积就按这个比的平方扩大或缩小。
13.×
【分析】图形的放大或缩小是指围成图形的每条线段按比例放大或缩小。图形放大与缩小的特点:形状相同,大小不同;据此判断。
【详解】根据图形放大与缩小的意义可知,把长方形按3∶1进行放大,就是把长方形的长和宽分别扩大到原来的3倍。
原题说法错误。
故答案为:×
【点睛】掌握图形放大与缩小的特点是解题的关键,明确放大或缩小图形,只改变图形的大小,不改变图形的形状。
14.C
【分析】把一个边长是2cm的正方形按4∶1放大后,也就是把这个正方形的边长扩大到原来的4倍,即边长乘4,我们知道正方形面积是边长×边长,即可求出放大后的正方形的面积。
【详解】(2×4)×(2×4)
=8×8
=64(cm2)
故答案为:C
【点睛】本题的解题关键是掌握图形放大与缩小后面积的计算方法。
15.C
【分析】长方形按4∶1放大,则这个长方形的长和宽都放大4倍,据此先求出放大后的长方形的长和宽,再利用长方形的面积公式求出它的面积即可。
【详解】4×4×(2×4)
=16×8
=128(平方厘米)
故答案为:C
【点睛】本题考查了图形的放大,图形按一定的比例放大,图形的每条边都放大相应的倍数。
16.A
【分析】求出原来正方形的边长与扩大后正方形的边长,按新图形:原图形计算.
【详解】原边长:12÷4=3(厘米),新边长是6厘米,6:3=2:1.
17.B
【分析】一个三角形的三个内角度数的比是2∶3∶4,把这个三角形按1∶2的比例缩小后,最大角的度数不变,依据三角形的内角和定理,利用按比例分配的方法,即可求出最大角的度数。
【详解】180°÷(2+3+4)×4
=180°÷9×4
=20°×4
=80°
所以最大的角是80°。
故答案为:B
【点睛】解答本题关键是明确:把一个图形放大或缩小后所得到的图形与原图形相比,形状相同,大小不同。
18.C
【分析】图形的放大或缩小是指围成图形的每条线段按比例放大或缩小。图形的放大与缩小的特点:形状相同,大小不同;据此解答。
【详解】根据图形缩小的特点,将一个图形按1∶3缩小,图形的形状不变,所以缩小后图形的内角的度数不变,缩小后的图形的边长、周长变为原来的,面积变为原来的。
故答案为:C
【点睛】本题考查图形放大或缩小的意义及特点,明确图形放大或缩小后对应边、对应角以及对应周长、面积的变化规律。
19.
【分析】(1)把图①的长和宽扩大到原来的2倍是图②,再按照放大后的图形②A'点的对应位置是(3,11),找到图形②的位置;
(2)把图①连接点A的长和宽绕A点顺时针旋转90度,找到旋转后的顶点,再连接画出图③,再把图③的各个顶点向东平移6厘米,连接各顶点,画出图④;
(3)先根据圆的面积公式求出圆的半径,再画出圆即可。(答案不唯一)
【详解】(1)如图所示:
(2)如图所示:
(3)12.56(厘米)
(厘米)
画出的圆如图所示:
【点睛】本题考查平移、旋转、图形的放大与缩小,解答本题的关键是掌握平移、旋转、图形的放大与缩小的概念。
20.2∶1;4∶1
【分析】根据图形放大或缩小的特征可知:放大后的三角形周长之比为边长之比,面积之比为边长之比的平方的比,据此解答。
【详解】把三角形ABC按2∶1放大后得到三角形DEF。
周长之比是2∶1;面积之比是22∶12=4∶1。
答:三角形ABC与DEF的周长之比是2∶1,面积之比是4∶1。
【点睛】根据图形放大或缩小的特征,熟练掌握放大或缩小后的图形周长之比、面积之比与边长之比的关系是解决本题的关键。
21.①见详解;9
②见详解;36
③见详解
【分析】①用数对表示位置,数对的第一个数表示列,第二个数表示行;在方格纸中描出A(1,1)、B(3,4)、C(7,1)三个点,依次连接成封闭图形;再根据三角形的面积=底×高÷2,求出这个三角形的面积。
②把三角形ABC的各边按2∶1的比放大,再根据三角形的面积公式求出放大后的三角形的面积。
③图形的放大与缩小的特点:形状相同,大小不同;据此解答。
【详解】①三角形ABC的底是6厘米,高是3厘米;
三角形ABC的面积是:
6×3÷2
=18÷2
=9(平方厘米)
②放大后的三角形的底是:6×2=12(厘米)
放大后的三角形的高是:3×2=6(厘米)
放大后三角形的面积是:
12×6÷2
=72÷2
=36(平方厘米)
如图:
③比较三角形ABC和放大后的三角形,大小发生了变化,形状没变。
【点睛】掌握根据数对找位置、三角形的面积的计算、作放大后的图形以及图形放大的特点是解题的关键。
