椭圆的几何性质(广东省江门市)

课件19张PPT。椭圆的简单几何性质1.解析几何要解决的两类基本问题是什么?
答:(1)已知曲线研究其方程;
(2)已知曲线方程研究其曲线的性质.
2.在高一学习函数性质后,研究了一些具体函数,你能列举几种吗?对于一个新函数,你认为应从哪些方面着手研究?
y=ax(a>0,a≠1),y=logax(a>0,a≠1),y=sinx等;研究一个新函数一般应从定义域、值域、奇偶性、单调性及某些特殊点，如与x轴、y轴的交点，图象最高点、最低点等方面入手。复习：3. 椭圆的标准方程是什么？椭圆的简单几何性质—研究问题1、顶点：
A1(-a,0),A2(a,0),B1(0,-b),B2(0,b)
因此椭圆与它的对称轴共有四个交点，
即：A1，A2，B1，B2。这四个点叫做椭圆的顶点。
线段A1A2叫椭圆的长轴，其长度等于2a;线段B1B2叫椭圆的短轴，其长度等于2b;线段C1C2叫椭圆的焦距，其长度等于2c.
在直角三角形F2OB2中│OB2│＝b，│OF2│＝c， │F2B2│＝a。显然有 a2 = b2 + c2方程：2、范围：
从图象上看：-a≤x≤a, -b≤y≤b
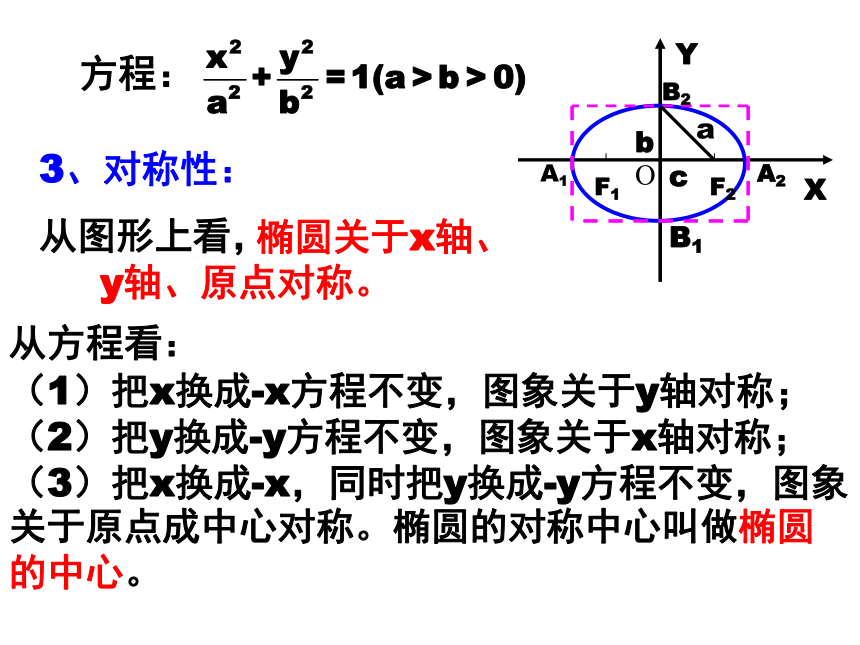
从方程看：方程：故椭圆位于 y =±b, x = ±a所围成的矩形内。3、对称性：
从图形上看，
椭圆关于x轴、
y轴、原点对称。从方程看：
（1）把x换成-x方程不变，图象关于y轴对称；
（2）把y换成-y方程不变，图象关于x轴对称；
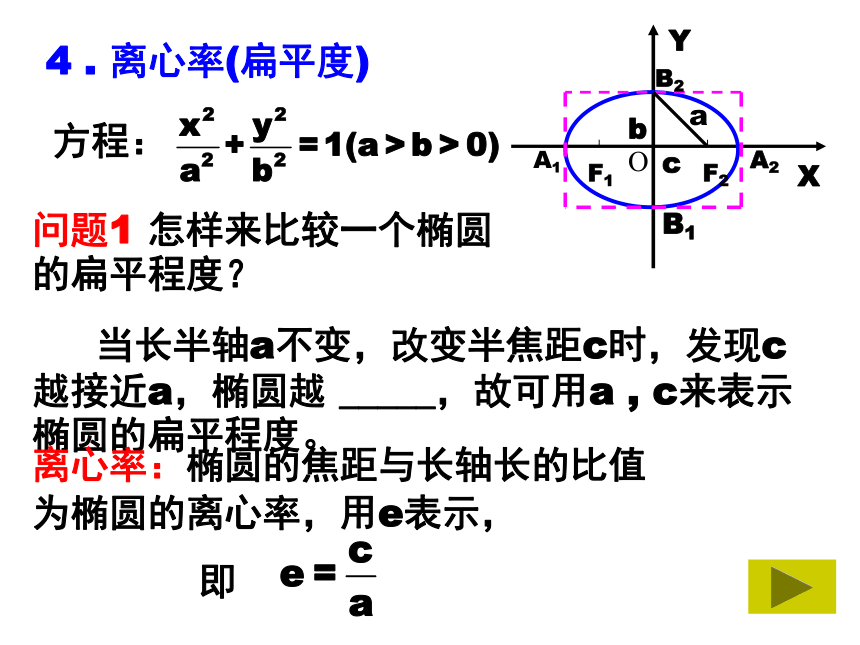
（3）把x换成-x，同时把y换成-y方程不变，图象关于原点成中心对称。椭圆的对称中心叫做椭圆的中心。方程：4 . 离心率(扁平度)方程：问题1 怎样来比较一个椭圆的扁平程度？ 当长半轴a不变，改变半焦距c时，发现c越接近a，椭圆越 _____，故可用a , c来表示椭圆的扁平程度。离心率：椭圆的焦距与长轴长的比值为椭圆的离心率，用e表示，
即因为a>c>0，所以0 故 当e=0时为圆 , 当0 当e=1时为线段思考：
1. 椭圆的离心率在什么范围内？
.当椭圆的离心率从0到1时椭圆的变化是怎
么样的？
.当e＝0时，曲线是什么？当e＝1时曲线又
是什么？椭圆的简单几何性质—研究问题xyo-a≤x≤a, -b≤y≤b-a≤y≤a, -b≤x≤b(-a,0), (a,0), (0,-b), (0,b)(-b,0), (b,0), (0,-a), (0,a)x轴、y轴、原点对称x轴、y轴、原点对称0例2：我国自行研制的“中星20号”通讯卫星，于2003年11月15日升空精确地进入预定轨道。这颗卫星运行轨道，是以地球的中心为一个焦点的椭圆，近地点与地球表面距离是439km，远地点与地球表面地距离是2384km。已知地球半径为6371km。求这颗卫星运行轨道地近似方程（长、短半轴长精确到0.1km）
例2：我国自行研制的“中星20号”通讯卫星，于2003年11月15日升空精确地进入预定轨道。这颗卫星运行轨道，是以地球的中心为一个焦点的椭圆，近地点与地球表面距离是439km，远地点与地球表面地距离是2384km。已知地球半径为6371km。求这颗卫星运行轨道地近似方程（长、短半轴长精确到1km）F2F10AB解：如图,建立直角坐标系，使点A、B、F2在x轴上,F2为椭圆的右焦点(记F1为左焦点). 因为椭圆的焦点在x轴上,所以设它的标准方程为F2则 a-c=|OA|-|OF2|=|F2A|
=6371+439=6810,
a+c=|OB|+|OF2|=|F2B|
=6371+2384=8755.
解得 a=7782.5,c=972.5.
∴b=√a2-c2=√(a+c)(a-c)
=√8755×6810.
≈7722.
∴ 卫星的轨道方程是 P40 探究例3. 如图，一种灯泡的反射镜面是旋转椭圆面的一部分，灯丝位于椭圆的一个焦点F1上，片门位于另一个焦点F2上，由椭圆的焦点F1发出的光线，经过反射后集中到另一个焦点F2。已知BC⊥F1F2，|F1B|=2.8cm , |F1F2|=4.5cm .求截口BAC所在椭圆方程。例4. 点M(x , y)与定点F(4 , 0)的距离和它到直线L : x=25/4的距离的比为常数4/5，求点M的轨迹。（这是椭圆的第二定义）椭圆的第二定义：一个动点到一个定点的距离与它到一条定直线的距离之比为一个常数e(0