江苏省泰州市海陵区2023-2024学年九年级上学期期末数学试题(含答案)
文档属性
| 名称 | 江苏省泰州市海陵区2023-2024学年九年级上学期期末数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 09:21:29 | ||
图片预览




文档简介
海陵区2023~2024学年度第一学期期末学业质量监测试卷
九年级 数学
(考试时间:120分钟,满分150分)
请注意:1.本试卷分为选择题和非选择题两部分.
2.所有试题的答案均填写在答题卡上,答案写在试卷上无效.
3.作图必须用2B铅笔,并请加黑加粗.
第一部分 选择题(共18分)
一、选择题(本大题共6小题,每小题3分,满分18分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,选择正确选项的字母代号涂在答题卡相应的位置上)
1.方程的解是( )
A. B. C., D.,
2.已知的半径为3,点到圆心的距离为4,则点在( )
A.的内部 B.的外部 C.上 D.的内部或上
3.一组数据:,若添加一个数据2,则下列统计量中发生变化的是( )
A.平均数 B.中位数 C.众数 D.极差
4.抛物线与轴的公共点个数为( )
A.0个 B.1个 C.2个 D.3个
5.在中,,,,则的面积等于( )
A.12 B.30 C.37.5 D.24
6.如图,在中,,Ⅰ是的内心,连接并延长至点,使.则的度数是( )
第6题图
A. B. C. D.
第二部分 非选择题(共132分)
二、填空题(本大题共有10小题,每小题3分,满分30分.请把答案直接填写在答题卡相应位置上)
7.根据气象局统计,2023年全年泰州地区最高气温,最低气温,则2023年全年泰州地区气温的极差为______.
8.若,则锐角______
9.已知扇形的圆心角为,半径为,则该扇形的面积为______.(结果保留)
10.黄金分割能让人产生视觉上的美感.某本书的宽与长的比为黄金比(长宽),若该书长为,则宽为______cm.(结果精确到)
11.江豚素有“水中大熊猫”之称,为了解洞庭湖现有江豚数量,考察队先从湖中捕捞10头江豚并做上标记,然后放归湖内.经过一段时间与群体充分混合后,再从中多次捕捞,并算得平均每32头江豚中有2头有标记,则估计洞庭湖现有江豚数量约为______头.
12.若关于的一元二次方程有两个不相等的实数根,则的取值范围是______.
13.如图,已知抛物线与轴交于两点,且与轴交于点,若抛物线上存在点,使得的面积为1,则点的坐标是______.
第13题图
14.如图,点是的重心,连接并延长交于点,易得,过点作,分别交于点,则与面积的比值为______.
第14题图
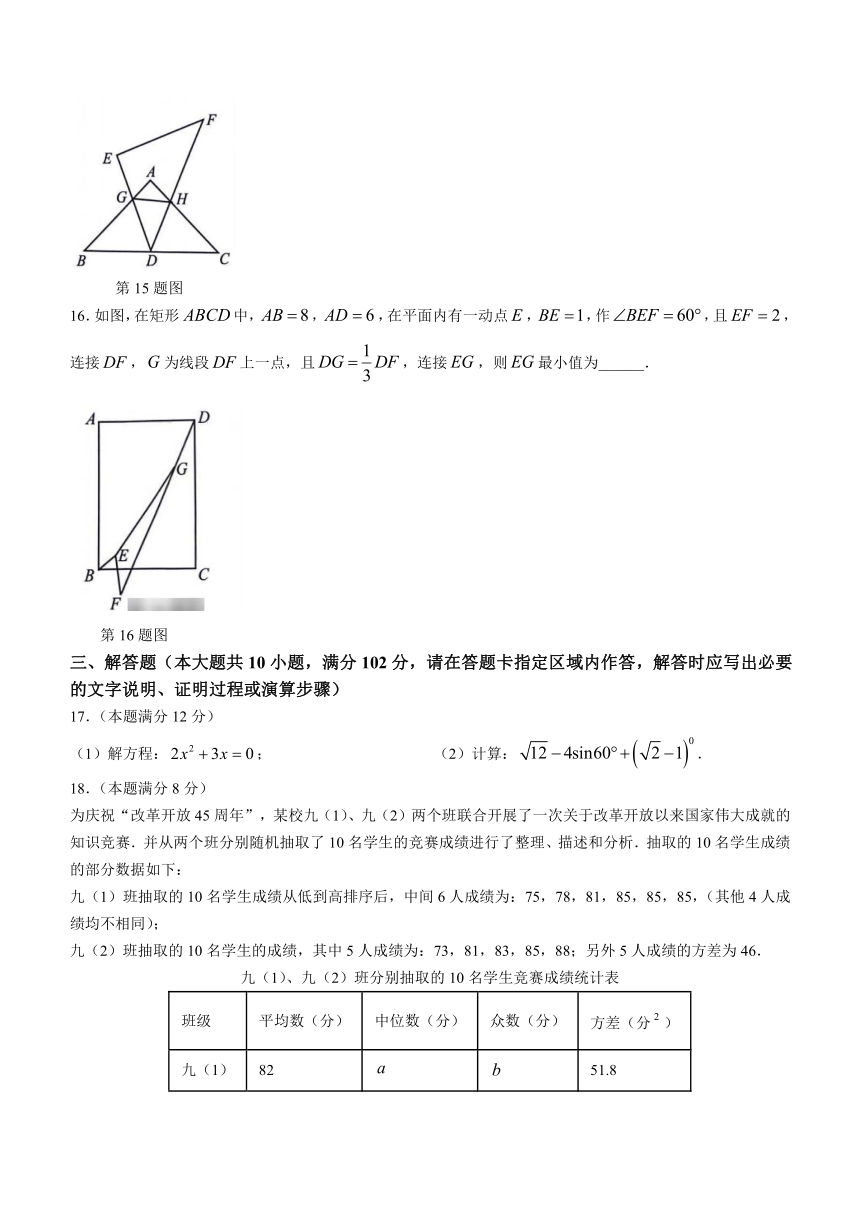
15.和均为等腰直角三角形,按如图所示的方式放置,的顶点与斜边的中点重合,边与边相交于点,若,,,则的面积为______.
第15题图
16.如图,在矩形中,,,在平面内有一动点,,作,且,连接,为线段上一点,且,连接,则最小值为______.
第16题图
三、解答题(本大题共10小题,满分102分,请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本题满分12分)
(1)解方程:; (2)计算:.
18.(本题满分8分)
为庆祝“改革开放45周年”,某校九(1)、九(2)两个班联合开展了一次关于改革开放以来国家伟大成就的知识竞赛.并从两个班分别随机抽取了10名学生的竞赛成绩进行了整理、描述和分析.抽取的10名学生成绩的部分数据如下:
九(1)班抽取的10名学生成绩从低到高排序后,中间6人成绩为:75,78,81,85,85,85,(其他4人成绩均不相同);
九(2)班抽取的10名学生的成绩,其中5人成绩为:73,81,83,85,88;另外5人成绩的方差为46.
九(1)、九(2)班分别抽取的10名学生竞赛成绩统计表
班级 平均数(分) 中位数(分) 众数(分) 方差(分)
九(1) 82 51.8
九(2) 82 84 85
(1)填空:______,______,______;
(2)根据以上随机抽取的数据,你认为本次知识竞赛中,哪个班级学生对改革开放以来国家伟大成就的了解情况更好?请说明理由.
19.(本题满分8分)
“泰州太美,顺风顺水”是泰州的文旅宣传标语.小明、小亮准备采用抽签的方式,各自随机选取泰州的3个景点(A:溱湖湿地公园,B:望海楼,C:老街)中1个景点游玩,3支签分别标有A、B、C.
(1)小明恰好选取A景点的概率为______;
(2)若规定其中一人抽完签后,放回,下一个人再抽,请用列表或树状图的方法,求小明、小亮选取同一景点的概率.
20.(本题满分8分)
某校九年级数学兴趣小组开展“测量建筑物高度”的数学活动,他们设计了一种采用无人机测量教学楼高度的方案:如图,将无人机悬停在距离水平地面28米高的点处,无人机测得楼顶处的俯角为,同时测得地面标记点的俯角为,点在同一平面内,且标记点与教学楼的距离为35米,求教学楼的高度.(结果精确到0.1米,参考数据:,)
第20题图
21.(本题满分10分)
已知:如图,在四边形中,,对角线与相交于点,过点作,交于点.
第21题图
求证:(1); (2).
22.(本题满分10分)
如图,二次函数的图像与轴交于点,且经过点.
第22题图
(1)求此二次函数的表达式,并求出顶点坐标;
(2)若将该二次函数图像先向右平移个单位、再向下平移个单位,平移后的抛物线仍然经过点,求的值.
23.(本题满分10分)
某商场销售一种成本为20元/件的商品,根据市场调查发现:一年内该商品在不同月份的销售单价(元/件)关于月份的函数关系为时,对应各月的销量(件)关于月份的函数关系为.(,且为整数)
(1)2月份该商品销售单价为______元/件,销量为______件;
(2)该商场几月份销售该产品恰好盈利7200元?
(3)请直接写出该商场哪些月份销售该产品当月盈利超过6400元.
24.(本题满分10分)
如图,中,,是的外接圆,的平分线交于点.
图1 图2 图3
第24题
(1)在图1中,仅使用无刻度的直尺作的外角的平分线,与的交点为;(不写作法,保留作图痕迹)
(2)如图2,的外角的平分线交于点,过点作的切线交于点,若,的半径为3,求线段的长;
(3)如图3,的外角的平分线交于点,在图3中仅使用无刻度的直尺作的平分线.(不写作法,保留作图痕迹)
25.(本题满分12分)
在平面直角坐标系中,点是抛物线上的一个动点,点是轴上的一点,作直线交轴正半轴于点.过点的直线交轴于点,交轴于点.作轴于点.
第25题图
(1)当时,求点的坐标;
(2)当时,请结合图像,直接写出的取值范围;
(3)求证:平分.
26.(本题满分14分)
已知:中弦相交于点,连接,作直径,点与点不重合.
初步探索(1)如图1,当时,解决下列问题:
①与是否相等?请说明理由;
②若,,,求的长;
进一步思考
(2)如图2,若是的2倍,求证:点在线段的垂直平分线上;
拓展应用
(3)如图3,若,上存在一个点,满足是的倍(说明:所对圆周角也是所对圆周角的倍),并且,求的值.
图1 图2 图3
第26题图
海陵区2023—2024学年度第一学期期末学业质量监测
九年级数学答案
命题人:李光红、帅建卓、周秀华、顾广林
解答题提供部分解法,其他解法参照给分
一、选择题(每题3分,共18分)
1-6.CBACDB
二、填空题(每题3分,共30分)
7.47 8.60 9. 10.12.4
11.160 12.且 13., 14.
15. 16.
三、解答题
17.(本题满分12分)
(1),; (2)1.
18.(本题满分8分)
(1)填空:83,85,35.8;
(2)在平均数、众数相同的情况下,九(2)班中位数更高,所以九(2)班了解情况更好;
或:在平均数、众数相同的情况下,九(2)班方差更小,成绩更加稳定,所以九(2)班了解情况更好.(回答一条理由即可)
19.(本题满分8分)
(1) (2)树状图或列表略
(小明、小亮选取同一景点)
答:小明、小亮选取同一景点的概率为
20.(本题满分8分)
如图,过点作,垂足为点,过点作,垂足为点.
在中,,,
,即,
在中,,
,即,
答:教学楼的高度约15.9米.
第20题图
21.(本题满分10分)
(1),,
,,,
(2),,
,且,
,,.
22.(本题满分10分)
(1)将点,代入,得,
,,顶点
(2)根据题意,得平移后的抛物线关系式为:,
将代入上式,得,,,
.
23.(本题满分10分)
(1)36,400;
(2)根据题意,得,
解之,得,答:略
(3)3月,4月,5月
24.(本题满分10分)
图1 图2 图3
第24题图
图4
(1)作图痕迹如图1;
(2)平分,平分,
,是的直径,
是的切线,,
,,
平分,,
,,,
,,即,,
其他解法:①作,证明;②作,设,,解得,再证明,.
(3)作图痕迹如图3,连接交于点,连接并延长交于点,作射线即为所求;或如图4,连接并延长交于点,连接交于一点(重心),利用重心确定中点,连接并延长交于点,作射线即为所求
25.(本题满分12分)
(1)当时,点的坐标是,
将,,分别代入中,得:,解得:.所以直线的函数表达式为,于是点的坐标为
(2)
(3)将代入中,得:,所以,代入中,得:,,所以直线的函数表达式为,于是点的坐标为所以,
所以,所以,
又因为轴,轴,所以,所以,
所以,所以,所以平分.
26.(本题满分14分)
(1)①与相等.理由是:
连接,因为是直径,所以,因为,所以,又因为,所以.根据“圆周角的度数等于它所对弧的度数的一半”,可知与相等.
②连接,因为,,,可求得,又可证得,从而求得,由①知与相等,所以,于是求得
或:连接,可得到,进而求得.
(2)取的中点,连接交于,再连接.因为是的2倍,所以,所以,又因为,所以,从而证得,又因为,,所以,所以,所以点在线段的垂直平分线上.
(3)在上取点,连接交于,因为,所以,又因为,所以,因为,所以,所以:
.
根据“圆周角的度数等于它所对弧的度数的一半”,可知:是的3倍,从而是的4倍,所以.
或:设,,
,,
,,,,
,,
在中,,
由点与点不重合,可知.
九年级 数学
(考试时间:120分钟,满分150分)
请注意:1.本试卷分为选择题和非选择题两部分.
2.所有试题的答案均填写在答题卡上,答案写在试卷上无效.
3.作图必须用2B铅笔,并请加黑加粗.
第一部分 选择题(共18分)
一、选择题(本大题共6小题,每小题3分,满分18分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,选择正确选项的字母代号涂在答题卡相应的位置上)
1.方程的解是( )
A. B. C., D.,
2.已知的半径为3,点到圆心的距离为4,则点在( )
A.的内部 B.的外部 C.上 D.的内部或上
3.一组数据:,若添加一个数据2,则下列统计量中发生变化的是( )
A.平均数 B.中位数 C.众数 D.极差
4.抛物线与轴的公共点个数为( )
A.0个 B.1个 C.2个 D.3个
5.在中,,,,则的面积等于( )
A.12 B.30 C.37.5 D.24
6.如图,在中,,Ⅰ是的内心,连接并延长至点,使.则的度数是( )
第6题图
A. B. C. D.
第二部分 非选择题(共132分)
二、填空题(本大题共有10小题,每小题3分,满分30分.请把答案直接填写在答题卡相应位置上)
7.根据气象局统计,2023年全年泰州地区最高气温,最低气温,则2023年全年泰州地区气温的极差为______.
8.若,则锐角______
9.已知扇形的圆心角为,半径为,则该扇形的面积为______.(结果保留)
10.黄金分割能让人产生视觉上的美感.某本书的宽与长的比为黄金比(长宽),若该书长为,则宽为______cm.(结果精确到)
11.江豚素有“水中大熊猫”之称,为了解洞庭湖现有江豚数量,考察队先从湖中捕捞10头江豚并做上标记,然后放归湖内.经过一段时间与群体充分混合后,再从中多次捕捞,并算得平均每32头江豚中有2头有标记,则估计洞庭湖现有江豚数量约为______头.
12.若关于的一元二次方程有两个不相等的实数根,则的取值范围是______.
13.如图,已知抛物线与轴交于两点,且与轴交于点,若抛物线上存在点,使得的面积为1,则点的坐标是______.
第13题图
14.如图,点是的重心,连接并延长交于点,易得,过点作,分别交于点,则与面积的比值为______.
第14题图
15.和均为等腰直角三角形,按如图所示的方式放置,的顶点与斜边的中点重合,边与边相交于点,若,,,则的面积为______.
第15题图
16.如图,在矩形中,,,在平面内有一动点,,作,且,连接,为线段上一点,且,连接,则最小值为______.
第16题图
三、解答题(本大题共10小题,满分102分,请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本题满分12分)
(1)解方程:; (2)计算:.
18.(本题满分8分)
为庆祝“改革开放45周年”,某校九(1)、九(2)两个班联合开展了一次关于改革开放以来国家伟大成就的知识竞赛.并从两个班分别随机抽取了10名学生的竞赛成绩进行了整理、描述和分析.抽取的10名学生成绩的部分数据如下:
九(1)班抽取的10名学生成绩从低到高排序后,中间6人成绩为:75,78,81,85,85,85,(其他4人成绩均不相同);
九(2)班抽取的10名学生的成绩,其中5人成绩为:73,81,83,85,88;另外5人成绩的方差为46.
九(1)、九(2)班分别抽取的10名学生竞赛成绩统计表
班级 平均数(分) 中位数(分) 众数(分) 方差(分)
九(1) 82 51.8
九(2) 82 84 85
(1)填空:______,______,______;
(2)根据以上随机抽取的数据,你认为本次知识竞赛中,哪个班级学生对改革开放以来国家伟大成就的了解情况更好?请说明理由.
19.(本题满分8分)
“泰州太美,顺风顺水”是泰州的文旅宣传标语.小明、小亮准备采用抽签的方式,各自随机选取泰州的3个景点(A:溱湖湿地公园,B:望海楼,C:老街)中1个景点游玩,3支签分别标有A、B、C.
(1)小明恰好选取A景点的概率为______;
(2)若规定其中一人抽完签后,放回,下一个人再抽,请用列表或树状图的方法,求小明、小亮选取同一景点的概率.
20.(本题满分8分)
某校九年级数学兴趣小组开展“测量建筑物高度”的数学活动,他们设计了一种采用无人机测量教学楼高度的方案:如图,将无人机悬停在距离水平地面28米高的点处,无人机测得楼顶处的俯角为,同时测得地面标记点的俯角为,点在同一平面内,且标记点与教学楼的距离为35米,求教学楼的高度.(结果精确到0.1米,参考数据:,)
第20题图
21.(本题满分10分)
已知:如图,在四边形中,,对角线与相交于点,过点作,交于点.
第21题图
求证:(1); (2).
22.(本题满分10分)
如图,二次函数的图像与轴交于点,且经过点.
第22题图
(1)求此二次函数的表达式,并求出顶点坐标;
(2)若将该二次函数图像先向右平移个单位、再向下平移个单位,平移后的抛物线仍然经过点,求的值.
23.(本题满分10分)
某商场销售一种成本为20元/件的商品,根据市场调查发现:一年内该商品在不同月份的销售单价(元/件)关于月份的函数关系为时,对应各月的销量(件)关于月份的函数关系为.(,且为整数)
(1)2月份该商品销售单价为______元/件,销量为______件;
(2)该商场几月份销售该产品恰好盈利7200元?
(3)请直接写出该商场哪些月份销售该产品当月盈利超过6400元.
24.(本题满分10分)
如图,中,,是的外接圆,的平分线交于点.
图1 图2 图3
第24题
(1)在图1中,仅使用无刻度的直尺作的外角的平分线,与的交点为;(不写作法,保留作图痕迹)
(2)如图2,的外角的平分线交于点,过点作的切线交于点,若,的半径为3,求线段的长;
(3)如图3,的外角的平分线交于点,在图3中仅使用无刻度的直尺作的平分线.(不写作法,保留作图痕迹)
25.(本题满分12分)
在平面直角坐标系中,点是抛物线上的一个动点,点是轴上的一点,作直线交轴正半轴于点.过点的直线交轴于点,交轴于点.作轴于点.
第25题图
(1)当时,求点的坐标;
(2)当时,请结合图像,直接写出的取值范围;
(3)求证:平分.
26.(本题满分14分)
已知:中弦相交于点,连接,作直径,点与点不重合.
初步探索(1)如图1,当时,解决下列问题:
①与是否相等?请说明理由;
②若,,,求的长;
进一步思考
(2)如图2,若是的2倍,求证:点在线段的垂直平分线上;
拓展应用
(3)如图3,若,上存在一个点,满足是的倍(说明:所对圆周角也是所对圆周角的倍),并且,求的值.
图1 图2 图3
第26题图
海陵区2023—2024学年度第一学期期末学业质量监测
九年级数学答案
命题人:李光红、帅建卓、周秀华、顾广林
解答题提供部分解法,其他解法参照给分
一、选择题(每题3分,共18分)
1-6.CBACDB
二、填空题(每题3分,共30分)
7.47 8.60 9. 10.12.4
11.160 12.且 13., 14.
15. 16.
三、解答题
17.(本题满分12分)
(1),; (2)1.
18.(本题满分8分)
(1)填空:83,85,35.8;
(2)在平均数、众数相同的情况下,九(2)班中位数更高,所以九(2)班了解情况更好;
或:在平均数、众数相同的情况下,九(2)班方差更小,成绩更加稳定,所以九(2)班了解情况更好.(回答一条理由即可)
19.(本题满分8分)
(1) (2)树状图或列表略
(小明、小亮选取同一景点)
答:小明、小亮选取同一景点的概率为
20.(本题满分8分)
如图,过点作,垂足为点,过点作,垂足为点.
在中,,,
,即,
在中,,
,即,
答:教学楼的高度约15.9米.
第20题图
21.(本题满分10分)
(1),,
,,,
(2),,
,且,
,,.
22.(本题满分10分)
(1)将点,代入,得,
,,顶点
(2)根据题意,得平移后的抛物线关系式为:,
将代入上式,得,,,
.
23.(本题满分10分)
(1)36,400;
(2)根据题意,得,
解之,得,答:略
(3)3月,4月,5月
24.(本题满分10分)
图1 图2 图3
第24题图
图4
(1)作图痕迹如图1;
(2)平分,平分,
,是的直径,
是的切线,,
,,
平分,,
,,,
,,即,,
其他解法:①作,证明;②作,设,,解得,再证明,.
(3)作图痕迹如图3,连接交于点,连接并延长交于点,作射线即为所求;或如图4,连接并延长交于点,连接交于一点(重心),利用重心确定中点,连接并延长交于点,作射线即为所求
25.(本题满分12分)
(1)当时,点的坐标是,
将,,分别代入中,得:,解得:.所以直线的函数表达式为,于是点的坐标为
(2)
(3)将代入中,得:,所以,代入中,得:,,所以直线的函数表达式为,于是点的坐标为所以,
所以,所以,
又因为轴,轴,所以,所以,
所以,所以,所以平分.
26.(本题满分14分)
(1)①与相等.理由是:
连接,因为是直径,所以,因为,所以,又因为,所以.根据“圆周角的度数等于它所对弧的度数的一半”,可知与相等.
②连接,因为,,,可求得,又可证得,从而求得,由①知与相等,所以,于是求得
或:连接,可得到,进而求得.
(2)取的中点,连接交于,再连接.因为是的2倍,所以,所以,又因为,所以,从而证得,又因为,,所以,所以,所以点在线段的垂直平分线上.
(3)在上取点,连接交于,因为,所以,又因为,所以,因为,所以,所以:
.
根据“圆周角的度数等于它所对弧的度数的一半”,可知:是的3倍,从而是的4倍,所以.
或:设,,
,,
,,,,
,,
在中,,
由点与点不重合,可知.
同课章节目录
