§3.集合的基本运算(安徽省阜阳市)
文档属性
| 名称 | §3.集合的基本运算(安徽省阜阳市) |

|
|
| 格式 | rar | ||
| 文件大小 | 616.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-05 00:00:00 | ||
图片预览



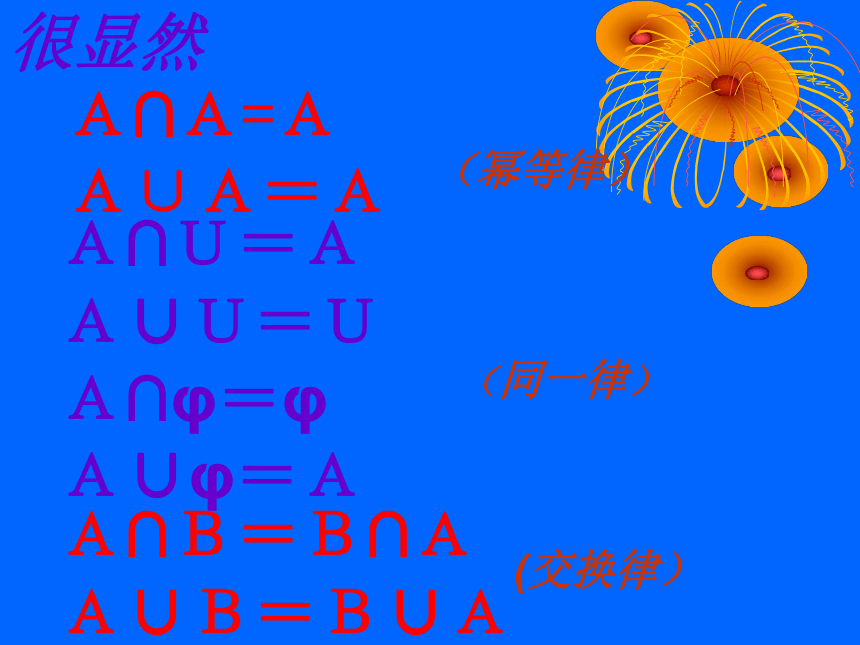
文档简介
课件14张PPT。§3.集合的基本
运算3.1 交集与并集
3.2 全集与补集
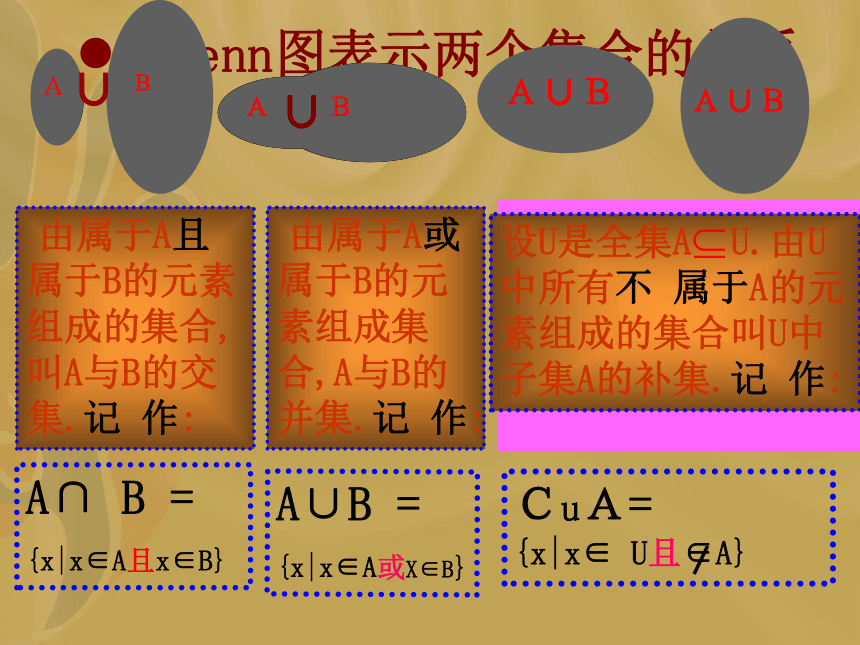
设计者:RSZA用Venn图表示两个集合的关系 由属于A且属于B的元素组成的集合,叫A与B的交集.记 作:A∩ B =
{x|x∈A且x∈B} 由属于A或属于B的元素组成集合,A与B的并集.记 作:A∪B =
{x|x∈A或X∈B}CuA=
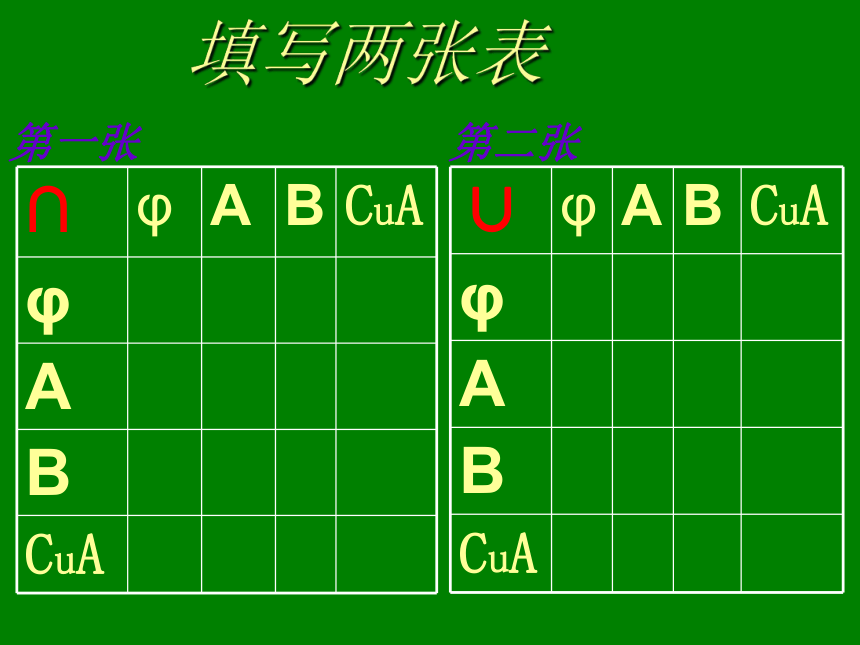
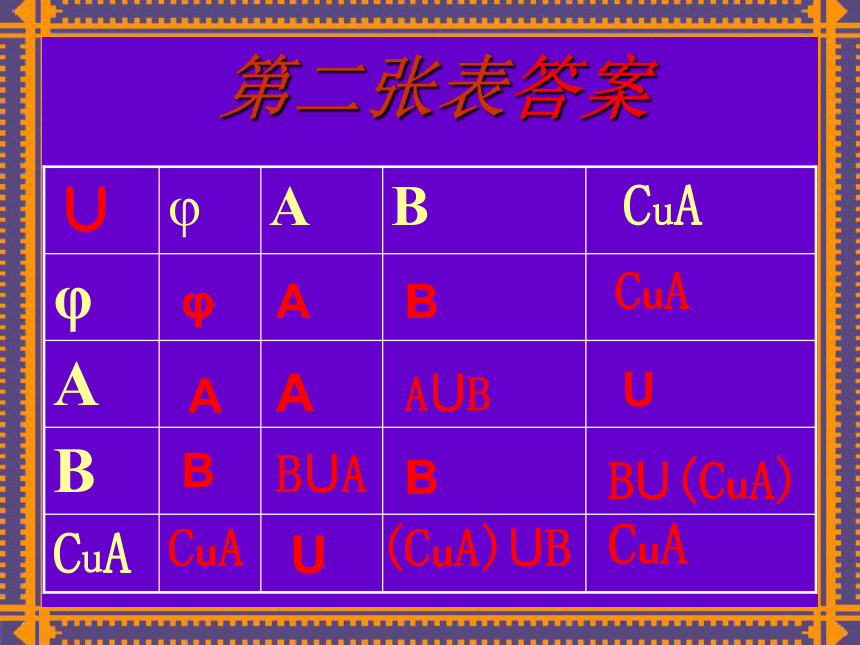
{x|x∈ U且∈A}CuA设U是全集A U.由U中所有不 属于A的元素组成的集合叫U中子集A的补集.记 作:很显然填写两张表第一张 第二张 第一张表的答案φφφφφφφΑφφA∩BB∩AΒ(CuA)∩BB∩(CuA)CuA第二张表答案φΑΑΑΒ
Β
CuAUBUAΒ
AUBUCuABU(CuA)(CuA)UBCuA很显然A∩A=A
A∪A=A(幂等律)A∩U=A
A∪U=U
A∩φ=φ
A∪φ=A(同一律)A∩B=B∩A
A∪B=B∪A(交换律)A∩(CuA)=φ A∪(CuA)=ACuU=φ
Cuφ=U
Cu(CuA)=A(互补律)应用一 设A={a、b、c、d}
B={a、b、e、f、g}
C={b、g、h} 求:
⑴(A∩B)∩C与A∩(B∩C)
⑵(A∪B)∪C与A∪(B∪C)
⑶(A∩B)∪(A∩C)与A∪(B∩C)
⑷(A∪B)∩(A∪C)与A∩(B∪C) ⑸A(A∪B)与A∪(A∩B) 答案:是相等请把这些相等的式子写在笔记本中这些等式依次为(归纳):(A∩B)∩C=A∩(B∩C)=A∩B∩C(A∪B)∪C=A∪(B∪C)=A∪B∪C(结合律)A∩(A∪B)=A∪(A∩B)=A(吸收律)应用二:p13例4题略.解略.归纳 (反演律、狄·摩根定理De Morgan)略图形验证UABUAB可以用维恩图验证其他定律(课外完成)应用三 P16B组2 题略文字语言图形语言符号语言文字语言A15B11A∩B159猜想抽象公式n(A∪B)=n(A)+n(B)-n(A∩B)小结图文并茂理解集合间的三种运算:交、并、补及一些结论.三种语言灵活切换.课外研究题P20A组3、4B组3~6欢迎各位指导
3.2 全集与补集
设计者:RSZA用Venn图表示两个集合的关系 由属于A且属于B的元素组成的集合,叫A与B的交集.记 作:A∩ B =
{x|x∈A且x∈B} 由属于A或属于B的元素组成集合,A与B的并集.记 作:A∪B =
{x|x∈A或X∈B}CuA=
{x|x∈ U且∈A}CuA设U是全集A U.由U中所有不 属于A的元素组成的集合叫U中子集A的补集.记 作:很显然填写两张表第一张 第二张 第一张表的答案φφφφφφφΑφφA∩BB∩AΒ(CuA)∩BB∩(CuA)CuA第二张表答案φΑΑΑΒ
Β
CuAUBUAΒ
AUBUCuABU(CuA)(CuA)UBCuA很显然A∩A=A
A∪A=A(幂等律)A∩U=A
A∪U=U
A∩φ=φ
A∪φ=A(同一律)A∩B=B∩A
A∪B=B∪A(交换律)A∩(CuA)=φ A∪(CuA)=ACuU=φ
Cuφ=U
Cu(CuA)=A(互补律)应用一 设A={a、b、c、d}
B={a、b、e、f、g}
C={b、g、h} 求:
⑴(A∩B)∩C与A∩(B∩C)
⑵(A∪B)∪C与A∪(B∪C)
⑶(A∩B)∪(A∩C)与A∪(B∩C)
⑷(A∪B)∩(A∪C)与A∩(B∪C) ⑸A(A∪B)与A∪(A∩B) 答案:是相等请把这些相等的式子写在笔记本中这些等式依次为(归纳):(A∩B)∩C=A∩(B∩C)=A∩B∩C(A∪B)∪C=A∪(B∪C)=A∪B∪C(结合律)A∩(A∪B)=A∪(A∩B)=A(吸收律)应用二:p13例4题略.解略.归纳 (反演律、狄·摩根定理De Morgan)略图形验证UABUAB可以用维恩图验证其他定律(课外完成)应用三 P16B组2 题略文字语言图形语言符号语言文字语言A15B11A∩B159猜想抽象公式n(A∪B)=n(A)+n(B)-n(A∩B)小结图文并茂理解集合间的三种运算:交、并、补及一些结论.三种语言灵活切换.课外研究题P20A组3、4B组3~6欢迎各位指导
