2024年中考数学高频考点突破——二次函数压轴题(与圆相关)(含答案)
文档属性
| 名称 | 2024年中考数学高频考点突破——二次函数压轴题(与圆相关)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 16:05:38 | ||
图片预览



文档简介
2024年中考数学高频考点突破——二次函数压轴题(与圆相关)
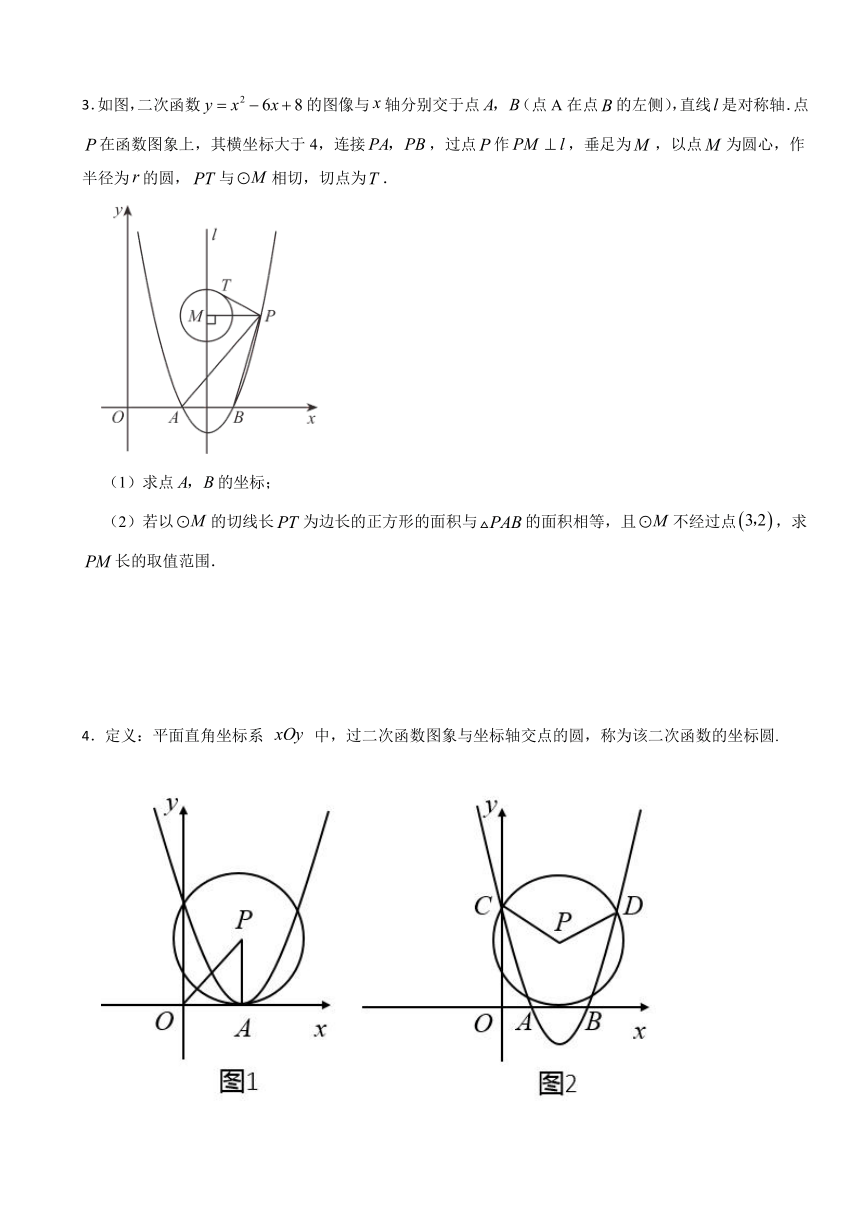
1.在平面直角坐标系中,已知,,且以为直径的圆交y轴的正半轴于点C,过点C作圆的切线交x轴于点D.
(1)求点C的坐标和过A,B,C三点的抛物线的析式;
(2)求点D的坐标:
(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.
2.如图1,我们把一个半圆和抛物线的一部分围成的封闭图形称为“蛋圆”,已知A,B,C,D分别为“蛋圆”与坐标轴的交点,与“蛋圆”中的抛物线 交于B,C两点.
(1)求“蛋圆”中的抛物线的解析式,并直接写出“蛋圆”被y轴截得的线段BD的长.
(2)“蛋圆”上是否存在点P使是等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
(3)如图2,E为直线BC下方“蛋圆”上一点,连结AE,AB,BE,设AE与BC交于F,的面积记为,△ABF的面积记为,求的最小值.
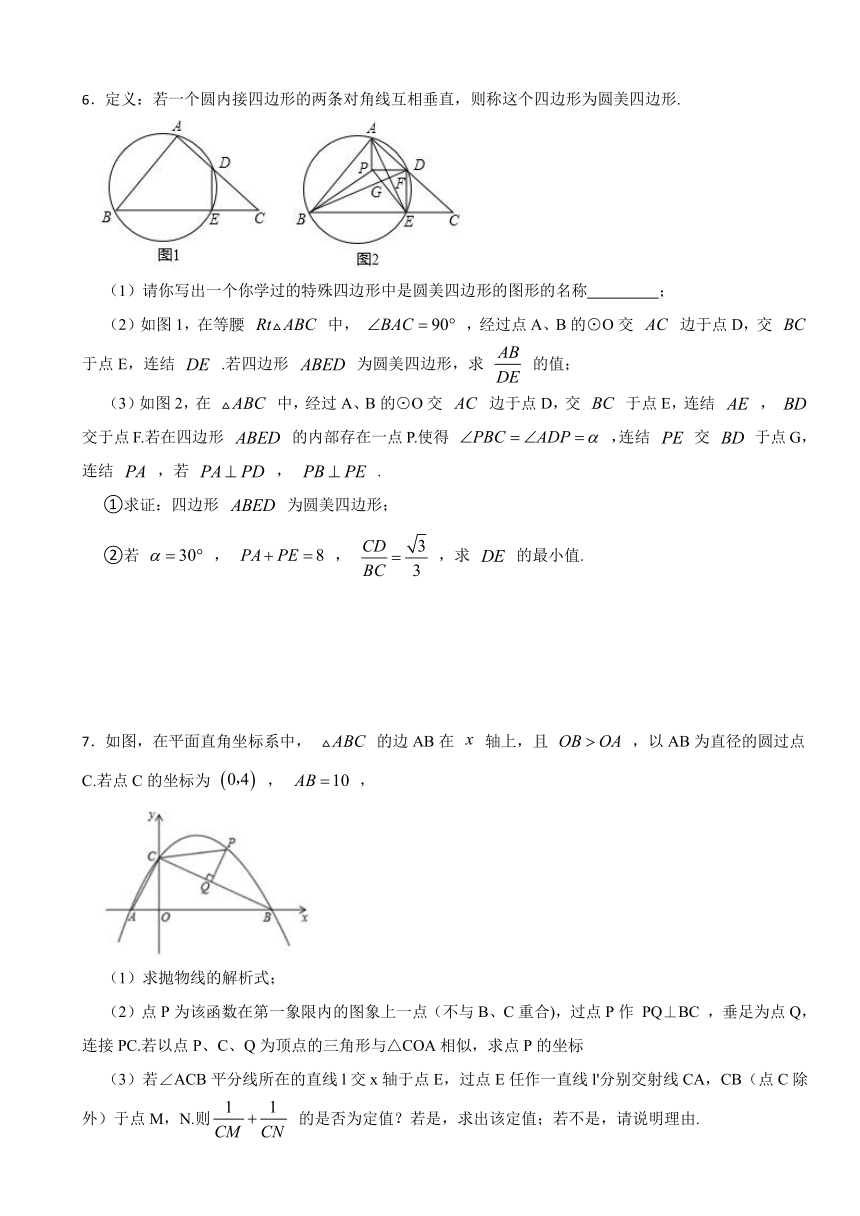
3.如图,二次函数的图像与轴分别交于点(点A在点的左侧),直线是对称轴.点在函数图象上,其横坐标大于4,连接,过点作,垂足为,以点为圆心,作半径为的圆,与相切,切点为.
(1)求点的坐标;
(2)若以的切线长为边长的正方形的面积与的面积相等,且不经过点,求长的取值范围.
4.定义:平面直角坐标系 中,过二次函数图象与坐标轴交点的圆,称为该二次函数的坐标圆.
(1)已知点 ,以 为圆心, 为半径作圆.请判断⊙ 是不是二次函数 的坐标圆,并说明理由;
(2)已知二次函数 图象的顶点为 ,坐标圆的圆心为 ,如图1,求 周长的最小值;
(3)已知二次函数 图象交 轴于点 , ,交 轴于点 ,与坐标圆的第四个交点为 ,连结 , ,如图2.若 ,求 的值.
5.如图,y关于x的二次函数图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以为直径作圆,圆心为C.定点E的坐标为,连接.
(1)写出A、B、D三点的坐标;
(2)当m为何值时M点在直线上?判定此时直线与圆的位置关系;
(3)当m变化时,用m表示的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
6.定义:若一个圆内接四边形的两条对角线互相垂直,则称这个四边形为圆美四边形.
(1)请你写出一个你学过的特殊四边形中是圆美四边形的图形的名称 ;
(2)如图1,在等腰 中, ,经过点A、B的⊙O交 边于点D,交 于点E,连结 .若四边形 为圆美四边形,求 的值;
(3)如图2,在 中,经过A、B的⊙O交 边于点D,交 于点E,连结 , 交于点F.若在四边形 的内部存在一点P.使得 ,连结 交 于点G,连结 ,若 , .
①求证:四边形 为圆美四边形;
②若 , , ,求 的最小值.
7.如图,在平面直角坐标系中, 的边AB在 轴上,且 ,以AB为直径的圆过点C.若点C的坐标为 , ,
(1)求抛物线的解析式;
(2)点P为该函数在第一象限内的图象上一点(不与B、C重合),过点P作 PQ⊥BC ,垂足为点Q,连接PC.若以点P、C、Q为顶点的三角形与△COA相似,求点P的坐标
(3)若∠ACB平分线所在的直线l交x轴于点E,过点E任作一直线l'分别交射线CA,CB(点C除外)于点M,N.则 的是否为定值?若是,求出该定值;若不是,请说明理由.
8.如图,在直角坐标系中,抛物线经过点,,交y轴于点C,以AB为直径的圆,经过点O,C,交x轴于点D,连结AO,AC.
(1)求抛物线的函数表达式;
(2)求点D的坐标;
(3)点E在x轴上,连结BD,BE.当与相似时,求满足条件的OE长.
9.抛物线(a<0,h>0)的图象与x轴相交于A,B两点(A在B的左侧),与y轴相交于点P,顶点为C,以AB为直径的圆恰过顶点C且与y轴的正半轴相交于点Q,
(1)求点A的坐标,并用h的代数式表示a;
(2)当点P是OQ的中点时,求直径AB的长;
(3)如图直线AM垂直AC交抛物线于点M,点T的坐标是(6,0),当以点A,T,C为顶点的三角形与△ABM相似时,求h的值.
10.如图,抛物线交y轴于点,且过点点B是抛物线M上一个动点,过B作,以B为圆心,2为半径的圆交直线于D、E两点(点E位于点D下方)
(1)求抛物线M的解析式;
(2)连接交于点F,连接.若是以为直角边的直角三角形,求的度数;
(3)取的中点Q,连接,求线段的最小值.(直接写出答案)
11.抛物线 (a<0,h>0)的图象与x轴相交于A,B两点(A在B的左侧),与y轴相交于点P,顶点为C,以AB为直径的圆恰过顶点C且与y轴的正半轴相交于点Q,
(1)求点A的坐标,并用h的代数式表示a;
(2)当点P是OQ的中点时,求直径AB的长;
(3)如图直线AM垂直AC交抛物线于点M,点T的坐标是(6,0),当以点A,T,C为顶点的三角形与△ABM相似时,求h的值。
12.如图,已知抛物线 的图象的顶点坐标是 ,并且经过点 ,直线 与抛物线交于 , 两点,以 为直径作圆,圆心为点 ,圆 与直线 交于对称轴右侧的点 ,直线 上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆 与 轴相切;
(3)过点 作 ,垂足为 ,再过点 作 ,垂足为 ,求 的值.(或者求 的值)
13.已知二次函数的图象经过点A(2,0),B(-4,0),C(0,4),点 为二次函数第二象限内抛物线上一动点, 轴于点 ,交直线 于点 ,以 为直径的圆⊙M与 交于点 .
(1)求这个二次函数的关系式;
(2)当三角形 周长最大时.求此时点 点坐标及三角形 的周长;
(3)在(2)的条件下,点N为⊙M上一动点,连接BN,点Q为BN的中点,连接HQ,求HQ的取值范围.
14.在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C,⊙M是△ABC的外接圆.
如图1,若抛物线的顶点D的坐标为(1,4)
(1)求抛物线的解析式,及A、B、C三点的坐标;
(2)求⊙M的半径和圆心M的坐标.
(3)如图2,在x轴上有点P(7,0),试在直线BC上找点Q,使B、Q、P三点构成的三角形与△ABC相似.若存在,请求出Q点坐标;若不存在,请说明理由.
(4)向上平移抛物线y=﹣x2+bx+c,在平移过程中,抛物线与x轴交于A′、B′两点,与y轴交于点C′,则△A′B′C′的外接圆⊙M′是否经过一个定点?若是,请求出这个点的坐标;若不是,请说明理由.
15.如图,已知抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C,⊙M是△ABC的外接圆.若抛物线的顶点D的坐标为(1,4).
(1)求抛物线的解析式,及A、B、C三点的坐标;
(2)求⊙M的半径和圆心M的坐标;
(3)如图2,在x轴上有点P(7,0),试在直线BC上找点Q,使B、Q、P三点构成的三角形与△ABC相似.若存在,请直接写出点坐标;若不存在,请说明理由.
16.如图,抛物线y=ax2﹣x﹣2(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.
答案解析部分
1.【答案】(1)解:设以为直径的圆的圆心为,连结,如图.
∵,,
∴,
∴,
∴,
在中,,
∴点C的坐标为,
由题意,可设所求抛物线的解析式为,把代入,
得,
解得,
∴所求抛物线的解析式为,
即;
(2)解:∵为圆的切线,
∴,
∴.
又∵,
∴
∴,
∴.
即,
∴.
∴点D的坐标为.
(3)解:存在.
抛物线的对称轴为,
设满足条件的圆的半径为r,则点E的坐标为或,
∵点E在抛物线上,
∴,
整理得,
解得(负值,舍去),,
或,
整理得,
解得(负值,舍去),,
∴存在以线段为直径的圆,恰好与x轴相切,该圆的半径为或.
2.【答案】(1)解:∵直线交坐标轴 B,C两点,
∴,,
∵抛物线过B,C两点,
∴,
解得:,
即;
BD=5
(2)解:存在,点P坐标为,,,
(3)解:如图3,
∵,,
∴,
过点E作交x轴于G,
∵的边上的高和的边的高相等,设高为h,
∴,,
∴,
∵的最小值,即最小,
∵,
∴,
∴当最大时,即最小,的最小值,
∴和“蛋圆”的抛物线部分只有一个交点时,最大,
∵直线的解析式为,
设直线EG的解析式为①,
∵抛物线的解析式为即②,
联立①②化简得,,
∴,抛物线和直线只有一个交点.
解得:,
∴直线的解析式为,
∴直线与x轴交点坐标,
∴,
∴,
∴的最小值为.
3.【答案】(1)解:令y=x2-6x+8中的y=0,
则有:x2-6x+8=0,
解得:x1=2,x2=4,
∴A(2,0),B(4,0);
(2)解:∵抛物线过A(2,0),B(4,0)
∴抛物线的对称轴为x=3,
设P(m,m2-6m+8),
∵PM⊥l,
∴M(3,m2-6m+8),
如图:连接MT,则MT⊥PT,
∴,
∴切线PT为边长的正方形的面积为,
过点P作PH⊥x轴,垂足为H,则:,
∴
∵,
∴,
假设过点N(3,2),则有以下两种情况:
①如图1:当点M在点N的上方,即M(3,3),
∴,解得:或,
∵
∴;
②如图2:当点M在点N的下方,即M(3,1),
∴,解得:,
∵
∴;
综上,或.
∴当不经过点时,或或.
4.【答案】(1)解:∵ ,
∴抛物线与坐标轴的交点 , , ,
∵ , , , ,
∴ ,
∴ 是二次函数 的坐标圆
(2)解: ,
∴ , ,
∴过两点 , 的圆的圆心在线段 的中垂线上,
∴ ,
∴ 周长的最小值为6
(3)解:如图所示:连接CD,过P作 于E,PE的反向延长线交AB于F,连接PA
通过图象结合函数及圆的对称性可知:PE与二次函数的对称轴共线, , , .
∵
∴
∴
∵
∴ , ,
∴
令 ,则
解得:
∴
∵ ;
解得:
5.【答案】(1)解:令,则,
解得,;
令,则.
故,,.
(2)解:设直线的解析式为,将,代入得:
解得,,.
直线的解析式为.
将化为顶点式:.
顶点的坐标为.代入得:
,
.所以,当时,M点在直线上.
连接,为中点,C点坐标为.
,,
,D点在圆上
又,,
,,
.
直线与相切.
(3)解:当时,
.
当时,.
即.
S关于m的函数图象的示意图如右:
6.【答案】(1)正方形
(2)解:连结 , ,∵等腰 中, ,
∴ 为⊙O的直径, , ,
∴ ,
∴ ,
∵四边形 为圆美四边形,∴ ,
∴弧 =弧 ,
∴ ,
∴ ,
∴
(3)①证明:∵ , ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
又∵ ,
即
∴ ,
∴ ,
又∵ , ,
∴ 即 ,
∴ ,
又∵A,B,E,D在同一个圆上,
∴四边形 为圆美四边形.
②解:∵ ,∴ ,
∴ ,
∵A,B,E,D在同一个圆上,
∴ ,
∵ ,
∴ ,
∴
设 , , ,
∵ ,
∴ , ,
∴ ,
∴ ,
∵
∴当 时,y2取到最小值32, 的最小值为 .
7.【答案】(1)解:∵以AB为直径的圆过点C,
∴∠ACB=90°,
∵点C的坐标为 ,
∴CO⊥AB,
∴∠AOC=∠COB=90°,
∴∠ACO+∠OCB=∠ACO+∠OAC=90°,
∴∠OCB=∠OAC,
∴ ∽ ,
∴ ,
∵ , ,
∴ ,
∴ ,
解得: 或 ,
经检验,满足题意,
∵ ,
∴ ,
∴点A为( ,0),点B为(8,0).
设抛物线的解析式为 ,把点A、B、C三点的坐标代入,有
,解得: ,
∴抛物线的解析式为 ;
(2)解:根据题意,如图,
当 ∽ 时,
∴ ,
∵ ,
∴ ,
∴PC⊥OC,
∴点P的纵坐标为4,
当 时,有 ,
解得: 或 (舍去);
∴点P的坐标为(6,4);
当 ∽ 时,则此时BC垂直平分OP',作P'G⊥y轴,垂足为G,如上图,
∴ ,
∴AC∥OP',
∴∠ACO=∠P'OG,
∵ ,
∴ ∽ ,
∴ ,
设点P'为( , ),
∴ , ,
∴ ,
解得: ,
∵点P'在第一象限,
∴ ,
∴ ,
∴点P'的坐标为( , );
综合上述,点P的坐标为:(6,4)或( , );
(3)解:过点E作EI⊥AC于I,EJ⊥CN于J,如图:
∵CE是∠ACB的角平分线,
∴EI=EJ,
∵EI∥CN,EJ∥CM,
∴△MEI∽△MNC,△NEJ∽△NMC,
∴ , ,
∴ ,
∴ ,
∴ ,
∵△ACO∽△AEI,
∴ ,
∵ ,
∵ ,
∴ ,
解得: ,经检验,符合题意,
∴ ;
∴ 是一个定值.
8.【答案】(1)解:将点,代入,得
,
解得,
∴抛物线的函数表达式是;
(2)解:连接AD,设点D的坐标为(x,0),
∵AB为圆的直径,
∴,
∴,
∴,
解得x=2或x=0(舍去),
∴点D的坐标为(2,0);
(3)解:∵交y轴于点C,
∴C(0,8),
过点A作AF⊥y轴于F,过点B作BG⊥x轴于G,则F(0,5),G(5,0),
∴,,
∴,
①当△BDE∽△ACO时,如图1,
则,
∵,,
∴,
∴DE=CO=8,
∴OE=OD+DE=2+8=10;
②当△EBD∽△AOC时,如图2,
则,
∵,,OC=8,
∴,
∴DE=,
∴OE=OD+DE=2+=;
综上,OE长为10或.
9.【答案】(1)解:如图,设以AB为直径的圆的圆心为D,连接CD,
由题意知,C(h,h+1),
∴CD=AD=BD=h+1,
OD=h,
∴AO=AD-OD=1,
∴点A的坐标为(-1,0),
把A(-1,0)代入,得,
∴;
(2)解:连接DQ,
则DQ=h+1,
由勾股定理得,
当x=0时,,
∴OP=,
又P为OQ中点,
∴OQ=2OP,
∴,
即
解得(负根舍去),
∴AB=2AD=;
(3)解:过点M作MN⊥AB于点N,
由题意知∠CAT=45°,AC=,AT=7,AB=2(h+1)
又AM⊥AC,
∴∠BAM=45°,
∴∠CAT=∠BAM,
若△ACT和△ABM相似,则有以下两种情形:△ACT∽△ABM和△ACT∽△AMB,
当△ACT∽△ABM时,则,
∴,
∴,
∵MN⊥AN,∠NAM=45°,
∴AN=7,MN=7,
∴ON=6,
∴点M坐标为(6,-7),
代入得,
解得(负根舍去);
当△ACT∽△AMB时,则,
∴,
∴,
∵MN⊥AN,∠NAM=45°,
,
∴
∴点M的坐标为(,),
代入得,
解得(负根舍去).
综上,当或时,以点A,T,C为顶点的三角形与△ABM相似.
10.【答案】(1)解:∵yx2+bx+c交y轴于点A(0,﹣1),且过点P(﹣1,),
∴,
∴,
∴;
(2)解:①∠ABD=90°时,如图1,
∵BE=BF,∠EBF=90°,
∴∠BEF=45°.
②∠ADB=90°时,如图2,
∵AD∥x轴,
∴点D的纵坐标为﹣1,
∵BD=2,
∴点B的纵坐标为﹣3,
将y=﹣3代入,解得x1=x2=﹣2,
所以AD=BD=2,△ABD为等腰直角三角形,
∠BEF22.5°.
综上所述,∠BEF的度数为45°或22.5°;
(3)解:设B(m,m2+2m﹣1),则D(m,m2+2m+1),
∵A(0,﹣1),DQ=AQ,
∴Q(,m2+m),
∵P(﹣1,),
∴当m+1=0时,PQ有最小值,最小值为.
11.【答案】(1)解:由题意得:C点坐标为(h,h+1),
∴OA=h+1-h=1,
∴A(-1,0),
把A(1,0)代入抛物线解析式得: ,
整理得: .
(2)解:如图,取圆心为D点,连接PD,
∵当x=0时,y=ah2+h+1,
∴OP=ah2+h+1,
∴OQ=2OP=2(ah2+h+1),
∵OQ2=OD2+OQ2,
∴(h+1)2=h2+4(ah2+h+1)2,
∴
解得:h=3+2或3-2(舍去),
∴AB=2AD=2(1+3+2)=8+4.
(3)解:如图,过点M作MN⊥AB于点N,
∵∠CAT=45°, AC=(h+1), AT=7,AB=2 (h+1),
又∵AM⊥AC,
∴∠BAM=45°,
∴∠CAT=∠BAM,
若△ACT和△ABM相似,则有以下两种情形:
当 △ACT∽△ABM时,
则,即,
解得:AM=7,
∵MN⊥AN,∠NAM=45° ,
∴AN=7,MN= 7,
∴ON=6,
∴点M坐标为(6,-7),
∴ ,
解得:h=(舍去负根);
当△ACT∽△AMB,
则,即,
∴ ,
∵MN⊥AN,∠NAM=45°,
∴,
∴,
∴点M的坐标为(),
∴,
解得:h=(舍去负根),
综上,h的值为 , .
12.【答案】(1)解:∵已知抛物线 的图象的顶点坐标是 ,
∴可设抛物线解析式为 ,
∵抛物线经过点 ,∴ ,解得 ,
∴抛物线解析式为 ,即 .
(2)证明:联立直线和抛物线解析式可得 ,
解得: 或 ,
∴ , ,
∵ 为 的中点,∴点 的纵坐标为 ,
∵ ,
∴圆的半径为 ,∴点 到 轴的距离等于圆的半径,
∴圆 与 轴相切.
(3)解:如图,过点 作 ,垂足为 ,连接 ,
由(2)知 ,
在 中,由勾股定理求得 ,
∵ ,∴ .
BE=
∴
13.【答案】(1)解:∵抛物线与x轴交于A(2,0),B( ,0)两点,
∴设抛物线的解析式为: ,
由抛物线经过C(0,4),
∴将C(0,4)代入 ,解得: ,
∴抛物线的解析式为: ,
即: ;
(2)解:∵ 轴,
∴FH∥y轴,∠FDE=∠BCO,
∴△FDE∽△BCO,则 ,
根据B( ,0),C(0,4),可得直线BC的解析式为: ,
设 ,则 ,
∴ ,
在△BCO中,OB=OC=4, ,
∴ ,
∴ ,
整理得: ,
∵ ,
∴当 时, 取得最大值,最大值为 ,
将 代入抛物线解析式可得: ,
∴点F的坐标为F( ,4),△EFD的周长为 ;
(3)解:由(2)可知,F( ,4),D(-2,2),
∴H(-2,0),BH=OH,即H为BO的中点,
∵FD为⊙M的直径,
∴M(-2,3),
∵Q为BN的中点,
∴如图所示,连接ON,则HQ为△BON的中位线,
∴ ,即求出ON的取值范围即可,
①∵点N在⊙M运动,
∴当O、M、N三点共线的时候,ON最长,如图所示,
此时,ON=OM+MN,
∵ ,MN=MD=1,
∴ON= ;
②当O、N、M三点共线时,ON最短,如图所示,
此时,ON=OM-MN,即: ,
∴可得ON的取值范围是: ,
∴由 ,得HQ的取值范围是: .
14.【答案】(1)解:∵抛物线y=﹣x2+bx+c的顶点D的坐标为(1,4),
∴ ,解得:,
抛物线的解析式为y=﹣x2+2x+3=﹣(x+1)(x﹣3),
∴A(﹣1,0),B(3,0),C(0,3)
(2)解:连接BC和MB,作MH⊥AB于H,如图1,
则AB=3﹣(﹣1)=4,OC=3,AC= ,BC=3 ,
∴,
设AB=c,BC=a,AC=b,⊙M的半径为R,则由希帕霍斯定理可知:
,
∴R= = ,
∴MB=R= ,
∵MH⊥AB,
∴BH=AH==2,
∴MH= =1,
∴M(1,1);
(3)解:①过点P作PQ1∥AC交CB的延长线于点Q1,如图2,
则△ACB∽△PQ1B,
由A、C两点坐标可求得直线AC的解析式为y=3x+3,
设直线PQ1的解析式为y=3x+m,
将P点坐标(7,0)代入可求得m=﹣21,
∴PQ1的解析式为y=3x﹣21,
由 解得 ,
∴Q1(6,﹣3);
②作∠BPQ2=∠ACB交CB的延长线于点Q2,则:
△ACB∽△Q2PB,且A、C、P、Q2四点共圆,
由相交弦定理可知:AB BP=CB BQ2,
∵AB=4,BC=3 ,BP=4,
∴BQ2=,
作Q2N⊥BP于N,
∵OC=OB,
∴BN=NQ2=,
∴ON=OB+BN=,
∴Q2(,-),
综上,满足要求的Q点坐标为Q1(6,-3),Q2(,-).
(4)解:设平移后的抛物线解析式为y=﹣x2+2x+n,(n>3),则C'(0,n),
令﹣x2+2x+n=0,则x= ,
∴A'(1﹣ ),B'(1+ ),
设△A′B′C′的外接圆⊙M′与y轴的负半轴的交点为E(0,h),
由相交弦定理可知:OC' OE=OA' OB',
∴OE=,
∴E(0,﹣1),
∴△A′B′C′的外接圆⊙M′始终经过一个定点E(0,﹣1).
15.【答案】(1)解:∵抛物线y=-x2+bx+c的顶点D的坐标为(1,4),
∴, 解得
抛物线的解析式为y=-x2+2x+3,
令y=0,则-x2+2x+3=0,解得x=-1或3,
令x=0,y=3,
∴A(-1,0),B(3,0),C(0,3);
(2)解:如图1,连接MB,MC,
∵三角形外心为三边中垂线交点,
∴设M(1,m),
∵MB=MC,
∴
解得m=1,
∴M(1,1),
∴MB=
∴⊙M的半径为,圆心M的坐标为(1,1);
(3)解:由(1)知,,
,
设直线的函数解析式为,
将点代入得:,解得,
则直线的函数解析式为,
设点的坐标为,
则,
要使三点构成的三角形与相似,则或,此时,
,
①当时,
则,即,
解得,
经检验,是原方程的解,
则此时点的坐标为;
②当时,
则,即,
解得,
经检验,是原方程的解,
则此时点的坐标为;
综上,点的坐标为或.
16.【答案】解:(1)将B(4,0)代入抛物线的解析式中,得:
0=16a﹣×4﹣2,即:a=;
∴抛物线的解析式为:y=x2﹣x﹣2.
(2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);
∴OA=1,OC=2,OB=4,
即:OC2=OA OB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(2.5,0).
(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为:y=x﹣2;
设直线l∥BC,则该直线的解析式可表示为:y=x+b,当直线l与抛物线只有一个交点时,可列方程:
x+b=x2﹣x﹣2,即:x2﹣2x﹣2﹣b=0,且△=0;
∴4﹣4×(﹣2﹣b)=0,即b=4;
∴直线l:y=x﹣4.
由于S△MBC=BC×h,当h最大(即点M到直线BC的距离最远)时,△ABC的面积最大
所以点M即直线l和抛物线的唯一交点,有:
,
解得:,
即M(2,﹣3).
1.在平面直角坐标系中,已知,,且以为直径的圆交y轴的正半轴于点C,过点C作圆的切线交x轴于点D.
(1)求点C的坐标和过A,B,C三点的抛物线的析式;
(2)求点D的坐标:
(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.
2.如图1,我们把一个半圆和抛物线的一部分围成的封闭图形称为“蛋圆”,已知A,B,C,D分别为“蛋圆”与坐标轴的交点,与“蛋圆”中的抛物线 交于B,C两点.
(1)求“蛋圆”中的抛物线的解析式,并直接写出“蛋圆”被y轴截得的线段BD的长.
(2)“蛋圆”上是否存在点P使是等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
(3)如图2,E为直线BC下方“蛋圆”上一点,连结AE,AB,BE,设AE与BC交于F,的面积记为,△ABF的面积记为,求的最小值.
3.如图,二次函数的图像与轴分别交于点(点A在点的左侧),直线是对称轴.点在函数图象上,其横坐标大于4,连接,过点作,垂足为,以点为圆心,作半径为的圆,与相切,切点为.
(1)求点的坐标;
(2)若以的切线长为边长的正方形的面积与的面积相等,且不经过点,求长的取值范围.
4.定义:平面直角坐标系 中,过二次函数图象与坐标轴交点的圆,称为该二次函数的坐标圆.
(1)已知点 ,以 为圆心, 为半径作圆.请判断⊙ 是不是二次函数 的坐标圆,并说明理由;
(2)已知二次函数 图象的顶点为 ,坐标圆的圆心为 ,如图1,求 周长的最小值;
(3)已知二次函数 图象交 轴于点 , ,交 轴于点 ,与坐标圆的第四个交点为 ,连结 , ,如图2.若 ,求 的值.
5.如图,y关于x的二次函数图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以为直径作圆,圆心为C.定点E的坐标为,连接.
(1)写出A、B、D三点的坐标;
(2)当m为何值时M点在直线上?判定此时直线与圆的位置关系;
(3)当m变化时,用m表示的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
6.定义:若一个圆内接四边形的两条对角线互相垂直,则称这个四边形为圆美四边形.
(1)请你写出一个你学过的特殊四边形中是圆美四边形的图形的名称 ;
(2)如图1,在等腰 中, ,经过点A、B的⊙O交 边于点D,交 于点E,连结 .若四边形 为圆美四边形,求 的值;
(3)如图2,在 中,经过A、B的⊙O交 边于点D,交 于点E,连结 , 交于点F.若在四边形 的内部存在一点P.使得 ,连结 交 于点G,连结 ,若 , .
①求证:四边形 为圆美四边形;
②若 , , ,求 的最小值.
7.如图,在平面直角坐标系中, 的边AB在 轴上,且 ,以AB为直径的圆过点C.若点C的坐标为 , ,
(1)求抛物线的解析式;
(2)点P为该函数在第一象限内的图象上一点(不与B、C重合),过点P作 PQ⊥BC ,垂足为点Q,连接PC.若以点P、C、Q为顶点的三角形与△COA相似,求点P的坐标
(3)若∠ACB平分线所在的直线l交x轴于点E,过点E任作一直线l'分别交射线CA,CB(点C除外)于点M,N.则 的是否为定值?若是,求出该定值;若不是,请说明理由.
8.如图,在直角坐标系中,抛物线经过点,,交y轴于点C,以AB为直径的圆,经过点O,C,交x轴于点D,连结AO,AC.
(1)求抛物线的函数表达式;
(2)求点D的坐标;
(3)点E在x轴上,连结BD,BE.当与相似时,求满足条件的OE长.
9.抛物线(a<0,h>0)的图象与x轴相交于A,B两点(A在B的左侧),与y轴相交于点P,顶点为C,以AB为直径的圆恰过顶点C且与y轴的正半轴相交于点Q,
(1)求点A的坐标,并用h的代数式表示a;
(2)当点P是OQ的中点时,求直径AB的长;
(3)如图直线AM垂直AC交抛物线于点M,点T的坐标是(6,0),当以点A,T,C为顶点的三角形与△ABM相似时,求h的值.
10.如图,抛物线交y轴于点,且过点点B是抛物线M上一个动点,过B作,以B为圆心,2为半径的圆交直线于D、E两点(点E位于点D下方)
(1)求抛物线M的解析式;
(2)连接交于点F,连接.若是以为直角边的直角三角形,求的度数;
(3)取的中点Q,连接,求线段的最小值.(直接写出答案)
11.抛物线 (a<0,h>0)的图象与x轴相交于A,B两点(A在B的左侧),与y轴相交于点P,顶点为C,以AB为直径的圆恰过顶点C且与y轴的正半轴相交于点Q,
(1)求点A的坐标,并用h的代数式表示a;
(2)当点P是OQ的中点时,求直径AB的长;
(3)如图直线AM垂直AC交抛物线于点M,点T的坐标是(6,0),当以点A,T,C为顶点的三角形与△ABM相似时,求h的值。
12.如图,已知抛物线 的图象的顶点坐标是 ,并且经过点 ,直线 与抛物线交于 , 两点,以 为直径作圆,圆心为点 ,圆 与直线 交于对称轴右侧的点 ,直线 上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆 与 轴相切;
(3)过点 作 ,垂足为 ,再过点 作 ,垂足为 ,求 的值.(或者求 的值)
13.已知二次函数的图象经过点A(2,0),B(-4,0),C(0,4),点 为二次函数第二象限内抛物线上一动点, 轴于点 ,交直线 于点 ,以 为直径的圆⊙M与 交于点 .
(1)求这个二次函数的关系式;
(2)当三角形 周长最大时.求此时点 点坐标及三角形 的周长;
(3)在(2)的条件下,点N为⊙M上一动点,连接BN,点Q为BN的中点,连接HQ,求HQ的取值范围.
14.在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C,⊙M是△ABC的外接圆.
如图1,若抛物线的顶点D的坐标为(1,4)
(1)求抛物线的解析式,及A、B、C三点的坐标;
(2)求⊙M的半径和圆心M的坐标.
(3)如图2,在x轴上有点P(7,0),试在直线BC上找点Q,使B、Q、P三点构成的三角形与△ABC相似.若存在,请求出Q点坐标;若不存在,请说明理由.
(4)向上平移抛物线y=﹣x2+bx+c,在平移过程中,抛物线与x轴交于A′、B′两点,与y轴交于点C′,则△A′B′C′的外接圆⊙M′是否经过一个定点?若是,请求出这个点的坐标;若不是,请说明理由.
15.如图,已知抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C,⊙M是△ABC的外接圆.若抛物线的顶点D的坐标为(1,4).
(1)求抛物线的解析式,及A、B、C三点的坐标;
(2)求⊙M的半径和圆心M的坐标;
(3)如图2,在x轴上有点P(7,0),试在直线BC上找点Q,使B、Q、P三点构成的三角形与△ABC相似.若存在,请直接写出点坐标;若不存在,请说明理由.
16.如图,抛物线y=ax2﹣x﹣2(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.
答案解析部分
1.【答案】(1)解:设以为直径的圆的圆心为,连结,如图.
∵,,
∴,
∴,
∴,
在中,,
∴点C的坐标为,
由题意,可设所求抛物线的解析式为,把代入,
得,
解得,
∴所求抛物线的解析式为,
即;
(2)解:∵为圆的切线,
∴,
∴.
又∵,
∴
∴,
∴.
即,
∴.
∴点D的坐标为.
(3)解:存在.
抛物线的对称轴为,
设满足条件的圆的半径为r,则点E的坐标为或,
∵点E在抛物线上,
∴,
整理得,
解得(负值,舍去),,
或,
整理得,
解得(负值,舍去),,
∴存在以线段为直径的圆,恰好与x轴相切,该圆的半径为或.
2.【答案】(1)解:∵直线交坐标轴 B,C两点,
∴,,
∵抛物线过B,C两点,
∴,
解得:,
即;
BD=5
(2)解:存在,点P坐标为,,,
(3)解:如图3,
∵,,
∴,
过点E作交x轴于G,
∵的边上的高和的边的高相等,设高为h,
∴,,
∴,
∵的最小值,即最小,
∵,
∴,
∴当最大时,即最小,的最小值,
∴和“蛋圆”的抛物线部分只有一个交点时,最大,
∵直线的解析式为,
设直线EG的解析式为①,
∵抛物线的解析式为即②,
联立①②化简得,,
∴,抛物线和直线只有一个交点.
解得:,
∴直线的解析式为,
∴直线与x轴交点坐标,
∴,
∴,
∴的最小值为.
3.【答案】(1)解:令y=x2-6x+8中的y=0,
则有:x2-6x+8=0,
解得:x1=2,x2=4,
∴A(2,0),B(4,0);
(2)解:∵抛物线过A(2,0),B(4,0)
∴抛物线的对称轴为x=3,
设P(m,m2-6m+8),
∵PM⊥l,
∴M(3,m2-6m+8),
如图:连接MT,则MT⊥PT,
∴,
∴切线PT为边长的正方形的面积为,
过点P作PH⊥x轴,垂足为H,则:,
∴
∵,
∴,
假设过点N(3,2),则有以下两种情况:
①如图1:当点M在点N的上方,即M(3,3),
∴,解得:或,
∵
∴;
②如图2:当点M在点N的下方,即M(3,1),
∴,解得:,
∵
∴;
综上,或.
∴当不经过点时,或或.
4.【答案】(1)解:∵ ,
∴抛物线与坐标轴的交点 , , ,
∵ , , , ,
∴ ,
∴ 是二次函数 的坐标圆
(2)解: ,
∴ , ,
∴过两点 , 的圆的圆心在线段 的中垂线上,
∴ ,
∴ 周长的最小值为6
(3)解:如图所示:连接CD,过P作 于E,PE的反向延长线交AB于F,连接PA
通过图象结合函数及圆的对称性可知:PE与二次函数的对称轴共线, , , .
∵
∴
∴
∵
∴ , ,
∴
令 ,则
解得:
∴
∵ ;
解得:
5.【答案】(1)解:令,则,
解得,;
令,则.
故,,.
(2)解:设直线的解析式为,将,代入得:
解得,,.
直线的解析式为.
将化为顶点式:.
顶点的坐标为.代入得:
,
.所以,当时,M点在直线上.
连接,为中点,C点坐标为.
,,
,D点在圆上
又,,
,,
.
直线与相切.
(3)解:当时,
.
当时,.
即.
S关于m的函数图象的示意图如右:
6.【答案】(1)正方形
(2)解:连结 , ,∵等腰 中, ,
∴ 为⊙O的直径, , ,
∴ ,
∴ ,
∵四边形 为圆美四边形,∴ ,
∴弧 =弧 ,
∴ ,
∴ ,
∴
(3)①证明:∵ , ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
又∵ ,
即
∴ ,
∴ ,
又∵ , ,
∴ 即 ,
∴ ,
又∵A,B,E,D在同一个圆上,
∴四边形 为圆美四边形.
②解:∵ ,∴ ,
∴ ,
∵A,B,E,D在同一个圆上,
∴ ,
∵ ,
∴ ,
∴
设 , , ,
∵ ,
∴ , ,
∴ ,
∴ ,
∵
∴当 时,y2取到最小值32, 的最小值为 .
7.【答案】(1)解:∵以AB为直径的圆过点C,
∴∠ACB=90°,
∵点C的坐标为 ,
∴CO⊥AB,
∴∠AOC=∠COB=90°,
∴∠ACO+∠OCB=∠ACO+∠OAC=90°,
∴∠OCB=∠OAC,
∴ ∽ ,
∴ ,
∵ , ,
∴ ,
∴ ,
解得: 或 ,
经检验,满足题意,
∵ ,
∴ ,
∴点A为( ,0),点B为(8,0).
设抛物线的解析式为 ,把点A、B、C三点的坐标代入,有
,解得: ,
∴抛物线的解析式为 ;
(2)解:根据题意,如图,
当 ∽ 时,
∴ ,
∵ ,
∴ ,
∴PC⊥OC,
∴点P的纵坐标为4,
当 时,有 ,
解得: 或 (舍去);
∴点P的坐标为(6,4);
当 ∽ 时,则此时BC垂直平分OP',作P'G⊥y轴,垂足为G,如上图,
∴ ,
∴AC∥OP',
∴∠ACO=∠P'OG,
∵ ,
∴ ∽ ,
∴ ,
设点P'为( , ),
∴ , ,
∴ ,
解得: ,
∵点P'在第一象限,
∴ ,
∴ ,
∴点P'的坐标为( , );
综合上述,点P的坐标为:(6,4)或( , );
(3)解:过点E作EI⊥AC于I,EJ⊥CN于J,如图:
∵CE是∠ACB的角平分线,
∴EI=EJ,
∵EI∥CN,EJ∥CM,
∴△MEI∽△MNC,△NEJ∽△NMC,
∴ , ,
∴ ,
∴ ,
∴ ,
∵△ACO∽△AEI,
∴ ,
∵ ,
∵ ,
∴ ,
解得: ,经检验,符合题意,
∴ ;
∴ 是一个定值.
8.【答案】(1)解:将点,代入,得
,
解得,
∴抛物线的函数表达式是;
(2)解:连接AD,设点D的坐标为(x,0),
∵AB为圆的直径,
∴,
∴,
∴,
解得x=2或x=0(舍去),
∴点D的坐标为(2,0);
(3)解:∵交y轴于点C,
∴C(0,8),
过点A作AF⊥y轴于F,过点B作BG⊥x轴于G,则F(0,5),G(5,0),
∴,,
∴,
①当△BDE∽△ACO时,如图1,
则,
∵,,
∴,
∴DE=CO=8,
∴OE=OD+DE=2+8=10;
②当△EBD∽△AOC时,如图2,
则,
∵,,OC=8,
∴,
∴DE=,
∴OE=OD+DE=2+=;
综上,OE长为10或.
9.【答案】(1)解:如图,设以AB为直径的圆的圆心为D,连接CD,
由题意知,C(h,h+1),
∴CD=AD=BD=h+1,
OD=h,
∴AO=AD-OD=1,
∴点A的坐标为(-1,0),
把A(-1,0)代入,得,
∴;
(2)解:连接DQ,
则DQ=h+1,
由勾股定理得,
当x=0时,,
∴OP=,
又P为OQ中点,
∴OQ=2OP,
∴,
即
解得(负根舍去),
∴AB=2AD=;
(3)解:过点M作MN⊥AB于点N,
由题意知∠CAT=45°,AC=,AT=7,AB=2(h+1)
又AM⊥AC,
∴∠BAM=45°,
∴∠CAT=∠BAM,
若△ACT和△ABM相似,则有以下两种情形:△ACT∽△ABM和△ACT∽△AMB,
当△ACT∽△ABM时,则,
∴,
∴,
∵MN⊥AN,∠NAM=45°,
∴AN=7,MN=7,
∴ON=6,
∴点M坐标为(6,-7),
代入得,
解得(负根舍去);
当△ACT∽△AMB时,则,
∴,
∴,
∵MN⊥AN,∠NAM=45°,
,
∴
∴点M的坐标为(,),
代入得,
解得(负根舍去).
综上,当或时,以点A,T,C为顶点的三角形与△ABM相似.
10.【答案】(1)解:∵yx2+bx+c交y轴于点A(0,﹣1),且过点P(﹣1,),
∴,
∴,
∴;
(2)解:①∠ABD=90°时,如图1,
∵BE=BF,∠EBF=90°,
∴∠BEF=45°.
②∠ADB=90°时,如图2,
∵AD∥x轴,
∴点D的纵坐标为﹣1,
∵BD=2,
∴点B的纵坐标为﹣3,
将y=﹣3代入,解得x1=x2=﹣2,
所以AD=BD=2,△ABD为等腰直角三角形,
∠BEF22.5°.
综上所述,∠BEF的度数为45°或22.5°;
(3)解:设B(m,m2+2m﹣1),则D(m,m2+2m+1),
∵A(0,﹣1),DQ=AQ,
∴Q(,m2+m),
∵P(﹣1,),
∴当m+1=0时,PQ有最小值,最小值为.
11.【答案】(1)解:由题意得:C点坐标为(h,h+1),
∴OA=h+1-h=1,
∴A(-1,0),
把A(1,0)代入抛物线解析式得: ,
整理得: .
(2)解:如图,取圆心为D点,连接PD,
∵当x=0时,y=ah2+h+1,
∴OP=ah2+h+1,
∴OQ=2OP=2(ah2+h+1),
∵OQ2=OD2+OQ2,
∴(h+1)2=h2+4(ah2+h+1)2,
∴
解得:h=3+2或3-2(舍去),
∴AB=2AD=2(1+3+2)=8+4.
(3)解:如图,过点M作MN⊥AB于点N,
∵∠CAT=45°, AC=(h+1), AT=7,AB=2 (h+1),
又∵AM⊥AC,
∴∠BAM=45°,
∴∠CAT=∠BAM,
若△ACT和△ABM相似,则有以下两种情形:
当 △ACT∽△ABM时,
则,即,
解得:AM=7,
∵MN⊥AN,∠NAM=45° ,
∴AN=7,MN= 7,
∴ON=6,
∴点M坐标为(6,-7),
∴ ,
解得:h=(舍去负根);
当△ACT∽△AMB,
则,即,
∴ ,
∵MN⊥AN,∠NAM=45°,
∴,
∴,
∴点M的坐标为(),
∴,
解得:h=(舍去负根),
综上,h的值为 , .
12.【答案】(1)解:∵已知抛物线 的图象的顶点坐标是 ,
∴可设抛物线解析式为 ,
∵抛物线经过点 ,∴ ,解得 ,
∴抛物线解析式为 ,即 .
(2)证明:联立直线和抛物线解析式可得 ,
解得: 或 ,
∴ , ,
∵ 为 的中点,∴点 的纵坐标为 ,
∵ ,
∴圆的半径为 ,∴点 到 轴的距离等于圆的半径,
∴圆 与 轴相切.
(3)解:如图,过点 作 ,垂足为 ,连接 ,
由(2)知 ,
在 中,由勾股定理求得 ,
∵ ,∴ .
BE=
∴
13.【答案】(1)解:∵抛物线与x轴交于A(2,0),B( ,0)两点,
∴设抛物线的解析式为: ,
由抛物线经过C(0,4),
∴将C(0,4)代入 ,解得: ,
∴抛物线的解析式为: ,
即: ;
(2)解:∵ 轴,
∴FH∥y轴,∠FDE=∠BCO,
∴△FDE∽△BCO,则 ,
根据B( ,0),C(0,4),可得直线BC的解析式为: ,
设 ,则 ,
∴ ,
在△BCO中,OB=OC=4, ,
∴ ,
∴ ,
整理得: ,
∵ ,
∴当 时, 取得最大值,最大值为 ,
将 代入抛物线解析式可得: ,
∴点F的坐标为F( ,4),△EFD的周长为 ;
(3)解:由(2)可知,F( ,4),D(-2,2),
∴H(-2,0),BH=OH,即H为BO的中点,
∵FD为⊙M的直径,
∴M(-2,3),
∵Q为BN的中点,
∴如图所示,连接ON,则HQ为△BON的中位线,
∴ ,即求出ON的取值范围即可,
①∵点N在⊙M运动,
∴当O、M、N三点共线的时候,ON最长,如图所示,
此时,ON=OM+MN,
∵ ,MN=MD=1,
∴ON= ;
②当O、N、M三点共线时,ON最短,如图所示,
此时,ON=OM-MN,即: ,
∴可得ON的取值范围是: ,
∴由 ,得HQ的取值范围是: .
14.【答案】(1)解:∵抛物线y=﹣x2+bx+c的顶点D的坐标为(1,4),
∴ ,解得:,
抛物线的解析式为y=﹣x2+2x+3=﹣(x+1)(x﹣3),
∴A(﹣1,0),B(3,0),C(0,3)
(2)解:连接BC和MB,作MH⊥AB于H,如图1,
则AB=3﹣(﹣1)=4,OC=3,AC= ,BC=3 ,
∴,
设AB=c,BC=a,AC=b,⊙M的半径为R,则由希帕霍斯定理可知:
,
∴R= = ,
∴MB=R= ,
∵MH⊥AB,
∴BH=AH==2,
∴MH= =1,
∴M(1,1);
(3)解:①过点P作PQ1∥AC交CB的延长线于点Q1,如图2,
则△ACB∽△PQ1B,
由A、C两点坐标可求得直线AC的解析式为y=3x+3,
设直线PQ1的解析式为y=3x+m,
将P点坐标(7,0)代入可求得m=﹣21,
∴PQ1的解析式为y=3x﹣21,
由 解得 ,
∴Q1(6,﹣3);
②作∠BPQ2=∠ACB交CB的延长线于点Q2,则:
△ACB∽△Q2PB,且A、C、P、Q2四点共圆,
由相交弦定理可知:AB BP=CB BQ2,
∵AB=4,BC=3 ,BP=4,
∴BQ2=,
作Q2N⊥BP于N,
∵OC=OB,
∴BN=NQ2=,
∴ON=OB+BN=,
∴Q2(,-),
综上,满足要求的Q点坐标为Q1(6,-3),Q2(,-).
(4)解:设平移后的抛物线解析式为y=﹣x2+2x+n,(n>3),则C'(0,n),
令﹣x2+2x+n=0,则x= ,
∴A'(1﹣ ),B'(1+ ),
设△A′B′C′的外接圆⊙M′与y轴的负半轴的交点为E(0,h),
由相交弦定理可知:OC' OE=OA' OB',
∴OE=,
∴E(0,﹣1),
∴△A′B′C′的外接圆⊙M′始终经过一个定点E(0,﹣1).
15.【答案】(1)解:∵抛物线y=-x2+bx+c的顶点D的坐标为(1,4),
∴, 解得
抛物线的解析式为y=-x2+2x+3,
令y=0,则-x2+2x+3=0,解得x=-1或3,
令x=0,y=3,
∴A(-1,0),B(3,0),C(0,3);
(2)解:如图1,连接MB,MC,
∵三角形外心为三边中垂线交点,
∴设M(1,m),
∵MB=MC,
∴
解得m=1,
∴M(1,1),
∴MB=
∴⊙M的半径为,圆心M的坐标为(1,1);
(3)解:由(1)知,,
,
设直线的函数解析式为,
将点代入得:,解得,
则直线的函数解析式为,
设点的坐标为,
则,
要使三点构成的三角形与相似,则或,此时,
,
①当时,
则,即,
解得,
经检验,是原方程的解,
则此时点的坐标为;
②当时,
则,即,
解得,
经检验,是原方程的解,
则此时点的坐标为;
综上,点的坐标为或.
16.【答案】解:(1)将B(4,0)代入抛物线的解析式中,得:
0=16a﹣×4﹣2,即:a=;
∴抛物线的解析式为:y=x2﹣x﹣2.
(2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);
∴OA=1,OC=2,OB=4,
即:OC2=OA OB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(2.5,0).
(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为:y=x﹣2;
设直线l∥BC,则该直线的解析式可表示为:y=x+b,当直线l与抛物线只有一个交点时,可列方程:
x+b=x2﹣x﹣2,即:x2﹣2x﹣2﹣b=0,且△=0;
∴4﹣4×(﹣2﹣b)=0,即b=4;
∴直线l:y=x﹣4.
由于S△MBC=BC×h,当h最大(即点M到直线BC的距离最远)时,△ABC的面积最大
所以点M即直线l和抛物线的唯一交点,有:
,
解得:,
即M(2,﹣3).
同课章节目录
