2015秋 九年级数学(上)(湘教版)第1章反比例函数检测题
文档属性
| 名称 | 2015秋 九年级数学(上)(湘教版)第1章反比例函数检测题 |  | |
| 格式 | zip | ||
| 文件大小 | 882.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-07 15:57:20 | ||
图片预览


文档简介
第1章 反比例函数检测题
(满分:100分,时间:90分钟)
一、选择题(每小题3分,共30分)
1. .( 2015·天津中考)已知反比例函数y=,当1A.06
2.函数的图象经过点,则函数的图象不经过第( )象限.
A .一 B.二 C.三 D.四
3.在同一直角坐标系中,函数和的图象大致是( )
4. (2015·山东青岛中考)如图,正比例函数的图象与反比例函数的图象相交于A、B两点,其中点A的横坐标为2,当时,的取值范围是( )
A.x<-2或x>2 B.x<-2或0C.-22
5.购买只茶杯需15元,则购买茶杯的单价与的关系式为( )
A. (取实数) B. (取整数)
C. (取自然数) D. (取正整数)
6.若反比例函数的图象位于第二、四象限,则的值是( )
A. 0 B.0或1 C.0或2 D.4
7.(2015·浙江温州中考)如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限.若反比例函数的图象经过点B,则的值是( )
A. 1 B. 2 C. D.
8. 在函数(a为常数)的图象上有三点(-3,y1),(-1,y2),(2,y3),则函数值y1,y2,y3的大小关系是( )
A. B.
C. D.
9. (2015 江苏连云港中考)如图,O为坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=(x<0)的图象经过顶点B,则k的值为( )
A. -12 B. -27 C. -32 D. -36
10.(2014·福州中考) 如图,已知直线yx2分别与x轴、y轴交于A,B两点,与双曲线y交于E,F两点,若AB2EF,则k的值是( )
A.1 B.1 C. D.
二、填空题(每小题3分,共24分)
11. (2015·福州中考)一个反比例函数图象过点A(2,3),则这个反比例函数的解析式是________.
12. 若点在反比例函数的图象上,则当函数值时,自变量x的取值范围是___________.
13.已知反比例函数,当时,其图象的两个分支在第一、三象限内;当时,其图象在每个象限内随的增大而增大.
14.若反比例函数的图象位于第一、三象限内,正比例函数的图象过第二、四象限,则的整数值是________.
15.现有一批救灾物资要从A市运往B市,如果两市的距离为500千米,车速为每小时千米,从A市到B市所需时间为小时,那么与之间的函数关系式为_________,是的________ 函数.
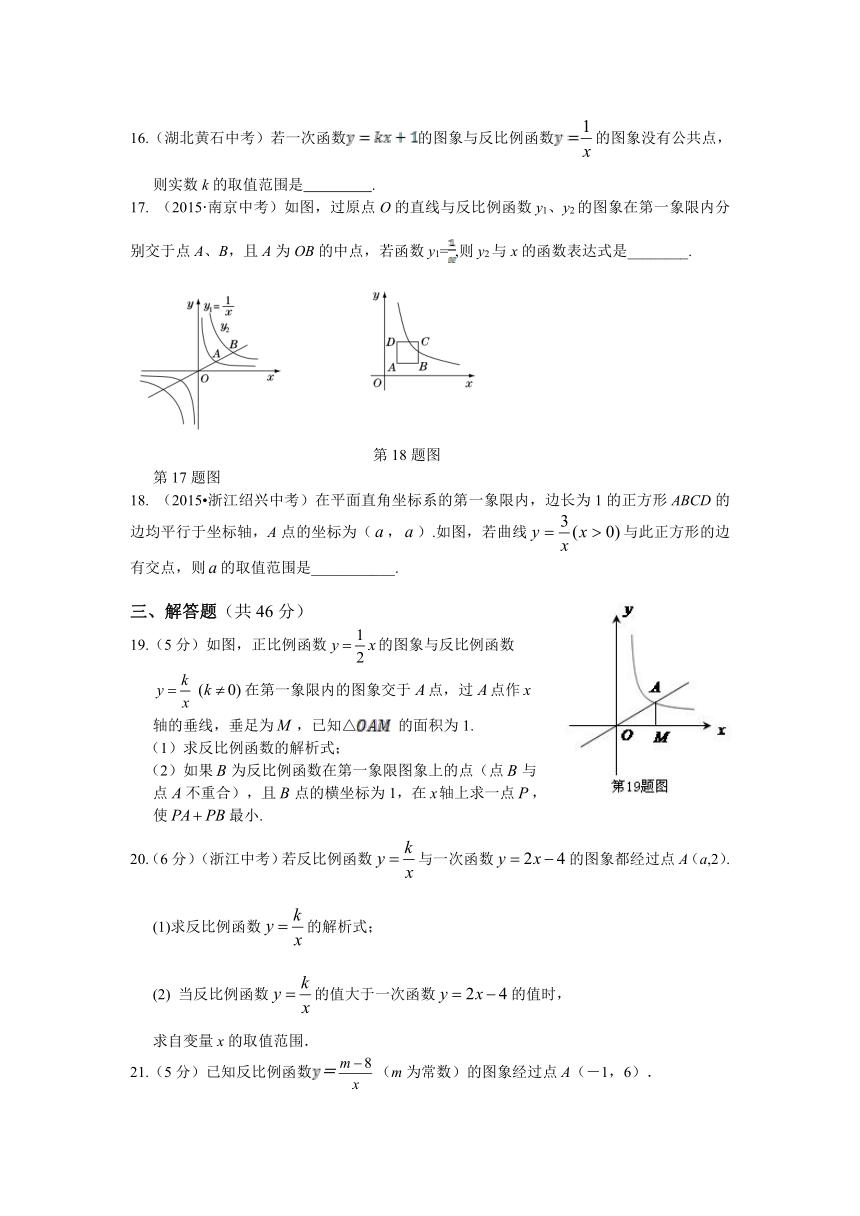
16.(湖北黄石中考)若一次函数的图象与反比例函数的图象没有公共点,则实数k的取值范围是 .
17. (2015·南京中考)如图,过原点O的直线与反比例函数y1、y2的图象在第一象限内分别交于点A、B,且A为OB的中点,若函数y1=,则y2与x的函数表达式是________.
HYPERLINK "http://www.21cnjy.com"
第18题图
第17题图
18. (2015 浙江绍兴中考)在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(,).如图,若曲线与此正方形的边有交点,则的取值范围是___________.
三、解答题(共46分)
19.(5分)如图,正比例函数的图象与反比例函数
在第一象限内的图象交于点,过点作
轴的垂线,垂足为,已知△ 的面积为1.
(1)求反比例函数的解析式;
(2)如果为反比例函数在第一象限图象上的点(点与
点不重合),且点的横坐标为1,在轴上求一点,
使最小.
20.(6分)(浙江中考)若反比例函数与一次函数的图象都经过点A(a,2).
(1)求反比例函数的解析式;
(2) 当反比例函数的值大于一次函数的值时,
求自变量x的取值范围.
21.(5分)已知反比例函数(m为常数)的图象经过点A(-1,6).
(1)求m的值;
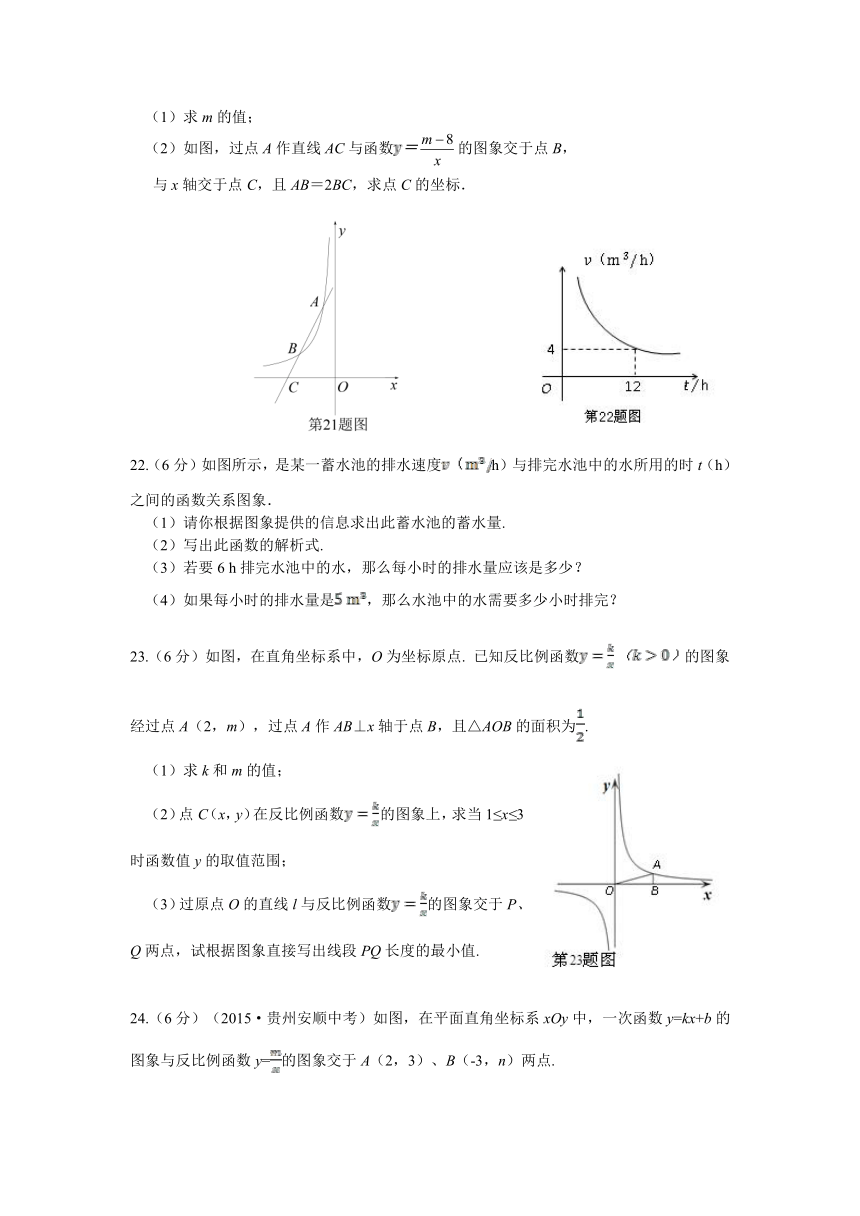
(2)如图,过点A作直线AC与函数的图象交于点B,
与x轴交于点C,且AB=2BC,求点C的坐标.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
22.(6分)如图所示,是某一蓄水池的排水速度h)与排完水池中的水所用的时t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的蓄水量.
(2)写出此函数的解析式.
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
(4)如果每小时的排水量是,那么水池中的水需要多少小时排完?
23.(6分)如图,在直角坐标系中,O为坐标原点. 已知反比例函数的图象
经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为.
(1)求k和m的值;
(2)点C(x,y)在反比例函数的图象上,求当1≤x≤3时函数值y的取值范围;
(3)过原点O的直线l与反比例函数的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
24.(6分)(2015·贵州安顺中考)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3)、B(-3,n)两点.
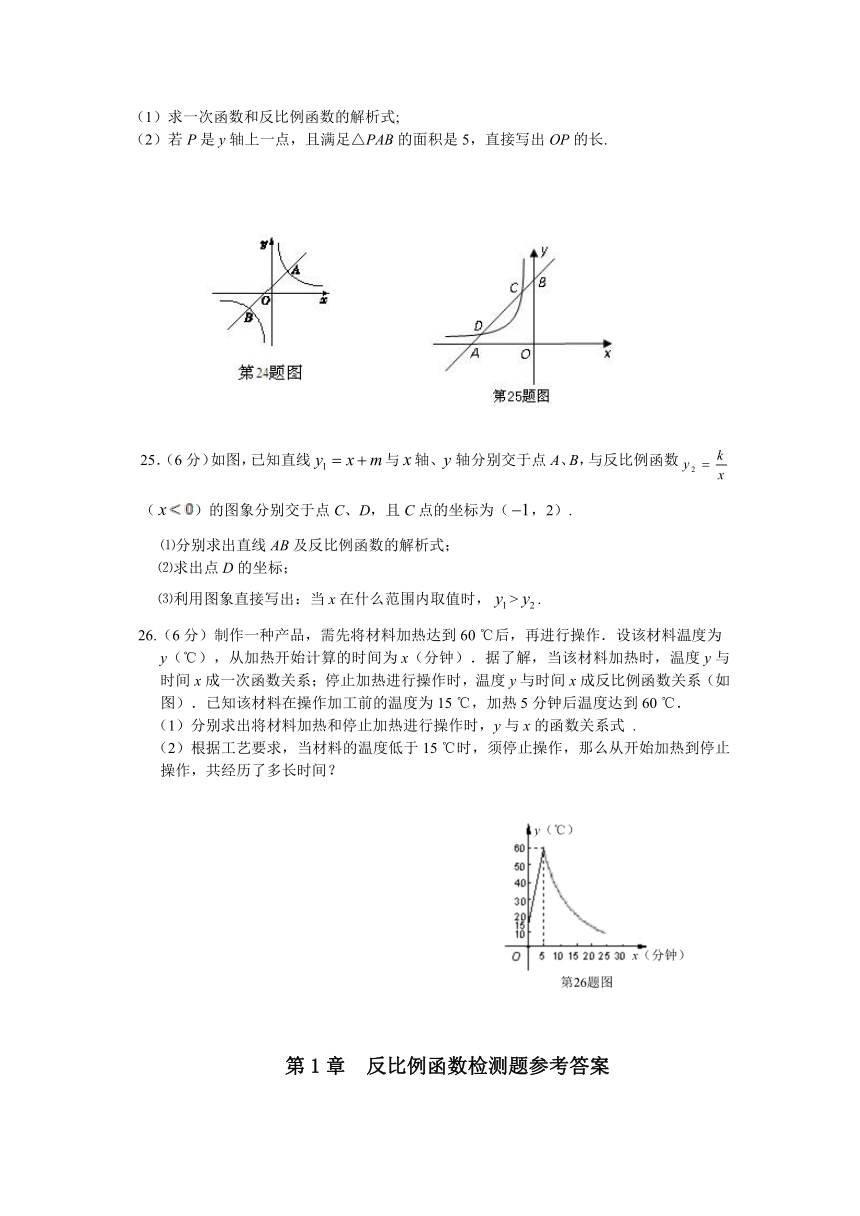
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,直接写出OP的长.
25.(6分)如图,已知直线与轴、轴分别交于点A、B,与反比例函数 ()的图象分别交于点C、D,且C点的坐标为(,2).
⑴分别求出直线AB及反比例函数的解析式;
⑵求出点D的坐标;
⑶利用图象直接写出:当x在什么范围内取值时,>.
26.(6分)制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为
y(℃),从加热开始计算的时间为x(分钟 ( http: / / www.21cnjy.com )).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例函数关系(如图).已知该材料在操作加工前的温度为15 ℃,加热5分钟后温度达到60 ℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式 .
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多长时间?
( http: / / www.21cnjy.com )
第1章 反比例函数检测题参考答案
1. C 解析:对于反比例函数y=,当x=1时,y=6,当x=3时,y=2,又因为在每个象限内y随x的增大而减小,所以2<y<6,故选C.
2.A 解析:因为函数的图象经过点(,,所以k=-1,所以y=kx-2=-x-2,根据一次函数的图象可知不经过第一象限.
3.A 解析:由于不知道k的符号,此题可以分类讨论,当时,反比例函数的图象在第一、三象限,一次函数的图象经过第一、二、三象限,可知A项符合;同理可讨论当时的情况.
4. D 解析:与的图象均为中心对称图形,则A、B两点关于原点对称,所以B点的横坐标为-2,观察图象发现:在y轴左侧,当-22时,正比例函数的图象上的点比反比例函数的图象上的点高.所以当 时,的取值范围是-22.
5.D 解析:由题意知
6.A 解析:因为反比例函数的图象位于第二、四象限,所以,即.又,所以或 (舍去).所以,故选A.
7. C 解析:如图,设点B的坐标为(x,y),过点B作轴于点C.在等边△ABO中,OC=,,即x=1,y=,所以点B(1,).又因为反比例函数y=的图象经过点B(1,),所以k=xy=.
8.D 解析:是反比例函数,且,
∴ 双曲线在第二、四象限,在各个象限内,y随x的增大而增大.
在第二象限,且,∴0<y1<y2.
又∵点(2,y3)在第四象限,∴y3<0.
因此y1,y2,y3的大小关系是y3<y1<y2,故选D.
9. C 解析:如图所示,作AH⊥y轴,垂足为点H,∵ 点A的坐标为(-3,4),∴ AH=3,OH=4.在Rt△AHO中,AO==5,∴ AB=AO=5.又∵ AB∥x轴,∴ 点B的坐标为(-8,4),把点B的坐标代入y=,得k=-32.
( http: / / www.21cnjy.com )
第9题答图
10. D 解析:如图,分别过点E,F作EG⊥OA,FH⊥OA,再过点E作
EM⊥FH并延长,交y轴于点N.过点F作FR⊥y轴于点R.
∵ 直线yx2分别与x轴,y轴的交点为A(2,0),B(0,2),
∴ △AOB为等腰直角三角形,AB=2.
∵ AB2EF,∴ EF=.
∵ △EMF为等腰直角三角形.∴ EM=FM=1. ∴ △AEG≌△BFR.
∵ S矩形EGON=S矩形FHOR=k,S△EMF=×1×1=,S△AOB=×2×2=2,
S矩形MHON=S△AEG+S△BFR,
∴ S矩形EGON +S矩形FHOR=S△AOB -S△EMF,即2k=2-=,解得k=.
11. y 解析:设反比例函数的解析式为y(k0),将点A(-2,-3)代入,得k=6,所以这个反比例函数的解析式为y=.
12. x≤-2或x>0
13. 解析:当反比例函数的图象在第一、三象限时,
14.4 解析:由反比例函数的图象位于第一、三象限内,得,即.又正比例函数的图象过第二、四象限,所以,所以.所以的整数值是4.
15. 反比例
16. 解析:若一次函数的图象与反比例函数的图象没有
公共点,则方程没有实数根,将方程整理得
1+4K<0 解得.
17. 解析:如图,过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,则,△AOC∽△BOD,
∴.
∵ 点A为OB的中点,
∴ ,∴ .
设y2与x的函数表达式是,则,∴ .
∵ 函数y2的图象在第一、三象限,∴ k>0,
∴ k=4, ∴ y2与x的函数表达式是.
18.-1≤a≤ 解析:点A的坐标为(a,a),且边长为1的正方形ABCD的边均平行于坐标轴,所以点B的坐标为(a+1,a)、点C的坐标为(a+1,a+1)、点D的坐标为(a,a+1).
因为曲线与正方形有交点,所以当曲线过点A时,,解得(不合题意,舍去);当曲线过点C时,,即,解得(不合题意,舍去),所以的取值范围是-1≤a≤.
19.解:(1) 设A点的坐标为(,),则.∴ .
∵ ,∴ .∴ .
∴ 反比例函数的解析式为.
(2) 由 得或 ∴ A为.
设A点关于轴的对称点为C,则C点的坐标为(2,-1).
若要在轴上求一点P,使PA+PB最小,则P点应为BC和
x轴的交点,如图所示.
令直线BC的解析式为.
∵ B为(,),∴解得
∴ BC的解析式为.
当时,,∴ P点坐标为(,).
20.解:(1)因为y=2x-4的图象过点所以.
因为的图象过点A(3,2),所以,所以.
(2) 求反比例函数与一次函数的图象的交点坐标,得到方程:
,解得x1= 3, x2=-1.
∴ 另外一个交点是(-1,-6).
画出图象,可知当或时,.
21.解:(1)因为图象过点A(-1,6),所以.所以.
(2)如图,分别过点A、B作x轴的垂线,垂足分别为点D、E,
由题意得,AD=6,OD=1,易知,AD∥BE,
∴ △CBE∽△CAD,∴ .
∵ AB=2BC,∴ ,∴ ,
∴ BE=2,即点B的纵坐标为2.
当y=2时,,易知:直线AB的解析式为y=2x+8,
∴ C (-4,0).
22.分析:观察图象易知:(1)蓄水池的蓄水量为48;
(2)与之间是反比例函数关系,所以可以设,依据图象上已知点(12,4)可以求得与之间的函数关系式;
(3)求当h时的值;
(4)求当h时t的值.
解:(1)蓄水池的蓄水量为12×4=48().
(2)函数的解析式为.
(3).
(4)依题意有,解得(h).
即如果每小时的排水量是5 ,那么水池中的水需要9.6 h排完.
23.解:(1)因为A(2,),所以,.
所以,所以.
所以点A的坐标为.
把A代入,得=,所以.
(2)因为当时,;当时,,
又反比例函数在时,随的增大而减小,
所以当时,的取值范围为.
(3)由图象可得,线段PQ长度的最小值为2.
24.解:(1)∵ 反比例函数y=的图象经过点A(2,3),
∴ m=6.∴ 反比例函数的解析式是y=.
∵ 点B(-3,n)在反比例函数y=的图象上,∴ n=-2.∴ B(-3,-2).
∵ 一次函数y=kx+b的图象经过A(2,3)、B(-3,-2)两点,
∴ 解得
∴ 一次函数的解析式是y=x+1.
(2)OP的长为3或1.
25.解:(1)将C点坐标(,2)代入,得,所以;
将C点坐标(,2)代入,得,所以.
(2)联立方程组解得
所以D点坐标为(-2,1).
(3)当>时,一次函数图象在反比例函数图象上方,
此时x的取值范围是.
26.解:(1)当时,为一次函数,
设一次函数解析式为,
由于一次函数图象过点(0,15),(5,60),
所以解得所以.
当时,为反比例函数,设函数关系式为,
由于图象过点(5,60),所以.
综上可知,y与x的函数关系式为
(2)当时,,
所以从开始加热到停止操作,共经历了20分钟.
y
x
O
A
O
y
x
B
O
y
x
C
O
x
y
D
C
B
P
第19题答图
(满分:100分,时间:90分钟)
一、选择题(每小题3分,共30分)
1. .( 2015·天津中考)已知反比例函数y=,当1
2.函数的图象经过点,则函数的图象不经过第( )象限.
A .一 B.二 C.三 D.四
3.在同一直角坐标系中,函数和的图象大致是( )
4. (2015·山东青岛中考)如图,正比例函数的图象与反比例函数的图象相交于A、B两点,其中点A的横坐标为2,当时,的取值范围是( )
A.x<-2或x>2 B.x<-2或0
5.购买只茶杯需15元,则购买茶杯的单价与的关系式为( )
A. (取实数) B. (取整数)
C. (取自然数) D. (取正整数)
6.若反比例函数的图象位于第二、四象限,则的值是( )
A. 0 B.0或1 C.0或2 D.4
7.(2015·浙江温州中考)如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限.若反比例函数的图象经过点B,则的值是( )
A. 1 B. 2 C. D.
8. 在函数(a为常数)的图象上有三点(-3,y1),(-1,y2),(2,y3),则函数值y1,y2,y3的大小关系是( )
A. B.
C. D.
9. (2015 江苏连云港中考)如图,O为坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=(x<0)的图象经过顶点B,则k的值为( )
A. -12 B. -27 C. -32 D. -36
10.(2014·福州中考) 如图,已知直线yx2分别与x轴、y轴交于A,B两点,与双曲线y交于E,F两点,若AB2EF,则k的值是( )
A.1 B.1 C. D.
二、填空题(每小题3分,共24分)
11. (2015·福州中考)一个反比例函数图象过点A(2,3),则这个反比例函数的解析式是________.
12. 若点在反比例函数的图象上,则当函数值时,自变量x的取值范围是___________.
13.已知反比例函数,当时,其图象的两个分支在第一、三象限内;当时,其图象在每个象限内随的增大而增大.
14.若反比例函数的图象位于第一、三象限内,正比例函数的图象过第二、四象限,则的整数值是________.
15.现有一批救灾物资要从A市运往B市,如果两市的距离为500千米,车速为每小时千米,从A市到B市所需时间为小时,那么与之间的函数关系式为_________,是的________ 函数.
16.(湖北黄石中考)若一次函数的图象与反比例函数的图象没有公共点,则实数k的取值范围是 .
17. (2015·南京中考)如图,过原点O的直线与反比例函数y1、y2的图象在第一象限内分别交于点A、B,且A为OB的中点,若函数y1=,则y2与x的函数表达式是________.
HYPERLINK "http://www.21cnjy.com"
第18题图
第17题图
18. (2015 浙江绍兴中考)在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(,).如图,若曲线与此正方形的边有交点,则的取值范围是___________.
三、解答题(共46分)
19.(5分)如图,正比例函数的图象与反比例函数
在第一象限内的图象交于点,过点作
轴的垂线,垂足为,已知△ 的面积为1.
(1)求反比例函数的解析式;
(2)如果为反比例函数在第一象限图象上的点(点与
点不重合),且点的横坐标为1,在轴上求一点,
使最小.
20.(6分)(浙江中考)若反比例函数与一次函数的图象都经过点A(a,2).
(1)求反比例函数的解析式;
(2) 当反比例函数的值大于一次函数的值时,
求自变量x的取值范围.
21.(5分)已知反比例函数(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线AC与函数的图象交于点B,
与x轴交于点C,且AB=2BC,求点C的坐标.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
22.(6分)如图所示,是某一蓄水池的排水速度h)与排完水池中的水所用的时t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的蓄水量.
(2)写出此函数的解析式.
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
(4)如果每小时的排水量是,那么水池中的水需要多少小时排完?
23.(6分)如图,在直角坐标系中,O为坐标原点. 已知反比例函数的图象
经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为.
(1)求k和m的值;
(2)点C(x,y)在反比例函数的图象上,求当1≤x≤3时函数值y的取值范围;
(3)过原点O的直线l与反比例函数的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
24.(6分)(2015·贵州安顺中考)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3)、B(-3,n)两点.
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,直接写出OP的长.
25.(6分)如图,已知直线与轴、轴分别交于点A、B,与反比例函数 ()的图象分别交于点C、D,且C点的坐标为(,2).
⑴分别求出直线AB及反比例函数的解析式;
⑵求出点D的坐标;
⑶利用图象直接写出:当x在什么范围内取值时,>.
26.(6分)制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为
y(℃),从加热开始计算的时间为x(分钟 ( http: / / www.21cnjy.com )).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例函数关系(如图).已知该材料在操作加工前的温度为15 ℃,加热5分钟后温度达到60 ℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式 .
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多长时间?
( http: / / www.21cnjy.com )
第1章 反比例函数检测题参考答案
1. C 解析:对于反比例函数y=,当x=1时,y=6,当x=3时,y=2,又因为在每个象限内y随x的增大而减小,所以2<y<6,故选C.
2.A 解析:因为函数的图象经过点(,,所以k=-1,所以y=kx-2=-x-2,根据一次函数的图象可知不经过第一象限.
3.A 解析:由于不知道k的符号,此题可以分类讨论,当时,反比例函数的图象在第一、三象限,一次函数的图象经过第一、二、三象限,可知A项符合;同理可讨论当时的情况.
4. D 解析:与的图象均为中心对称图形,则A、B两点关于原点对称,所以B点的横坐标为-2,观察图象发现:在y轴左侧,当-2
5.D 解析:由题意知
6.A 解析:因为反比例函数的图象位于第二、四象限,所以,即.又,所以或 (舍去).所以,故选A.
7. C 解析:如图,设点B的坐标为(x,y),过点B作轴于点C.在等边△ABO中,OC=,,即x=1,y=,所以点B(1,).又因为反比例函数y=的图象经过点B(1,),所以k=xy=.
8.D 解析:是反比例函数,且,
∴ 双曲线在第二、四象限,在各个象限内,y随x的增大而增大.
在第二象限,且,∴0<y1<y2.
又∵点(2,y3)在第四象限,∴y3<0.
因此y1,y2,y3的大小关系是y3<y1<y2,故选D.
9. C 解析:如图所示,作AH⊥y轴,垂足为点H,∵ 点A的坐标为(-3,4),∴ AH=3,OH=4.在Rt△AHO中,AO==5,∴ AB=AO=5.又∵ AB∥x轴,∴ 点B的坐标为(-8,4),把点B的坐标代入y=,得k=-32.
( http: / / www.21cnjy.com )
第9题答图
10. D 解析:如图,分别过点E,F作EG⊥OA,FH⊥OA,再过点E作
EM⊥FH并延长,交y轴于点N.过点F作FR⊥y轴于点R.
∵ 直线yx2分别与x轴,y轴的交点为A(2,0),B(0,2),
∴ △AOB为等腰直角三角形,AB=2.
∵ AB2EF,∴ EF=.
∵ △EMF为等腰直角三角形.∴ EM=FM=1. ∴ △AEG≌△BFR.
∵ S矩形EGON=S矩形FHOR=k,S△EMF=×1×1=,S△AOB=×2×2=2,
S矩形MHON=S△AEG+S△BFR,
∴ S矩形EGON +S矩形FHOR=S△AOB -S△EMF,即2k=2-=,解得k=.
11. y 解析:设反比例函数的解析式为y(k0),将点A(-2,-3)代入,得k=6,所以这个反比例函数的解析式为y=.
12. x≤-2或x>0
13. 解析:当反比例函数的图象在第一、三象限时,
14.4 解析:由反比例函数的图象位于第一、三象限内,得,即.又正比例函数的图象过第二、四象限,所以,所以.所以的整数值是4.
15. 反比例
16. 解析:若一次函数的图象与反比例函数的图象没有
公共点,则方程没有实数根,将方程整理得
1+4K<0 解得.
17. 解析:如图,过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,则,△AOC∽△BOD,
∴.
∵ 点A为OB的中点,
∴ ,∴ .
设y2与x的函数表达式是,则,∴ .
∵ 函数y2的图象在第一、三象限,∴ k>0,
∴ k=4, ∴ y2与x的函数表达式是.
18.-1≤a≤ 解析:点A的坐标为(a,a),且边长为1的正方形ABCD的边均平行于坐标轴,所以点B的坐标为(a+1,a)、点C的坐标为(a+1,a+1)、点D的坐标为(a,a+1).
因为曲线与正方形有交点,所以当曲线过点A时,,解得(不合题意,舍去);当曲线过点C时,,即,解得(不合题意,舍去),所以的取值范围是-1≤a≤.
19.解:(1) 设A点的坐标为(,),则.∴ .
∵ ,∴ .∴ .
∴ 反比例函数的解析式为.
(2) 由 得或 ∴ A为.
设A点关于轴的对称点为C,则C点的坐标为(2,-1).
若要在轴上求一点P,使PA+PB最小,则P点应为BC和
x轴的交点,如图所示.
令直线BC的解析式为.
∵ B为(,),∴解得
∴ BC的解析式为.
当时,,∴ P点坐标为(,).
20.解:(1)因为y=2x-4的图象过点所以.
因为的图象过点A(3,2),所以,所以.
(2) 求反比例函数与一次函数的图象的交点坐标,得到方程:
,解得x1= 3, x2=-1.
∴ 另外一个交点是(-1,-6).
画出图象,可知当或时,.
21.解:(1)因为图象过点A(-1,6),所以.所以.
(2)如图,分别过点A、B作x轴的垂线,垂足分别为点D、E,
由题意得,AD=6,OD=1,易知,AD∥BE,
∴ △CBE∽△CAD,∴ .
∵ AB=2BC,∴ ,∴ ,
∴ BE=2,即点B的纵坐标为2.
当y=2时,,易知:直线AB的解析式为y=2x+8,
∴ C (-4,0).
22.分析:观察图象易知:(1)蓄水池的蓄水量为48;
(2)与之间是反比例函数关系,所以可以设,依据图象上已知点(12,4)可以求得与之间的函数关系式;
(3)求当h时的值;
(4)求当h时t的值.
解:(1)蓄水池的蓄水量为12×4=48().
(2)函数的解析式为.
(3).
(4)依题意有,解得(h).
即如果每小时的排水量是5 ,那么水池中的水需要9.6 h排完.
23.解:(1)因为A(2,),所以,.
所以,所以.
所以点A的坐标为.
把A代入,得=,所以.
(2)因为当时,;当时,,
又反比例函数在时,随的增大而减小,
所以当时,的取值范围为.
(3)由图象可得,线段PQ长度的最小值为2.
24.解:(1)∵ 反比例函数y=的图象经过点A(2,3),
∴ m=6.∴ 反比例函数的解析式是y=.
∵ 点B(-3,n)在反比例函数y=的图象上,∴ n=-2.∴ B(-3,-2).
∵ 一次函数y=kx+b的图象经过A(2,3)、B(-3,-2)两点,
∴ 解得
∴ 一次函数的解析式是y=x+1.
(2)OP的长为3或1.
25.解:(1)将C点坐标(,2)代入,得,所以;
将C点坐标(,2)代入,得,所以.
(2)联立方程组解得
所以D点坐标为(-2,1).
(3)当>时,一次函数图象在反比例函数图象上方,
此时x的取值范围是.
26.解:(1)当时,为一次函数,
设一次函数解析式为,
由于一次函数图象过点(0,15),(5,60),
所以解得所以.
当时,为反比例函数,设函数关系式为,
由于图象过点(5,60),所以.
综上可知,y与x的函数关系式为
(2)当时,,
所以从开始加热到停止操作,共经历了20分钟.
y
x
O
A
O
y
x
B
O
y
x
C
O
x
y
D
C
B
P
第19题答图
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
