2024年中考数学高频考点常见题型突破——实际问题与二次函数(含答案)
文档属性
| 名称 | 2024年中考数学高频考点常见题型突破——实际问题与二次函数(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 18:51:22 | ||
图片预览


文档简介
2024年中考数学高频考点常见题型突破——
实际问题与二次函数
一、解答题
1.某果园有棵橙子树,平均每棵树结个橙子.现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结个橙子.假设果园增种棵橙子树,增种后果园橙子的总产量为个,那么请你求出当果园增种多少棵橙子树时,橙子的总产量最多,并求出此时的总产量.
2.普洱茶是中国十大名茶之一,也是中华古老文明中的一颗瑰宝.某公司经销某种品牌普洱茶,每千克成本为50元.经市场调查发现:每周销售量y(千克)与销售单价x(元/千克)满足一次函数关系,部分数据如下表所示,
销售单价x(元/千克) 56 65 75
销售量y(千克) 128 110 90
解答下列问题:
(1)求y与x的函数关系式;
(2)求这一周销售这种品牌普洱茶获得的利润W元的最大值;
(3)物价部门规定茶叶销售单价不得高于90元/千克,公司想获得不低于2000元周利润,请计算销售单价范围.
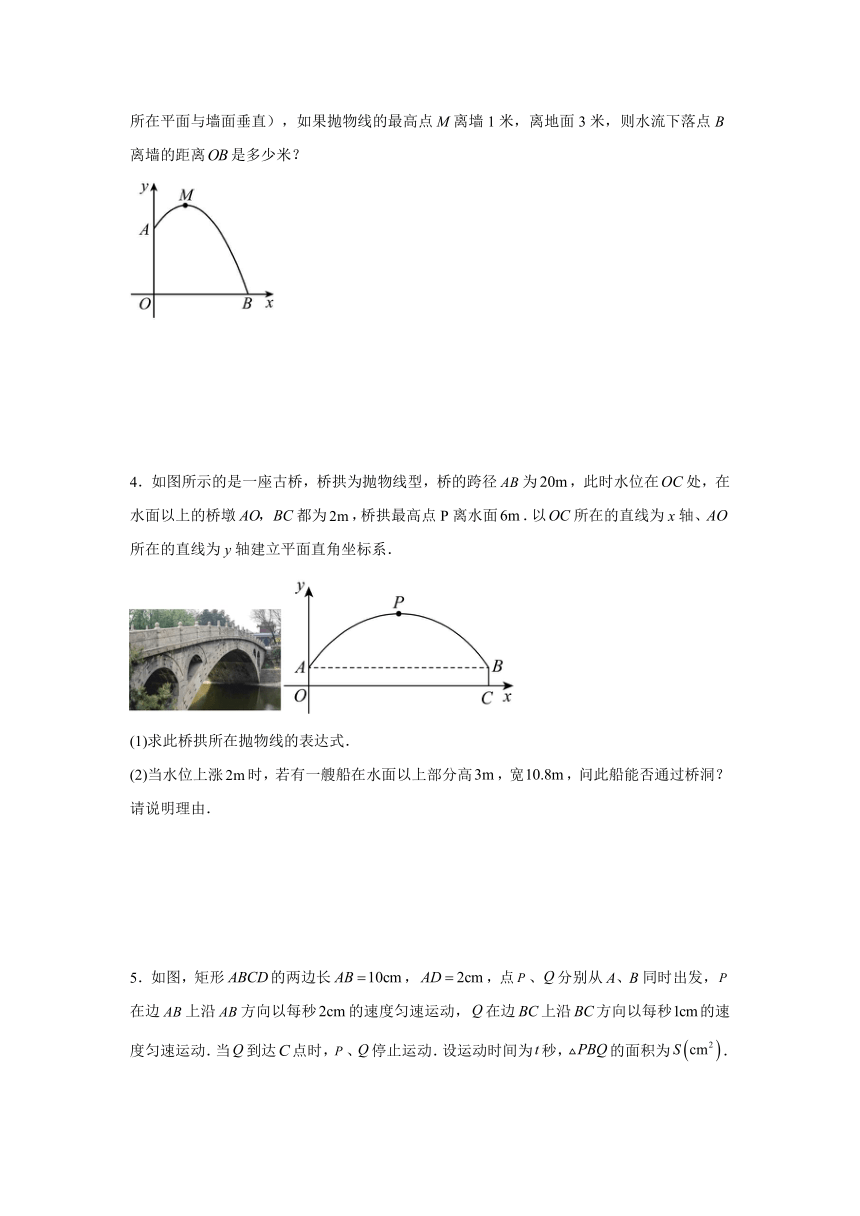
3.如图,某幢建筑物从米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离是多少米?
4.如图所示的是一座古桥,桥拱为抛物线型,桥的跨径为,此时水位在处,在水面以上的桥墩都为,桥拱最高点P离水面.以所在的直线为x轴、所在的直线为y轴建立平面直角坐标系.
(1)求此桥拱所在抛物线的表达式.
(2)当水位上涨时,若有一艘船在水面以上部分高,宽,问此船能否通过桥洞?请说明理由.
5.如图,矩形的两边长,,点、分别从A、B同时出发,在边上沿方向以每秒的速度匀速运动,在边上沿方向以每秒的速度匀速运动.当到达点时,、停止运动.设运动时间为秒,的面积为.
(1)填空: , (用含的代数式表示);
(2)求关于的函数关系式,并写出的取值范围;
(3)当为何值时,的面积的最大,最大值是多少?
6.音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化,某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边,音乐变化时,抛物线的顶点在直线上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为.
(1)若已知,且喷出的抛物线水线最大高度达,求此时a、b的值;
(2)若,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若,且要求喷出的抛物线水线不能到岸边,求a的取值范围.
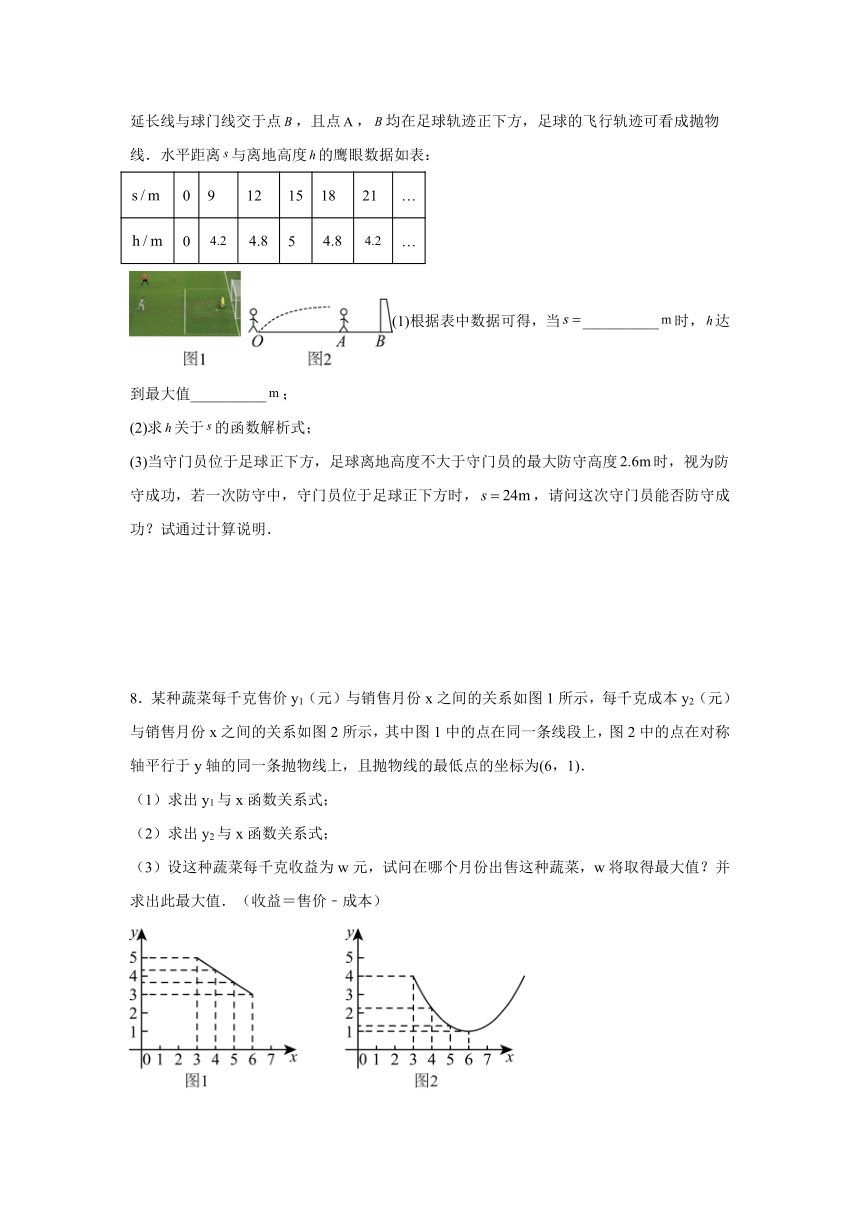
7.鹰眼技术助力杭州亚运,提升球迷观赛体验.如图分别为足球比赛中某一时刻的鹰眼系统预测画面(如图1)和截面示意图(如图2),攻球员位于点,守门员位于点,的延长线与球门线交于点,且点,均在足球轨迹正下方,足球的飞行轨迹可看成抛物线.水平距离与离地高度的鹰眼数据如表:
0 9 12 15 18 21 …
0 5 …
(1)根据表中数据可得,当__________时,达到最大值__________;
(2)求关于的函数解析式;
(3)当守门员位于足球正下方,足球离地高度不大于守门员的最大防守高度时,视为防守成功,若一次防守中,守门员位于足球正下方时,,请问这次守门员能否防守成功?试通过计算说明.
8.某种蔬菜每千克售价y1(元)与销售月份x之间的关系如图1所示,每千克成本y2(元)与销售月份x之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在对称轴平行于y轴的同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出y1与x函数关系式;
(2)求出y2与x函数关系式;
(3)设这种蔬菜每千克收益为w元,试问在哪个月份出售这种蔬菜,w将取得最大值?并求出此最大值.(收益=售价﹣成本)
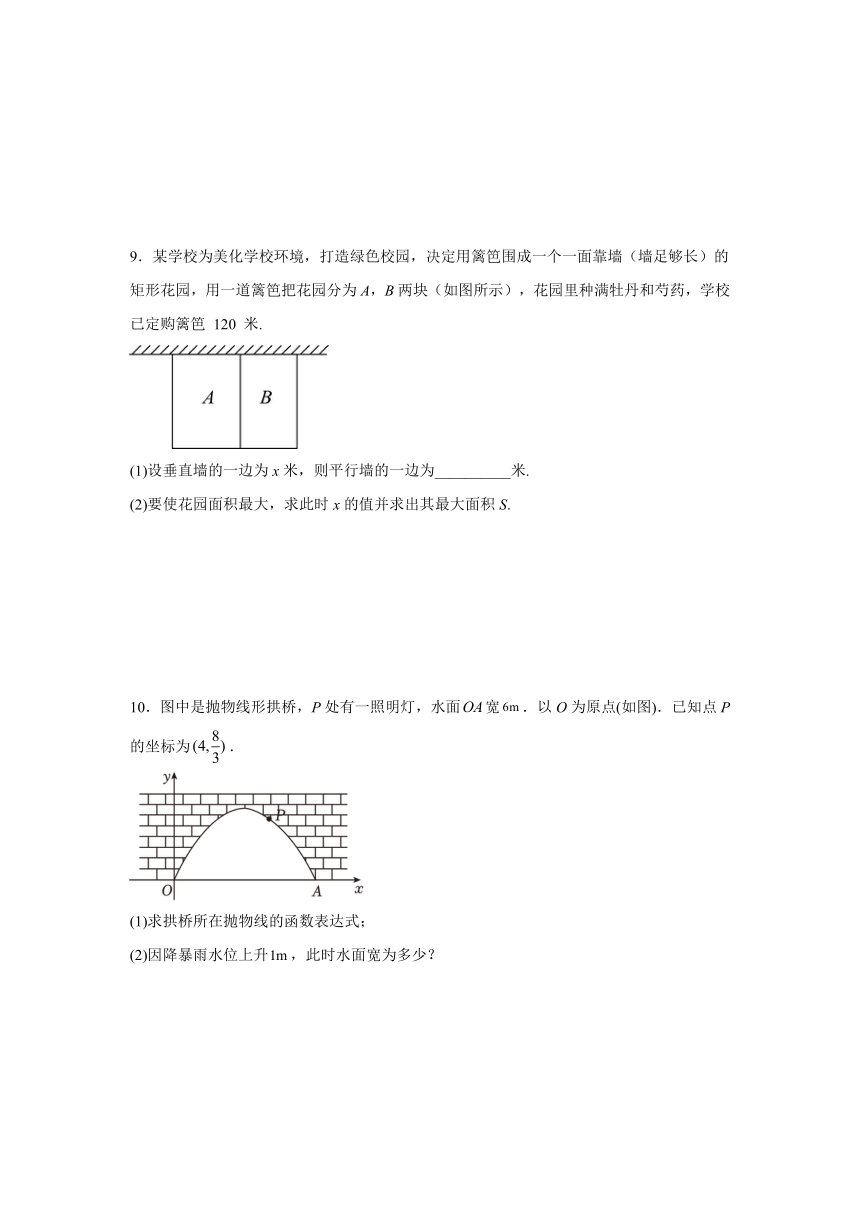
9.某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为A,B两块(如图所示),花园里种满牡丹和芍药,学校已定购篱笆 120 米.
(1)设垂直墙的一边为x米,则平行墙的一边为__________米.
(2)要使花园面积最大,求此时x的值并求出其最大面积S.
10.图中是抛物线形拱桥,P处有一照明灯,水面宽.以O为原点(如图).已知点P的坐标为.
(1)求拱桥所在抛物线的函数表达式;
(2)因降暴雨水位上升,此时水面宽为多少?
11.某商店购进了一种消毒用品,进价为每件元,在销售过程中发现,每天的销售量件与每件售价(元)之间存在一次函数关系(其中,且为整数).当每件消毒用品售价为元时,每天的销售量为件;当每件消毒用品售价为元时,每天的销售量为件.
(1)求与之间的函数关系式;
(2)若该商店销售这种消毒用品每天获得元的利润,则每件消毒用品的售价为多少元
(3)设该商店销售这种消毒用品每天获利(元),当每件消毒用品的售价为多少元时每天的销售利润最大 最大利润是多少元
12.图①是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据《范蠡兵法》记载:“飞石重十二斤,为机发,行二百步”,其原理蕴含了物理中的“杠杆原理”.
在如图②所示的平面直角坐标系中,将投石机置于斜坡的底部点处,石块从投石机竖直方向上的点处被投出,在斜坡上的点处建有垂直于水平面的城墙.已知,石块运动轨迹所在抛物线的顶点坐标是,,,,.
(1)求抛物线的解析式;
(2)通过计算说明石块能否飞越城墙;
(3)求出石块与斜坡在竖直方向上的最大距离.
13.如图,排球运动场的场地长,球网高度,球网在场地中央,距离球场左、右边界均为.一名球员在场地左侧边界练习发球,排球的飞行路线可以看作是对称轴垂直于水平面的抛物线的一部分.某次发球,排球从左边界的正上方发出,击球点的高度为,当排球飞行到距离球网时达到最大高度.小洛在下图中建立了平面直角坐标系,求得该抛物线的表达式为.
根据以上信息,解答下列问题:
(1)请在图中画出小洛建立的平而直角坐标系;
(2)判断排球能否过球网,并说明理由;
(3)判断排球是否会出界,并说明理由.
14.一座拱桥的示意图如图所示,当水面宽为米时,桥洞顶部离水面米.已知桥洞的拱桥是抛物线,请尝试解决以下问题:
(1)【问题1】建立合适的平面直角坐标系,求该抛物线的表达式.
(2)【问题2】由于暴雨导致水位上涨了米,求此时水面的宽度.
(3)【问题3】已知一艘货船的高为米,宽为米,其截面如图所示.为保证这艘货船可以安全通过拱桥,水面在正常水位的基础上最多能上升多少米?
15.如图1,劳动课同学们利用喷水头喷出的水对草坪进行喷灌作业以养护草坪.如图2,点处有一个喷水头,距离 水头的处有一棵高度是的树.距离这棵树的处有一面高的围墙.建立如图所示平面直角坐标系.已知喷水头喷出的水柱的竖直高度与水平距离近似满足函数关系.
(1)某次喷水浇灌时,测得与的几组数据如下:
0 2 6 10 12
0
①根据上述数据,求满足的函数关系;
②求喷水头喷出的水柱的最大高度;
(2)又一次喷水浇灌时,已知喷水头写出的水柱的竖直高度与水平距离近似满足函数关系.假设喷水头喷出的水柱能够越过这棵树,且不会浇到墙外,直接写出同时满足这两个要求的常数的范围.
16.如图,用一段长为的篱笆围成一个一边靠墙的矩形花圃,墙长.设长为,矩形的面积为.
(1)写出y与x的函数关系式;
(2)当花圃的面积为时,长为多少米?
(3)当长为多少米时,所围成的花團面积最大?最大值是多少?
17.某校在基地参加社会实践活动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的面积最大?有两位学生对此产生了争议.请根据信息,解决问题:
(1)设米,试用含x的代数式表示的长;
(2)请你判断谁的说法正确,为什么?
参考答案:
1.当果园增种棵橙子树时,橙子的总产量最多,此时的总产量为个
2.(1);(2)2450元;(3)
3.3米
4.(1)抛物线解析式为
(2)此船不能通过桥洞
5.(1),
(2);
(3)的最大面积是.
6.(1),
(2)9米
(3)
7.(1),
(2)
(3)守门员不能成功防守
8.(1)y1=﹣x+7;(2)y2=(x﹣6)2+1;(3)5月出售这种蔬菜,每千克收益最大,最大值
9.(1)
(2)当时,最大面积S为1200平方米
10.(1)
(2)
11.(1)
(2)元
(3)15元,525元
12.(1)
(2)石块不能飞越防御墙
(3)石块与斜坡在竖直方向上的最大距离为米
13.排球能过球网
排球会出界
14.(1)
(2)米
(3)米
15.(1)①;②喷水头喷出的水柱的最大高度为
(2)
16.(1)
(2)当长为时,面积为
(3)当长为时,花圃面积最大,最大面积为
17.(1)
(2)小英说法正确
实际问题与二次函数
一、解答题
1.某果园有棵橙子树,平均每棵树结个橙子.现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结个橙子.假设果园增种棵橙子树,增种后果园橙子的总产量为个,那么请你求出当果园增种多少棵橙子树时,橙子的总产量最多,并求出此时的总产量.
2.普洱茶是中国十大名茶之一,也是中华古老文明中的一颗瑰宝.某公司经销某种品牌普洱茶,每千克成本为50元.经市场调查发现:每周销售量y(千克)与销售单价x(元/千克)满足一次函数关系,部分数据如下表所示,
销售单价x(元/千克) 56 65 75
销售量y(千克) 128 110 90
解答下列问题:
(1)求y与x的函数关系式;
(2)求这一周销售这种品牌普洱茶获得的利润W元的最大值;
(3)物价部门规定茶叶销售单价不得高于90元/千克,公司想获得不低于2000元周利润,请计算销售单价范围.
3.如图,某幢建筑物从米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离是多少米?
4.如图所示的是一座古桥,桥拱为抛物线型,桥的跨径为,此时水位在处,在水面以上的桥墩都为,桥拱最高点P离水面.以所在的直线为x轴、所在的直线为y轴建立平面直角坐标系.
(1)求此桥拱所在抛物线的表达式.
(2)当水位上涨时,若有一艘船在水面以上部分高,宽,问此船能否通过桥洞?请说明理由.
5.如图,矩形的两边长,,点、分别从A、B同时出发,在边上沿方向以每秒的速度匀速运动,在边上沿方向以每秒的速度匀速运动.当到达点时,、停止运动.设运动时间为秒,的面积为.
(1)填空: , (用含的代数式表示);
(2)求关于的函数关系式,并写出的取值范围;
(3)当为何值时,的面积的最大,最大值是多少?
6.音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化,某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边,音乐变化时,抛物线的顶点在直线上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为.
(1)若已知,且喷出的抛物线水线最大高度达,求此时a、b的值;
(2)若,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若,且要求喷出的抛物线水线不能到岸边,求a的取值范围.
7.鹰眼技术助力杭州亚运,提升球迷观赛体验.如图分别为足球比赛中某一时刻的鹰眼系统预测画面(如图1)和截面示意图(如图2),攻球员位于点,守门员位于点,的延长线与球门线交于点,且点,均在足球轨迹正下方,足球的飞行轨迹可看成抛物线.水平距离与离地高度的鹰眼数据如表:
0 9 12 15 18 21 …
0 5 …
(1)根据表中数据可得,当__________时,达到最大值__________;
(2)求关于的函数解析式;
(3)当守门员位于足球正下方,足球离地高度不大于守门员的最大防守高度时,视为防守成功,若一次防守中,守门员位于足球正下方时,,请问这次守门员能否防守成功?试通过计算说明.
8.某种蔬菜每千克售价y1(元)与销售月份x之间的关系如图1所示,每千克成本y2(元)与销售月份x之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在对称轴平行于y轴的同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出y1与x函数关系式;
(2)求出y2与x函数关系式;
(3)设这种蔬菜每千克收益为w元,试问在哪个月份出售这种蔬菜,w将取得最大值?并求出此最大值.(收益=售价﹣成本)
9.某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为A,B两块(如图所示),花园里种满牡丹和芍药,学校已定购篱笆 120 米.
(1)设垂直墙的一边为x米,则平行墙的一边为__________米.
(2)要使花园面积最大,求此时x的值并求出其最大面积S.
10.图中是抛物线形拱桥,P处有一照明灯,水面宽.以O为原点(如图).已知点P的坐标为.
(1)求拱桥所在抛物线的函数表达式;
(2)因降暴雨水位上升,此时水面宽为多少?
11.某商店购进了一种消毒用品,进价为每件元,在销售过程中发现,每天的销售量件与每件售价(元)之间存在一次函数关系(其中,且为整数).当每件消毒用品售价为元时,每天的销售量为件;当每件消毒用品售价为元时,每天的销售量为件.
(1)求与之间的函数关系式;
(2)若该商店销售这种消毒用品每天获得元的利润,则每件消毒用品的售价为多少元
(3)设该商店销售这种消毒用品每天获利(元),当每件消毒用品的售价为多少元时每天的销售利润最大 最大利润是多少元
12.图①是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据《范蠡兵法》记载:“飞石重十二斤,为机发,行二百步”,其原理蕴含了物理中的“杠杆原理”.
在如图②所示的平面直角坐标系中,将投石机置于斜坡的底部点处,石块从投石机竖直方向上的点处被投出,在斜坡上的点处建有垂直于水平面的城墙.已知,石块运动轨迹所在抛物线的顶点坐标是,,,,.
(1)求抛物线的解析式;
(2)通过计算说明石块能否飞越城墙;
(3)求出石块与斜坡在竖直方向上的最大距离.
13.如图,排球运动场的场地长,球网高度,球网在场地中央,距离球场左、右边界均为.一名球员在场地左侧边界练习发球,排球的飞行路线可以看作是对称轴垂直于水平面的抛物线的一部分.某次发球,排球从左边界的正上方发出,击球点的高度为,当排球飞行到距离球网时达到最大高度.小洛在下图中建立了平面直角坐标系,求得该抛物线的表达式为.
根据以上信息,解答下列问题:
(1)请在图中画出小洛建立的平而直角坐标系;
(2)判断排球能否过球网,并说明理由;
(3)判断排球是否会出界,并说明理由.
14.一座拱桥的示意图如图所示,当水面宽为米时,桥洞顶部离水面米.已知桥洞的拱桥是抛物线,请尝试解决以下问题:
(1)【问题1】建立合适的平面直角坐标系,求该抛物线的表达式.
(2)【问题2】由于暴雨导致水位上涨了米,求此时水面的宽度.
(3)【问题3】已知一艘货船的高为米,宽为米,其截面如图所示.为保证这艘货船可以安全通过拱桥,水面在正常水位的基础上最多能上升多少米?
15.如图1,劳动课同学们利用喷水头喷出的水对草坪进行喷灌作业以养护草坪.如图2,点处有一个喷水头,距离 水头的处有一棵高度是的树.距离这棵树的处有一面高的围墙.建立如图所示平面直角坐标系.已知喷水头喷出的水柱的竖直高度与水平距离近似满足函数关系.
(1)某次喷水浇灌时,测得与的几组数据如下:
0 2 6 10 12
0
①根据上述数据,求满足的函数关系;
②求喷水头喷出的水柱的最大高度;
(2)又一次喷水浇灌时,已知喷水头写出的水柱的竖直高度与水平距离近似满足函数关系.假设喷水头喷出的水柱能够越过这棵树,且不会浇到墙外,直接写出同时满足这两个要求的常数的范围.
16.如图,用一段长为的篱笆围成一个一边靠墙的矩形花圃,墙长.设长为,矩形的面积为.
(1)写出y与x的函数关系式;
(2)当花圃的面积为时,长为多少米?
(3)当长为多少米时,所围成的花團面积最大?最大值是多少?
17.某校在基地参加社会实践活动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的面积最大?有两位学生对此产生了争议.请根据信息,解决问题:
(1)设米,试用含x的代数式表示的长;
(2)请你判断谁的说法正确,为什么?
参考答案:
1.当果园增种棵橙子树时,橙子的总产量最多,此时的总产量为个
2.(1);(2)2450元;(3)
3.3米
4.(1)抛物线解析式为
(2)此船不能通过桥洞
5.(1),
(2);
(3)的最大面积是.
6.(1),
(2)9米
(3)
7.(1),
(2)
(3)守门员不能成功防守
8.(1)y1=﹣x+7;(2)y2=(x﹣6)2+1;(3)5月出售这种蔬菜,每千克收益最大,最大值
9.(1)
(2)当时,最大面积S为1200平方米
10.(1)
(2)
11.(1)
(2)元
(3)15元,525元
12.(1)
(2)石块不能飞越防御墙
(3)石块与斜坡在竖直方向上的最大距离为米
13.排球能过球网
排球会出界
14.(1)
(2)米
(3)米
15.(1)①;②喷水头喷出的水柱的最大高度为
(2)
16.(1)
(2)当长为时,面积为
(3)当长为时,花圃面积最大,最大面积为
17.(1)
(2)小英说法正确
同课章节目录
