2023-2024学年人教版七年级上册数学期末专题训练:动角问题压轴题(含答案)
文档属性
| 名称 | 2023-2024学年人教版七年级上册数学期末专题训练:动角问题压轴题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 952.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 18:54:47 | ||
图片预览


文档简介
2023-2024学年人教版七年级上册数学期末专题训练:
动角问题压轴题
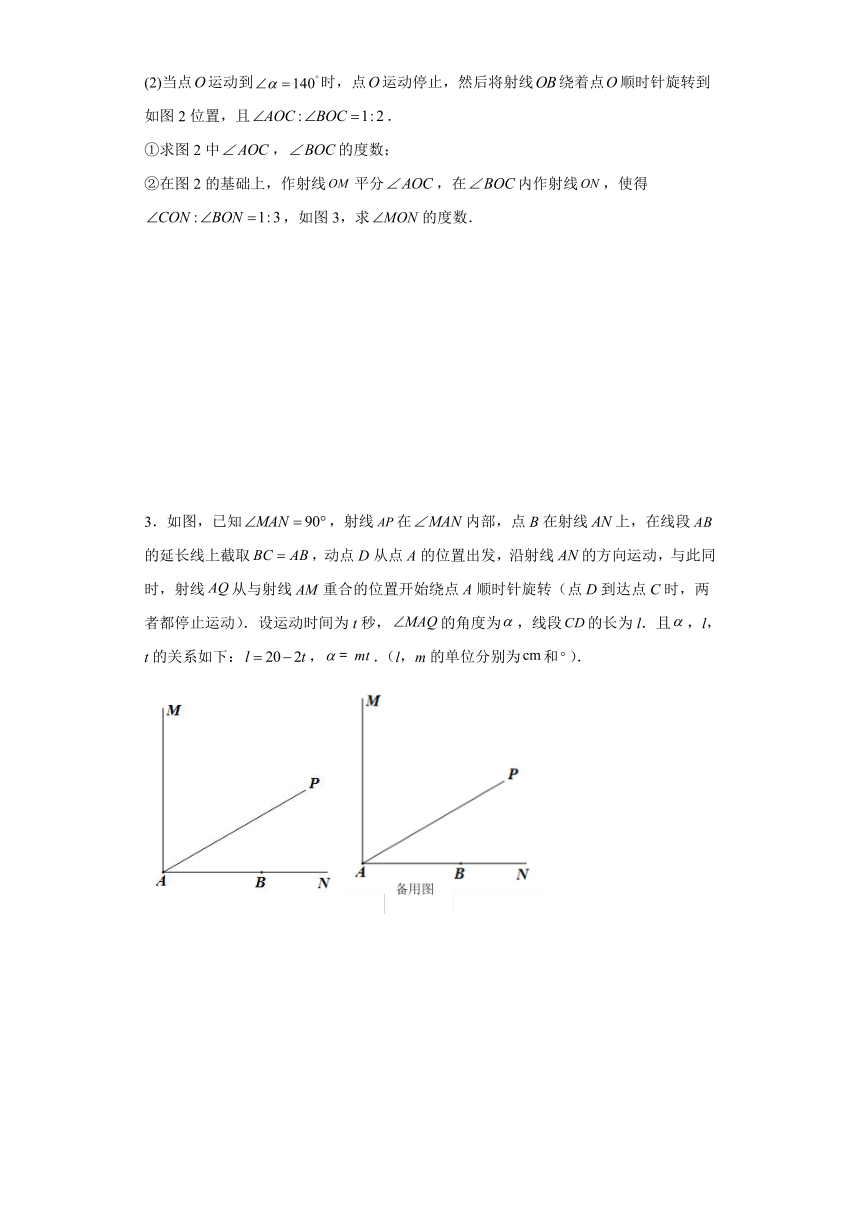
1.将一副三角板按图1摆放在直线上,平分,平分.
(1) ; ;
(2)如图2,若将三角板绕点以秒的速度顺时针旋转秒,求的度数;
(3)如图3,三角板绕点以秒的速度顺时针旋转,同时,三角板绕点以秒的速度逆时针旋转,当与边首次重合时两三角板都停止运动,若运行秒时,有成立,试求此时与的关系.
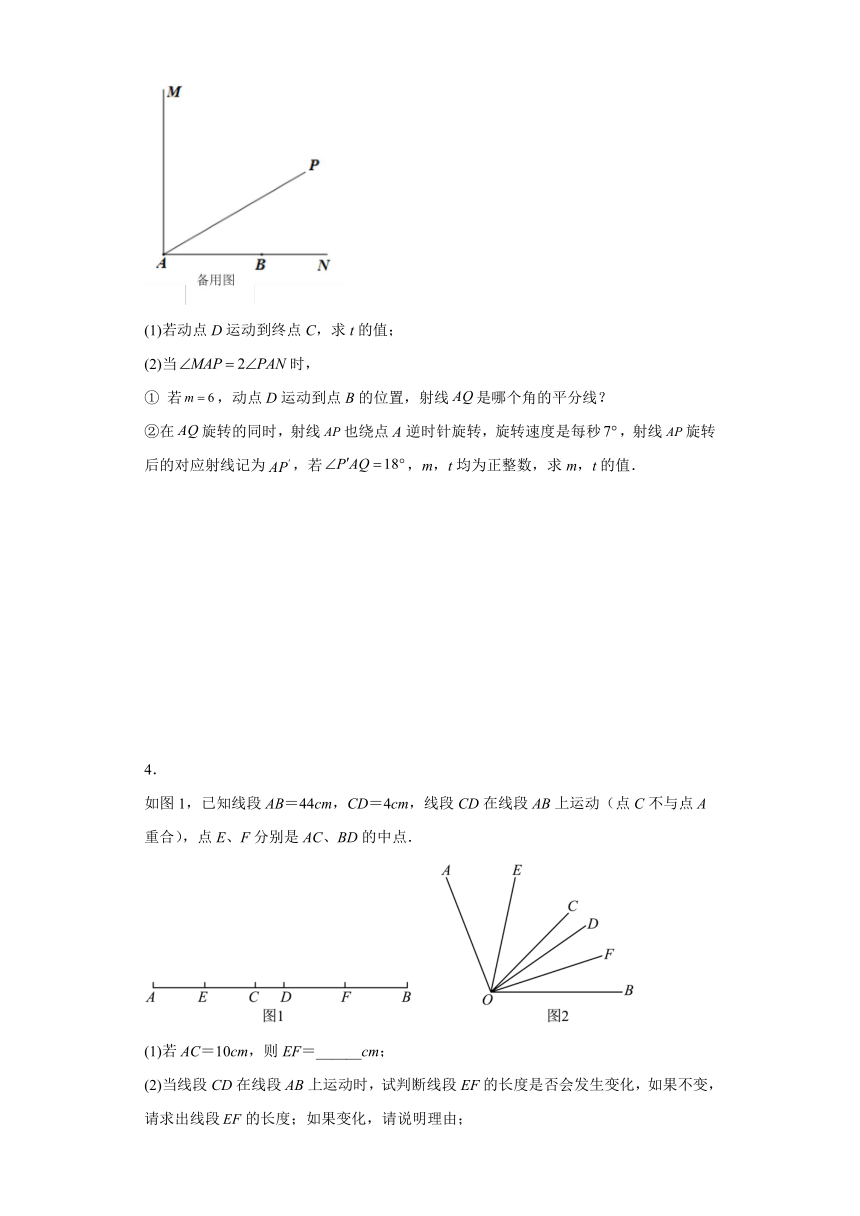
2.直线外有一定点,是直线上的一个动点.
(1)如图1所示,当点从左向右运动时,观察的变化情况,正确的是________
A.逐渐变大 B.逐渐变小 C.大小不变 D.无法确定
(2)当点运动到时,点运动停止,然后将射线绕着点顺时针旋转到如图2位置,且.
①求图2中,的度数;
②在图2的基础上,作射线平分,在内作射线,使得,如图3,求的度数.
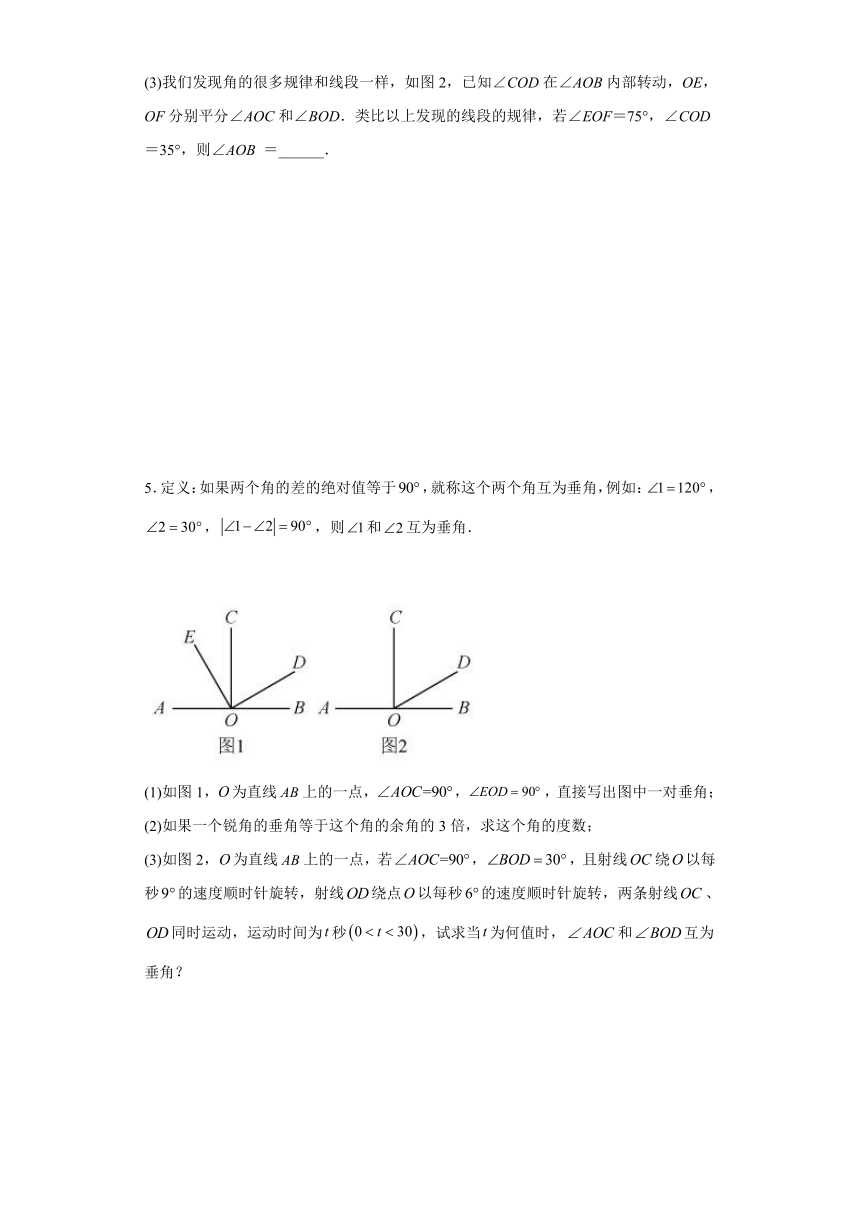
3.如图,已知,射线在内部,点B在射线上,在线段的延长线上截取,动点D从点A的位置出发,沿射线的方向运动,与此同时,射线从与射线重合的位置开始绕点A顺时针旋转(点D到达点C时,两者都停止运动).设运动时间为t秒,的角度为,线段的长为l.且,l,t的关系如下:,.(l,m的单位分别为和).
(1)若动点D运动到终点C,求t的值;
(2)当时,
① 若,动点D运动到点B的位置,射线是哪个角的平分线?
②在旋转的同时,射线也绕点A逆时针旋转,旋转速度是每秒,射线旋转后的对应射线记为,若,m,t均为正整数,求m,t的值.
4.
如图1,已知线段AB=44cm,CD=4cm,线段CD在线段AB上运动(点C不与点A重合),点E、F分别是AC、BD的中点.
(1)若AC=10cm,则EF=______cm;
(2)当线段CD在线段AB上运动时,试判断线段EF的长度是否会发生变化,如果不变,请求出线段的长度;如果变化,请说明理由;
(3)我们发现角的很多规律和线段一样,如图2,已知∠COD在∠AOB内部转动,OE,OF分别平分∠AOC和∠BOD.类比以上发现的线段的规律,若∠EOF=75°,∠COD=35°,则∠AOB =______.
5.定义:如果两个角的差的绝对值等于,就称这个两个角互为垂角,例如:,,,则和互为垂角.
(1)如图1,为直线上的一点,,,直接写出图中一对垂角;
(2)如果一个锐角的垂角等于这个角的余角的3倍,求这个角的度数;
(3)如图2,为直线上的一点,若,,且射线绕以每秒的速度顺时针旋转,射线绕点以每秒的速度顺时针旋转,两条射线、同时运动,运动时间为秒,试求当为何值时,和互为垂角?
6.如图①,已知线段在线段上运动,线段,,点、分别是、的中点.解答下列问题:
(1)若,求的长;
(2)当线段在线段上运动时,试判断的长度是否发生变化?如果不变请求出的长度,如果变化,请说明理由;
(3)通过类比,我们发现角的很多规律和线段一样,如图②已知在内部转动,和分别平分和,则与、有何数量关系,请直接写出答案.
7.【阅读理解】射线是内部的一条射线,若,则我们称射线是射线的“友好线”,例如,如图1,,,则,称射线是射线的友好线:同时,由于,称射线是射线的友好线.
(1)如图2,,射线是射线的友好线,则________;
(2)如图3,,射线与射线重合,并绕点以每秒的速度逆时针旋转,射线与射线重合,并绕点以每秒3゜的速度顺时针旋转,当射线与射线重合时,运动停止;
①是否存在某个时刻(秒),使得的度数是,若存在,求出的值,若不存在,请说明理由;
②当为多少秒时,射线、、中恰好有一条射线是另一条射线的友好线.(直接写出答案)
8.如图①,已知线段AB=20cm,CD=2cm,线段CD在线段AB上运动,E、F分别是AC、BD的中点.
(1)若AC=4cm,则EF=_________cm.
(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变请求出EF的长度,如果变化,请说明理由.
(3)我们发现角的很多规律和线段一样,如图②已知在内部转动,OE、OF分别平分在,则、和有何关系,请直接写出_______________________.
9.如图1,已知∠AOB=90°,∠COD=60°,射线OC,OB重合.
(1)∠AOD= ;
(2)如图2,若射线OB以每秒15°的速度绕点O逆时针旋转,同时若射线OC以每秒10°的速度绕点O顺时针旋转,当射线OB与OA重合时,两射线都停止运动,设旋转的时间为t秒,
①当∠BOC=90°时,求t的值;
②如图3,当有一条射线恰好是另外两条射线夹角的角平分线时,直接写出∠BOC的度数 (用t的代数式表示),并求t的值.
10.如图1,正方形和长方形的周长相等,且各有一条边在数轴上,点对应的数分别是.正方形以每秒2个单位长度的速度向右移动,同时长方形以每秒1个单位长度的速度向左移动.设正方形和长方形重叠部分的面积为S,移动时间为t.
(1)长方形的面积是______.
(2)当S是长方形面积的一半时,求t的值.
(3)如图2,当正方形和长方形运动到点B和点F重合时,停止运动,将正方形绕点B顺时针旋转,旋转角度为,点分别在线段、线段的延长线上,平分,判断和之间的数量关系,用等式表示,并说明理由.
11.如图1,点O为直线上一点,过点O作射线,使,将一直角三角板的直角顶点放在点O处(),一边在射线上,另一边在直线的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边在的内部,且恰好平分.求的度数.
(2)将图1中三角板绕点O以每秒的速度沿逆时针方向旋转一周,同时射线从开始绕点O以每秒的速度沿顺时针方向旋转,当三角板停止运动时,射线也停止运动.设旋转时间为t秒.
①在运动过程中,当时,求t的值;
②当时,在旋转的过程中与始终满足关系(m,n为常数),求的值.
12.已知,为内部的一条射线,.
(1)如图1,若平分,为内部的一条射线,,求的度数;
(2)如图2,若射线绕着点从开始以每秒的速度顺时针旋转至结束、绕着点从开始以每秒的速度逆时针旋转至结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为秒,当时,求的值;
(3)若射线绕着点从开始以每秒的速度逆时针旋转至结束,在旋转过程中,平分,试问在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及相应所在的时间段.(本题中的角均为大于且小于的角)
13.如图①,已知线段,,线段在线段上运动,、分别是、的中点.
(1)若,则______;
(2)当线段在线段上运动时,试判断的长度是否发生变化?如果不变请求出的长度,如果变化,请说明理由;
(3)我们发现角的很多规律和线段一样,如图②已知在内部转动,、分别平分和,则、和有何数量关系,请直接写出结果不需证明.
14.如图1,O为直线AB上一点,∠AOC=30°,点C在AB的上方.MON为直角三角板,O为直角顶点,,ON在射线OC上.将三角板MON绕点O以每秒6°的速度沿逆时针方向旋转,与此同时,射线OC绕点O以每秒11°的速度沿逆时针方向旋转,当射线OC与射线OA重合时,所有运动都停止.设运动的时间为t秒,
(1)旋转开始前,∠MOC= °,∠BOM= °;
(2)运动t秒时,OM转动了 °,t为 秒时,OC与OM重合;
(3)t为何值时,∠MOC=35°?请说明理由.
15.一个问题解决往往经历发现猜想——探索归纳——问题解决的过程,下面结合一道几何题来体验一下.
【发现猜想】(1)如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;.
【探索归纳】(2)如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线. 猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
【问题解决】(3)如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动. 运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
试卷第1页,共3页
参考答案:
1.(1);
(2)
(3)
2.(1)B
(2)①∠AOC=40°,∠BOC=80°;②40°
3.(1);
(2)①射线是的平分线;②,或,或,或,或,.
4.(1)24
(2)不变化,EF=24cm.
(3)115°
5.(1)和互为垂角(答案不唯一)
(2)
(3)当的值为2或14或时,和互为垂角
6.(1)
(2)的长度不变,EF=6cm
(3)
7.(1)40
(2)①存在,秒或44秒;②,30,,
8.(1)11(2)11cm(3)
9.(1)150°;(2)①秒;②∠BOC的度数为90°-15°t或60°-10°t或25°,对应的t值为或或
10.(1)60
(2)t的值为或
(3)∠ABP=∠CBN或2∠ABP+∠CBN=360゜,
11.(1);
(2)①t的值为10秒或秒或秒;②.
12.(1);(2)t的值为3或7.5;(3)当或时,为定值,
13.(1);(2)的长度不变,;(3).
14.(1),;(2),;(3)秒或秒.
15.(1)85°;(2)∠AOC=;(3)经过,,4秒时,其中一条射线是另外两条射线夹角的平分线.
答案第1页,共2页
动角问题压轴题
1.将一副三角板按图1摆放在直线上,平分,平分.
(1) ; ;
(2)如图2,若将三角板绕点以秒的速度顺时针旋转秒,求的度数;
(3)如图3,三角板绕点以秒的速度顺时针旋转,同时,三角板绕点以秒的速度逆时针旋转,当与边首次重合时两三角板都停止运动,若运行秒时,有成立,试求此时与的关系.
2.直线外有一定点,是直线上的一个动点.
(1)如图1所示,当点从左向右运动时,观察的变化情况,正确的是________
A.逐渐变大 B.逐渐变小 C.大小不变 D.无法确定
(2)当点运动到时,点运动停止,然后将射线绕着点顺时针旋转到如图2位置,且.
①求图2中,的度数;
②在图2的基础上,作射线平分,在内作射线,使得,如图3,求的度数.
3.如图,已知,射线在内部,点B在射线上,在线段的延长线上截取,动点D从点A的位置出发,沿射线的方向运动,与此同时,射线从与射线重合的位置开始绕点A顺时针旋转(点D到达点C时,两者都停止运动).设运动时间为t秒,的角度为,线段的长为l.且,l,t的关系如下:,.(l,m的单位分别为和).
(1)若动点D运动到终点C,求t的值;
(2)当时,
① 若,动点D运动到点B的位置,射线是哪个角的平分线?
②在旋转的同时,射线也绕点A逆时针旋转,旋转速度是每秒,射线旋转后的对应射线记为,若,m,t均为正整数,求m,t的值.
4.
如图1,已知线段AB=44cm,CD=4cm,线段CD在线段AB上运动(点C不与点A重合),点E、F分别是AC、BD的中点.
(1)若AC=10cm,则EF=______cm;
(2)当线段CD在线段AB上运动时,试判断线段EF的长度是否会发生变化,如果不变,请求出线段的长度;如果变化,请说明理由;
(3)我们发现角的很多规律和线段一样,如图2,已知∠COD在∠AOB内部转动,OE,OF分别平分∠AOC和∠BOD.类比以上发现的线段的规律,若∠EOF=75°,∠COD=35°,则∠AOB =______.
5.定义:如果两个角的差的绝对值等于,就称这个两个角互为垂角,例如:,,,则和互为垂角.
(1)如图1,为直线上的一点,,,直接写出图中一对垂角;
(2)如果一个锐角的垂角等于这个角的余角的3倍,求这个角的度数;
(3)如图2,为直线上的一点,若,,且射线绕以每秒的速度顺时针旋转,射线绕点以每秒的速度顺时针旋转,两条射线、同时运动,运动时间为秒,试求当为何值时,和互为垂角?
6.如图①,已知线段在线段上运动,线段,,点、分别是、的中点.解答下列问题:
(1)若,求的长;
(2)当线段在线段上运动时,试判断的长度是否发生变化?如果不变请求出的长度,如果变化,请说明理由;
(3)通过类比,我们发现角的很多规律和线段一样,如图②已知在内部转动,和分别平分和,则与、有何数量关系,请直接写出答案.
7.【阅读理解】射线是内部的一条射线,若,则我们称射线是射线的“友好线”,例如,如图1,,,则,称射线是射线的友好线:同时,由于,称射线是射线的友好线.
(1)如图2,,射线是射线的友好线,则________;
(2)如图3,,射线与射线重合,并绕点以每秒的速度逆时针旋转,射线与射线重合,并绕点以每秒3゜的速度顺时针旋转,当射线与射线重合时,运动停止;
①是否存在某个时刻(秒),使得的度数是,若存在,求出的值,若不存在,请说明理由;
②当为多少秒时,射线、、中恰好有一条射线是另一条射线的友好线.(直接写出答案)
8.如图①,已知线段AB=20cm,CD=2cm,线段CD在线段AB上运动,E、F分别是AC、BD的中点.
(1)若AC=4cm,则EF=_________cm.
(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变请求出EF的长度,如果变化,请说明理由.
(3)我们发现角的很多规律和线段一样,如图②已知在内部转动,OE、OF分别平分在,则、和有何关系,请直接写出_______________________.
9.如图1,已知∠AOB=90°,∠COD=60°,射线OC,OB重合.
(1)∠AOD= ;
(2)如图2,若射线OB以每秒15°的速度绕点O逆时针旋转,同时若射线OC以每秒10°的速度绕点O顺时针旋转,当射线OB与OA重合时,两射线都停止运动,设旋转的时间为t秒,
①当∠BOC=90°时,求t的值;
②如图3,当有一条射线恰好是另外两条射线夹角的角平分线时,直接写出∠BOC的度数 (用t的代数式表示),并求t的值.
10.如图1,正方形和长方形的周长相等,且各有一条边在数轴上,点对应的数分别是.正方形以每秒2个单位长度的速度向右移动,同时长方形以每秒1个单位长度的速度向左移动.设正方形和长方形重叠部分的面积为S,移动时间为t.
(1)长方形的面积是______.
(2)当S是长方形面积的一半时,求t的值.
(3)如图2,当正方形和长方形运动到点B和点F重合时,停止运动,将正方形绕点B顺时针旋转,旋转角度为,点分别在线段、线段的延长线上,平分,判断和之间的数量关系,用等式表示,并说明理由.
11.如图1,点O为直线上一点,过点O作射线,使,将一直角三角板的直角顶点放在点O处(),一边在射线上,另一边在直线的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边在的内部,且恰好平分.求的度数.
(2)将图1中三角板绕点O以每秒的速度沿逆时针方向旋转一周,同时射线从开始绕点O以每秒的速度沿顺时针方向旋转,当三角板停止运动时,射线也停止运动.设旋转时间为t秒.
①在运动过程中,当时,求t的值;
②当时,在旋转的过程中与始终满足关系(m,n为常数),求的值.
12.已知,为内部的一条射线,.
(1)如图1,若平分,为内部的一条射线,,求的度数;
(2)如图2,若射线绕着点从开始以每秒的速度顺时针旋转至结束、绕着点从开始以每秒的速度逆时针旋转至结束,当一条射线到达终点时另一条射线也停止运动.若运动时间为秒,当时,求的值;
(3)若射线绕着点从开始以每秒的速度逆时针旋转至结束,在旋转过程中,平分,试问在某时间段内是否为定值;若不是,请说明理由;若是,请补全图形,并直接写出这个定值以及相应所在的时间段.(本题中的角均为大于且小于的角)
13.如图①,已知线段,,线段在线段上运动,、分别是、的中点.
(1)若,则______;
(2)当线段在线段上运动时,试判断的长度是否发生变化?如果不变请求出的长度,如果变化,请说明理由;
(3)我们发现角的很多规律和线段一样,如图②已知在内部转动,、分别平分和,则、和有何数量关系,请直接写出结果不需证明.
14.如图1,O为直线AB上一点,∠AOC=30°,点C在AB的上方.MON为直角三角板,O为直角顶点,,ON在射线OC上.将三角板MON绕点O以每秒6°的速度沿逆时针方向旋转,与此同时,射线OC绕点O以每秒11°的速度沿逆时针方向旋转,当射线OC与射线OA重合时,所有运动都停止.设运动的时间为t秒,
(1)旋转开始前,∠MOC= °,∠BOM= °;
(2)运动t秒时,OM转动了 °,t为 秒时,OC与OM重合;
(3)t为何值时,∠MOC=35°?请说明理由.
15.一个问题解决往往经历发现猜想——探索归纳——问题解决的过程,下面结合一道几何题来体验一下.
【发现猜想】(1)如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;.
【探索归纳】(2)如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线. 猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
【问题解决】(3)如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动. 运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
试卷第1页,共3页
参考答案:
1.(1);
(2)
(3)
2.(1)B
(2)①∠AOC=40°,∠BOC=80°;②40°
3.(1);
(2)①射线是的平分线;②,或,或,或,或,.
4.(1)24
(2)不变化,EF=24cm.
(3)115°
5.(1)和互为垂角(答案不唯一)
(2)
(3)当的值为2或14或时,和互为垂角
6.(1)
(2)的长度不变,EF=6cm
(3)
7.(1)40
(2)①存在,秒或44秒;②,30,,
8.(1)11(2)11cm(3)
9.(1)150°;(2)①秒;②∠BOC的度数为90°-15°t或60°-10°t或25°,对应的t值为或或
10.(1)60
(2)t的值为或
(3)∠ABP=∠CBN或2∠ABP+∠CBN=360゜,
11.(1);
(2)①t的值为10秒或秒或秒;②.
12.(1);(2)t的值为3或7.5;(3)当或时,为定值,
13.(1);(2)的长度不变,;(3).
14.(1),;(2),;(3)秒或秒.
15.(1)85°;(2)∠AOC=;(3)经过,,4秒时,其中一条射线是另外两条射线夹角的平分线.
答案第1页,共2页
同课章节目录
