2024年中考数学一轮专题复习: 圆与二次函数结合型压轴题
文档属性
| 名称 | 2024年中考数学一轮专题复习: 圆与二次函数结合型压轴题 |

|
|
| 格式 | docx | ||
| 文件大小 | 903.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 00:00:00 | ||
图片预览



文档简介
2024年中考数学一轮专题复习:
圆与二次函数结合型压轴题
1.如图,在Rt△ABC中,∠ACB=90°,BC>AC.以斜边AB所在的直线为x轴,以斜边AB上的高所在直线为y轴建立直角坐标系,若,且线段OA、OB的长度是关于x的一元二次方程-mx+2(m-3)=0的两个根.
(1)求C点的坐标.
(2)以斜边AB为直径作圆,与y轴交于另一点E,求过A、B、E三点的抛物线的解析式.
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点坐标,若不存在,说明理由.
2.我们把方程(x- m)2+(y-n)2=r2称为圆心为(m,n)、半径长为r的圆的标准方程.例如,圆心为(1,-2)、半径长为3的圆的标准方程是(x- 1)2+(y+2)2=9.在平面直角坐标系中,圆C与轴交于点A.B.且点B的坐标为(8.0),与y轴相切于点D(0, 4),过点A,B,D的抛物线的顶点为E.
(1)求圆C的标准方程;
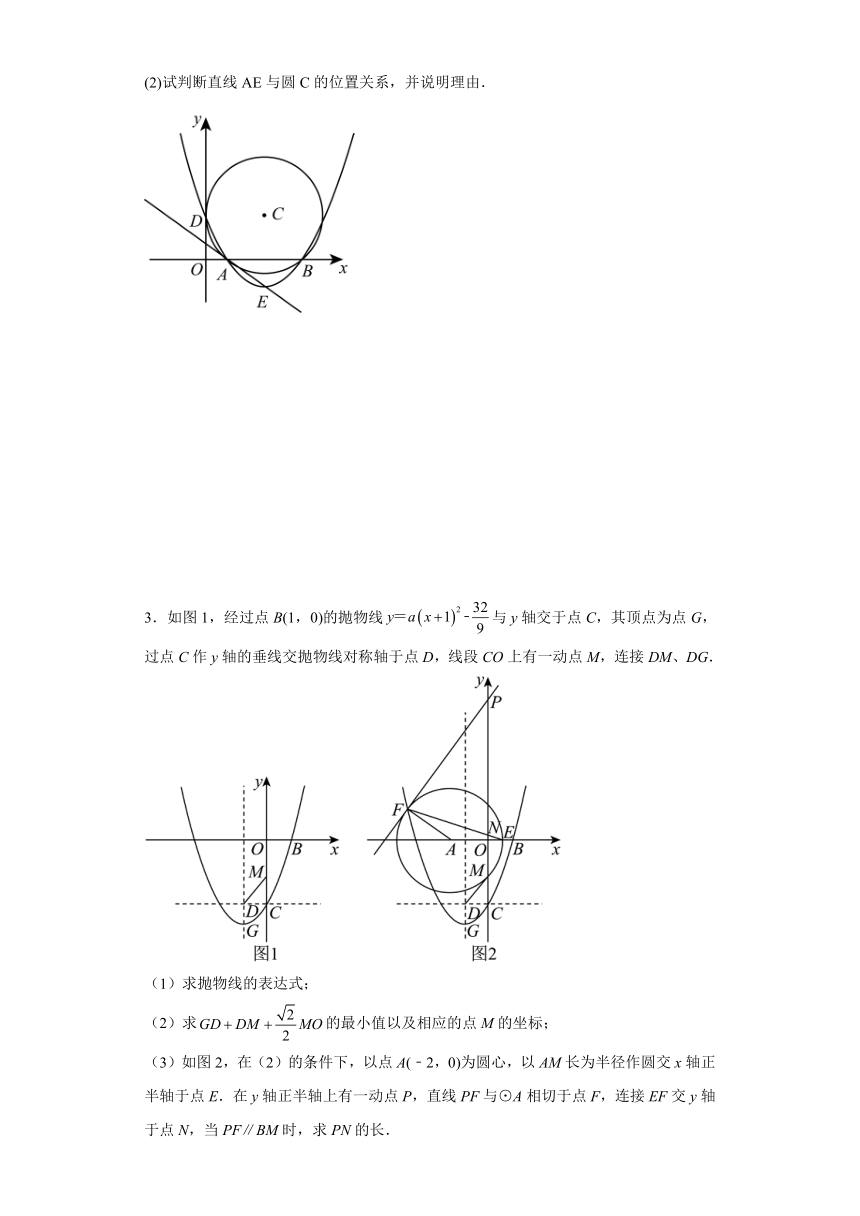
(2)试判断直线AE与圆C的位置关系,并说明理由.
3.如图1,经过点B(1,0)的抛物线与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
(1)求抛物线的表达式;
(2)求的最小值以及相应的点M的坐标;
(3)如图2,在(2)的条件下,以点A(﹣2,0)为圆心,以AM长为半径作圆交x轴正半轴于点E.在y轴正半轴上有一动点P,直线PF与⊙A相切于点F,连接EF交y轴于点N,当PF∥BM时,求PN的长.
4.如图,直线与x轴交于点B,与y轴交于点C,抛物线经过B、C两点,且与x轴交于另一点A.
(1)求抛物线的解析式.
(2)点P是线段BC下方的抛物线上的动点(不与点B、C重合),过P作PD∥y轴交BC于点D,以PD为直径的圆交BC于另一点E,求DE的最大值及此时点P的坐标;
(3)当(2)中的DE取最大值时,将△PDE绕点D旋转,当点P落在坐标轴上时,求点E的坐标.
5.已知:如图,在平面直角坐标系xOy中,点A(0,),点B(1,0),点C(3,0),以点P为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).
(1)求经过A、B、C三点的抛物线的解析式和点P坐标;
(2)求证:四边形ABCP是菱形,并求出菱形ABCP面积;
(3)在(1)中的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的?如果存在,请直接写出所有满足条件的M点的坐标;如果若不存在,请说明理由;
(4)如果点D是抛物线上一动点(不与A,B,C重合),当∠BDC≧30°时,请直接写出所有满足条件的D点的横坐标的范围.
6.直角坐标系xOy中,有反比例函数上的一动点P,以点P为圆心的圆始终与y轴相切,设切点为A
(1)如图1,⊙P运动到与x轴相切时,求OP2的值.
(2)设圆P运动时与x轴相交,交点为B、C,如图2,当四边形ABCP是菱形时,
①求出A、B、C三点的坐标.
②设一抛物线过A、B、C三点,在该抛物线上是否存在点Q,使△QBP的面积是菱形ABCP面积的?若存在,求出所有满足条件的Q点的坐标;若不存在,说明理由.
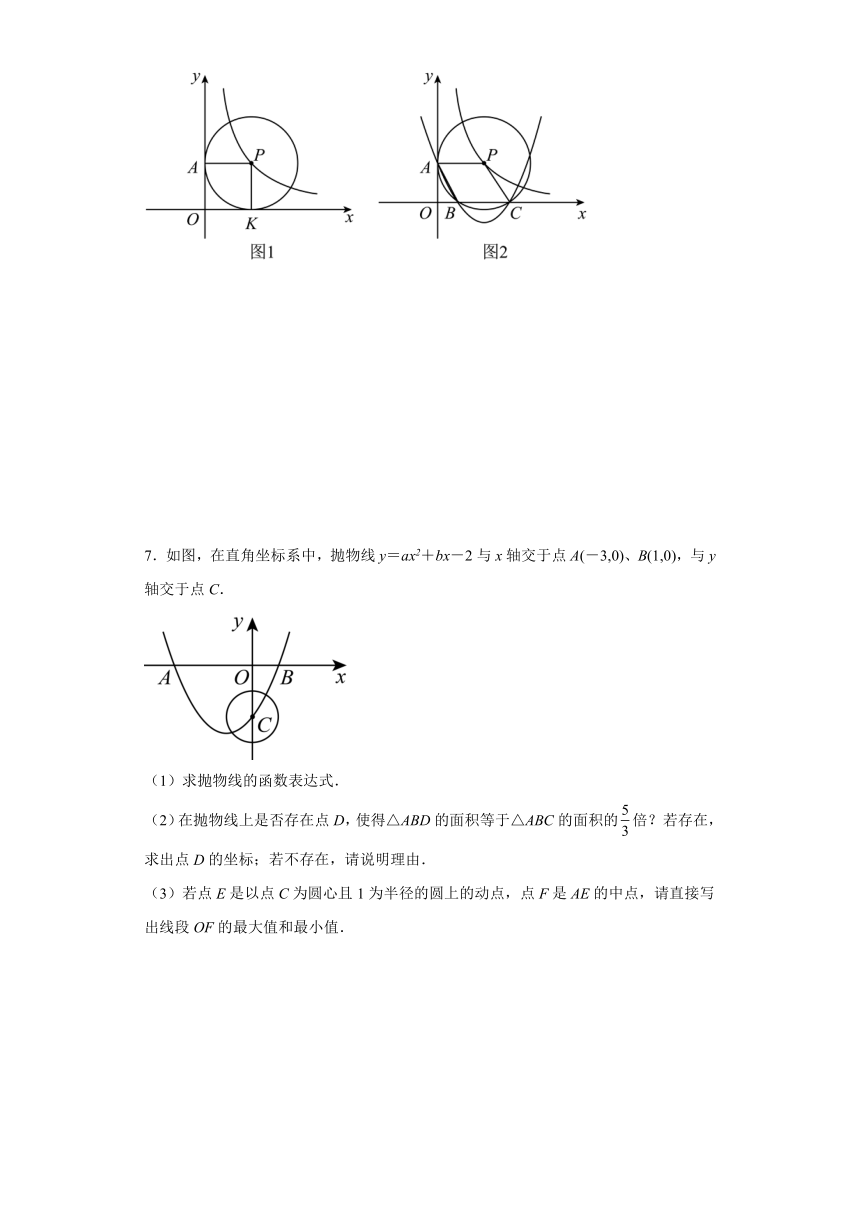
7.如图,在直角坐标系中,抛物线y=ax2+bx-2与x轴交于点A(-3,0)、B(1,0),与y轴交于点C.
(1)求抛物线的函数表达式.
(2)在抛物线上是否存在点D,使得△ABD的面积等于△ABC的面积的倍?若存在,求出点D的坐标;若不存在,请说明理由.
(3)若点E是以点C为圆心且1为半径的圆上的动点,点F是AE的中点,请直接写出线段OF的最大值和最小值.
8.已知,如图,二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),B(3,0),点E为二次函数第一象限内抛物线上一动点,EH⊥x轴于点H,交直线BC于点F,以EF为直径的圆⊙M与BC交于点R.
(1)求这个二次函数关系式.
(2)当△EFR周长最大时.
①求此时点E点坐标及△EFR周长.
②点P为⊙M上一动点,连接BP,点Q为BP的中点,连接HQ,求HQ的最大值.
9.如图,在平面直角坐标系中,顶点为(11,﹣)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,8).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;
(3)连接AC,在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形,若存在,请直接写出点P的坐标,若不存在,请说明理由.
10.如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值并求此时点M的坐标;
(2)如图2,若a=1,,求证:无论b,c取何值,点D均为定点,求出该定点坐标.
11.如图①②,在平面直角坐标系中,边长为2的等边恰好与坐标系中的重合,现将绕边的中点点也是的中点),按顺时针方向旋转到△的位置.
(1)求点的坐标;
(2)求经过三点、、的抛物线的解析式;
(3)如图③,是以为直径的圆,过点作的切线与轴相交于点,求切线的解析式;
(4)抛物线上是否存在一点,使得.若存在,请求出点的坐标;若不存在,请说明理由.
12.如图,已知二次函数(m>0)的图象与x轴交于A、B两点.
(1)写出A、B两点的坐标(坐标用m表示);
(2)若二次函数图象的顶点P在以AB为直径的圆上,求二次函数的解析式;
(3)设以AB为直径的⊙M与y轴交于C、D两点,求CD的长.
13.如图,直线交轴于点,交轴于点,点的坐标为,抛物线经过三点,抛物线的顶点为点,对称轴与轴的交点为点,点关于原点的对称点为,连接,以点为圆心,的长为半径作圆,点为直线上的一个动点.
(1)求抛物线的解析式;
(2)求周长的最小值;
(3)若动点与点不重合,点为⊙上的任意一点,当的最大值等于时,过两点的直线与抛物线交于两点(点在点的左侧),求四边形的面积.
14.如图,直角三角形ABC中,∠ABC=90°,B(2,0),经过A、B、C三点的抛物线y=x2﹣2x+k与y轴交于点A,与x轴的另一个交点为D.
(1)求此抛物线的解析式;
(2)⊙B是以点B为圆心,OB长为半径的圆,以点D为圆心的⊙D与直线BC相切,请你通过计算说明:⊙B与⊙D的位置关系;
(3)在直线AD下方的抛物线上是否存在一点P,使四边形APDC的面积最大?若存在,请你求出点P的坐标和四边形APDC面积的最大值;若不存在,请你说明理由.
15.已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点.
(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
试卷第1页,共3页
参考答案:
1.(1)C(0,2);(2);(3)存在,P(3,-2).
2.(1);(2)相切,
3.(1);(2)最小值,M(0,);(3) .
4.(1)y=x2﹣x﹣2;(2)m=2时,DE有最大值,此时P;(3),或E或
5.(1)yx2x,点P坐标为:P(2,);(2)2;;(3)点M的坐标为(0,),(3,0),(4,),(7,8);(4)0<x<1或1<x<3或3<x≤4.
6.(1)16;(2)①A(0,),B(2,0),C(6,0);②存在,满足条件的Q点有(0,),(14,),(8,)和(6,0).
7.(1);(2)存在,D(-4, )或(2,);(3)最大值; 最小值
8.(1)y=﹣x2+2x+3;(2)①E(,),周长为+;②HQ的最大值大为:+.
9.(1);(2)对称轴l与⊙C相交,(3)P(30,﹣2)或(46,100)
10.(1)①,D(0,4);②M(2-6);(2)(0,1)
11.(1);(2);(3);(4).
12.解:(1)∵,∴当y=0时,.
解得x1=﹣m,x2=3m.
∵m>0,∴A、B两点的坐标分别是(﹣m,0),(3m,0).
(2)∵A(﹣m,0),B(3m,0),m>0,
∴,圆的半径为AB=2m.
∴OM=AM﹣OA=2m﹣m=m.
∴抛物线的顶点P的坐标为:(m,﹣2m).
∵二次函数(m>0)的顶点P的坐标为:(m,﹣4m2),
∴﹣2m=﹣4m2,解得m1=,m2=0(舍去).
∴二次函数的解析式为,即.
(3)如图,连接CM,
在Rt△OCM中,
∵∠COM=90°,CM=2m=2×=1,OM=m=,
∴.
∴CD=2OC=.
13.(1);(2)(3)
14.(1)y=x2﹣2x+3;(2)⊙B与⊙D的位置关系为相交;(3)当x=3,即 P(3,﹣)时,四边形APDC的面积最大,且最大值为.
15.(1)点P的坐标为(,3).
(2)抛物线的解析式为y=﹣x2+6
(3)点A、B、C、D围成的多边形的面积为4+2或6.
答案第1页,共2页
圆与二次函数结合型压轴题
1.如图,在Rt△ABC中,∠ACB=90°,BC>AC.以斜边AB所在的直线为x轴,以斜边AB上的高所在直线为y轴建立直角坐标系,若,且线段OA、OB的长度是关于x的一元二次方程-mx+2(m-3)=0的两个根.
(1)求C点的坐标.
(2)以斜边AB为直径作圆,与y轴交于另一点E,求过A、B、E三点的抛物线的解析式.
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点坐标,若不存在,说明理由.
2.我们把方程(x- m)2+(y-n)2=r2称为圆心为(m,n)、半径长为r的圆的标准方程.例如,圆心为(1,-2)、半径长为3的圆的标准方程是(x- 1)2+(y+2)2=9.在平面直角坐标系中,圆C与轴交于点A.B.且点B的坐标为(8.0),与y轴相切于点D(0, 4),过点A,B,D的抛物线的顶点为E.
(1)求圆C的标准方程;
(2)试判断直线AE与圆C的位置关系,并说明理由.
3.如图1,经过点B(1,0)的抛物线与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
(1)求抛物线的表达式;
(2)求的最小值以及相应的点M的坐标;
(3)如图2,在(2)的条件下,以点A(﹣2,0)为圆心,以AM长为半径作圆交x轴正半轴于点E.在y轴正半轴上有一动点P,直线PF与⊙A相切于点F,连接EF交y轴于点N,当PF∥BM时,求PN的长.
4.如图,直线与x轴交于点B,与y轴交于点C,抛物线经过B、C两点,且与x轴交于另一点A.
(1)求抛物线的解析式.
(2)点P是线段BC下方的抛物线上的动点(不与点B、C重合),过P作PD∥y轴交BC于点D,以PD为直径的圆交BC于另一点E,求DE的最大值及此时点P的坐标;
(3)当(2)中的DE取最大值时,将△PDE绕点D旋转,当点P落在坐标轴上时,求点E的坐标.
5.已知:如图,在平面直角坐标系xOy中,点A(0,),点B(1,0),点C(3,0),以点P为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).
(1)求经过A、B、C三点的抛物线的解析式和点P坐标;
(2)求证:四边形ABCP是菱形,并求出菱形ABCP面积;
(3)在(1)中的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的?如果存在,请直接写出所有满足条件的M点的坐标;如果若不存在,请说明理由;
(4)如果点D是抛物线上一动点(不与A,B,C重合),当∠BDC≧30°时,请直接写出所有满足条件的D点的横坐标的范围.
6.直角坐标系xOy中,有反比例函数上的一动点P,以点P为圆心的圆始终与y轴相切,设切点为A
(1)如图1,⊙P运动到与x轴相切时,求OP2的值.
(2)设圆P运动时与x轴相交,交点为B、C,如图2,当四边形ABCP是菱形时,
①求出A、B、C三点的坐标.
②设一抛物线过A、B、C三点,在该抛物线上是否存在点Q,使△QBP的面积是菱形ABCP面积的?若存在,求出所有满足条件的Q点的坐标;若不存在,说明理由.
7.如图,在直角坐标系中,抛物线y=ax2+bx-2与x轴交于点A(-3,0)、B(1,0),与y轴交于点C.
(1)求抛物线的函数表达式.
(2)在抛物线上是否存在点D,使得△ABD的面积等于△ABC的面积的倍?若存在,求出点D的坐标;若不存在,请说明理由.
(3)若点E是以点C为圆心且1为半径的圆上的动点,点F是AE的中点,请直接写出线段OF的最大值和最小值.
8.已知,如图,二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),B(3,0),点E为二次函数第一象限内抛物线上一动点,EH⊥x轴于点H,交直线BC于点F,以EF为直径的圆⊙M与BC交于点R.
(1)求这个二次函数关系式.
(2)当△EFR周长最大时.
①求此时点E点坐标及△EFR周长.
②点P为⊙M上一动点,连接BP,点Q为BP的中点,连接HQ,求HQ的最大值.
9.如图,在平面直角坐标系中,顶点为(11,﹣)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,8).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;
(3)连接AC,在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形,若存在,请直接写出点P的坐标,若不存在,请说明理由.
10.如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值并求此时点M的坐标;
(2)如图2,若a=1,,求证:无论b,c取何值,点D均为定点,求出该定点坐标.
11.如图①②,在平面直角坐标系中,边长为2的等边恰好与坐标系中的重合,现将绕边的中点点也是的中点),按顺时针方向旋转到△的位置.
(1)求点的坐标;
(2)求经过三点、、的抛物线的解析式;
(3)如图③,是以为直径的圆,过点作的切线与轴相交于点,求切线的解析式;
(4)抛物线上是否存在一点,使得.若存在,请求出点的坐标;若不存在,请说明理由.
12.如图,已知二次函数(m>0)的图象与x轴交于A、B两点.
(1)写出A、B两点的坐标(坐标用m表示);
(2)若二次函数图象的顶点P在以AB为直径的圆上,求二次函数的解析式;
(3)设以AB为直径的⊙M与y轴交于C、D两点,求CD的长.
13.如图,直线交轴于点,交轴于点,点的坐标为,抛物线经过三点,抛物线的顶点为点,对称轴与轴的交点为点,点关于原点的对称点为,连接,以点为圆心,的长为半径作圆,点为直线上的一个动点.
(1)求抛物线的解析式;
(2)求周长的最小值;
(3)若动点与点不重合,点为⊙上的任意一点,当的最大值等于时,过两点的直线与抛物线交于两点(点在点的左侧),求四边形的面积.
14.如图,直角三角形ABC中,∠ABC=90°,B(2,0),经过A、B、C三点的抛物线y=x2﹣2x+k与y轴交于点A,与x轴的另一个交点为D.
(1)求此抛物线的解析式;
(2)⊙B是以点B为圆心,OB长为半径的圆,以点D为圆心的⊙D与直线BC相切,请你通过计算说明:⊙B与⊙D的位置关系;
(3)在直线AD下方的抛物线上是否存在一点P,使四边形APDC的面积最大?若存在,请你求出点P的坐标和四边形APDC面积的最大值;若不存在,请你说明理由.
15.已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点.
(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
试卷第1页,共3页
参考答案:
1.(1)C(0,2);(2);(3)存在,P(3,-2).
2.(1);(2)相切,
3.(1);(2)最小值,M(0,);(3) .
4.(1)y=x2﹣x﹣2;(2)m=2时,DE有最大值,此时P;(3),或E或
5.(1)yx2x,点P坐标为:P(2,);(2)2;;(3)点M的坐标为(0,),(3,0),(4,),(7,8);(4)0<x<1或1<x<3或3<x≤4.
6.(1)16;(2)①A(0,),B(2,0),C(6,0);②存在,满足条件的Q点有(0,),(14,),(8,)和(6,0).
7.(1);(2)存在,D(-4, )或(2,);(3)最大值; 最小值
8.(1)y=﹣x2+2x+3;(2)①E(,),周长为+;②HQ的最大值大为:+.
9.(1);(2)对称轴l与⊙C相交,(3)P(30,﹣2)或(46,100)
10.(1)①,D(0,4);②M(2-6);(2)(0,1)
11.(1);(2);(3);(4).
12.解:(1)∵,∴当y=0时,.
解得x1=﹣m,x2=3m.
∵m>0,∴A、B两点的坐标分别是(﹣m,0),(3m,0).
(2)∵A(﹣m,0),B(3m,0),m>0,
∴,圆的半径为AB=2m.
∴OM=AM﹣OA=2m﹣m=m.
∴抛物线的顶点P的坐标为:(m,﹣2m).
∵二次函数(m>0)的顶点P的坐标为:(m,﹣4m2),
∴﹣2m=﹣4m2,解得m1=,m2=0(舍去).
∴二次函数的解析式为,即.
(3)如图,连接CM,
在Rt△OCM中,
∵∠COM=90°,CM=2m=2×=1,OM=m=,
∴.
∴CD=2OC=.
13.(1);(2)(3)
14.(1)y=x2﹣2x+3;(2)⊙B与⊙D的位置关系为相交;(3)当x=3,即 P(3,﹣)时,四边形APDC的面积最大,且最大值为.
15.(1)点P的坐标为(,3).
(2)抛物线的解析式为y=﹣x2+6
(3)点A、B、C、D围成的多边形的面积为4+2或6.
答案第1页,共2页
同课章节目录
