第三章 一元一次方程——应用题常见题型集中训练 人教版数学七年级上册(含答案)
文档属性
| 名称 | 第三章 一元一次方程——应用题常见题型集中训练 人教版数学七年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 213.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 00:00:00 | ||
图片预览




文档简介
第三章 一元一次方程——应用题常见题型集中训练
某药店有两种口罩,甲种口罩每包比乙种口罩每包进价少10元,而它们的售后的利润相同.其中甲种口罩每包的盈利率为,乙种口罩每包的盈利率为,如果该药店某月出售甲种口罩150包,乙种口罩100包,求这个月该药店出售口罩的利润额.
2.为提高学生的运算能力,我县某学校七年级在元旦之前组织了一次数学速算比赛.速算规则如下:速算试题形式为计算题,共20道题,答对一题得5分,不答或错一题倒扣1分.梓萌同学代表班级参加了这次比赛,请解决下列问题:
(1)如果梓萌同学最后得分为76分,那么她计算对了多少道题?
(2)梓萌同学的最后得分可能为85分吗?请说明理由.
3.数轴上的点对应的数是,一只蚂蚁从点出发沿着数轴以每秒个单位长度的速度爬行,当它到达数轴上的点后,立即沿原路原速返回点,共用去秒.
(1)蚂蚁爬行的路程是多少?
(2)点对应的数是多少?
4.10名老师带领若干名学生研学(研学费统一支付),他们联系了标价相同的两家旅行社,经洽谈,A旅行社给的优惠条件是教师全额付费,学生按六折付费;B旅行社给的优惠条件是全体师生按七折付费.
(1)学生有多少人时,两家旅行社收费相等?
(2)现有学生 40人,那么他们选哪一家旅行社研学费用少些呢?
5.某开发公司生产出若干件新产品,需要精加工后才能投放市场,现有甲、乙两个工厂每天分别能加工这种产品16件和24件,已知甲单独加工这批产品比乙单独加工这批产品要多用20天,又知若由甲厂单独做,公司需付甲厂每天加工费用80元;若由乙厂单独做,公司需付乙厂每天加工费用120元。
(1)求这批新产品共有多少件?
(2)若公司董事会制定了如下方案:可以由每个工厂单独完成,也可以由两个工厂合作完成,但在加工过程中,公司需派一名工程师到工厂进行技术指导,并由公司为其提供每天10元的午餐补助,请你帮助公司选择一种既省时又省钱的加工方案,并通过计算说明理由.
6.永兴冰糖橙是“中国十大名橙”,获得过“国家地理标志保护产品”“中国中部(湖南)农业博览会产品金奖”等荣誉.某市场销售大、小两种冰糖橙,价格如下表:
类别 大冰糖橙 小冰糖橙
每千克的价格 10元 6元
李明计划购买大、小冰糖橙共40千克,按此表价格需付款360元.
(1)李明计划购买大、小冰糖橙各多少千克?
(2)该市场甲、乙两店为了扩大销售,采用了不同的优惠方案:在甲店每购买10千克大冰糖橙送1千克小冰糖橙;乙店按价格表的九折销售.问李明选择哪家店购买更省钱.
7.定义:点M、N是数轴上不重合的两点,当数轴上的点P满足,则称点P是点M和点N的“双倍点”.
已知:点O、A、B在数轴上表示的数分别为0、a、b,回答下面的问题:
(1)当,时,点A和点B的“双倍点”所表示的数为:______;
(2)当且时,如果O、A、B中恰有一点是另外两个点的“双倍点”,则______;
(3)若,,点C、D在数轴上表示的数分别为、,线段和点B同时沿数轴正方向移动,点B的速度是每秒3个单位长度,线段的速度是每秒8个单位长度,设运动的时间为t秒,当线段上存在点A和点B的“双倍点”时,求t的取值范围.
8.某商场用1170元购进A、B两种新型节能台灯共30盏,这两种台灯的进价、标价如下表所示.
类型 价格 A型 B型
进价(元/盏) 30 45
标价(元/盏) 50 70
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?
9.为鼓励居民节约用电,某地对居民用户用电收费标准作如下规定:每户每月用电如果不超过度,那么每度按元收费;如果超过度不超过度,那么超过的部分每度按元收费;如果超过度,那么超过的部分每度按元收费.
(1)若居民甲在月份用电度,则他这个月应缴纳电费___________元;
若居民乙在月份用电度,则他这个月应缴纳电费__________元;
若居民丙在月份用电度,则他这个月应缴纳电费_____________元;
若某户居民在月份缴纳电费元,那么他这个月用电多少度?
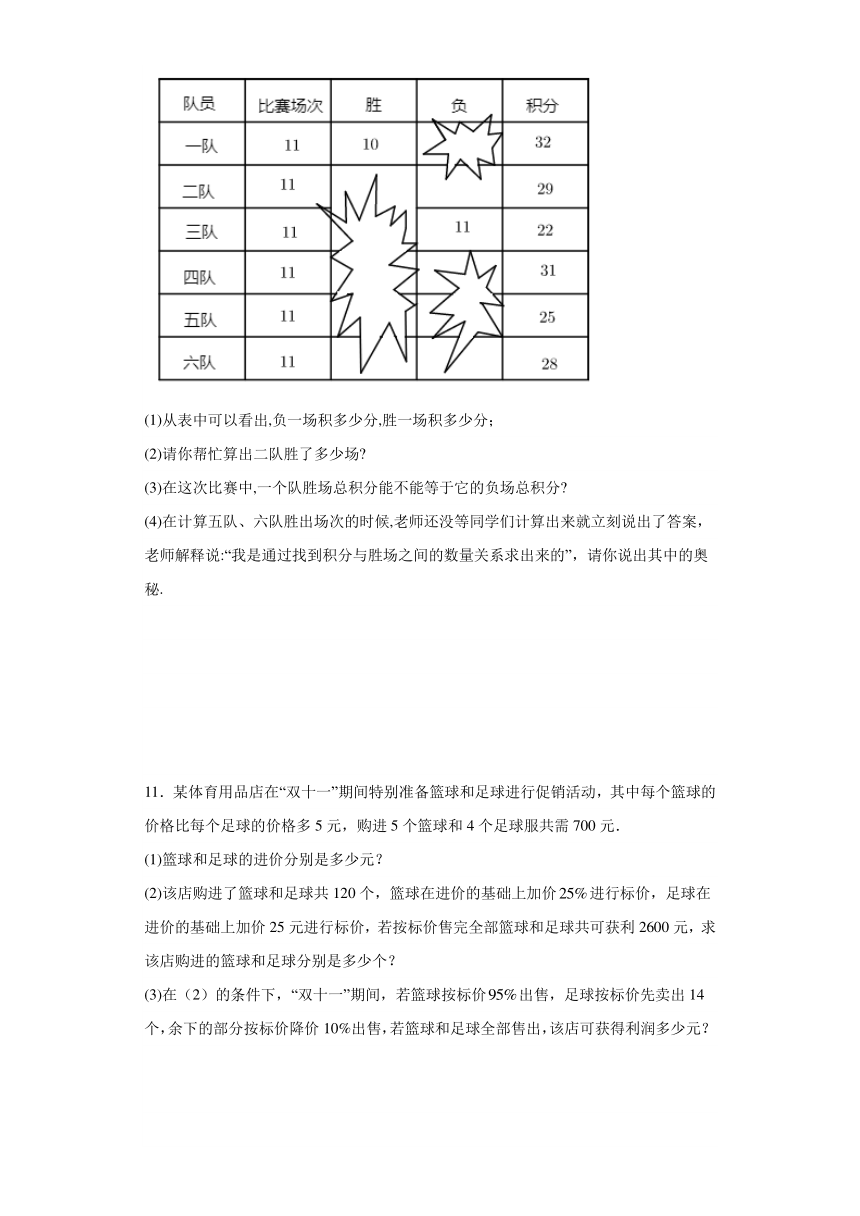
10.数学课上,教师出示某区篮球赛积分表如下:
(1)从表中可以看出,负一场积多少分,胜一场积多少分;
(2)请你帮忙算出二队胜了多少场
(3)在这次比赛中,一个队胜场总积分能不能等于它的负场总积分
(4)在计算五队、六队胜出场次的时候,老师还没等同学们计算出来就立刻说出了答案,老师解释说:“我是通过找到积分与胜场之间的数量关系求出来的”,请你说出其中的奥秘.
11.某体育用品店在“双十一”期间特别准备篮球和足球进行促销活动,其中每个篮球的价格比每个足球的价格多5元,购进5个篮球和4个足球服共需700元.
(1)篮球和足球的进价分别是多少元?
(2)该店购进了篮球和足球共120个,篮球在进价的基础上加价进行标价,足球在进价的基础上加价25元进行标价,若按标价售完全部篮球和足球共可获利2600元,求该店购进的篮球和足球分别是多少个?
(3)在(2)的条件下,“双十一”期间,若篮球按标价出售,足球按标价先卖出14个,余下的部分按标价降价10%出售,若篮球和足球全部售出,该店可获得利润多少元?
12.某市城市居民用电收费方式有以下两种:
普通电价:全天0.52元/千瓦时;
峰谷电价:峰时0.55元/千瓦时(8:00~21:00);谷时0.35元/千瓦时(21:00~次日8:00).
小明家所在小区经过电表升级改造之后下月起实施峰谷电价,已知小明家下月计划总用电量为400千瓦时.
(1)若其中峰时用电量控制为100千瓦时,则小明家下月所付电费比按普通电价收费时省多少元?
(2)当峰时用电量为多少时,小明家下月所付电费跟以往普通电价收费相同?
13.第届亚洲夏季运动会于年月日在杭州举行,象征杭州三大世界文化遗产的吉祥物“宸宸”“琮琮”“莲莲”通过不同色彩、不同纹饰向世界讲述“江南忆”的美丽故事,现有工厂生产吉祥物的盲盒,分为、两种包装,该工厂共有名工人.
(1)若该工厂生产盲盒的人数比生产盲盒的人数的倍少人,请求出生产盲盒的工人人数;
(2)为了促销,工厂按商家要求生产盲盒大礼包,该大礼包由个盲盒和个盲盒组成,已知每个工人平均每天可以生产个盲盒或个盲盒,且每天只能生产一种包装的盲盒.该工厂应该安排多少名工人生产盲盒,多少名工人生产盲盒才能使每天生产的盲盒正好配套?
14.注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,完成填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.
《孙子算经》中有这样一个问题:“今有三人共车,二车空;二人共车,九人步,问人和车各几何?”这个题的意思是:今有若干人乘车,若每3人乘一辆车,则余2辆空车;若每2人乘一辆车,则余9人需步行,问共有多少辆车,多少人?
(1)设有x辆车,根据题意,用含有x的式子填空:
“若每3人乘一辆车,则余2辆空车”即共有________辆车坐满3人,则乘车人数可表示为________;“若每2人乘一辆车,则余9人需步行”即共有________辆车坐满2人,则乘车人数可表示为________.
列出方程,求出问题的答案并写出答话.
15.数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现了许多重要的规律;若数轴上点A、点B表示的数分别为a,b,则A,B两点之间的距离,线段AB的中点表示的数为.
(1)已知数轴上A点对应的数是40,点B对应的数是,则A、B两点之间的距离为_____,线段AB的中点表示的数是_____.
(2)在(1)条件下,如图1,O表示原点,动点P、T分别从B、O两点同时出发向左运动,同时动点Q从点A出发向右运动,点P、T、Q的速度分别为5个单位长度/秒、1个单位长度/秒,2个单位长度/秒,设运动时间为t秒.在运动过程中,如果点M为线段的中点,点N为线段的中点,线段与有何关系?并说明理由.
(3)如图2,若A、B、C三点对应的数分别为,0,30.当A、C两点同时向左运动,同时B点向右运动,已知点A、B、C的速度分别为5个单位长度/秒、3个单位长度/秒、1个单位长度/秒,点M为线段的中点,点N为线段的中点,当运动时间为多少秒时恰好满足:.
试卷第1页,共3页
参考答案:
1.这个月该店出售口罩的利润额是元
2.(1)16道;(2)不能,
3.(1)个单位长度
(2)或
4.(1)个学生
(2)选A旅行社研学费用少些,
5.(1)这批新产品共有960件.
(2)甲、乙合作同时完成时,既省钱又省时间,
6.(1)李明计划购买大冰糖橙30千克,购买小冰糖橙10千克
(2)李明选择乙店购买更省钱
7.(1)3或11
(2)或或或
(3)或
8.(1)A型台灯购进12台,B型台灯购进18台
(2)这批台灯全部售出后,商场共获利378元
9.(1),,
(2)度.
10.(1)负1场积分2分;胜1场积3分;(2)二队胜了7场;(3)不能;(4)积分与获胜的场数之差=22.
11.(1)篮球的进价为80元,足球的进价为75元;
(2)购进的篮球80个,足球40个
(3)该店可获得利润1940元
12.(1)省48元.
(2)340千瓦时
13.(1)生产盲盒的工人人数为人
(2)该工厂应该安排名工人生产,名工人生产才能使每天生产的盲盒正好配套
14.(1),,,
15.(1)120,
(2),
(3)2秒或35秒
答案第1页,共2页
某药店有两种口罩,甲种口罩每包比乙种口罩每包进价少10元,而它们的售后的利润相同.其中甲种口罩每包的盈利率为,乙种口罩每包的盈利率为,如果该药店某月出售甲种口罩150包,乙种口罩100包,求这个月该药店出售口罩的利润额.
2.为提高学生的运算能力,我县某学校七年级在元旦之前组织了一次数学速算比赛.速算规则如下:速算试题形式为计算题,共20道题,答对一题得5分,不答或错一题倒扣1分.梓萌同学代表班级参加了这次比赛,请解决下列问题:
(1)如果梓萌同学最后得分为76分,那么她计算对了多少道题?
(2)梓萌同学的最后得分可能为85分吗?请说明理由.
3.数轴上的点对应的数是,一只蚂蚁从点出发沿着数轴以每秒个单位长度的速度爬行,当它到达数轴上的点后,立即沿原路原速返回点,共用去秒.
(1)蚂蚁爬行的路程是多少?
(2)点对应的数是多少?
4.10名老师带领若干名学生研学(研学费统一支付),他们联系了标价相同的两家旅行社,经洽谈,A旅行社给的优惠条件是教师全额付费,学生按六折付费;B旅行社给的优惠条件是全体师生按七折付费.
(1)学生有多少人时,两家旅行社收费相等?
(2)现有学生 40人,那么他们选哪一家旅行社研学费用少些呢?
5.某开发公司生产出若干件新产品,需要精加工后才能投放市场,现有甲、乙两个工厂每天分别能加工这种产品16件和24件,已知甲单独加工这批产品比乙单独加工这批产品要多用20天,又知若由甲厂单独做,公司需付甲厂每天加工费用80元;若由乙厂单独做,公司需付乙厂每天加工费用120元。
(1)求这批新产品共有多少件?
(2)若公司董事会制定了如下方案:可以由每个工厂单独完成,也可以由两个工厂合作完成,但在加工过程中,公司需派一名工程师到工厂进行技术指导,并由公司为其提供每天10元的午餐补助,请你帮助公司选择一种既省时又省钱的加工方案,并通过计算说明理由.
6.永兴冰糖橙是“中国十大名橙”,获得过“国家地理标志保护产品”“中国中部(湖南)农业博览会产品金奖”等荣誉.某市场销售大、小两种冰糖橙,价格如下表:
类别 大冰糖橙 小冰糖橙
每千克的价格 10元 6元
李明计划购买大、小冰糖橙共40千克,按此表价格需付款360元.
(1)李明计划购买大、小冰糖橙各多少千克?
(2)该市场甲、乙两店为了扩大销售,采用了不同的优惠方案:在甲店每购买10千克大冰糖橙送1千克小冰糖橙;乙店按价格表的九折销售.问李明选择哪家店购买更省钱.
7.定义:点M、N是数轴上不重合的两点,当数轴上的点P满足,则称点P是点M和点N的“双倍点”.
已知:点O、A、B在数轴上表示的数分别为0、a、b,回答下面的问题:
(1)当,时,点A和点B的“双倍点”所表示的数为:______;
(2)当且时,如果O、A、B中恰有一点是另外两个点的“双倍点”,则______;
(3)若,,点C、D在数轴上表示的数分别为、,线段和点B同时沿数轴正方向移动,点B的速度是每秒3个单位长度,线段的速度是每秒8个单位长度,设运动的时间为t秒,当线段上存在点A和点B的“双倍点”时,求t的取值范围.
8.某商场用1170元购进A、B两种新型节能台灯共30盏,这两种台灯的进价、标价如下表所示.
类型 价格 A型 B型
进价(元/盏) 30 45
标价(元/盏) 50 70
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?
9.为鼓励居民节约用电,某地对居民用户用电收费标准作如下规定:每户每月用电如果不超过度,那么每度按元收费;如果超过度不超过度,那么超过的部分每度按元收费;如果超过度,那么超过的部分每度按元收费.
(1)若居民甲在月份用电度,则他这个月应缴纳电费___________元;
若居民乙在月份用电度,则他这个月应缴纳电费__________元;
若居民丙在月份用电度,则他这个月应缴纳电费_____________元;
若某户居民在月份缴纳电费元,那么他这个月用电多少度?
10.数学课上,教师出示某区篮球赛积分表如下:
(1)从表中可以看出,负一场积多少分,胜一场积多少分;
(2)请你帮忙算出二队胜了多少场
(3)在这次比赛中,一个队胜场总积分能不能等于它的负场总积分
(4)在计算五队、六队胜出场次的时候,老师还没等同学们计算出来就立刻说出了答案,老师解释说:“我是通过找到积分与胜场之间的数量关系求出来的”,请你说出其中的奥秘.
11.某体育用品店在“双十一”期间特别准备篮球和足球进行促销活动,其中每个篮球的价格比每个足球的价格多5元,购进5个篮球和4个足球服共需700元.
(1)篮球和足球的进价分别是多少元?
(2)该店购进了篮球和足球共120个,篮球在进价的基础上加价进行标价,足球在进价的基础上加价25元进行标价,若按标价售完全部篮球和足球共可获利2600元,求该店购进的篮球和足球分别是多少个?
(3)在(2)的条件下,“双十一”期间,若篮球按标价出售,足球按标价先卖出14个,余下的部分按标价降价10%出售,若篮球和足球全部售出,该店可获得利润多少元?
12.某市城市居民用电收费方式有以下两种:
普通电价:全天0.52元/千瓦时;
峰谷电价:峰时0.55元/千瓦时(8:00~21:00);谷时0.35元/千瓦时(21:00~次日8:00).
小明家所在小区经过电表升级改造之后下月起实施峰谷电价,已知小明家下月计划总用电量为400千瓦时.
(1)若其中峰时用电量控制为100千瓦时,则小明家下月所付电费比按普通电价收费时省多少元?
(2)当峰时用电量为多少时,小明家下月所付电费跟以往普通电价收费相同?
13.第届亚洲夏季运动会于年月日在杭州举行,象征杭州三大世界文化遗产的吉祥物“宸宸”“琮琮”“莲莲”通过不同色彩、不同纹饰向世界讲述“江南忆”的美丽故事,现有工厂生产吉祥物的盲盒,分为、两种包装,该工厂共有名工人.
(1)若该工厂生产盲盒的人数比生产盲盒的人数的倍少人,请求出生产盲盒的工人人数;
(2)为了促销,工厂按商家要求生产盲盒大礼包,该大礼包由个盲盒和个盲盒组成,已知每个工人平均每天可以生产个盲盒或个盲盒,且每天只能生产一种包装的盲盒.该工厂应该安排多少名工人生产盲盒,多少名工人生产盲盒才能使每天生产的盲盒正好配套?
14.注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,完成填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.
《孙子算经》中有这样一个问题:“今有三人共车,二车空;二人共车,九人步,问人和车各几何?”这个题的意思是:今有若干人乘车,若每3人乘一辆车,则余2辆空车;若每2人乘一辆车,则余9人需步行,问共有多少辆车,多少人?
(1)设有x辆车,根据题意,用含有x的式子填空:
“若每3人乘一辆车,则余2辆空车”即共有________辆车坐满3人,则乘车人数可表示为________;“若每2人乘一辆车,则余9人需步行”即共有________辆车坐满2人,则乘车人数可表示为________.
列出方程,求出问题的答案并写出答话.
15.数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现了许多重要的规律;若数轴上点A、点B表示的数分别为a,b,则A,B两点之间的距离,线段AB的中点表示的数为.
(1)已知数轴上A点对应的数是40,点B对应的数是,则A、B两点之间的距离为_____,线段AB的中点表示的数是_____.
(2)在(1)条件下,如图1,O表示原点,动点P、T分别从B、O两点同时出发向左运动,同时动点Q从点A出发向右运动,点P、T、Q的速度分别为5个单位长度/秒、1个单位长度/秒,2个单位长度/秒,设运动时间为t秒.在运动过程中,如果点M为线段的中点,点N为线段的中点,线段与有何关系?并说明理由.
(3)如图2,若A、B、C三点对应的数分别为,0,30.当A、C两点同时向左运动,同时B点向右运动,已知点A、B、C的速度分别为5个单位长度/秒、3个单位长度/秒、1个单位长度/秒,点M为线段的中点,点N为线段的中点,当运动时间为多少秒时恰好满足:.
试卷第1页,共3页
参考答案:
1.这个月该店出售口罩的利润额是元
2.(1)16道;(2)不能,
3.(1)个单位长度
(2)或
4.(1)个学生
(2)选A旅行社研学费用少些,
5.(1)这批新产品共有960件.
(2)甲、乙合作同时完成时,既省钱又省时间,
6.(1)李明计划购买大冰糖橙30千克,购买小冰糖橙10千克
(2)李明选择乙店购买更省钱
7.(1)3或11
(2)或或或
(3)或
8.(1)A型台灯购进12台,B型台灯购进18台
(2)这批台灯全部售出后,商场共获利378元
9.(1),,
(2)度.
10.(1)负1场积分2分;胜1场积3分;(2)二队胜了7场;(3)不能;(4)积分与获胜的场数之差=22.
11.(1)篮球的进价为80元,足球的进价为75元;
(2)购进的篮球80个,足球40个
(3)该店可获得利润1940元
12.(1)省48元.
(2)340千瓦时
13.(1)生产盲盒的工人人数为人
(2)该工厂应该安排名工人生产,名工人生产才能使每天生产的盲盒正好配套
14.(1),,,
15.(1)120,
(2),
(3)2秒或35秒
答案第1页,共2页
