一元二次方程复习(云南省昆明市五华区)
文档属性
| 名称 | 一元二次方程复习(云南省昆明市五华区) |  | |
| 格式 | rar | ||
| 文件大小 | 19.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-06 12:43:00 | ||
图片预览

文档简介
《一元二次方程》复习
云师大五华实验中学 杨春
一、教学目标
1、复习一元二次方程的概念,明确二次项系数不为零的重要性。
2、一元二次方程根的判别式正反逆用。
3、复习一元二次方程解决一类重要题型——“面积类”问题。
二、教学重难点:
重点:构建一元二次方程的知识体系,能用应用一元二次方程的知识解决问题。
难点:寻求题目中的等量关系,并正确列出方程。
三、教学过程
教学内容 师生活动 设计意图
一、复习一元二次方程的知识体系 一元二次方程的概念一元二 解一元二次方程的方法次方程 一元二次方程的应用 教师引导,学生回顾 引导、帮助学生从宏观上把握本章知识。
二、练一练11、若方程是关于x的一元二次方程,则m= .2、若方程是关于x的一元二次方程,则m= .3、若方程是关于x的一元二次方程,则m= .练一练24、(2007年 巴中)一元二次方程的根的情况为( )A、有两个不相等的实数根 B、有两个相等实数根C、只有一个实数根 D、 没有实数根5、(2008年 威海市) 关于x的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等实数根C、没有实数根 D、无法确定6、(2008年 长沙市)当m 时,关于x的一元二次方程有两个相等的实数根,此时方程的解为 。7、(2007年 攀枝花)已知关于x的一元二次方程有两个不相等的实数根,则的取值范围是 学生自主解答,教师就学生的解答进行点评。学生动手解答问题学生独立完成,教师点评。 通过“练一练1”,重点强调一元二次方程关键是未知数的次数为2次且二次项系数不能为零。让学生熟练运用一元二次方程根的判别式解题,关注中考热点。
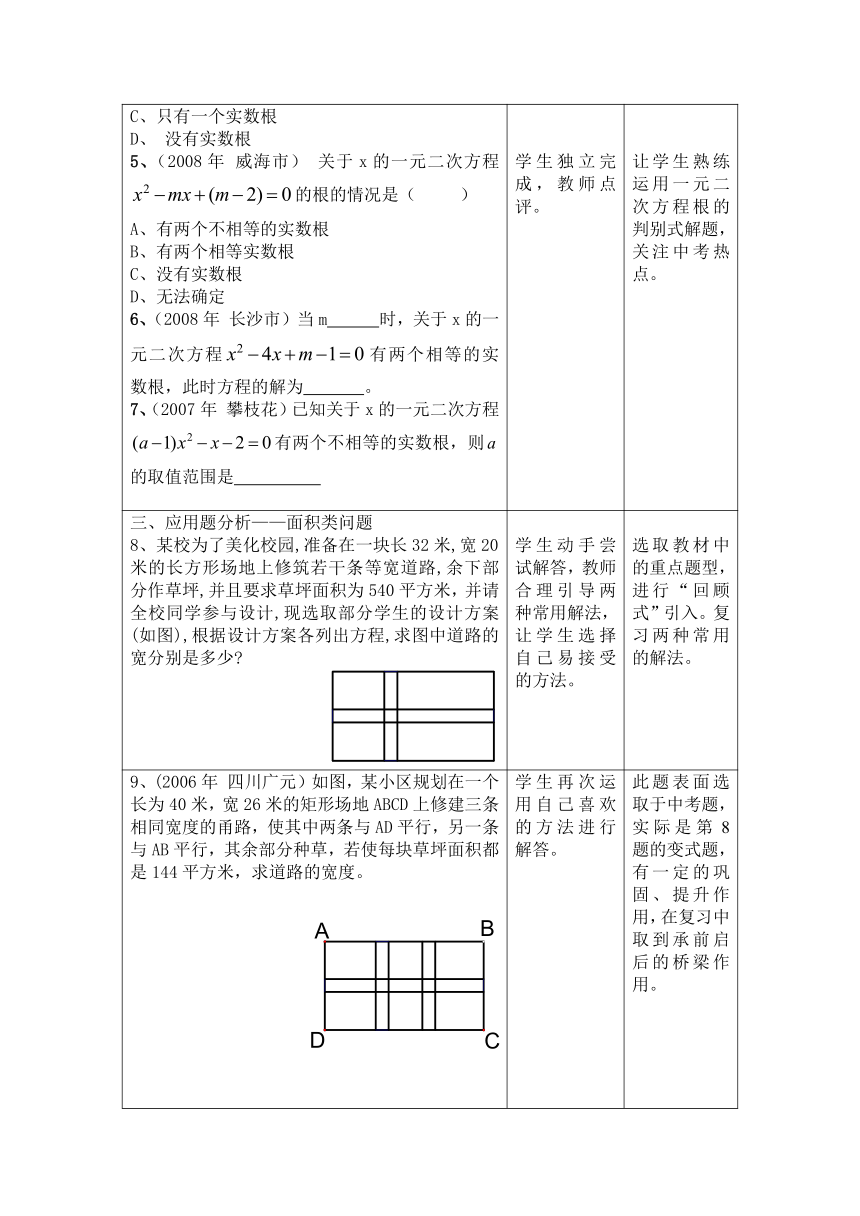
三、应用题分析——面积类问题8、某校为了美化校园,准备在一块长32米,宽20米的长方形场地上修筑若干条等宽道路,余下部分作草坪,并且要求草坪面积为540平方米,并请全校同学参与设计,现选取部分学生的设计方案(如图),根据设计方案各列出方程,求图中道路的宽分别是多少 学生动手尝试解答,教师合理引导两种常用解法,让学生选择自己易接受的方法。 选取教材中的重点题型,进行“回顾式”引入。复习两种常用的解法。
9、(2006年 四川广元)如图,某小区规划在一个长为40米,宽26米的矩形场地ABCD上修建三条相同宽度的甬路,使其中两条与AD平行,另一条与AB平行,其余部分种草,若使每块草坪面积都是144平方米,求道路的宽度。 10、如下图设计方案,长32米,宽20米,各道路的宽度相等,草坪的总面积为540平方米,求道路的宽?11、要设计一幅长为20cm,宽为10cm的图案,其中有两横两竖的彩条,横竖彩条的宽度比为2:1,如果要使剩下面积为152cm2, 应如何设计彩条的宽度?12、提出思考问题。“在矩形中,修多条路时,如何求求路宽的方法?”(备用思考题)如图,某小区计划在一块梯形草地上修建三条宽度相同的小路,该梯形上底16米,下底40米,高26米,在两腰中点连线处有一条横向小路,上下两底之间有两条纵向小路,各小路宽度相等,剩余草地面积为576平方米,小路的宽是多少? 学生再次运用自己喜欢的方法进行解答。学生自主思考,探讨解决问题的方法学生积极尝试,教师引导讲评。学生归纳总结此类题的方法。学生尝试解决,教师启发思路。 此题表面选取于中考题,实际是第8题的变式题,有一定的巩固、提升作用,在复习中取到承前启后的桥梁作用。将方法应用到题中,感受“平移法中的有效性和必要性”,对学生的思维层次进行了必要的提升,感受“平移法”重要作用。此题是上面题的变式题,从“等宽”变形到“不等宽”,可以真正理解平移法的精髓。归纳方法,将解题方法一般化,使学生能够触类旁通,解决此类问题。将矩形问题扩展到等腰梯形。
三、课堂小结
云师大五华实验中学 杨春
一、教学目标
1、复习一元二次方程的概念,明确二次项系数不为零的重要性。
2、一元二次方程根的判别式正反逆用。
3、复习一元二次方程解决一类重要题型——“面积类”问题。
二、教学重难点:
重点:构建一元二次方程的知识体系,能用应用一元二次方程的知识解决问题。
难点:寻求题目中的等量关系,并正确列出方程。
三、教学过程
教学内容 师生活动 设计意图
一、复习一元二次方程的知识体系 一元二次方程的概念一元二 解一元二次方程的方法次方程 一元二次方程的应用 教师引导,学生回顾 引导、帮助学生从宏观上把握本章知识。
二、练一练11、若方程是关于x的一元二次方程,则m= .2、若方程是关于x的一元二次方程,则m= .3、若方程是关于x的一元二次方程,则m= .练一练24、(2007年 巴中)一元二次方程的根的情况为( )A、有两个不相等的实数根 B、有两个相等实数根C、只有一个实数根 D、 没有实数根5、(2008年 威海市) 关于x的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等实数根C、没有实数根 D、无法确定6、(2008年 长沙市)当m 时,关于x的一元二次方程有两个相等的实数根,此时方程的解为 。7、(2007年 攀枝花)已知关于x的一元二次方程有两个不相等的实数根,则的取值范围是 学生自主解答,教师就学生的解答进行点评。学生动手解答问题学生独立完成,教师点评。 通过“练一练1”,重点强调一元二次方程关键是未知数的次数为2次且二次项系数不能为零。让学生熟练运用一元二次方程根的判别式解题,关注中考热点。
三、应用题分析——面积类问题8、某校为了美化校园,准备在一块长32米,宽20米的长方形场地上修筑若干条等宽道路,余下部分作草坪,并且要求草坪面积为540平方米,并请全校同学参与设计,现选取部分学生的设计方案(如图),根据设计方案各列出方程,求图中道路的宽分别是多少 学生动手尝试解答,教师合理引导两种常用解法,让学生选择自己易接受的方法。 选取教材中的重点题型,进行“回顾式”引入。复习两种常用的解法。
9、(2006年 四川广元)如图,某小区规划在一个长为40米,宽26米的矩形场地ABCD上修建三条相同宽度的甬路,使其中两条与AD平行,另一条与AB平行,其余部分种草,若使每块草坪面积都是144平方米,求道路的宽度。 10、如下图设计方案,长32米,宽20米,各道路的宽度相等,草坪的总面积为540平方米,求道路的宽?11、要设计一幅长为20cm,宽为10cm的图案,其中有两横两竖的彩条,横竖彩条的宽度比为2:1,如果要使剩下面积为152cm2, 应如何设计彩条的宽度?12、提出思考问题。“在矩形中,修多条路时,如何求求路宽的方法?”(备用思考题)如图,某小区计划在一块梯形草地上修建三条宽度相同的小路,该梯形上底16米,下底40米,高26米,在两腰中点连线处有一条横向小路,上下两底之间有两条纵向小路,各小路宽度相等,剩余草地面积为576平方米,小路的宽是多少? 学生再次运用自己喜欢的方法进行解答。学生自主思考,探讨解决问题的方法学生积极尝试,教师引导讲评。学生归纳总结此类题的方法。学生尝试解决,教师启发思路。 此题表面选取于中考题,实际是第8题的变式题,有一定的巩固、提升作用,在复习中取到承前启后的桥梁作用。将方法应用到题中,感受“平移法中的有效性和必要性”,对学生的思维层次进行了必要的提升,感受“平移法”重要作用。此题是上面题的变式题,从“等宽”变形到“不等宽”,可以真正理解平移法的精髓。归纳方法,将解题方法一般化,使学生能够触类旁通,解决此类问题。将矩形问题扩展到等腰梯形。
三、课堂小结
同课章节目录
