人教版数学 七年级上册期末专训:与线段有关的动点问题(含答案)
文档属性
| 名称 | 人教版数学 七年级上册期末专训:与线段有关的动点问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 516.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 19:32:03 | ||
图片预览




文档简介
人教版数学2023-2024学年七年级上册期末专训:
与线段有关的动点问题
1.如图,C是线段上一点,,,点P从A出发,以的速度沿向右运动,终点为B;点Q从点B出发,以的速度沿向左运动,终点为A.已知P、Q同时出发,当其中一点到达终点时,另一点也随之停止运动.设点P运动时间为ts.
(1)当P、Q两点重合时,求t的值;
(2)是否存在某一时刻,使得C、P、Q这三个点中,有一个点恰好是另外两点所连线段的中点?若存在,求出所有满足条件的t值;若不存在,请说明理由.
2.点A在数轴上对应的数为a,点B对应的数为b,且a,b满足|a+2|+(b﹣10)2=0.
(1)求线段AB的长;
(2)线段CD在点A左侧沿数轴向右匀速运动,经过线段AB需要10秒,经过点O的时间是2秒,求CD的长度;
(3)点E在数轴上对应的数为6,点F与点B重合.线段EF以每秒2个单位长度的速度向左运动,同时点P从点A左侧某处以每秒3个单位长度的速度向右运动,点G是线段BE的中点,点P与点E相遇t秒后与点G相遇.若在整个运动过程中,PE=kFG恒成立,求k与t的值.
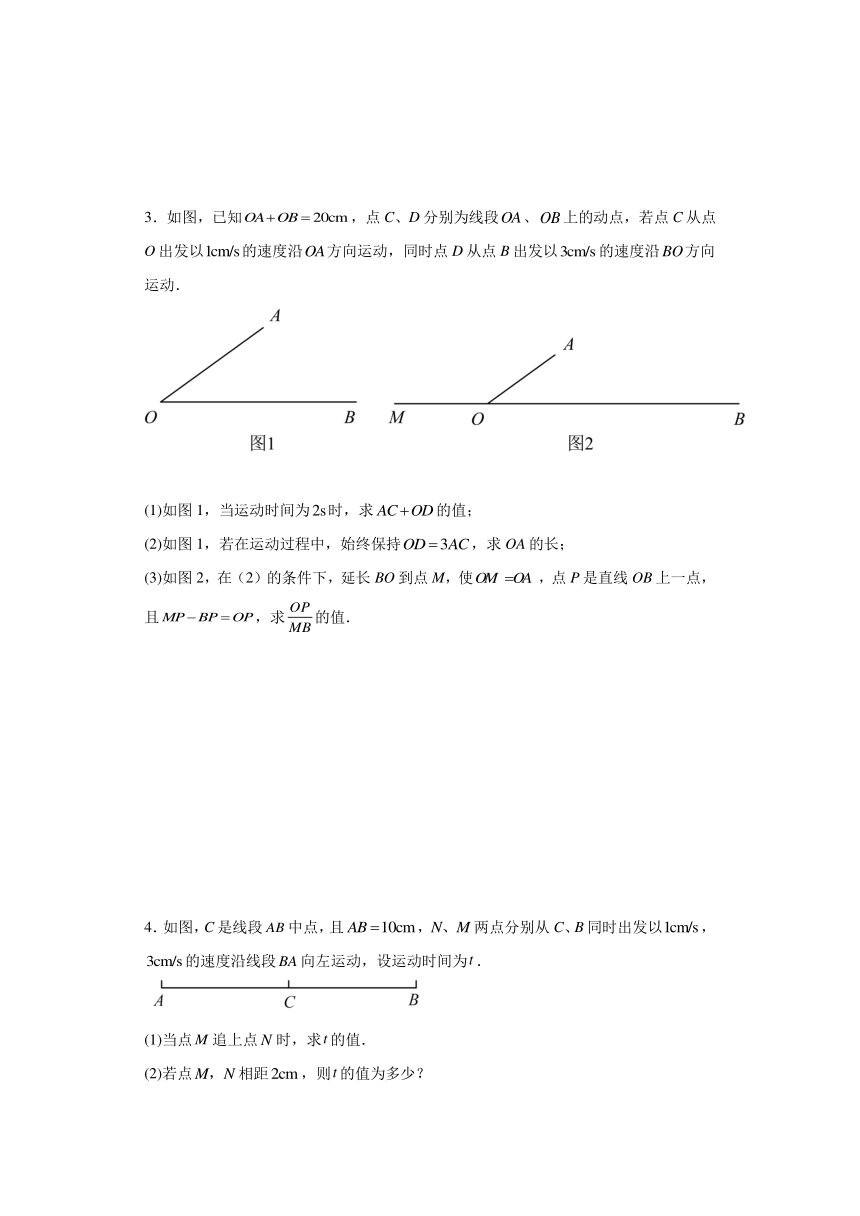
3.如图,已知,点C、D分别为线段、上的动点,若点C从点O出发以的速度沿方向运动,同时点D从点B出发以的速度沿方向运动.
(1)如图1,当运动时间为时,求的值;
(2)如图1,若在运动过程中,始终保持,求OA的长;
(3)如图2,在(2)的条件下,延长BO到点M,使,点P是直线OB上一点,且,求的值.
4.如图,C是线段中点,且,两点分别从C、B同时出发以,的速度沿线段向左运动,设运动时间为.
(1)当点追上点时,求的值.
(2)若点相距,则的值为多少?
5.如图,在数轴上点A表示的数是a,点B表示的数是b,且,
(1)填空: , ;
(2)在线段上有一点C,满足,求点C表示的数;
(3)动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动;动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速移动;动点M从点A出发,以每秒3个单位长度的速度沿数轴向左匀速移动,设运动时间为t秒,当时,的值是否发生变化?若不变求出其值;若变化,写出范围.
6.已知线段AB=12,CD=6,线段CD在直线AB上运动(C、A在B左侧,C在D左侧).
(1)M、N分别是线段AC、BD的中点,若BC=4,求MN;
(2)当CD运动到D点与B点重合时,P是线段AB延长线上一点,下列两个结论:①是定值;
②是定值,请作出正确的选择,并求出其定值.
7.如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,
(1)求线段MN的长.
(2)当C在AB延长线上时,其他条件不变,求线段MN的长.
8.已知,一个点从数轴上的原点开始.先向左移动6cm到达A点,再从A点向右移动10cm到达B点,点C是线段AB的中点.
(1)点C表示的数是 ;
(2)若点A以每秒2cm的速度向左移动,同时C、B两点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①运动t秒时,点C表示的数是 (用含有t的代数式表示);
②当t=2秒时,CB AC的值为 .
③试探索:点A、B、C在运动的过程中,线段CB与AC总有怎样的数量关系?并说明理由.
9.如图,在射线OM上有三点A,B,C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O出发,沿OM方向以1cm/s的速度运动,点Q从点C出发在线段CO上向点O匀速运动(点Q运动到点O时停止运动),两点同时出发.
(1)当PA=2PB(P在线段AB上)时,点Q运动到的位置恰好是线段AB的中点,求点Q的运动速度;
(2)若点Q的运动速度为3cm/s,经过多长时间P,Q两点相距70cm?
(3)当点P运动到线段AB上时,分别取OP和AB的中点E,F,求.
10.线段,点为上的一个动点,点分别是和的中点.
(1)若点恰好是中点,求的长:
(2)若,求的长.
11.如图,已知线段,,线段在直线上运动(点在点的左侧,点在点的左侧),若.
(1)求线段,的长;
(2)若点,分别为线段,的中点,,求线段的长;
(3)当运动到某一时刻时,点与点重合,点是线段的延长线上任意一点,下列两个结论:①是定值,②是定值,请选择你认为正确的一个并加以说明.
12.A,B两地相距a千米,C地在AB的延长线上,且千米,D是A、C两地的中点.
(1)求AD长(结果用含a的代数式表示).
(2)若千米,求a的值.
(3)甲、乙两车分别从A、D两地同时出发,都沿着直线AC匀速去C地,经4小时甲追上乙.当甲追上乙后甲马上原路返回,甲返回行驶1小时时发现甲车距D地50千米,已知千米,求乙车行驶的平均速度
13.点是线段上一点,若(n为大于1的正整数),则我们称点是的最强点.例如,,,则,称E是的最强点;,则是的最强点.
(1)点在线段上,若,,点是的最强点,则 .
(2)若,是的最强点,则 .(用n的代数式表示)
(3)一直线上有两点A,B,,点从B点出发,以每秒的速度向A运动,运动到点A时停止.点D从点A出发,以每秒的速度沿射线运动,t为多少时,点B,,D恰好有一个点是其余2个点的最强点.(用n的代数式表示)
14.如图,点P是定长线段上一点,从点从点B同时出发分别以每秒厘米的速度沿直线向左运动(C在线段上,D在线段上),并满足下列条件:
①关于m、n的单项式与的和仍为单项式;
②在运动过程中,总有.
(1)直接写出:_______,_______;
(2)求出的值,并说明理由:
(3)在运动过程中,分别是的中点,运动t秒时,恰好满足,求此时的值.
15.如图,点C是线段AB上的一点,线段AC=8m,.机器狗P从点A出发,以6m/s的速度向右运动,到达点B后立即以原来的速度返回;机械猫Q从点C出发,以2m/s的速度向右运动,设它们同时出发,运动时间为xs.当机器狗P与机械猫Q第二次相遇时,机器狗和机械猫同时停止运动.
(1)BC=______m,AB=______m;
(2)试通过计算说明:当x为何值时,机器狗P在点A与机械猫Q的中点处?
(3)当x为何值时,机器狗和机械猫之间的距离PQ=2m?请直接写出x的值.
试卷第1页,共3页
参考答案:
1.(1)
(2)存在,满足条件的值为4或7或
2.(1)线段AB的长为12;
(2)CD的长度为3个单位长度;
(3)k的值为5,t的值为1.
3.(1)
(2)
(3)或
4.(1)
(2)或
5.(1)8,
(2)
(3)的值不会发生变化,
6.(1)MN=9;(2)①是定值2.
7.(1)3cm;(2)3cm
8.(1)-1;(2)①﹣1+t;②121;③线段CB与AC相等,
9.(1)点Q的运动速度为cm/s;(2)经过5秒或70秒两点相距70cm;(3).
10.(1)6cm;(2)6cm
11.(1),;(2)9;(3)②正确,,
12.(1)千米;(2)千米;(3)乙车平均速度为50km/h或km/h
13.(1)
(2)
(3)当t为或或或或或时,点B,,D恰好有一个点是其余2个点的最强点
14.(1)1,2
(2)3
(3)
15.(1)16,24.
(2)当x=,即运动秒时,机器狗P在点A与机械猫Q的中点处.
(3)当x=或x=或x=,即运动x=或x=或x=秒时,机器狗和机械猫之间的距离PQ=2m.
答案第1页,共2页
与线段有关的动点问题
1.如图,C是线段上一点,,,点P从A出发,以的速度沿向右运动,终点为B;点Q从点B出发,以的速度沿向左运动,终点为A.已知P、Q同时出发,当其中一点到达终点时,另一点也随之停止运动.设点P运动时间为ts.
(1)当P、Q两点重合时,求t的值;
(2)是否存在某一时刻,使得C、P、Q这三个点中,有一个点恰好是另外两点所连线段的中点?若存在,求出所有满足条件的t值;若不存在,请说明理由.
2.点A在数轴上对应的数为a,点B对应的数为b,且a,b满足|a+2|+(b﹣10)2=0.
(1)求线段AB的长;
(2)线段CD在点A左侧沿数轴向右匀速运动,经过线段AB需要10秒,经过点O的时间是2秒,求CD的长度;
(3)点E在数轴上对应的数为6,点F与点B重合.线段EF以每秒2个单位长度的速度向左运动,同时点P从点A左侧某处以每秒3个单位长度的速度向右运动,点G是线段BE的中点,点P与点E相遇t秒后与点G相遇.若在整个运动过程中,PE=kFG恒成立,求k与t的值.
3.如图,已知,点C、D分别为线段、上的动点,若点C从点O出发以的速度沿方向运动,同时点D从点B出发以的速度沿方向运动.
(1)如图1,当运动时间为时,求的值;
(2)如图1,若在运动过程中,始终保持,求OA的长;
(3)如图2,在(2)的条件下,延长BO到点M,使,点P是直线OB上一点,且,求的值.
4.如图,C是线段中点,且,两点分别从C、B同时出发以,的速度沿线段向左运动,设运动时间为.
(1)当点追上点时,求的值.
(2)若点相距,则的值为多少?
5.如图,在数轴上点A表示的数是a,点B表示的数是b,且,
(1)填空: , ;
(2)在线段上有一点C,满足,求点C表示的数;
(3)动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动;动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速移动;动点M从点A出发,以每秒3个单位长度的速度沿数轴向左匀速移动,设运动时间为t秒,当时,的值是否发生变化?若不变求出其值;若变化,写出范围.
6.已知线段AB=12,CD=6,线段CD在直线AB上运动(C、A在B左侧,C在D左侧).
(1)M、N分别是线段AC、BD的中点,若BC=4,求MN;
(2)当CD运动到D点与B点重合时,P是线段AB延长线上一点,下列两个结论:①是定值;
②是定值,请作出正确的选择,并求出其定值.
7.如图,线段AB上有一任意点C,点M是线段AC的中点,点N是线段BC的中点,当AB=6cm时,
(1)求线段MN的长.
(2)当C在AB延长线上时,其他条件不变,求线段MN的长.
8.已知,一个点从数轴上的原点开始.先向左移动6cm到达A点,再从A点向右移动10cm到达B点,点C是线段AB的中点.
(1)点C表示的数是 ;
(2)若点A以每秒2cm的速度向左移动,同时C、B两点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①运动t秒时,点C表示的数是 (用含有t的代数式表示);
②当t=2秒时,CB AC的值为 .
③试探索:点A、B、C在运动的过程中,线段CB与AC总有怎样的数量关系?并说明理由.
9.如图,在射线OM上有三点A,B,C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O出发,沿OM方向以1cm/s的速度运动,点Q从点C出发在线段CO上向点O匀速运动(点Q运动到点O时停止运动),两点同时出发.
(1)当PA=2PB(P在线段AB上)时,点Q运动到的位置恰好是线段AB的中点,求点Q的运动速度;
(2)若点Q的运动速度为3cm/s,经过多长时间P,Q两点相距70cm?
(3)当点P运动到线段AB上时,分别取OP和AB的中点E,F,求.
10.线段,点为上的一个动点,点分别是和的中点.
(1)若点恰好是中点,求的长:
(2)若,求的长.
11.如图,已知线段,,线段在直线上运动(点在点的左侧,点在点的左侧),若.
(1)求线段,的长;
(2)若点,分别为线段,的中点,,求线段的长;
(3)当运动到某一时刻时,点与点重合,点是线段的延长线上任意一点,下列两个结论:①是定值,②是定值,请选择你认为正确的一个并加以说明.
12.A,B两地相距a千米,C地在AB的延长线上,且千米,D是A、C两地的中点.
(1)求AD长(结果用含a的代数式表示).
(2)若千米,求a的值.
(3)甲、乙两车分别从A、D两地同时出发,都沿着直线AC匀速去C地,经4小时甲追上乙.当甲追上乙后甲马上原路返回,甲返回行驶1小时时发现甲车距D地50千米,已知千米,求乙车行驶的平均速度
13.点是线段上一点,若(n为大于1的正整数),则我们称点是的最强点.例如,,,则,称E是的最强点;,则是的最强点.
(1)点在线段上,若,,点是的最强点,则 .
(2)若,是的最强点,则 .(用n的代数式表示)
(3)一直线上有两点A,B,,点从B点出发,以每秒的速度向A运动,运动到点A时停止.点D从点A出发,以每秒的速度沿射线运动,t为多少时,点B,,D恰好有一个点是其余2个点的最强点.(用n的代数式表示)
14.如图,点P是定长线段上一点,从点从点B同时出发分别以每秒厘米的速度沿直线向左运动(C在线段上,D在线段上),并满足下列条件:
①关于m、n的单项式与的和仍为单项式;
②在运动过程中,总有.
(1)直接写出:_______,_______;
(2)求出的值,并说明理由:
(3)在运动过程中,分别是的中点,运动t秒时,恰好满足,求此时的值.
15.如图,点C是线段AB上的一点,线段AC=8m,.机器狗P从点A出发,以6m/s的速度向右运动,到达点B后立即以原来的速度返回;机械猫Q从点C出发,以2m/s的速度向右运动,设它们同时出发,运动时间为xs.当机器狗P与机械猫Q第二次相遇时,机器狗和机械猫同时停止运动.
(1)BC=______m,AB=______m;
(2)试通过计算说明:当x为何值时,机器狗P在点A与机械猫Q的中点处?
(3)当x为何值时,机器狗和机械猫之间的距离PQ=2m?请直接写出x的值.
试卷第1页,共3页
参考答案:
1.(1)
(2)存在,满足条件的值为4或7或
2.(1)线段AB的长为12;
(2)CD的长度为3个单位长度;
(3)k的值为5,t的值为1.
3.(1)
(2)
(3)或
4.(1)
(2)或
5.(1)8,
(2)
(3)的值不会发生变化,
6.(1)MN=9;(2)①是定值2.
7.(1)3cm;(2)3cm
8.(1)-1;(2)①﹣1+t;②121;③线段CB与AC相等,
9.(1)点Q的运动速度为cm/s;(2)经过5秒或70秒两点相距70cm;(3).
10.(1)6cm;(2)6cm
11.(1),;(2)9;(3)②正确,,
12.(1)千米;(2)千米;(3)乙车平均速度为50km/h或km/h
13.(1)
(2)
(3)当t为或或或或或时,点B,,D恰好有一个点是其余2个点的最强点
14.(1)1,2
(2)3
(3)
15.(1)16,24.
(2)当x=,即运动秒时,机器狗P在点A与机械猫Q的中点处.
(3)当x=或x=或x=,即运动x=或x=或x=秒时,机器狗和机械猫之间的距离PQ=2m.
答案第1页,共2页
